数列在购房贷款中的应用

黄映丽

（广东省梅县东山中学 广东梅州 514000）

一、问题的背景

数学家华罗庚曾说过：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，日月之繁，无处不用数学。”这是对生活与数学关系的精彩描述。

当今，随着人们生活水平的提高，大家的消费观念也发生了转变，分期付款、贷款购物已深入我们的生活中，不再生疏，分期付款方式在今天的商业活动中应用日趋广泛，可以贷款买房，贷款买车，贷款创业；助学贷款，旅游贷款，甚至还可以贷款买手机、电视、电脑等小物件。可见，贷款已经是一种相当普遍的生活方式了。那么对于贷款的利息、还贷期限、还款金额等又是如何计算的？课本例题：某人2004年初银行申请个人住房商业贷款20万元购买住房，月利率为3.375‰，按复利计算利，每月等额还贷一次，并从贷款后的次月初开始还贷，如果10年还清，那么每个月应还贷多少钱？

二、问题的提出

从课本这道例题出发，让学生自己去银行了解目前买房商业贷款还贷利率是多少？还贷方式最常用的方式有几种？哪种还贷方法比较省钱？

三、探究、解决方案

学生从银行了解到在生活中应用较多的分期付款还贷的模式基本有两种：一种是等额本息还款，即按月等额归还贷款本息的方法。一种是等额本金还款，即将本金分别摊派到每个月内，同时，付清上一个交易日至本次还款日之间的利息。

1.个人住房“等额本息”还款法

该类分期付款问题规定：

（1）一般按每（月）一期等额付款，即等额本息还款，合同签订后，不得更改；

（2）每期利息按复利计算，即上期利息要记入下期本金。注意：分期付款中，贷款与每期付款额在贷款付清前，均会随着时间的推移不断增值，时间愈长，利息愈多，增值愈大。

一般地，设本金（即贷款额）为A万元，月利率为r，约定n个月将贷款还清，月均还款额为B，则有

根据中国人民银行规定：贷款在1年以内的，到期本息一次性清偿还款，其他期限按下表执行：商业性个人住房等额本息还款表：

?

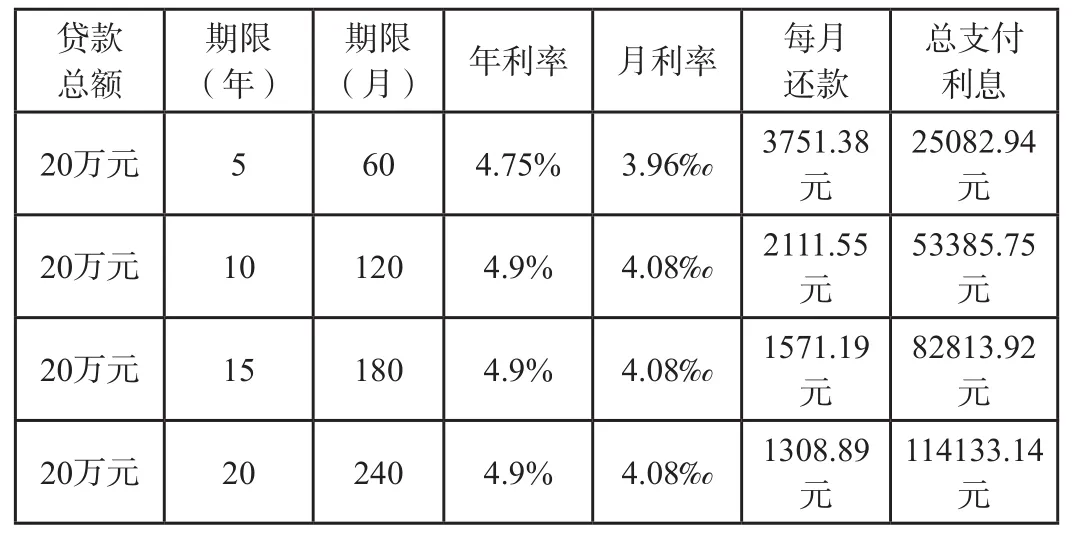
2.个人住房“等额本金”还款法

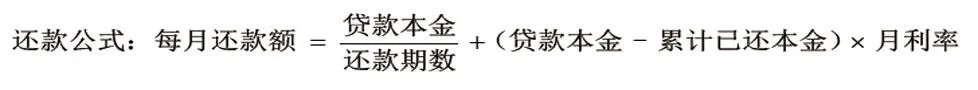
学生根据调查了解到的情况，绘制的上表，结合现实当中购房家庭的实际情况：存款、月收入、压力等方面情况进行了激烈的讨论，提出了不同的解决方案。见商业性个人住房等额本金还款表

四、课后反思

本节课首先从贷款问题入手，从学生的生活实践中提取问题背景，使问题更生活化，充分调动学生参与、探求的学习欲望。在例题中先理解“复利计息法”，将实际问题数学化，采用数列建模，通过逐年计算还款数来理解，这是学生容易接受的，数学具有“从具体情境上升为一般的概念和结论，又从一般返回到具体情形加以印证和应用”的特性。

通过本节课的学习，使学生能够了解银行还款中的有关知识，能够应用数学模型解决还款中的有关问题，提高学生解决问题能力，同时，让学生参与数学建模过程，应用模型解决实际问题，通过对方法的总结、归纳，让学生感知、体验模型思想的过程，从中感受生活中的数学模型，领会数学知识的运用。使学生在解决问题的过程中得到用数学、学数学的实际体验，加深对知识的掌握和理解，感受到生活中处处都有数学，离不开数学，加强学生对数学学习的自信心。

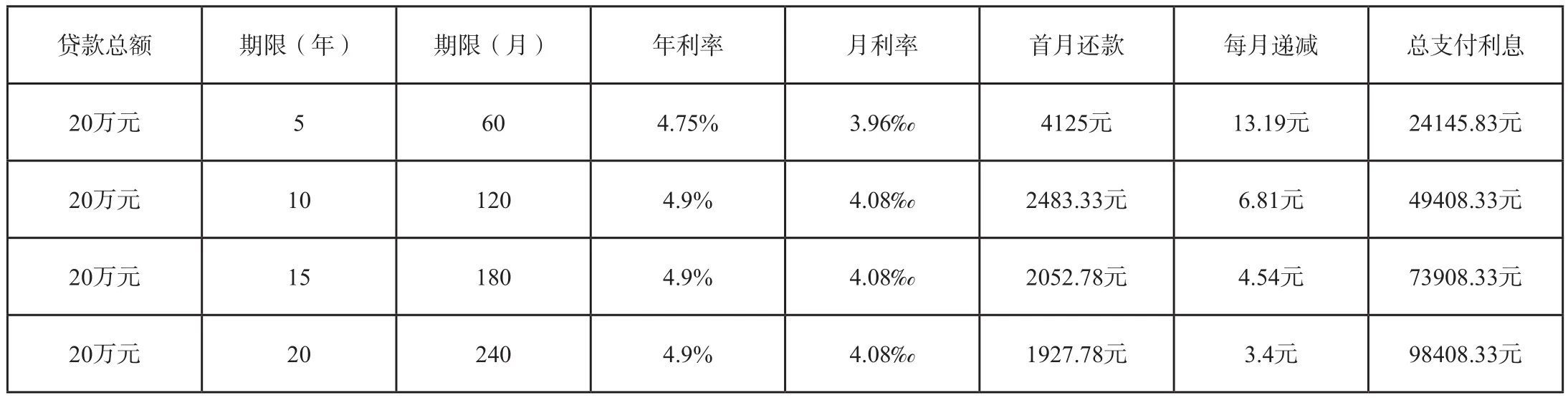
商业性个人住房等额本金还款表