考虑岩体损伤的爆破振动速度衰减多元非线性模型*

张勤彬，程贵海，卢欣奇，徐中慧，董海佩

(1.广西大学 资源环境与材料学院， 广西 南宁 530004；2. 西南科技大学 环境与资源学院，四川 绵阳 621000)

0　引言

爆破作为一种有效的施工手段，在中国被广泛应用于矿业、土建、交通及水利水电等工程领域，是大规模岩土开挖的主要施工手段。但是，在爆破施工过程中，爆破引起的振动效应可能会对爆区周围的建、构筑物造成影响，甚至是破坏。爆破振动受不同因素的影响，主要包括爆区环境、岩体的力学性质、爆破最大段药量、微差时间、传播距离等[1-2]。由于这些因素与爆破振动的传播规律之间存在着极其复杂的非线性关系，加上相关理论研究的不足，导致采用传统经验公式不能准确的预测爆破振动的传播规律。因此，分析及改进传统经验公式的不足，提高预测爆破振动速度经验公式的精度，控制爆破振动的影响，就成为工程爆破研究的主要内容之一[3]。

近年来，爆破振动衰减规律的预测研究工作取得了很大突破。传统的爆破振动研究方法，常用工程中得到的监测数据，根据萨道夫斯基公式进行回归分析，然后得到萨道夫斯基公式的相关参数K,α的值：

(1)

式中：K为与岩石性质、爆破参数和爆破方法有关的场地系数；Q为爆破最大段药量，kg；R为爆源距，即爆源中心与测点的直线距离，m；α为爆破振动衰减系数。

许多工程实践表明，采用萨道夫斯基公式预测周围质点的爆破振动速度，在平整的地形条件下的精确度较高，在预测地形地貌变化较大的质点振动峰值速度时，其精确度大大降低。因此，后续的研究相继引入了高程差对爆破振动峰值速度的影响，周同龄等[4]通过研究表明：高差为正，爆破所产生的振动效应增大。质点振动速度由以下公式表征：

(2)

式中:H为测点与爆源之间的高程差，m；L为测点与爆源之间的水平距离，m；β为与高程差有关的系数。但该公式未全面考虑高程差对振动速度的影响。王在泉等[5]通过研究得出：爆破振动的放大效应，不一定是单调递增的，通过实际工程验证，提出质点振动速度公式由下式表征：

(3)

唐海等[6]在式(3)的基础上，引入了地貌因素对爆破振动峰值速度的影响，通过无量纲处理后，得出表征质点振动速度的公式为：

(4)

式中：K为场地系数;K2为地貌影响因素;α为衰减系数;β为高程差影响因素;其他符号意义与之前公式相同。

通过研究发现，爆破振动影响因素的主要研究对象为：最大同段药量Q,爆源距R,高程差H，水平距离L。在国内，爆区周围的岩体性质对爆破振动的影响大多停留在理论研究阶段，一般情况下用场地系数K表征岩石的力学性质对爆破振动的影响，这类方法未考虑岩石力学性质的动态变化，而对于大多数岩土开挖工程，爆破作业常常是周期性的，受周期性的爆破荷载作用，周围岩体受到不同程度的损伤[7]。如何表征岩体的损伤则成为一个难题，马建军[8]提出了用岩体弹性模量的变化来表示岩体的损伤，岩体的损伤量用下式表示：

(5)

式中：E为爆破后岩体的弹性模量,E0为爆破前岩体的弹性模量。

然而，国内对于岩体累计损伤情况下，爆破振动衰减规律的研究仅停留在定性阶段。文章首次通过研究爆破作用下岩体的损伤及裂隙直径对爆破振动的影响，通过无量纲分析，得出了爆破振动在岩石累计损伤下的预测公式，并通过实际工程进行了相关验证。

1　爆破振动经验公式的分析

在爆炸荷载的作用下，向外传播的压应力作用于岩体，形成压碎区空腔、并产生径向裂隙。随着爆生气体压力的释放，岩体内部积蓄的弹性变形将迅速释放，向爆源中心产生拉应力。由于岩石的抗拉强度远远低于岩石的抗压强度，当产生的拉应力大于岩石本身的抗拉强度时，则在岩体粉碎区外形成裂隙区，其切向峰值拉应力与距离的关系为[9]：

(6)

式中：σθmax为切向峰值拉应力；λ为侧压系数，λ=μ/(1-μ)，μ为泊松比；Pd爆炸冲击波初始冲击压力；r0=RL/rb，RL为裂隙圈半径，rb为炮孔半径;α为应力波衰减指数,与爆破振动衰减指数不同，α=2-μ/(1-μ)。

岩石所承受的冲击波和应力波作用的应力大小与岩体的声阻抗成正比，故冲击波的初始压力为[10]：

(7)

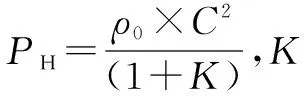
可用岩石抗拉强度ST代替σθmax，得裂隙圈半径为[12]：

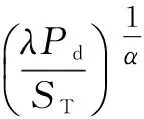
(8)

爆破振动的速度V主要和爆破最大段装药量Q，距离爆源的直线距离R，距离爆源的高程差H，岩体的密度ρ，振动波的传播速度c，爆轰时间t，岩体损伤量D及裂隙圈半径RL有关。可以表示为[6]:

V=φ(Q,R,H,ρ,c,t,D,RL)

(9)

假设θ为无量纲参量,Q，R和c为独立量纲，则

(10)

其中ω，ξ，δ为待定参数。定义V为：

V=LT-1=(M)ω(R)ξ(c)δ

(11)

当ω= 0，ξ=0，δ=1时，式(11)成立。同理可以得出[13]：

(12)

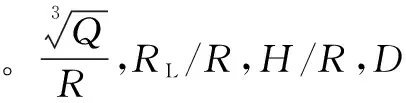
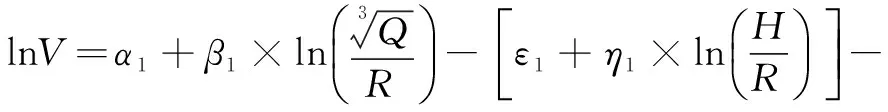
(13)

假设V0满足:

(14)

假设lnK1=α1，可以得到：

(15)

所得式(15)就为平整地形条件下的萨道夫斯基公式，与式(1)相同。则lnV可以写成：

(16)

(17)

假设lnK2=-ε1，β2=-η1，D×β3=φ，则在岩石损伤条件下，爆破引起的质点峰值振动速度计算公式为：

(18)

式中：K1是场地系数；K2是地形影响系数；β1是衰减系数；β2是高程影响系数；β3是岩石损伤影响系数；D是岩体损伤系数。

2　工程实例分析

2.1　工程概况

该工程位于西南地区，是一个露天石英矿山，岩石中等硬度，f=6～9，裂隙发育一般，该段矿层倾角平均为25～40°。开采台阶高度10 m，爆区为山坡地形，爆区岩体的相关参数见表2，400 m以外为居民区，已经累计进行爆破作业9次，本文对第8次及第9次的爆破振动进行了监测、分析。仪器采用TC-4850爆破测振仪对爆破振动进行监测，如图1所示。

图1　3号测点安装示意Fig.1　The layout of the 3# measurement point

工程采用台阶爆破，炮孔直径120 mm，排距2.5 m，孔距4.5 m，采用梅花形(三角形)布置炮孔，第8次爆破总装药量4 700 kg，同段最大药量1 210 kg；第9次爆破总装药量3 800 kg，同段最大药量1 100 kg。炸药密度ρ0为1 240 kg/m3，炸药爆速为4 200 m/s，炸药其他相关参数见表1。在居民区共布置8个监测点，爆区环境及测点布置情况如图2所示。

表1　炸药相关参数

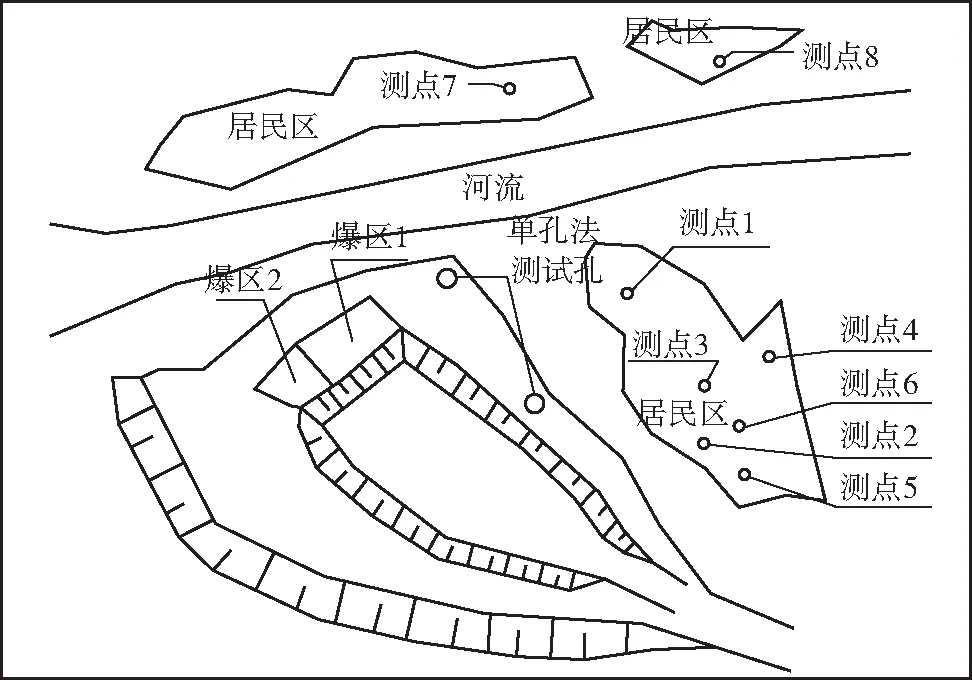
图2　爆区环境及测点布置Fig.2　Surroundings of blast zone and measurement points

由于岩体的弹性模量很难直接测得，但可采用单孔波速测试法测得纵波传播速度[14]；岩体的弹性模量可依据公式(19)由纵波传播速度进行反推得出岩体的平均弹性模量，由于篇幅限制，单孔波速测试原理在此不做叙述[15]。

(19)

式中：E为弹性模量；Vp为纵波波速；ρ为矿岩密度；μ为泊松比。根据其工程地质勘查报告，岩体初始弹性模量为4.672 4×104～6.152 2×104MPa，采用单孔波速测试法得出爆破前、第8次及第9次爆破后岩体的平均纵波传播速度分别为4 922，4 206，3 999 m/s。根据式(19)得出初始岩体弹性模量为 5.642 3×104MPa，2次爆破后的弹性模量分别为4.119 5×104，3.724 5×104MPa，矿岩密度ρs为2 700 kg/m3，岩体其他力学性能见表2。

表2　岩体相关参数

2.2　监测结果

爆破振动的测试是在该石英露天矿第8次和第9次爆破作业时进行的，根据表2相关数据，通过式(5)计算，得第8次爆破作业后岩体累计损伤度D1为0.27，第9次爆破作业后岩体的累计损伤度D2为0.34。2次爆破时8个测点的峰值振动速度如表3所示。

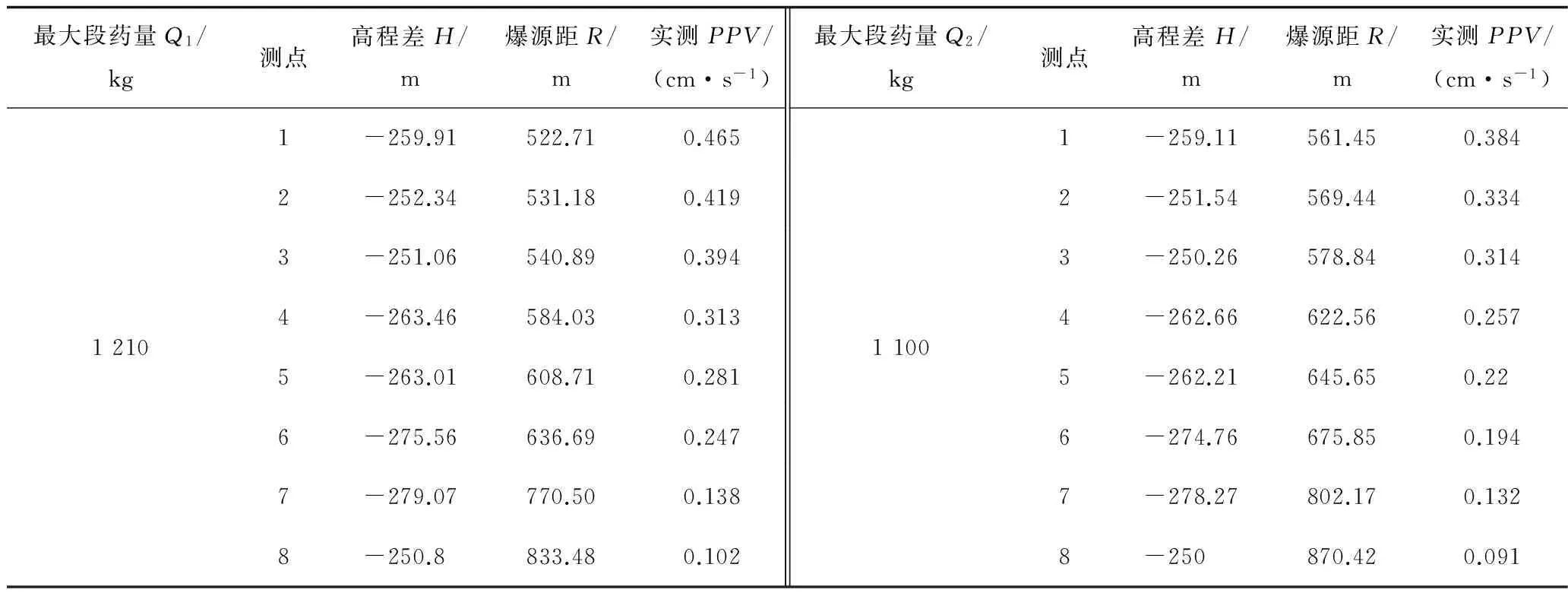
表3　各测点的峰值振动速度

注：实测PPV为3个分量中的最大值

3　爆破振动衰减规律

3.1爆破振动峰值速度衰减规律

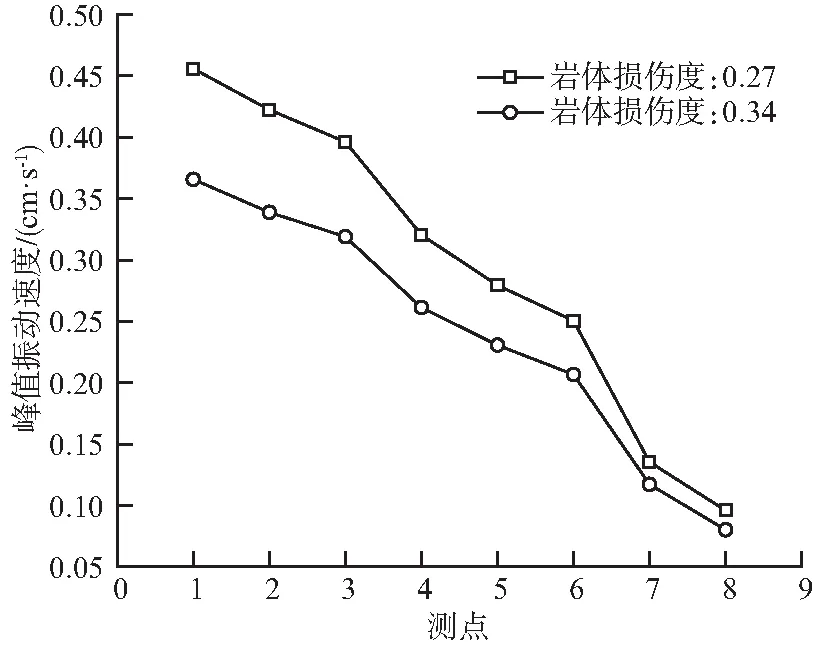
图3　不同岩体损伤度下对应的PPVFig.3　Measured PPV for different rock masses damage degree

工程中常用监测质点的峰值振动速度来表征爆破作业所产生的振动强度大小，根据表3所得数据，通过对比分析8个测点2次不同的监测结果，得到了石英矿岩体不同累计损伤度与爆破振动峰值速度的关系曲线，如图3所示。

从图3可以看出，不同岩体累计损伤度所对应的爆破振动峰值速度不同，累计损伤度越大，爆破振动峰值速度越小，岩体的损伤对爆破振动的传播起到了衰减作用，根据2条线的斜率可以看出，损伤度越大，其衰减速度越快。

3.2　回归分析

首先分析不考虑岩体累计损伤的情况，表4分别是根据式1～4建立非线性回归模型，所得到的各参数的值，表5是对应2次爆破作业的爆破振动峰值速度的预测值。

表4　不同方程回归得到的参数值

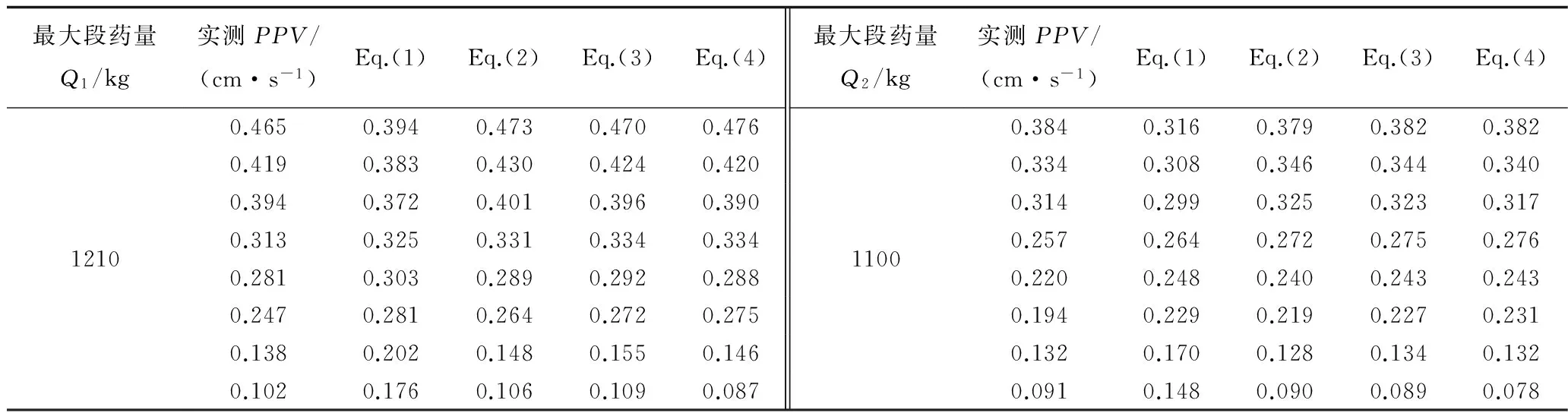
表5　不同方程回归得到的PPV预测值

图4，图5分别为第8次、第9次爆破作业的PPV预测值曲线。从图中结果可以看出在不考虑岩体损伤的情况下，采用经验公式预测出的爆破振动峰值速度普遍大于实测值，未能较好的反应出爆破振动的衰减规律，式(1)相对实测值的平均偏差为20.537%，式(2)的相对平均偏差为5.593%，式(3)的相对平均偏差为5.441%，式(4)的相对平均偏差为6.251%。

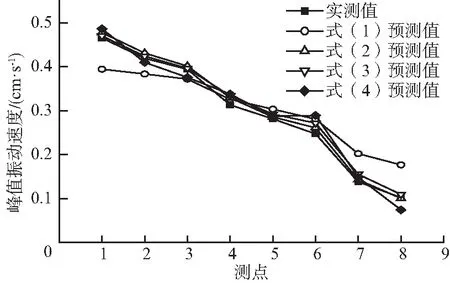
图4　第8次爆破作业的PPV预测值Fig.4　Predicted PPV of 8th blasting

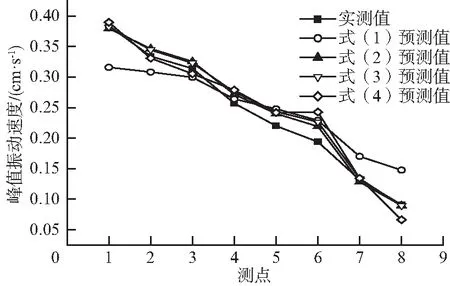
图5　第9次爆破作业的PPV预测值Fig.5　Predicted PPV of 9th blasting

Parameterk1,k2,β1,β2,β3;

VariableV,R,H;

!Fixedparameters:Q，RL，D

FunctionV=k1×k2×(Q1/3/R)^β1×(H/R)^c×(RL/R)^(D×d);

Data(V，Q，R，H，RL，D);

采用多元非线性回归的分析方法，得出了不同测点爆破振动速度的拟合值见表6。

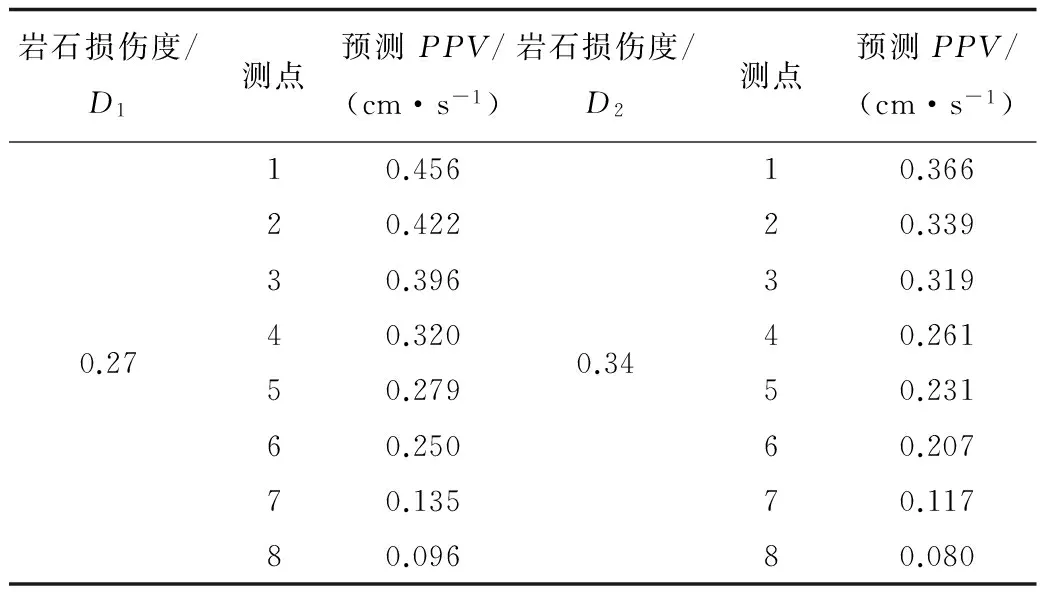
表6　式(18)的PPV预测值

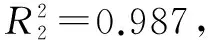
图6，图7分别是损伤度为0.27，0.34时，不同测点实测的峰值振动速度及多元非线性拟合值的关系。

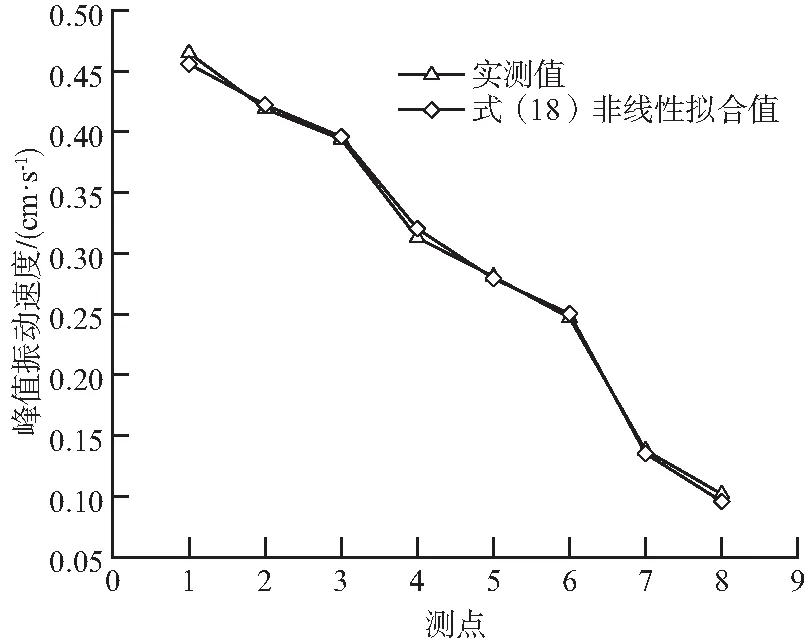
图6　岩石损伤度为0.27Fig.6　Damage degree of rock masses is 0.27

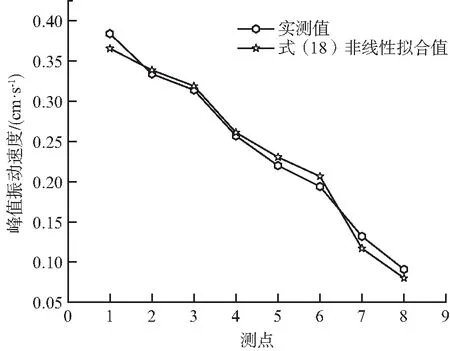
图7　岩石损伤度为0.34Fig.7　Damage degree of rock masses is 0.34

通过对比可以看出，采用式(18)进行多元非线性回归得到的质点峰值振动速度与实测值更接近，但是在累计损伤度增大的情况下，其预测精度将会有所降低，当累计损伤度为0.27时，采用该经验公式预测的平均偏差为1.950%，当累计损伤度为0.34时，其平均偏差为5.490%，预测数据与实测数据吻合度较高。

4　结论

1)在我国《爆破安全规程》中，考虑了最大段药量、爆心距、爆破区域地质条件对爆破振动的影响，但很少关注岩体的损伤对爆破振动的影响，少数研究仅仅停留在定性描述阶段，而未进行定量分析，对于需要多次爆破作业的工程来讲，不考虑岩体的累计损伤来预测爆破振动大小是不完善的。

2)考虑岩体损伤受多种因素影响，可以采用岩体弹性模量的变化及爆破裂隙圈半径作为衡量岩体损伤的程度，通过量纲分析可以得出影响爆破振动速度的几个典型因素及其与爆破振动速度之间的解析关系。

3)用传统的萨道夫斯基公式或其他不合理考虑岩体损伤的经验公式预测工程爆破的振动峰值速度，其精确度不高，预测值普遍大于实测值，不能较好的反应爆破振动的衰减规律，引入岩体损伤度是必要的。

4)对于该工程而言，其监测结果较好的验证了本文所提出的爆破振动经验公式，其误差分别为1.950%，5.490%，均在可接受范围内，但根据结果，随着岩体累计损伤度的增大，式(18)的预测精度也有所降低。

5)爆破振动的衰减正是岩体内部损伤的外在表现，岩体的累计损伤对爆破所产生的振动速度具有较好的衰减作用，实际工程中，可采用预裂法隔断爆区与被保护建筑，或开挖一定深度的减振沟，可以大大减小爆破地震效应。

[1]吕涛, 石永强, 黄诚,等. 非线性回归法求解爆破振动速度衰减公式参数[J]. 岩土力学, 2007, 28(9): 1871-1878.

LYU Tao, SHI Yongqiang, HUANG Cheng, et al. Study on attenuation parameters of blasting vibration by nonlinear regression analysis[J]. Rock & Soil Mechanics, 2007, 28(9):1871-1878.

[2]陶铁军, 池恩安, 赵明生, 等. 露天铁矿分区爆破振动监测与安全分析[J]. 中国安全生产科学技术, 2012, 8(12): 179-183.

TAO Tiejun, CHI Enan, ZHAO Mingsheng, et al. Monitoring and safety analysis of division blast-induced vibration for open pit iron mine[J]. Journal of Safety Science and Technology, 2012, 8(12): 179-183.

[3]胡建华, 尚俊龙, 罗先伟,等. 单孔爆破振动监测与衰减规律多元线性化回归[J]. 振动与冲击, 2013, 32(16): 49-53.

HU Jianhua, SHANG Junlong, LUO Xianwei, et al. Monitoring of single-hole blasting vibration and detection of its attenuation law by using multiple linear regression[J]. Journal of Vibration & Shock, 2013, 32(16):49-53.

[4]周同岭, 杨秀甫, 翁家杰. 爆破地震高程效应的实验研究[J]. 建井技术, 1997(a12): 31-35.

ZHOU Tongling, YANG Xiufu, WENG Jiajie. Experimental study on elevation effect of blasting vibration. Mine Construction Technology. 1997(a12):31-35.

[5]王在泉, 陆文兴. 高边坡爆破开挖震动传播规律及质量控制[J]. 爆破, 1994(3): 1-4.

WANG Zaiquan, LU Wenxing. Vibration propagation law and quality control of High Slope Blasting Excavation[J]. Blasting,1994(3):1-4.

[6]唐海, 李海波. 反映高程放大效应的爆破振动公式研究[J]. 岩土力学, 2011, 32(3): 820-824.

TANG Hai, LI Haibo. Study of blasting vibration formula of reflecting amplification effect on elevation[J]. Rock and Soil Mech, 2011, 32(3): 820-824.

[7]KUMAR R, CHOUDHURY D, BHARGAVA K. Determination of blast-induced ground vibration equations for rocks using mechanical and geological properties[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(3): 341-349.

[8]马建军. 岩石爆破的相对损伤与损伤累积计算[J]. 岩土力学, 2006, 27(6): 961-964.

MA Jianjun. Relative damage and computation of damage cumulation for blasting in rock[J]. Rock & Soil Mechanics, 2006, 27(6):961-964.

[9]费鸿禄, 洪陈超. 应力波和爆生气体共同作用下裂隙区范围研究[J]. 爆破, 2017, 34(1): 33-36.

FEI Honglu, HONG Chenchao. Study on Crushed and Fracture Zone Range under Combined Action of Stress and Detonation Gas[J]. Blasting, 2017,34(1):33-36.

[10]张志呈. 定向断裂控制爆破[M]. 重庆： 重庆出版社, 2000.

[11]杨伟林, 杨柏坡. 爆破地震动效应的数值模拟分析[J]. 地震工程与工程振动, 2005, 25(1): 8-13.

YANG Weilin, YANG Baipo. Numerical analysis of explosion seismic effect[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(1): 8-13.

[12]张立. 岩石松动爆破裂隙区参数分析与应用[J]. 煤矿爆破, 2011(4): 26-28.

ZHANG Li.Analysis on Parameters of Loosen Blasting Crack Zone and Application[J]. Coal Mine Blasting, 2011(4): 26-28.

[13]程康, 沈伟, 陈庄明,等. 工程爆破引起的振动速度计算经验公式及应用条件探讨[J]. 振动与冲击, 2011, 30(6): 127-129.

CHENG Kang, SHEN Wei, CHEN Zhuangming, et al. Inquiry into calculation formula for vibration velocity induced by engineering blasting and its application conditions[J]. Journal of Vibration & Shock, 2011, 30(6): 127-129.

[14]陈赞成,余斌,解联库,等.大型地下铁矿工程地质调查与岩体质量评价[J].中国安全生产科学技术,2013,9(6):63-68.

CHEN Zancheng, YU Bin, XIE Lianku, et al. Engineering geological investigation and evaluation of rock mass quality in large underground iron mine[J]. Journal of Safety Science and Technology, 2013, 9(6): 63-68.

[15]闫长斌, 徐国元, 杨飞. 爆破动荷载作用下围岩累积损伤效应声波测试研究[J]. 岩土工程学报, 2007, 29(1): 88-93.

YAN Changbin, XU Guoyuan, YANG Fei. Measurement of sound waves to study cumulative damage effect on surrounding rock under blasting load[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(1): 88-93.

[16]饶运章, 汪弘. 爆破振动速度衰减规律的多元线性回归分析[J]. 金属矿山, 2013, 42(12): 46-47.

RAO Yunzhang, WANG Hong. Multiple Regression Linear Analysis on Attenuation Formula of Blasting Vibration Velocity[J]. Metal Mine, 2013, 42(12): 46-47.