基于传递熵与KELM的炼油化工过程风险传播路径分析方法*

蔡　爽，胡瑾秋，张来斌

(中国石油大学(北京) 机械与储运工程学院，油气资源与探测国家重点实验室，北京 102249)

0　引言

炼油化工生产过程复杂，工艺条件苛刻，常伴有高温、高压、低温、真空、大流量、高转速等极端条件，在一个炼油厂区中，一旦某单一设备或工艺过程出现故障，易借助系统单元之间的相互依存、相互制约关系，触发连锁效应，由一种扰动或故障经过一段时间传播，从一个空间传播至另一个更广阔的空间，引起衍生事故，带来难以估量的社会与环境风险，引发出一系列故障链直至引起事故或灾难。为了有效抑制炼油化工过程风险传播，保证生产安全及产品质量，有必要对风险扰动传播路径进行分析研究。现有传播路径分析方法主要是对于故障根原因的分析，以期降低事故后果。而根原因分析的基础在于因果图的建立，主要分为基于过程知识的建模和基于过程数据的建模2大类。基于过程知识的因果性建模方法包括多层流模型(Multilevel Flow Model，MFM)[1]、因果模型(Cause-Effect Model，CE)[2]和符号有向图(Signed Directed Graph，SDG)[3]等。与多层流模型与CE模型相比，符号有向图在复杂的化工过程仿真及实际过程中得到了更为广泛的应用[4-8]。知识建模方法对过程变量间的因果关系进行简单和图形化的描述，易于理解和应用；但该类方法过于依赖专家经验，无法定量描述变量间关联性的大小。基于过程数据的建模方法主要有互相关函数(Ross-correlation function，CCF)、传递熵和贝叶斯网络模型(Bayesian Network，BN)等。互相关函数[9]通过计算2过程变量间的时滞和关联系数，确定2变量的关联程度及传播方向[9-10]。但互相关函数会产生一些冗余时滞干扰分析结果且仅能分析变量间的线性相关关系。文献[11]提出基于解析结构模型的信息融合方法，通过构建连接矩阵和可达矩阵建立相应的因果网络。贝叶斯网络模型[12]可以反映真实过程的随机性和不确定性，但其概率的设置常依据主观经验，且概率的物理意义并不直接。传递熵方法是在信息熵的基础上于2000年被提出的，这是1种基于概率分布、信息熵及统计方法得出时间序列间因果性的方法，可用于分析变量间的非线性相关关系。文献[10,11,13]通过计算2变量间的传递熵，分析过程变量间由于信息传递所带来的因果性。但有时由该数据驱动方法建立的扰动传播路径可能与实际过程不符，有必要结合过程知识检验传播路径的合理性。

因现有方法多是针对故障根原因的诊断，忽视了对风险传播过程的预测及预防，本文提出一种基于传递熵与核极限学习机(Kernel Extreme Learning Machine，KELM)的炼油化工过程风险传播路径分析方法，针对某一工艺扰动分析风险传播过程，基于传递熵分析不同过程变量间的非线性关联关系及传播方向，建立炼油化工过程风险传播推绎模型，并提出一种基于KELM的风险传播搜索方法，预测未来一段时间内风险的可能传播路径，以便操作人员及时切断风险传播路径，保证炼油化工过程生产安全及产品质量。

1　基本原理

传递熵方法是一种基于概率分布、信息熵及统计方法得出时间序列间因果性的方法，可用于分析炼油化工过程监控变量间的非线性相关关系及两变量间信息传递的方向。核极限学习机方法可用于实现炼油化工过程监控变量的时间序列预测，是一种具有较强泛化能力及稳定性的预测方法。下面分别对2种方法的基本原理作一简单介绍。

1.1　传递熵

信息熵是信息论中用于度量信息量的一个概念，其定义为

(1)

式中：p(x)表示变量x的概率分布；Hx表示变量x的信息熵。

2个变量x和y的信息熵大小可用联合熵Hxy表示，其定义为

(2)

式中：p(x,y)为x和y的联合概率分布。

互信息[14]是信息论中用于表示信息之间相关性的一个概念，反映一个随机变量中包含的关于另一个随机变量的信息量，2个变量x和y的互信息Ixy如式(3)：

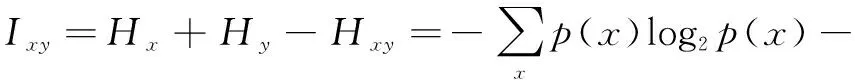
(3)

式中：p(x)和p(y)分别表示变量x和y的概率分布，p(x,y)为x和y的联合概率分布。

但互信息仅能表示两变量间关联性的大小，而无法体现两变量间信息传递的方向。为准确度量动态过程中随机变量之间的关联性及传播方向，T. Schreiber于2000年在信息熵的基础上提出了传递熵分析法[15]，这是一种基于概率分布、信息熵及统计方法得出时间序列间因果性的方法。因传递熵的计算需要长度较大的时间序列，对于过去普遍数据量较小的时代，其应用领域十分受限。随着自动化水平的不断提高，各种传感器被大量应用于炼油化工过程，可被挖掘的数据量和信息也随之增大，使得传递熵在炼油化工过程中的应用成为可能。

变量y到变量x的传递熵定义如式(4)：

(4)

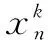
y到x的传递熵实质为y的信息对于x不确定性大小的改变，即y传递给x的信息量的大小。传递熵可作为衡量变量间因果性的指标。由于传递熵考虑的是变量间的信息量传递，而不需要假定变量间具有特定形式的关系，因此具有比Wiener-Granger因果性更好的适用性，尤其是对于具有非线性特征的炼油化工过程变量。

1.2　核极限学习机

极限学习机(Extreme Learning Machine，ELM)[16]是一种单隐层前馈神经网络学习算法。传统的神经网络学习算法(如BP算法)需要人为设置大量的网络训练参数且容易产生局部最优解，而极限学习机只需设置网络的隐层节点个数，在算法执行过程中不需要调整网络的输入权值及隐层神经元的偏置，并且产生唯一的最优解，因此具有学习速度快且泛化性能好的优点。

极限学习机网络训练模型如图1所示：

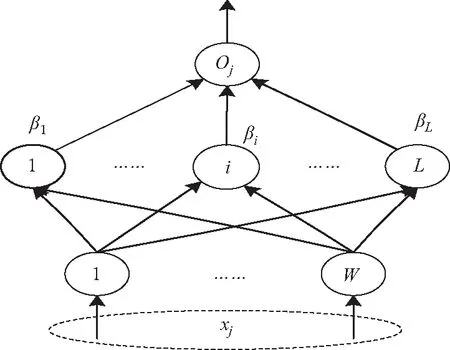
图1　极限学习机网络模型Fig.1　ELM model

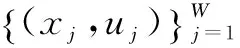
(5)

式中：ωi=[ωi1,ωi2,,ωiz]T为第i个隐层节点的输入权重；βi为第i个隐层节点的输出权重；bi为第i个隐层节点的偏置；oj为ELM网络模型的实际输出值。

(6)

上式可由矩阵表示为

Hβ=U

(7)

β=[β1,β2,…,βL]T，U=[u1,u2,…,uW]T

式中：H为ELM的隐层输出矩阵；β为输出权重矩阵；U为期望输出向量。

可采用最小二乘法求取最优权重向量β*使得实际输出与期望输出差值的平方和最小，其解为

β*=HΨU

(8)

式中：HΨ是矩阵H的Moore-Penrose广义逆。

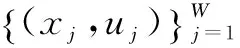
Ω=HHT，

Ωij=h(xi)·h(xj)=K(xi,xj),i,j=1,2,…,W

(9)

核矩阵Ω替代ELM中的随机矩阵HHT，利用核函数将z维输入样本映射到高维隐层特征空间。核函数K(xi,xj)是核矩阵Ω中第i行第j列的元素，包括RBF核函数、线性核函数和多项式核函数等，通常选择RBF核函数，其表达式为：

K(xi,xj)=exp(-γ(xi-xj)2),γ>0

(10)

式中：γ为核参数。

将参数I/C添加到HHT中的主对角线上，使其特征根不为零，并由此求权重向量β*为

β*=HT(I/C+HHT)-1U

(11)

式中：I为单位对角矩阵；C为惩罚系数，用于权衡结构风险和经验风险之间的比例。

可得KELM模型的实际输出为

(12)

式中：α=(I/C+HHT)-1U，为KELM网络的输出权值。

2　基于传递熵与KELM的风险传播路径分析方法

当过程出现异常工况产生扰动时，报警系统将通过声光形式的报警信号向操作者传递异常信息。报警通常由连续过程中存在的扰动引起。由于过程设备之间的关联性，扰动可能传播并影响大量过程变量，如果不能及时得到有效控制，可能导致风险的出现甚至灾难性的后果。因此，有必要分析过程变量间的关联关系，当报警发生时及时辨识并有效遏制风险传播途径。本文提出基于传递熵与KELM的炼油化工过程风险传播路径分析方法，如图2所示。针对某一工艺扰动分析风险传播过程，建立炼油化工过程风险传播推绎模型，提出一种风险传播搜索方法，预测风险传播路径，以便操作人员及时采取预防措施，保证炼油化工过程生产安全及产品质量。

2.1　炼油化工过程风险传播推绎模型

炼油化工过程工艺复杂，设备众多，同一过程设备及相邻设备间的监控变量往往具有关联性。采用传递熵分析方法可分析不同风险过程变量间的关联关系，推断他们固有的因果关系，从而建立炼油化工过程风险传播推绎模型，方法如下：

对于过程监控变量X和Y，变量Y到X的传递熵TY→X的计算公式如式(4)，Y到X的传递熵实质为Y的信息对于X不确定性大小的改变，即Y传递给X的信息量的大小。因此，传递熵可以作为衡量变量间因果性的指标。

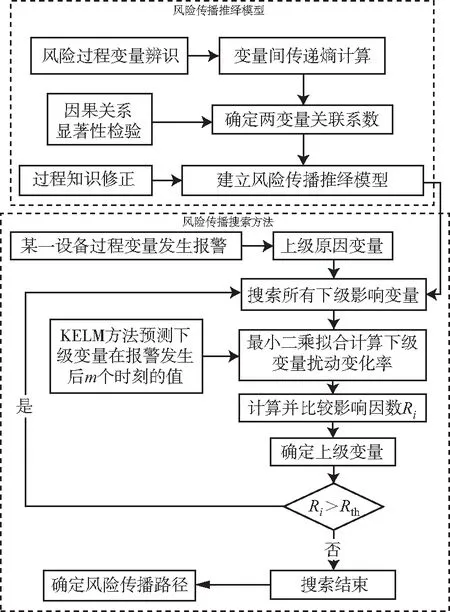
图2　基于传递熵与KELM的炼油化工过程风险传播路径分析方法流程Fig.2　Flowchart of the transfer entropy and KELM based risk propagation analysis method

同样，可求出变量X到Y的传递熵，2变量间的关联系数由式(13)确定：

(13)

如果ρX,Y=TY→X，表示2变量间传播方向为Y→X；如果ρX,Y=TX→Y，表示2变量间传播方向为X→Y；如果ρX,Y=0，表示2变量无因果关系。

因关联系数由统计方法计算得到，每两个时间序列可得到一确定值，但若TY→X与TX→Y的差值过小，考虑2变量间的因果性将没有意义。因此有必要设置合适的阈值对2变量间因果关系的显著性水平进行检验。本文采用如下的假设检验方法。

选取73个长度为200的随机生成序列，令tX→Y=TX→Y-TY→X，通过式(4)计算每两个序列间的tX→Y值，并求出所有|tX→Y|(tX→Y的绝对值)的均值μtX→Y和标准差σtX→Y，通过式(14)计算阈值[17]，判断2变量间因果关系的显著性。若关联系数没有通过显著性检验，表明2变量间不具备显著的因果性。

|tX→Y|-μtX→Y≥6σtX→Y

(14)

通过计算可得μtX→Y=0.053 5，σtX→Y=0.353。

对于N个风险过程变量X1，X2，…，XN，可通过计算传递熵确定其中每两变量的关联系数及传播方向，并据此建立风险传播推绎模型，如图3。模型由有向弧和代表风险过程变量的节点组成。对于任意2过程变量Xi和Xj，若tXi→Xj>0，有向弧由Xi指向Xj，即由上级原因变量指向下级影响变量；反之，则传播方向相反。

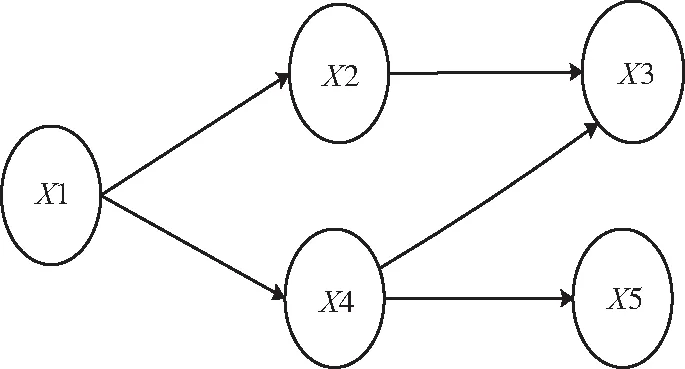
图3　风险传播推绎模型示意Fig. 3　Diagram of risk propagation reasoning model

最后结合过程知识检验传播路径的合理性，对模型进行适当修正。

2.2　风险传播搜索方法

过程变量发生报警通常由连续过程中存在的风险扰动引起。由于过程设备之间的关联性，扰动可能传播并影响大量过程变量，若不能及时得到有效控制，可能导致风险的出现甚至灾难性的后果。为此，提出一种风险传播搜索方法，以便当报警发生时及时辨识风险传播途径，提醒操作人员及时采取有效措施，避免异常风险的进一步发展。

风险传播搜索方法主要包括如下4个步骤：

步骤1：相同的报警可能产生不同的风险传播路径。为了准确辨识风险传播路径，当某一设备的过程变量Xj发生报警时，将其作为上级原因变量，根据2.1节所提方法建立的风险因素传播模型搜索与其直接相连的同设备及其相邻设备中所有下级影响变量节点，例如，图3中的X4报警，可搜索到其2个下级变量节点X3和X5。

步骤2：若变量Xj在tκ时刻发生扰动，对于Xj的各相关下级变量Xi(i=1，2，…，I;I为下级变量个数)，可通过式(15)计算变量Xi的扰动变化率，其值大小可近似反映各相关下级变量受上级变量扰动的影响大小。

扰动变化率(Disturbance Rate, DR)定义如下：

定义1：对于变量Xi，考虑以时刻tκ为中心，选择时间间隔为[tκ-m,tκ+m] (时间序列长度为2m+1)的变量Xi的时间序列进行最小二乘线性拟合如式(15)，所求斜率ai绝对值的大小作为变量Xi的扰动变化率。

其中，变量Xi在tκ+1至tκ+m时刻的值通过KELM方法预测得到，以变量Xi在tκ时刻前一段时间内(ts至tκ时刻)的历史数据构造KELM的训练样本，输入样本Xi*和输出样本U分别为

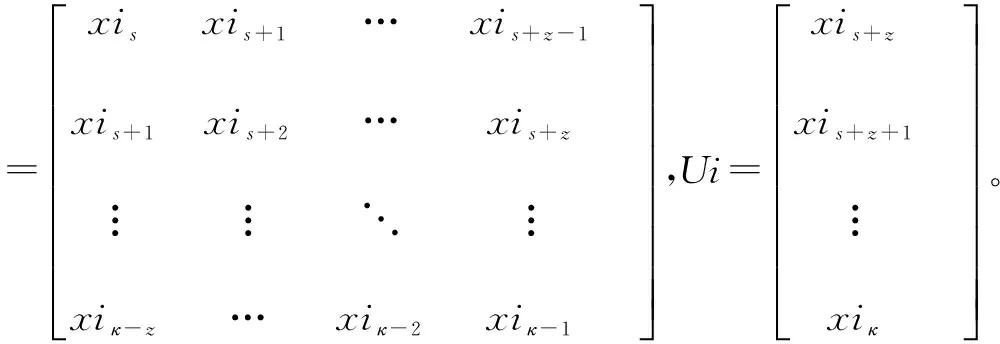
z为输入样本维数，样本个数为W=κ-z-s+1，xil(l=s,s+1,…,κ)为变量Xi在第tl时刻的值。

令xik=aitk+bi,其中，k=κ-m,…,κ,…,κ+m；tk=1,2，…,2m+1；i=1,2…,N；N为过程变量个数；xik为标准化后的变量Xi在第tk个时刻的变量值，最小二乘线性拟合公式如式(15)：

(15)

变量Xi的标准化公式如式(16)：

(16)

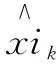
步骤3：通过式(13)计算两过程变量Xi和Xj间的关联系数，通过式(15)计算变量Xi的扰动变化率，基于所求关联系数和扰动变化率，根据式(17)计算上级变量Xj对各下级变量Xi的影响因数Ri，比较影响因数Ri的大小，将影响因数最大值对应的下级变量作为其下级影响变量。

下级变量的影响因数Ri越大，其受上级变量的影响越大，因此，通过Ri的大小可以比较上级变量对各相关下级变量产生扰动的影响大小，将Ri的最大值对应的下级变量作为其下级影响变量。若所求影响因数过小，说明该变量的时间序列数据趋于平稳，并受到上级变量影响，因此，根据专家经验及历史数据统计，如果Ri值小于阈值Rth(这里依据专家经验与历史统计，设为1.75)，将不考虑该下级变量。

(17)

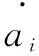
步骤4：重复步骤2和步骤3，依次确定可能受到风险影响的各设备过程变量并确定最可能的风险传播路径。

3　案例分析

催化裂化装置是炼油化工过程的关键装置。随着炼油厂生产规模的不断扩大，反应再生系统、分馏系统结焦、分馏塔冲塔、油浆泵故障等常导致催化裂化装置发生故障、非计划停机甚至灾害性事故。分馏单元是催化裂化生产装置的一部分，由反应器来的反应产物(油气)从底部进入分馏塔，油气经分馏后得到的富气、粗汽油、轻柴油、重柴油、回炼油及油浆。冲塔故障是分馏过程中经常发生的现象之一。当气液相负荷过大时，气体通过塔板的压降增大，会使降液管中液面高度增加，液相负荷增加时，出口堰上液面高度增加，当液体充满整个降液管时，上下塔板液体连成一片，分馏完全破坏，导致冲塔的发生。冲塔故障一旦发生，产品质量将受到严重影响。造成分馏塔冲塔的原因有很多，如塔盘掀翻或损坏、塔盘结盐、换热器故障、各种机泵故障等。为了保证产品质量，避免冲塔故障的发生，需分析冲塔风险，以下以某石化企业催化裂化分馏单元的冲塔风险过程为例，进行风险传播推绎分析。

3.1　冲塔过程风险传播推绎模型构建

就分馏塔冲塔风险而言，主要对分馏单元进行分析建模。催化裂化生产装置中的分馏单元主要包括分馏塔、分馏塔顶油气分离器、回炼油罐、原料油缓冲罐和轻柴油汽提塔。某石化企业催化裂化分馏单元的冲塔风险过程变量如表1所示。

表1　分馏单元冲塔风险过程变量

根据冲塔风险过程变量及某石化企业的历史数据(采样间隔为5 s，数据长度为1 000)，通过传递熵计算(见1.2节式(13))可得到分馏单元的冲塔风险过程变量间的关联系数，并依据式(14)判断2变量间因果关系的显著性；最后结合过程知识修正，建立冲塔过程风险传播推绎模型如图4。图4中各变量之间的关联系数如表2。

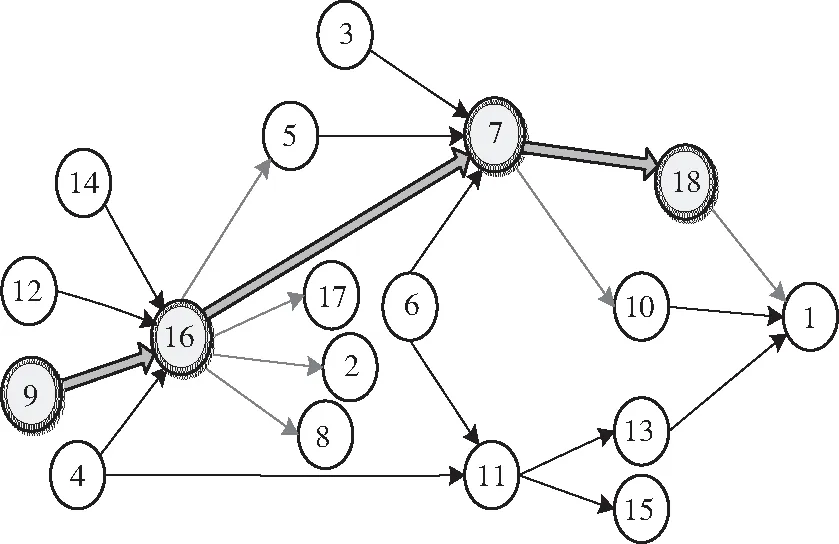
图4　冲塔过程风险传播推绎模型Fig.4　Risk propagation reasoning model in the flooding process

3.2　冲塔过程风险传播路径搜索分析

以一个发生在某石化公司的分馏塔冲塔事件为例，采用所提出的风险传播搜索方法进行分析。2016年8月23日，某石化公司催化裂化分馏塔发生冲塔，经现场人员调查分析，冲塔发生原因为一中回流泵故障，引起一中回流量过低发生低报警，使得分馏塔塔顶温度升高，重柴油侧线馏出口温度升高，分馏塔底液位过低，造成回炼油下返塔流量过低，操作人员发现回炼油下返塔流量过低后及时排查出了回流泵的故障原因，并采取措施使过程恢复到了正常运行状态。

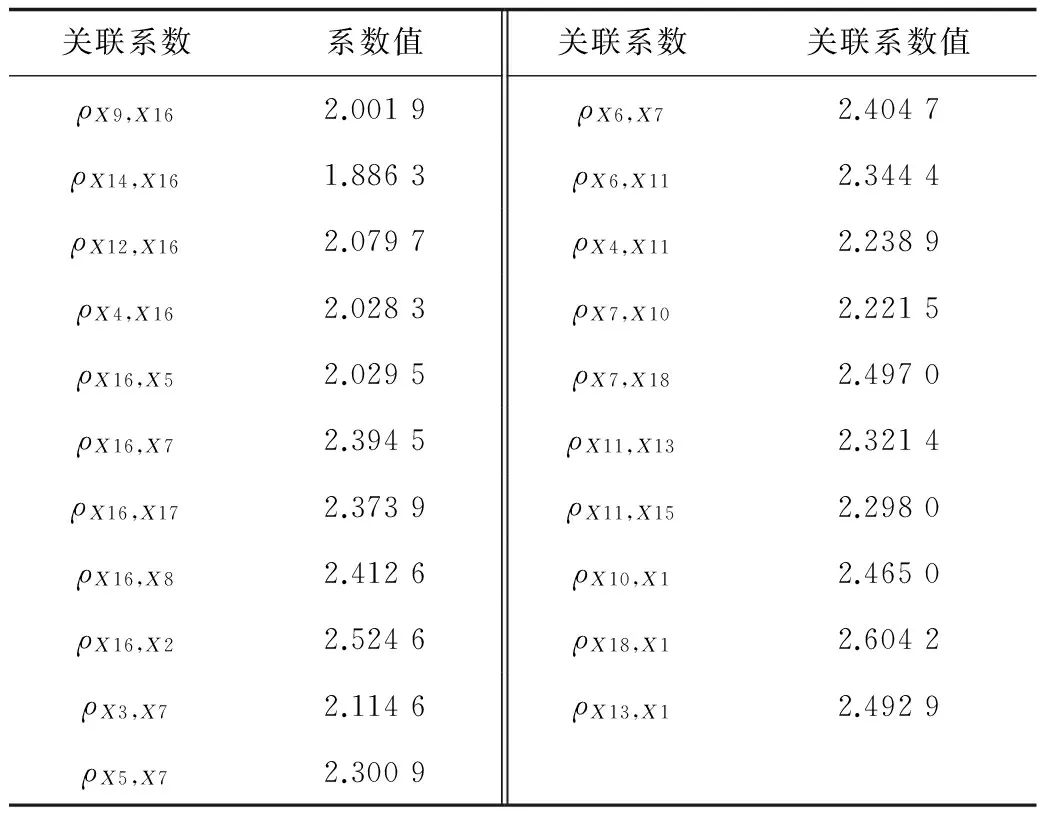
表2　各过程变量间关联系数

基于前文所建立的冲塔过程风险传播推绎模型，进行风险传播路径搜索分析，如图4所示：

步骤1：因一中回流量过低(节点9)发生报警，故将其作为上级变量，根据因果图搜索与其直接相连的下级变量分馏塔塔顶温度(节点16)。

步骤2：通过极限学习机预测方法预测节点9发生报警时刻后3分钟(共36个时刻)节点16的变量值，由式(15)可得其扰动变化率如表3所示，各变量时间序列的标准化后数据拟合曲线如图5，各变量单位见表1。

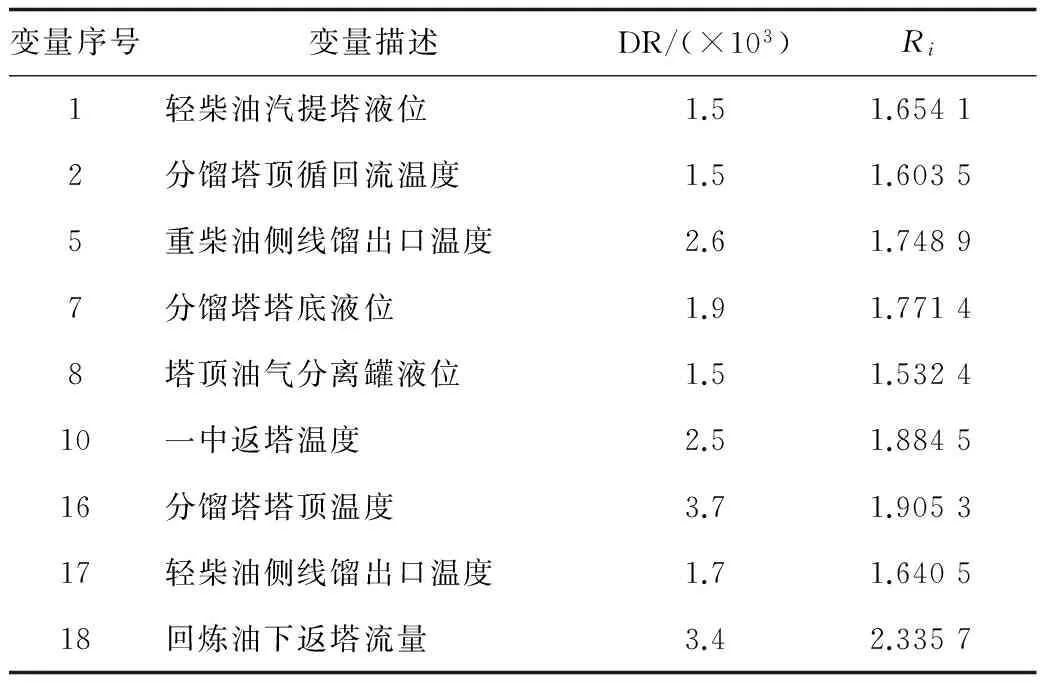
表3　各上级变量的扰动变化率及影响因数

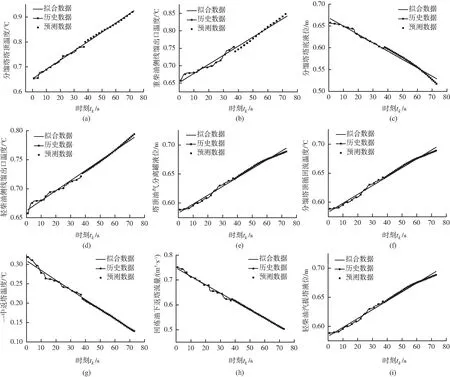
图5　各下级变量时间序列数据拟合曲线Fig. 5　Time sequence fitting curve of each subsequent variable

步骤3：根据式(17)计算节点16的影响因数如表3所示，因节点16的影响因数值Ri=1.905 3，大于阈值Rth(这里依据专家经验及历史统计设为1.75)，故将分馏塔塔顶温度(节点16)作为下级影响变量。

步骤4：继续搜索节点16的下级变量包括重柴油侧线馏出口温度(节点5)、分馏塔塔底液位(节点7)、轻柴油侧线馏出口温度(节点17)、塔顶油气分离罐液位(节点8)和分馏塔顶循回流温度(节点2)，通过极限学习机预测方法预测节点9发生报警时刻后3 min(共36个时刻)各节点的变量值，由式(15)及式(17)可得其扰动变化率及影响因数如表3所示，通过比较各相关下级变量的影响因数，其最大值为1.771 4，对应节点7，大于阈值Rth，因此将该最大值对应的下级变量分馏塔塔底液位(节点7)作为下级影响变量。继续搜索节点7的下级变量包括一中返塔温度(节点10)和回炼油下返塔流量(节点18)，由式(15)及式(17)可得其扰动变化率及影响因数如表3所示，通过比较各相关下级变量的影响因数，其最大值为2.335 7，对应节点18，大于阈值Rth，因此将该最大值对应的下级变量回炼油下返塔流量(节点18)作为下级影响变量。继续搜索节点18的下级变量轻柴油汽提塔液位(节点1)，由式(15)及式(17)可得其扰动变化率及影响因数如表3所示，因节点1的影响因数值Ri=1.654 1，小于阈值Rth，搜索结束。

3.3　结果分析

1)通过传递熵方法分析不同尺度下冲塔风险过程变量间的非线性关联关系及风险传播方向，采用所提风险传播搜索方法辨识出冲塔风险在整个分馏单元内的最可能传播路径为：一中回流量过低(节点9)→分馏塔塔顶温度(节点16)→分馏塔塔底液位(节点7)→回炼油下返塔流量(节点18)，该结论与前文所述的现场异常工况发生过程一致，从而验证了所提方法的有效性。

2)根据冲塔风险过程中2个上下级变量间的关联系数及下级变量的扰动变化率计算上级变量对下级变量的影响因数，影响因数的大小近似反映了上级变量对下级变量产生扰动的影响大小，有助于确定冲塔风险过程的传播路径，例如，节点7的下级变量包括一中返塔温度(节点10)和回炼油下返塔流量(节点18)，通过比较各相关下级变量的影响因数，其影响因数最大值对应的下级变量回炼油下返塔流量(节点18)即为节点7的下级影响变量。

3)采用所提方法对分馏塔冲塔过程风险传播路径进行分析，不仅考虑了存在冲塔风险设备分馏塔本身，还分析了分馏单元内与分馏塔存在关联的其他设备，避免遗漏某些可能受冲塔影响的风险过程变量，从而通过KELM预测风险传播路径，操作人员及时采取预防措施，合理规避风险。

4　结论

1)针对分馏塔冲塔风险过程，采用传递熵方法分析分析不同过程变量间的非线性关联关系及传播方向，建立了冲塔风险过程风险传播推绎模型，并基于KELM预测，提出一种风险传播搜索方法，可预测未来一段时间内风险的可能传播路径。

2)所提方法可辨识风险扰动传播给某些设备甚至整个生产单元带来的风险影响，有助于操作人员准确把握风险动态并及时采取合理措施抑制风险的进一步发展。

[1]DAHLSTRAND F. Consequence analysis theory for alarm analysis[J]. Knowledge-Based Systems, 2002, 15(1): 27-36.

[2]WAN Yiming, YANG Fan, LYU Ning, et al. Statistical root cause analysis of novel faults based on digraph models[J]. Chemical Engineering Research & Design, 2013, 91(1): 87-99.

[3]YANG Fan, SHAH S L, XIAO De-yun. Signed directed graph modeling of industrial processes and their validation by Data-Based methods[C]//2010 CONFERENCE ON CONTROL AND FAULT-TOLERANT SYSTEMS (SYSTOL'10)．Nice,France, 2010: 387-392.

[4]MAURYA M R, RENGASWAMY R, VENKATASUBRAMANIAN V. A systematic framework for the development and analysis of signed digraphs for chemical processes. 1. Algorithms and analysis[J]. Industrial & Engineering Chemistry Research, 2003, 42(20): 4789-4810.

[5]MAURYA M R, RENGASWAMY R, VENKATASUBRAMANIAN V. A systematic framework for the development and analysis of signed digraphs for chemical processes.2.Control loops and flowsheet analysis[J]. Industrial & Engineering Chemistry Research, 2003, 42(20): 4811-4827.

[6]HE Bo, CHEN Tao, YANG Xianhui. Root cause analysis in multivariate statistical process monitoring: Integrating reconstruction-based multivariate contribution analysis with fuzzy-signed directed graphs[J]. Computers & Chemical Engineering, 2014, 64: 167-177.

[7]MAURYA M R, RENGASWAMY R, VENKATASUBRAMANIAN V. A signed directed graph-based systematic framework for steady-state malfunction diagnosis inside control loops[J]. Chemical Engineering Science, 2006, 61(6): 1790-1810.

[8]CHANG C T, CHEN C Y. Fault diagnosis with automata generated languages[J]. Computers & Chemical Engineering, 2011, 35(2): 329-341.

[9]BAUER M, THORNHILL N F. A practical method for identifying the propagation path of plant-wide disturbances[J]. Journal of Process Control, 2008, 18(7): 707-719.

[10]HAN Liu, GAO Huihui, XU Yuan, et al. Combining FAP, MAP and correlation analysis for multivariate alarm thresholds optimization in industrial process[J]. Journal of Loss Prevention in the Process Industries, 2016, 40: 471-478.

[11]GAO Huihui, XU Yuan, GU Xiangbai, et al. Systematic rationalization approach for multivariate correlated alarms based on interpretive structural modeling and Likert scale[J]. Chinese Journal of Chemical Engineering, 2015, 23(12): 1987-1996.

[12]ABELE L, ANIC M, GUTMANN T, et al. Combining Knowledge Mo￣deling and Machine Learning for Alarm Root Cause Analysis[J]. IFAC Proceedings Volumes, 2013, 46(9):1843-1848.

[13]GAO J, TULSYAN A, YANG F, et al. A transfer entropy method to quantify causality in stochastic nonlinear systems[J]. IFAC-PapersOnLine, 2016, 49(7): 454-459.

[14]ZHAO Xiaojun, SHANG Pengjian, LIN Aijing. Transfer mutual information: A new method for measuring information transfer to the interactions of time series[J]. Physica a: Statistical Mechanics and Its Applications, 2017, 467: 517-526.

[15]SCHREIBER T. Measuring information transfer[J]. Physical Review Letters, 2000, 85(2): 461-464.

[16]HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489-501.

[17] HAJIHOSSEINI P, SALAHSHOOR K, MOSHIRI B. Process fault isolation based on transfer entropy algorithm[J]. ISA Transactions, 2014, 53(2): 230-240.