非饱和岩土材料的固流转化数值模拟

吕　谦，李兆华

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.深部岩土力学与地下工程国家重点实验室，北京 100083)

0　引　言

一般来说，非饱和岩土材料表现出固态的弹塑性力学特性，可以由各种现有的弹塑性本构模型来描述[1]。然而，在破坏发生后，随着动能的突增，一些近饱和的松散岩土体也往往会表现出类似流体的力学特征。从微观角度讲，滑坡的发生过程可以解释为岩土颗粒系统由“强接触”向“弱接触”转变的过程，即抗剪强度突降而剪切应变快速发展。为了实现滑坡从启动、扩展到停滞全过程的模拟，许多学者针对非饱和岩土材料建立了一个考虑水力耦合作用的黏弹塑性固流转化模型[2-3]。该模型既可以描述非饱和岩土介质在破坏前的固体弹塑性力学特性，也可以描述破坏后的流体黏性力学特性，介于两种状态之间，引入了一个破坏准则作为该模型固流转化的判别准则。该固流转化统一模型详细情况可参见文献[3]。

现有的数值方法无法在同一个框架下准确地处理固流两个问题，于是一些学者将滑坡现象分成两个不同的阶段来进行研究[4]。处理此类问题要求数值方法能够准确计算各种力学行为，尤其是滑动过程中的大变形问题。为满足上述要求，多种颗粒点法应运而生。物质点有限元法(PFEM)[5]是一种使用mesh-less有限元插值函数的方法。

此外，物质点法(MPM)吸取了拉格朗日方法和欧拉方法的长处，计算域被离散为一系列可自由移动的物质点，牛顿第二定律作为控制方程并用以计算固定网格上的速度场。这种方法较频繁地应用在滑坡模拟中[6]，但存在缺点。

确定了宏观本构模型后，只要流动过程中没有明显的不连续现象，基于连续介质力学的数值方法仍是有效的。本文选择拉格朗日积分点有限元法(FEMLIP)对非饱和岩土介质的固流转化现象进行研究，该方法由质点网格法发展而来[7]，吸取拉格朗日和欧拉方法两者的优势，既可以计算存储弹塑性变量的问题又可以处理大变形问题[8-9]。

1　考虑水力耦合的非饱和岩土材料固流转化统一模型

对于降雨诱发的滑坡，细粒土在破坏前表现出固体力学特性，而破坏后往往表现为流体的黏性流动。由李兆华等[3]提出的固流转化统一模型可用于这一类型的模拟。如图1所示，这个三维模型可由一维的形式表现出来。图1中“d2W”指二阶功[9]。

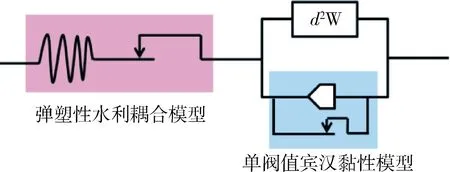
图1　非饱和岩土材料固流转化三维模型的一维形式

如图1所示，饱和或非饱和多孔介质使用弹塑性模型来描述，水力耦合计算通过引入有效应力和水分特征曲线来实现。需要指出的是，该模型使用二阶功作为破坏准则，可以描述分岔破坏理论中的扩散破坏、应变集中破坏和塑形极限破坏。

1.1　考虑水力耦合的弹塑性模型

1.1.1毕肖普有效应力

对于非饱和多孔介质，关于应力变量选取的问题在国际范围内一直没有定论。本文采用的固流统一模型使用毕肖普有效应力来描述非饱和多孔介质，见式(1)。

σ′=σ-uam+χ(ua-uw)m

(1)

式中：σ′、σ、ua和uw分别为有效应力矢量、总应力矢量、孔隙气压力和孔隙水压力；χ为毕肖普参数，这里mT是一个标量。mT=(1,1,1,0,0,0)，s=ua-uw是基质吸力。毕肖普参数通常表达为χ=Sr，Sr是饱和度，但该表达式所反应的是一个理想介质,而不是实际的多孔介质。根据Alonso等的提议[10]，χ可以由aχ和nχ两个参数确定，通过适当地定义这两个参数可以描述非饱和土浸润过程中的塑形破坏现象。

新的毕肖普参数χ的公式，见式(2)。

(2)

式中：s为基质吸力;Patm为大气压力。通过适当定义aχ和nχ,毕肖普参数χ可以描述非饱和土的很多特性。

1.1.2PLASOL弹塑性模型

这里使用弹塑性模型PLASOL来模拟非饱和岩土材料破坏前的力学行为。该模型采用Van Eekelen准则作为屈服面及塑性极限破坏准则，VE屈服面接近于摩尔库伦屈服面。该屈服面公式，见式(3)。

(3)

m=a(1+bsin(3β))n

(4)

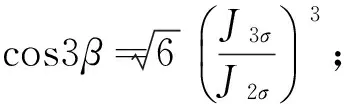
(5)

式中：参数n用来控制屈服面形状，根据Van Eekelen的建议将其默认为-0.299;参数rc和re分别为三轴压缩和拉伸试验简化半径，计算公式见式(6)。

(6)

式中φe为三轴拉伸路径下的修正内摩擦角。

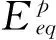
区别于屈服面的不相关联塑性流动法则计算见式(8)。

(8)

式中：m′与屈服面公式中的m形式相同;φc和φe由压缩、拉伸路径下的剪胀角ψc和ψe替代。

1.1.3水分特征曲线

水分特征曲线(WRC)反应了非饱和岩土介质中基质吸力和饱和度或含水量之间的水力关系。

如图2所示，一个完整的水分特征曲线通常包括边界干燥曲线、边界浸润曲线和扫描曲线。这里我们使用修正VanGenuchten-Mualem模型，该模型考虑了回滞效应及孔隙率对饱和度的影响，其边界曲线公式见(9)。

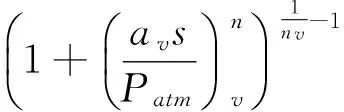
(9)

式中：下标v为浸润过程;d为干燥过程;Srres,Srsat和Srv分别为残余饱和度、饱和状态下的饱和度及当前饱和度;av和nv为两个参数，av定义如(10)所示;saev与n相关，定义如式(11)所示。

(11)

式中：saev0为参考孔隙率n0对应的空气进入量值;λ为一个物理参数。如此，建立了一个基质吸力及孔隙率相关的水力模型。

图2　非饱和岩土介质水分特征曲线图

1.2　固流转化准则

根据分岔破坏理论，岩土材料的塑性流动具有明显不相关联性。根据分岔破坏的定义，极小的扰动荷载可能导致突然或不连续的反应。这里我们选用该准则作为岩土材料的破坏准则和固流转化准则，其公式见式(12)。

(12)

式中σ′和ε分别为有效应力张量和应变张量。

二阶功由有效应力增量计算得来，以便分析土骨架的失稳问题。如果对于所有加载方向，当d2w>0,则材料处于稳定状态。否则在二阶功小于等于零的加载方向上可能发生应变集中破坏或扩散破坏。式(12)所表述的局部二阶功在各积分点上计算,并用以判断材料的局部破坏情况，为了分析边值问题，按式(13)计算整体二阶功。

(13)

式中：ωi为积分点i的数值权重;Ji为雅可比矩阵行列式。式(13)求出的整体二阶功,通常被用来判断岩土体的整体破坏情况。

1.3　宾汉黏性模型

岩土材料在破坏后可以由单一阀值sy的宾汉黏性模型来描述。根据Duvaut和Lions及Balmforth和Craster的公式,三维简化宾汉黏性模型表达，见式(14)。

如果

(14)

否则

如图3所示，宾汉应力阀值通常小于Van Eekelen弹性极限，而二阶功在弹性极限范围内总是正值，故一般情况下二阶功可认为是岩土材料固流转化的准则。

2　基于拉格朗日积分点有限元的水力耦合方法

本研究使用拉格朗日积分点(FEMLIP)有限元法进行数值分析。如图4(a)、图4(b)所示，计算域通过欧拉网格进行离散化，而岩土材料采用拉格朗日物质点进行空间离散化。各个计算步结束时，物质点根据插值所得的速度场更新位置以体现材料的变形，而网格本身不会发生变形，如图4(d)所示。这样可以处理大变形问题而避免网格畸变现象。

图3　主应力空间下的固流统一模型

图4　FEMLIP方法计算过程

2.1　控制方程

非饱和岩土材料是一种可压缩的三相介质，即由岩土框架、水和空气组成的固相、液相和气相三相介质。简化后的控制方程由平衡方程和液相连续方程组成，平衡方程的表示形式见式(15)。液相连续方程由水的质量守恒方程和广义达西定律组成，见式(16)。

(16)

式中：S和V分别为面力f作用的边界和单元体积;σ为柯西总应力张量；b为重力引起的体应力矢量；g为重力加速度；ρw为水密度；bw为孔隙水的体力矢量；uw为孔隙水压力；k为非饱和岩土体的渗透率矩阵。

2.2　增量本构关系

(17)

(18)

应当注意，为了简化起见，假设当Δt足够小时,χ是恒定的。含水量表示为θ=n·Sr，用修正Van Genuchten-Mualem模型建立含水量-基质吸力关系，见式(19)。

(19)

组合式(19)和式(20)，矩阵关系如式(20)所示。

(20)

(21)

2.3　FEMLIP模型公式

利用线性和常量函数N和Nw分别插值速度和水压力场，基于控制方程和式(20)，离散有限元方程见式(22)。

(22)

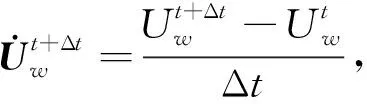
(23)

3　FEMLIP模拟和分析

本文给出了一个重力状态下初始稳定的非饱和土柱的数值分析。该土柱面积为6 m×6 m，初始基质吸力为500 kPa,且均匀分布。土体用一系列物质点离散化。所有边界均可自由滑动，土体顶部表面的降雨(持续79 h)以1.8 mm/h(5×10-7m/s)的恒定入渗水力边界条件模拟。

系数为简化起见，在FEMLIP模型中，边坡的渗透系数假定为各向同性，非饱和土的渗透率k由k=kr·ks确定，ks为饱和土的渗透系数，kr为相对水力传导系数。在本文中，使用Van Genuchten提出的公式确定kr。

3.1　吸力和渗透性的建模与分析

表1和表2为模拟所需要的参数，在表2中，ks为饱和土的初始渗透系数。使用式(22)控制非饱和土的渗透系数。水力梯度和非饱和土的渗透系数使得水从介质的顶部向底部渗透。选择边坡表面(A)、中部(B)和底部(C)三个位置来观察渗透效果，如图5(a)、图5(b)所示。需要指出，这次分析暂不考虑固流转化。

表1　弹塑性参数

表2　液压和水力耦合参数

图5　不同水压边界条件下的非饱和土柱

图6给出了点A、点B、点C在两种不同初始渗透系数ks=1×10-3m/s和ks=1×10-4m/s基质吸力变化情况。因为雨水需要较长时间才能渗透至比较深的地下，所以表面的基质吸力比底部小。土体表面的基质吸力变化量取决于水量，然而，根据达西定律， 渗透地面的水量部分受非饱和土壤渗透率的控制。图7为非饱和渗透系数相对于时间的变化。对于较高的饱和渗透系数ks=1×10-3m/s，使用式(22)确定初始非饱和渗透率为5×10-7m/s，近似等于入渗水量。这表明水可以完全渗透进土体。而对于较低饱和渗透系数ks=1×10-4m/s，所计算的非饱和渗透率约等于6×10-8m/s，明显小于水量。因此，在这种情况下，只有部分水渗入土体。

3.2　固流转化的模拟和分析

如果固流转化产生，且达到破坏时土柱由弹塑性固体形态转为黏性流体形态。图5(b)所示在长为5 m的E-F边界，以入渗速度为10-6m/s(3.6 mm/h)下模拟固流发生的过程。最初和最终的有效黏聚力c′0为0 kPa、10 kPa、25 kPa和c′f为0 kPa、25 kPa、45k Pa。表3和表4列出了用于模拟的附加参数。

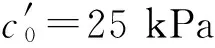
图6　在饱和渗透系数1×10-3 m/s和1×10-4 m/s下 点A、点B、点C的基质吸力变化曲线

图7　在饱和渗透系数1×10-3 m/s和1×10-4 m/s下 点A、点B、点C的非饱和渗透系数曲线

表3　弹塑性参数

土体参数Eνφe0=φc0φef=φcfψe=ψcBpBcρηsy值50.351525100.010.02110015012

表4　水力耦合参数

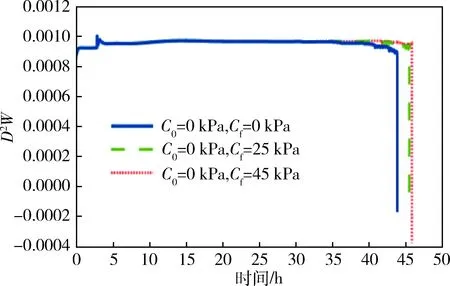
图8　有效凝聚力对破坏的影响

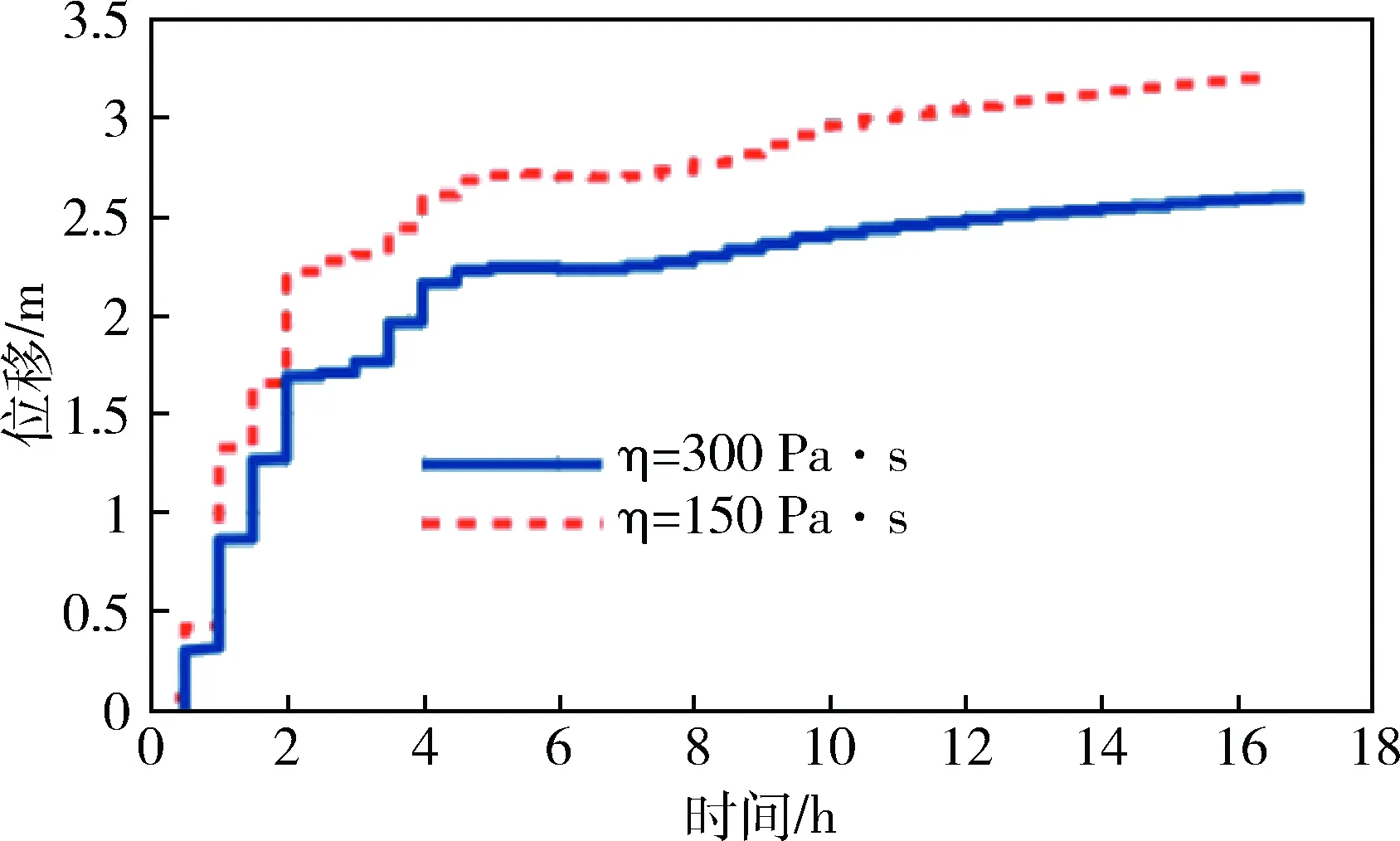
图9　黏度系数对水平位移的影响

图10　(a)～(d)破坏前阶段基质吸力云图及(e)～(f)破坏后阶段土体流动形态

4　结　论

本研究将非饱和岩土材料固流转化模型应用到拉格朗日积分点有限元中，并提出一个新的可用于模拟高速滑坡或泥石流的FEMLIP模型。

为了验证该FEMLIP模型，首先对一个具有均匀分布初始基质吸力的非饱和土柱进行模拟，分析了不同渗透系数对基质吸力变化的影响。之后对水力边界条件下土体固流转化现象进行模拟，并分析了黏聚力和黏度系数对固流转化和流动速度的影响。基于研究结果， FEMLIP模型在描述非饱和土

体的固体和流体状态行为方面是有效的。

[1]杨光华,姚捷,温勇.考虑拟弹性塑性变形的土体弹塑性本构模型[J].岩土工程学报,2013(8):1496-1503.

[2]熊威,甘忠,许旭东,等.基于粘弹塑性模型的时效成形仿真[J].塑性工程学报,2012(2):33-37.

[3]LI Z H,DUFOUR F,DARVE F.Hydro-elasto-plastic modeling with a solid/fluid transition[J].Computers and Geotechnics,2016,75:69-79.

[4]ALONSO E E,GENS A,DELAHYTE C.Influence of rainfall on the deformation and stability of a slope in over consolidated clays:a case study[J].Hydrogeology Journal,2003,11:174-192.

[5]ZHANG X,KRAB benhoft K,SHENG D,et al.Numerical simulation of a flow-like land slide using the particle finiteelement method[J].Computational Mechanics,2015,55(1):167-177.

[6]ABE K,SOGA K,BANDARA S.Material point method for coupled hydromechanical problems[J].Journal of Geotechnical and Geoenvironmental Engineering,2014,140(3)：1-15.

[7]MORESI L,DUFOUR F,MUHLHAUS H B.Mantle convection modeling with viscoelastic/brittle lithosphere:numerical methodology and platetectonic modeling[J].Pureand Applied Geophysics,2002,159(10):2335-2356.

[8]HARLOW F H.The particle-in-cell computing method for fluid dynamics[J].Computer Methods in Physics,1964,3:319-343.

[9]PRIME N,DUFOUR F,DARAVE F.Unified model for gromateria solid/fluid states and the transition in between[J].Journal of Engineering Mechanics,2014，140(6):682-694.

[10]ALONSO E E,PEREIRA J M,VAUNAT J,et al.Amicrostructurally based effective stress for unsaturated soils[J].Géotechnique,2010,60(12):913-925.

更正说明

我刊2016年第25卷第11期(总第231期)《俄罗斯大陆架地质调查及矿产资源开发利用现状》，作者：王淑玲，王铭晗，邵明娟，吴西顺，张炜，贾凌霄；工作单位：中国地质图书馆·中国地质调查局地学文献中心；页码：28～34，82。该文由中国地质调查项目“地学情报综合研究与产品研发”资助(编号：121201015000150002)。

特此说明。

中国矿业杂志社编辑部