基于博弈论和D-S证据理论的城市防洪标准方案决策优选方法

2018-04-13胡向阳李文俊

中国农村水利水电 2018年3期

邹　强，胡向阳，李文俊

(长江勘测规划设计研究有限责任公司水利规划研究院，武汉 430010)

0　引　言

城市防洪是大多数城市防御自然灾害面临的首要问题，在海绵城市建设背景下，全国城市防洪安全问题受到密切关注，城市防洪标准确立及防洪工程体系构筑的重要性日益凸显。城市防洪标准为系统运用工程措施和非工程措施后防御大洪水的能力，通常表达为所能防御的洪水频率或其重现期[1]。而城市防洪标准方案决策优选是城市防洪规划的首要问题，也是城市洪灾风险管理的重要环节，其实质是遵循政治、社会、经济和环境效益综合最优原则来构建综合评价指标体系，从有限的城市防洪方案标准集中选出相对最优方案[2,3]。该复杂决策过程呈现多目标、多阶段、多层次特征，且指标体系存在模糊、随机、未确知等不确定性，其关键在于指标权重的综合确定和不确定性的有效处理[4-6]。

针对综合权重的确定，常规计算手段是首先分别获得反映决策者意念的主观权重和反映数据分布规律的客观权重，然后依据加法法则、乘法法则等处理基本主客观权重，以获得综合权重[1,6]。但随着研究的深入以及各种权重计算方法的提出，比如层次分析法[1]、二元分析法[3]及其改进等主观权重计算方法，以及投影寻踪[4]、熵值法[6]及其改进等客观权重计算方法，不同权重赋值途径各异，有必要针对不同方法的权重结果开展有效地博弈集结，来综合利用各方面的指标权重信息[7]。而博弈论正好能较好地解决该问题，通过极小化综合权重与各种基本权重之间的偏差，获得较为一致的最满意权重或综合权重[7,8]。另一方面，城市防洪标准方案决策优选方法较多，如模糊综合评价模型[2,3]、投影寻踪模型[4]、最大熵评价模型[5]、熵权与改进理想解法耦合模型[6]等，各种方法都有各自的优点和不足。比如投影寻踪模型中窗宽选取有进一步优化的空间；模糊综合评价模型中隶属度函数的选取具有人为主观性；相关方法与智能优化算法结合时，不易编程实现；且上述方法都存在一定程度的不确定性，如何克服人为主观的干扰、降低评估结果的不确定性亟待研究。而D-S证据理论可通过数据融合来充分利用各种信息，减少评价过程中的不确定性[9]，已成功应用到投资决策[10]、安全评估[11,12]和水库调度评价[13]等决策问题。

为此，本文尝试将博弈论和D-S证据理论应用到城市防洪标准方案优选中，来有效处理复杂决策过程中存在的权重计算、不确定性处理等难点，以提高评价信息的利用率和降低评价的不确定性，最终实现方案优劣排序。实例研究验证了提出方法的适用性和有效性，提高了城市防洪标准方案决策优选的合理性和科学性，具有良好的理论意义和应用价值。

1　基于博弈论的综合权重确定

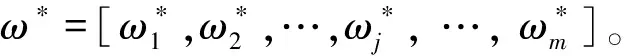
首先，分别采用主观、客观共K种不同方法计算权重，得到m个评价指标的权重向量：

ωk=[ωk1,ωk2,…,ωkj,…,ωkm]

(1)

k=1,2,…,K,j=1,2,…,m

这样可构造K种评价方法的权重矢量场{ω1,ω2,…,ωk}。现通过权重矢量场的任意线性组合系数α*=[α1,α2,…,αK]来获得ω*，以有机集化、融合各种方法的权重信息：

(2)

然后，依据博弈论，在各种指标权重之间寻找协调、均衡、妥协，可使ω*与各种ωk之间的各自偏差达到最小。也就是说，必存在一个最满意的线性组合，使得ω*与ωk(k=1,2,…,K)的离差最小，便可导出以下多目标博弈集合模型：

(3)

根据矩阵的微分性质，得到上述模型的最优化一阶导数条件：

(4)

其次，为方便分析，式(4)对应的矩阵形式表达为：

(5)

求解式(5)，可得线性组合系数α*=[α1,α2,…,αK]。通常情况下α*均是正值；但若为负值，则将其取绝对值转换为正值，并对作如式(6)的规格化处理[7]：

(6)

最终综合权重计算公式如下：

(7)

2　D-S证据理论

2.1　D-S证据理论基本定义

D-S证据理论(Dempster-Shafer Evidence Theory)是一种不确定性处理方法，率先于20世纪60年代由Dempster提出，后来由其学生Shafer系统地补充和完善[9]。D-S证据理论的核心内容是可有效表征不确定事件的不确定性度量，并通过不确定性的推理和融合以达到降低不确定性、提高决策精度的目的[10-13]。以下给出D-S证据理论的相关概念[10]：

(1)定义1(识别框架)。Θ为一识别框架，是关于命题的所有相互独立的一个有限集合或可能答案，并且假设所有可能的答案中有且只有一个是正确的。

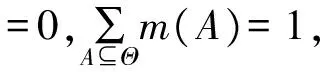
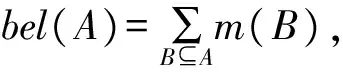
(4)定义4(证据合成法则)。对于∀A⊆Θ，证据m1,m2,…,mn为Θ下的Mass函数，则对于两个及多个Mass函数合成法则为：

(m1⊕m2⊕…⊕mn)(A)=

(8)

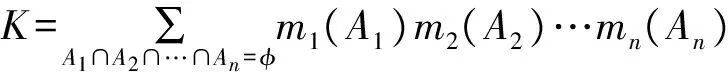
2.2　Mass函数的确定

Mass函数是D-S证据理论的运算基础，本文结合灰色关联法来计算Mass函数[11,13]。设城市防洪标准方案集共n个，记为X={A1,…,Ai,…,An}；各方案均有m个评价指标，记为I={I1,…,Ij,…,Im}；第i个方案的j指标的特征值为xij，则评价决策矩阵记为X={xij}n×m。由于各评价指标量纲各异，需对原始特征值xij进行规范化处理。若为效益型指标，采取式(9)；若为成本型指标，采取式(10)：

(9)

(10)

式中：yij为xij的规范化值，有0≤yij≤1，得到无量纲决策矩阵Y=(yij)n×m。在此基础上，将博弈论确定的综合权重ω*代入到Y，得到加权决策矩阵U=(uij)n×m：

(11)

以正理想方案A+和负理想方案A-作为灰色关联分析的参考数列：

(12)

可见，正理想方案是指标均为最大值时的方案；负理想方案是指标均为最小值时的方案。进一步，根据灰色关联分析，以正、负理想方案作为参考数列，将方案Ai作为被比较数列，构建Ai与A+和A-关于指标Ij的关联系数分别为：

(13)

(14)

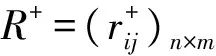
在正、负灰色关联系数矩阵的基础上，由式(16)得到综合灰色关联系数R=(rij)n×m为[11]：

(15)

指标j下的q阶不确定度计算公式为：

(16)

式中，一般取q=2，rij为综合灰色关联系数。则各指标下不同方案的Mass函数为：

mj(i)=[1-DOI(Ij)]×uij

(17)

(18)

2.3　Mass函数的调整

确定Mass函数后，将依据证据合成法则式(8)进行融合推理。但由于证据集中各指标的权重各异，需理清关键指标和非关键指标的区别，而不能在证据合成时均等对待，即强化关键指标的作用，对证据引入可信度系数处理，来表征各项证据的可信程度，则修正调整的Mass函数为[12]：

(19)

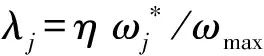
(20)

最终应用证据合成法则对M进行融合，并依据信度函数对方案排序优选[10-13]。

3　基于博弈论和D-S证据理论的方案决策优选方法

结合博弈论确定综合权重、D-S证据理论中Mass函数确定和融合的详细过程，以下是基于博弈论和D-S证据理论的城市防洪标准方案决策优选的详细步骤：

(1)依据城市防洪标准方案，确定评价决策矩阵X=(xij)n×m，并由式(9)或(10)对指标进行规范化处理，形成无量纲决策矩阵Y=(yij)n×m。

(2)由不同方法得到评价指标的主观、客观两类权重，依据博弈论，由式(1)～(7)得到评价指标的综合权重ω*。

(3)由式(11)得到加权决策矩阵U=(uij)n×m，并由式(12)得到正、负理想方案A+和A-。

(4)由式(13)和(14)得到正、负灰色关联系数矩阵R+和R-，并由(15)得到综合灰色关联系数矩阵R，进而由(16)得到指标j下的不确定度DOI(Ij)。

(6)运用证据合成法则(8)，对所有Mass函数组成的矩阵M进行融合。

(7)依据融合后置信函数值对城市防洪标准方案集进行优劣排序。

4　实例研究

4.1　评价指标

为验证提出方法的可行性和有效性，以中国南方某重点城市的防洪标准方案决策优选问题开展研究。该城市非农业人口共368万人，在1915年曾发生过800年一遇的特大洪水，造成了非常严重的洪灾损失。综合考虑政治、社会、经济和生态环境效益等多方面因素，建立了该城市200、300、500和800年一遇的防洪标准方案集，其评价指标体系及其规范化特征值详见表1[4-6]。现给出基于博弈论和D-S证据理论的城市防洪标准方案决策过程。

4.2　计算分析

(1) 由表1，该城市防洪标准方案集包括4个方案，12个评价指标，即n=4，m=12，形成无量纲决策矩阵Y=(yij)4×12。

(2) 通过广泛查阅该实例研究的研究文献并归纳汇总，获取了层次分析法(AHP)[4,5]、二元对比法[5,6]、基于加速遗传算法的改进层次分析法(AGA-AHP)[1,4,5]、基于加速遗传算法的投影寻踪模型(AGA-PP)[1,4]、熵权法[6]共5种不同方法的权重，详见表2。

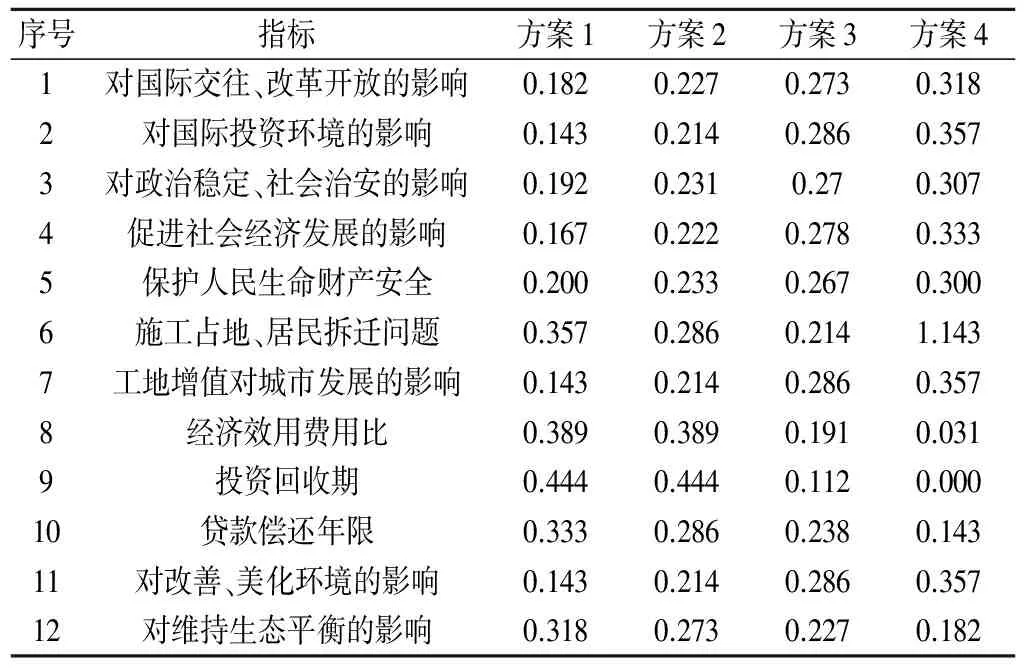
表1　城市防洪标准方案集及其规范化评价指标一览表Tab.1 Urban flood control standard schemes and their standardized evaluation indexes

表2　不同方法的评价指标权重Tab.2 Weights of the evaluation indexes by different methods

由表2可知，既有AHP、二元对比法和AGA-AHP这3个主观赋权方法，又有AGA-PP、赋权法这2个客观赋权方法。显然，指标权重直接影响决策优选结果，如果只是采用上述一种方法而忽视了其他评价方法的计算权重，评价结果有失全面性和科学性，尚需开展以上多种权重结果的有效融合，为此，本次采用博弈论来确定综合指标权重，以有机结合和全面利用各种权重信息。

由式(5)和(6)得到线性组合系数：

α*=[α1,α2,…,α5]=

[0.140 7, 0.324 9, 0.277 1, 0.115 0, 0.142 3]

可通过α*线性组合赋权方式(7)，最终的综合权重为：

ω*=[0.103, 0.093, 0.111, 0.114, 0.150, 0.059,

0.071,0.068,0.062,0.062,0.058,0.047]

(3) 由式(11)～(12)确定正、负理想方案A+和A-：

(4) 由式(13)～(16)得到各指标的不确定度：

DOI(I1)=0.133,DOI(I2)=0.139,DOI(I3)=0.132,

DOI(I4)=0.138,DOI(I5)=0.134,DOI(I6)=0.221,

DOI(I7)=0.135,DOI(I8)=0.133,DOI(I9)=0.145,

DOI(I10)=0.126,DOI(I11)=0.132,DOI(I12=0.127)

(5) 由式(17)～(20)，形成方案集决策优选的Mass函数矩阵M：

其中，整体不确定度的Mass函数为：

(6) 令识别框架Θ={A1,A2,A3,A4}，并取2Θ={{A1},{A2},{A3},{A4},{A1,A2,A3,A4}}，依据式(8)的证据合成法则，得到合成后Θ内各子集的信度函数分别为：

bel(A1)=(m1⊕m2⊕…⊕m12)(A1)=0.161 4

bel(A2)=(m1⊕m2⊕…⊕m12)(A2)=0.215 9

bel(A3)=(m1⊕m2⊕…⊕m12)(A3)=0.220 4

bel(A4)=(m1⊕m2⊕…⊕m12)(A4)=0.383 6

bel(A1,A2,A3,A4)=

(m1⊕m2⊕…⊕m12)(A1,A2,A3,A4)=0.018 7

根据信度函数最大化原则，对4个城市防洪标准方案A1,A2,A3,A4，其决策优选排序结果为A4>A3>A2>A1。这与模糊综合评价模型[2,3]、投影寻踪模型[4]、最大熵评价模型[5]、熵权与改进理想解法耦合模型[6]等方法的排序结果是完全一致的，均认为方案4为最佳方案，即该城市防洪标准应确定为800年一遇。

进一步，分析比较可知，在信息融合过程中，整体不确定性的信度值由最初的平均值54.77%降低到1.87%，表明通过D-S证据理论处理方案集决策优选问题时，可显著降低信息的不确定性，提高科学决策水平，具有很好的可行性和有效性。

5　结　论

本文提出了一种基于博弈论和D-S证据理论的城市防洪标准方案决策优选方法，具有两方面优势：①兼顾主、客观两类权重的优点，引入博弈论将多种主客观权重结果进行均衡融合，使得评价指标的综合权重更具科学性和全面性；②将D-S证据理论应用于决策优选过程中，通过不确定信息的精确描述和推理合成，来显著降低信息的不确定性和提高决策的科学合理性，并依据可信度函数来实现决策排序。实例研究验证了该方法的可行性和有效性，为城市防洪标准方案决策提供了一种科学合理而又行之有效的工具。

当然，建立具有普适性且能全面贯彻海绵城市建设要求的城市防洪标准综合评价指标体系，一直是学术界和工程界的难点问题，将在下一步重点研究；随着D-S证据理论研究的不断深入，应针对证据高冲突下证据合成法则有效改进开展具体研究，以进一步提高对不确定性的诊断能力。

□

参考文献：

[1]金菊良, 吴永林, 汪明武.城市防洪标准方案优选的组合权重方法[J].四川大学学报(工程科学版), 2004,36(4):1-5.

[2]殷峻暹, 陈守煜, 梁国华.应用模糊决策分析理论确定城市防洪标准研究[J].水电能源科学, 2001,19(3):52-54.

[3]周振民, 韩冬梅.模糊优选理论在城市防洪标准选择中的应用[J].人民长江, 2008,39(24):20-22.

[4]吴成国, 金菊良, 魏一鸣, 等.城市防洪标准方案优选的最大信息熵原理与投影寻踪耦合模型[J].中国管理科学, 2008,16(S1):1-4.

[5]范秋映, 金菊良, 周玉良,等.基于最大熵原理的城市防洪标准方案优选智能评价模型[J].安全与环境学报, 2009,9(2):154-157.

[6]唐言明, 卜松, 董洪茂, 等.城市防洪标准方案优选的熵权与改进理想点法耦合模型[J].人民珠江, 2016,37(7):49-52.

[7]苏观南, 付修庆, 刘天祥.改进的博弈论综合权重在大坝安全综合评价中的应用[J].中国农村水利水电, 2014,(11):82-85.

[8]刘东, 龚方华, 付强,等.基于博弈论赋权的灌溉用水效率GRA-TOPSIS评价模型[J].农业机械学报, 2017,48(5):218-226.

[9]Shafer G.A Mathematical Theory of Evidence[M].New Jersey: Princeton University Press, 1976.