贵州省马达岭滑坡崩滑形成机制及堆积体稳定性分析

2018-04-13谢明宇张丽波

安全与环境工程 2018年2期

郭　将，曾　超，谢明宇，孟　云，张丽波，刘　晓

(1.中国地质大学(武汉)教育部长江三峡库区地质灾害研究中心，湖北武汉 430074;2.中交第二公路勘察设计研究院有限公司，湖北武汉 430056；3.贵州高速公路集团有限公司，贵州贵阳 550001)

近年来，随着采矿活动的增加，采动滑坡[1]的数量呈递增之势，其危害重大。典型案例[2]如1980年盐池河岩崩，摧毁矿山，死亡284人，损失约2 500万元；1994年重庆武隆鸡冠岭岩崩，伤亡20余人；2009年的鸡尾山滑坡,也造成80余人伤亡。纵观这些滑坡，大部分位于我国的中西部地区，拥有独特的地质条件和采矿环境，崩滑堆积体也为孕育其他次生地质灾害提供了物质来源，如滑坡形成的泥石流或堰塞湖等。因此，深入探讨滑坡崩滑的形成机制以及多种工况条件下崩滑堆积体的稳定性具有重要意义。

马达岭滑坡是一个典型的采动触发的缓倾岩层滑坡，分别于2003年、2006年和2007年发生了3次崩滑，形成了目前的崩滑堆积态势。针对该滑坡，崔文博等[3]通过工程地质条件及动力特征研究,探讨了马达岭滑坡的发生机理与运动特征；王玉川[4]在室内岩石力学试验的基础上，运用离散元法分析了马达岭滑坡的演化破坏机制；赵建军等[5]针对采空区变形采用离散元法数值模拟，分析了滑坡的形成机制；肖建国[6]通过研究马达岭滑坡的形成与运动过程，运用工程地质类比法预测了接娘坪的变形与运动过程；赵建军等[7]采用物理模拟方法，研究了采动滑坡的变形过程，并总结了采动滑坡破坏的地质力学模式；史文兵等[8]在分析斜坡破坏机制的基础上，运用楔形块体原理分析并计算了采动斜坡的稳定性系数。

为了研究马达岭滑坡崩滑堆积体稳定性对在建都匀至香格里拉高速公路的影响，本文在前人研究[3-10]的基础上，通过对滑坡区工程地质特征和变形破坏特征的调查，从地层岩性、岩体结构、软弱夹层、地下水等方面分析了马达岭HP1滑坡崩滑形成的原因及其演化破坏机制，并采用GeoStudio软件[11]包中SEEP/W渗流有限元和SLOPE/W极限平衡法联合求解的方式，模拟计算了在自然状态、降雨状态、地震作用和降雨联合地震作用4种工况条件下滑坡崩滑堆积体的稳定性，分析了降雨强度、降雨持时和地震作用对滑坡崩滑堆积体稳定性的影响。

1　马达岭滑坡的工程地质特征

1. 1　滑坡的基本特征

马达岭滑坡位于贵州省都匀市江州镇富溪村，所在地区位于扬子准地台黔南台陷四级构造单元贵定南北向构造变形区。根据斜坡变形破坏特征，将斜坡区域分为已滑滑坡HP1区域、HP1滑坡堆积体经降雨搬运后的泥石流NSL1区域和滑坡隐患DY208-1区域三个部分，见图1。据调查，2006年连续6天暴雨导致滑坡发生，滑体体积为1.39×106m3，考虑松方系数及下滑过程中对两侧的铲刮作用，最终形成的堆积体体积约为2.1×106m3。

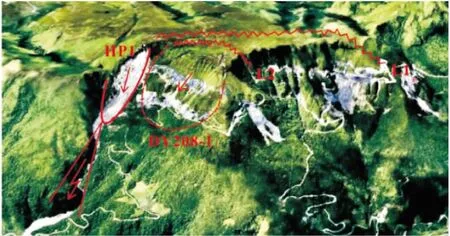
图1　马达岭滑坡航拍图[12]Fig.1　Aerial photo of Madaling landslide[12]

马达岭滑坡为一典型的平缓反倾斜横向坡，上陡下缓似“靴状”(上部坡度约36°、下部坡度约22°)，岩层走向近南北，缓倾向坡内，呈软硬互层结构。坡内煤层开采造成采空区顶板冒落地表塌陷，斜坡受力状态改变，坡顶拉裂形成裂缝，导致斜坡变形破坏严重。

1. 2　滑坡的地层岩性组合

斜坡岩层具有上陡下缓、软硬相间的多元结构特征。斜坡上覆第四纪残坡积土，陡崖下部分布有以砂岩、泥岩为主的崩坡积物，冲沟中为第四纪冲洪积层；斜坡基岩出露地层自上而下分别为细粒石英砂岩、黑色炭质页岩和煤层、灰色中厚层状粗晶生物灰岩夹细粒石英砂岩、细晶灰岩和泥盆系上统高坡场组细晶白云岩。马达岭滑坡典型的地质剖面见图2。

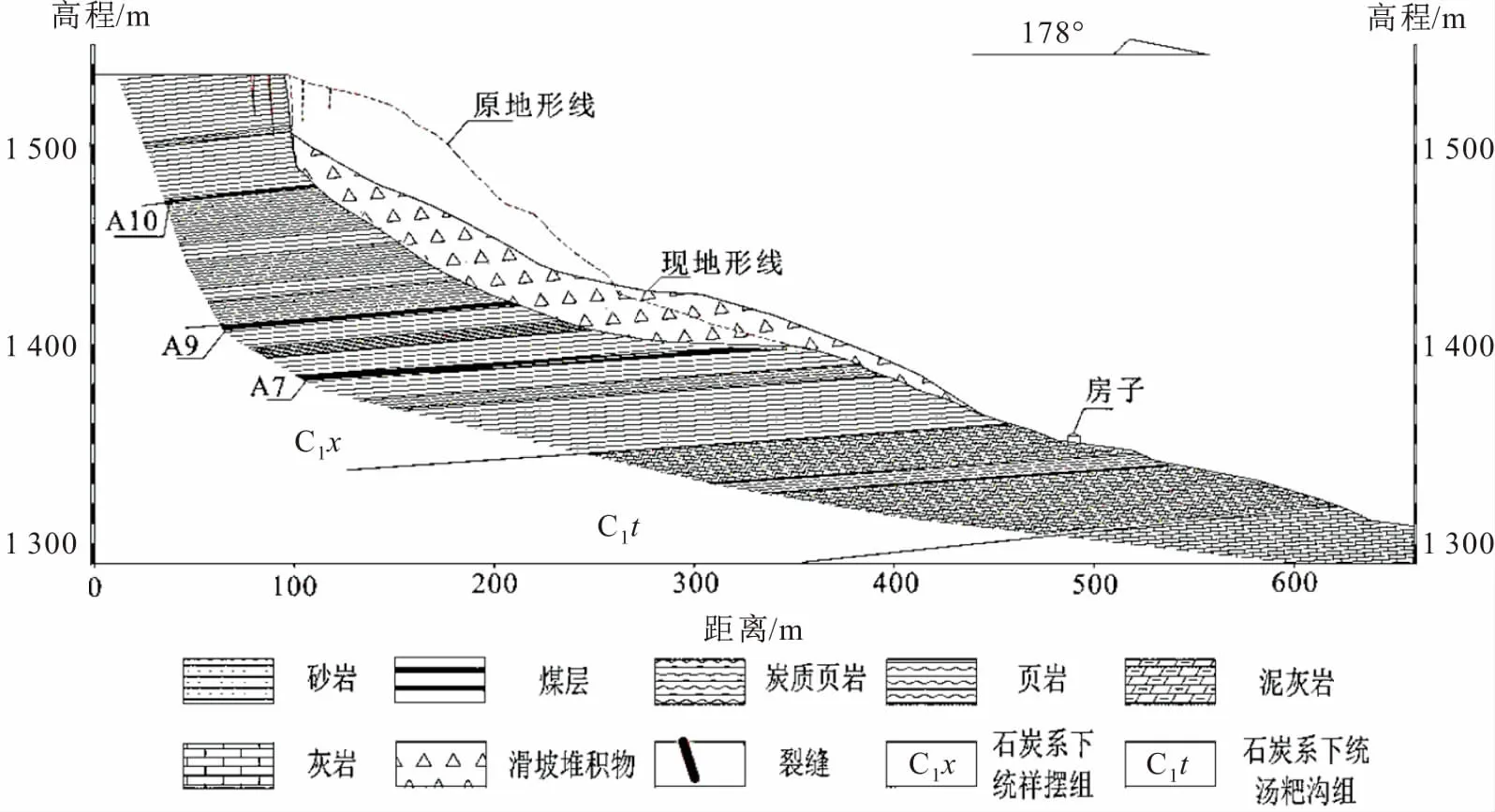
图2　马达岭HP1滑坡的地质剖面图Fig.2　Geological profile of Madaling HP1 landslide

斜坡岩体表面节理裂隙发育、风化严重，表层的第四纪松散堆积物和裂隙的发育为地表水的入渗提供了良好的条件。石英砂岩为硬质岩，其下部为典型的贵州煤系地层岩体，煤系地层中的煤层、炭质页岩为相对软弱层，产状为280°∠15°，具有岩性软、孔隙比大、强度低、易变形的特点，遇水易软化，在上覆砂岩的自重应力下，易发生塑性破坏，对斜坡的稳定性具有控制性作用。

1. 3　滑坡边界及结构面

HP1滑坡滑体边界清晰，平面呈似圈椅状，滑坡后壁下切约40 m，近垂直，砂岩中风化严重，裂隙发育，可见有两组陡倾结构面发育：一组为近EW向的近直立结构面，产状为205°～220°∠80°～86°，另一组为近SN向的陡倾结构面，产状为100°～115°∠76°～82°，受其影响，滑坡西侧边界走向为N22°E、后壁走向为N56°W，见图3。滑坡西侧边界受滑坡下滑中铲刮和冲击作用，有明显的擦痕；滑坡东侧边界受滑坡堆积体影响，边界不清晰。

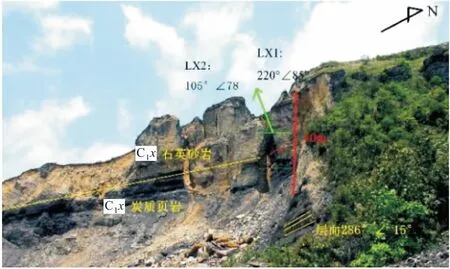
图3　马达岭HP1滑坡后壁[12]Fig.3　Back scrap of Madaling HP1 landslide[12]

在斜坡北高南低的地形地貌条件下，由于大角度相交的两组陡倾节理和岩层层面的切割，滑源区岩体被切割成碎裂状块体，在具备良好的临空条件下，有向S向崩滑的趋势。

1. 4　地下水及降雨

马达岭HP1滑坡被两组陡倾且大角度相交的结构面及沿含煤层的软弱岩层切割，离散型较好，拥有良好的地下水补给、径流和排泄条件。地下水类型主要为基岩裂隙水、碳酸盐夹碎屑岩类岩溶水、纯碳酸盐岩类岩溶水，其次为松散岩类孔隙水。基岩裂隙水主要分布在石炭系下统祥摆组的石英砂岩和炭质页岩及煤层中，其中石英砂岩为含水层，炭质页岩和煤层为相对隔水层；碳酸盐岩类岩溶水分布于石炭系下统汤粑沟组灰岩和泥盆系灰岩、白云岩等碳酸盐岩中，为强含水层。受地形条件影响，地下水主要以大气降水、地表入渗的方式接受补给，在地势低洼地段以泉的形式排泄。

作者认为，连续降水是马达岭滑坡发生的触发因素，也是主导因素。采动前，降雨沿裂隙垂直入渗和顺层面渗透，弱化了岩体的完整性和坚固性，原生结构裂隙扩大；随着坡顶塌陷、后缘裂缝不断延伸，在连续降雨条件下，坡顶沉陷区不断积水，坡顶和坡面的孔隙水压增大，非饱和区减少，加之固液耦合作用，坡脚处的最大剪应力增大。可见，雨水入渗和滑坡变形蠕滑之间产生“共生效应”：地表水入渗对坡体产生的软化作用、静动水压力和扬压力，使软弱层塑性变形加剧，推动坡体向临空面蠕动，而滑面进一步贯通；而滑面的贯通，也促进了水的进一步入渗。

2　马达岭滑坡的演化破坏机制分析

马达岭HP1滑坡分别于2003年、2006年和2007年发生了3个期次的崩滑，其中2006年的滑动形成了目前的主要崩滑堆积状态。本文结合现场调查以及王玉川[4]、赵建军等[5,7]、肖建国[6]的研究成果，将HP1滑坡的演化破坏过程概括为以下几个阶段：

(1) 自然演化阶段：长期自然演化中，受重力控制，斜坡上覆硬质石英砂岩下压，下伏软质炭质页岩和煤层产生塑性变形，向临空方向挤出卸荷；坡顶岩体形成拉应力区，产生拉张裂隙，坡内岩体在卸荷作用下产生卸荷裂隙，且大多追踪构造面发育；斜坡在开采前已经处于稳定状态。

(2) 采空塌陷阶段：采动条件下，上覆岩体受扰动，斜坡内部发生应力重分布；在重力和卸荷作用下，采空区顶板处于悬露状态，生成竖向拉张裂隙和斜向剪切裂隙，开始发生弯曲和冒落，采空区边界形成应力集中区，产生张裂隙，在坡顶将表现为地表裂缝的发育，而在上覆岩层间由于受力和变形不均匀，产生离层裂隙，坡脚部位由于上覆岩层的弯曲挤压作用，产生塑性变形和水平向剪切变形，向临空面发生蠕滑塑性变形；随着采空区范围增大，上覆岩体进行应力和结构的不断调整，坡内岩体在破裂—稳定状态间不断进行循环，其直观结果为坡体变形不断增加、坡顶出现缓慢的沉陷变形、坡体后缘的拉裂缝也不断向下延伸；坡体开裂变形逐渐增大，追踪近东西向深大裂缝成为边坡北侧边界；当采空边界及由采空顶板形成的板梁结构受力达到临界条件后，顶板裂隙快速发育，发生大面积冒落，应力平衡拱形成，坡体再次达到暂稳状态。

(3) 蠕滑贯通阶段：随着采动区的稳定，上覆岩体中的陡倾裂隙终止于斜坡中部软弱岩层，与岩层面构成阶梯状滑移面;阶段状滑移面、后缘深大裂缝和坡脚的剪切带之间的岩层则成为潜在滑面的“关键锁固段”,在降雨作用下，地表水沿后缘深大裂缝入渗，进一步弱化斜坡工程地质条件，使斜坡前缘蠕滑;蠕滑作用使“关键锁固段”应力集中，达到临界状态后锁固段剪断，基本形成完整的滑面。

(4) 破坏失稳阶段：持续的降雨作用下，滑带力学参数劣化，在坡内水体的静动水压力和浮托力作用下，“关键锁固段”剪断，滑体以后缘张裂缝为后边界，A7煤层为剪出口，整体下滑，形成滑坡。

3　马达岭滑坡崩滑堆积体的稳定性及其对高速公路规划线路的影响分析

在马达岭HP1滑坡崩滑的演化过程中，区域地表强烈改造，目前的崩滑堆积体剖面见图2。由于都匀至香格里拉高速公路规划线路距离滑坡前缘较近(见图4)，因此该滑坡崩滑堆积体的稳定与否将对规划线路构成潜在威胁，须定量评估其影响。

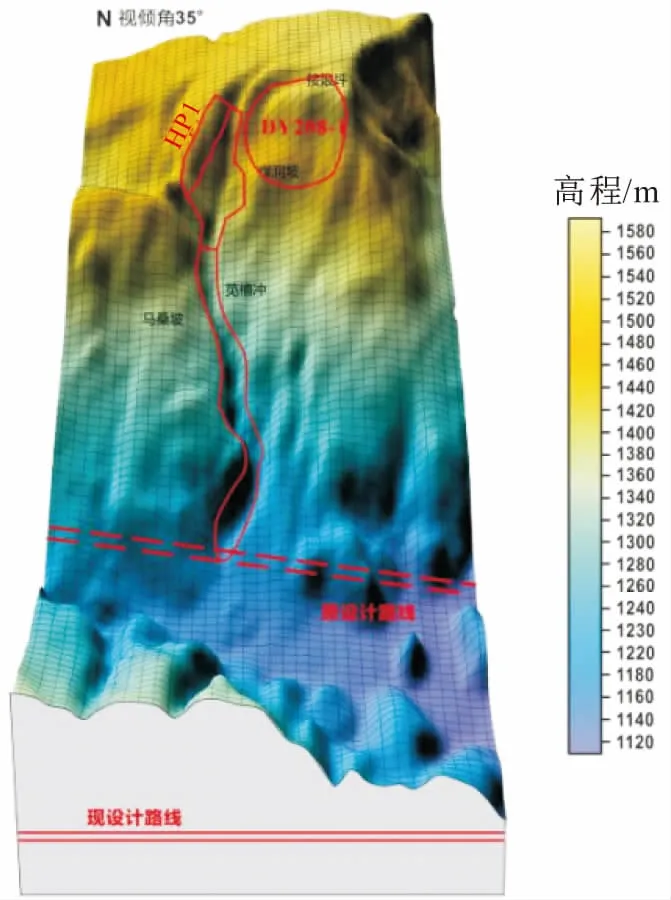
图4　　　　马达岭HP1滑坡崩滑堆积体与都匀至香格里拉高速公路规划线路位置的关系Fig.4　　　　Relationship between the collapse accumulation body of Madaling landslide and the planning route of Duyun-Shangri-La highway

HP1滑坡崩滑堆积体的主要物质成分为松散破碎、风化强烈的砂岩、页岩及煤层，故本文考虑采用非饱和土渗流模型模拟降雨入渗条件下崩滑堆积体的稳定性。非饱和土基质吸力的变化是影响边坡稳定性的重要因素，基质吸力的存在使土体的抗剪强度较高，当降雨渗入土体或者地下水位升高时，基质吸力会逐渐降低，导致土体抗剪强度降低，从而降低边坡的稳定性[13-15]。因此，在马达岭HP1滑坡崩滑堆积体稳定性分析中，是否考虑其基质吸力(或负孔隙水压力)将对评估结果产生较大的影响。

本文以GeoStudio软件为平台，采用SEEP/W渗流有限元模块与SLOPE/W极限平衡分析模块联合求解的方式，对马达岭HP1滑坡崩滑堆积体的稳定性进行了模拟计算与分析，并考虑到该滑坡的稳定性与极端天气和地震作用有关，在稳定性模拟计算中将考虑自然状态、降雨状态、地震作用和降雨联合地震作用4种工况条件。具体计算过程如下：先利用SEEP/W模块对马达岭HP1滑坡进行建模，获得自然状态下HP1滑坡的稳态渗流场;再将其渗流结果导入SLOPE/W模块中进行自然状态下滑坡稳定性分析，并采用拟静力法输入地震加速度，进行滑坡稳定性分析；再次在SEEP/W稳态渗流场中添加降雨边界条件，获得瞬态渗流场并计算其稳定性；最后将瞬态渗流结果导入SLOPE/W模块中并输入地震加速度，进行降雨和地震联合作用下的滑坡稳定性分析。

3. 1　渗流理论

边坡的地下水位线一般为饱和区与非饱和区的分界线，随着降雨的进行，边坡体内的饱和区与非饱和区的范围随之变化。根据质量守恒原理及达西定律，在等热条件下，多维各向异性的非饱和区水分运动的基本方程[16-17]为

(1)

式中:h为全水头；Kx、Ky、Kz为各方向的渗透系数；C(θ)为比水容重，物理意义为压力变化所引起土中含水量的变化，其表达式为

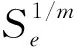
(2)

其中，α、m、n为拟合参数;θs为饱和含水量;θr为残余体积含水量；Se为Van-Genuchen(1980)拟合的水-土特征曲线方程(SWCC)。

由此，渗透函数可表示为

(3)

边界条件[18]如下：

水头边界为

(4)

流量边界为

(5)

式中:r1、r2分别为水头边界和流量边界。

3. 2　计算模型

根据边坡的岩层组合特征及边界条件，本文选取马达岭HP1滑坡主滑面作为计算剖面，采用GeoStudio中的SEEP/W渗流有限元模块建立数值计算模型，考虑到各岩性互层及夹层对滑坡岩体强度的影响，将计算模型简化为如图5所示的结果。模型包含3 505节点、3 084个单元。

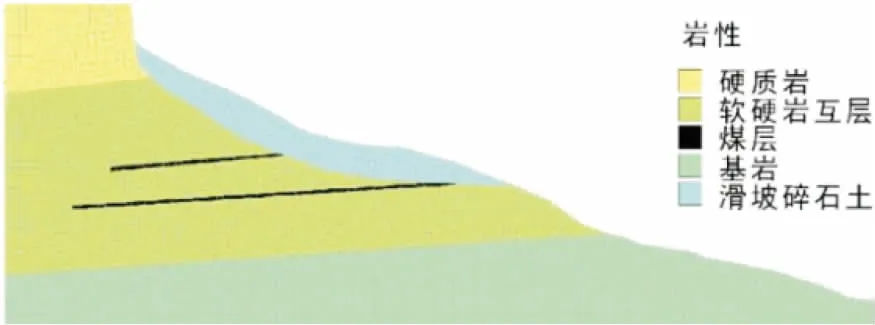
图5　马达岭HP1滑坡的数值计算模型Fig.5　Numerical model of Madaling HP1 landslide

计算模型边界条件约束具有不确定性。初始渗流场分析时边界条件为：模型水头边界、初始斜坡表面零流量边界、降雨入渗随降雨强度不同的Neuman边界。

3. 3　计算参数

降雨条件下的边坡存在饱和区和非饱和区两部分，非饱和区采用Van-Genuchten经验曲线[19]来模拟其渗流情况。本文根据现场调查及室内试验结果，参考已有岩体物理力学参数和类似工程经验，考虑岩体的风化程度及结构面发育情况，将岩体物理力学参数采用折减后的参数，详见表1。

表1　岩体物理力学参数的取值Table 1　Physico-mechanical parameters of rocks

3. 4　数值模拟计算

3.4.1自然状态下滑坡的稳定性计算

本文采用GeoStudio中的SEEP/W模块进行自然状态下马达岭HP1滑坡的渗流场分析，并根据得到的孔隙水压力导入SLOPE/W模块，采用Morgenstern-Price极限平衡法计算得到该滑坡的稳定性系数为1.275。自然状态下马达岭HP1滑坡的渗流场特征见图6。

图6　自然状态下马达岭HP1滑坡的渗流场特征Fig.6　　　　Characteristics of seepage field of the Madaling HP1 landslide under natural state

3.4.2降雨状态下滑坡的稳定性计算

据文献[10]所述，马达岭HP1滑坡所在地区降雨量为1 169 mm/a，夏季占降水总量的44%，且历史最大日降雨量为170.5 mm，考虑降雨强度对坡体暂态和瞬态孔隙水压的影响，现取一天的等强型暴雨降雨量2×10-6m/s(即172 mm/d)为基本值，分别以100 mm/d、120 mm/d，150 mm/d、172 mm/d、200 mm/d、220 mm/d的降雨量为变量，模拟计算了降雨强度和降雨持续时间(以下简称降雨时长)对马达岭HP1滑坡稳定性的影响，其计算结果见图7和图8。

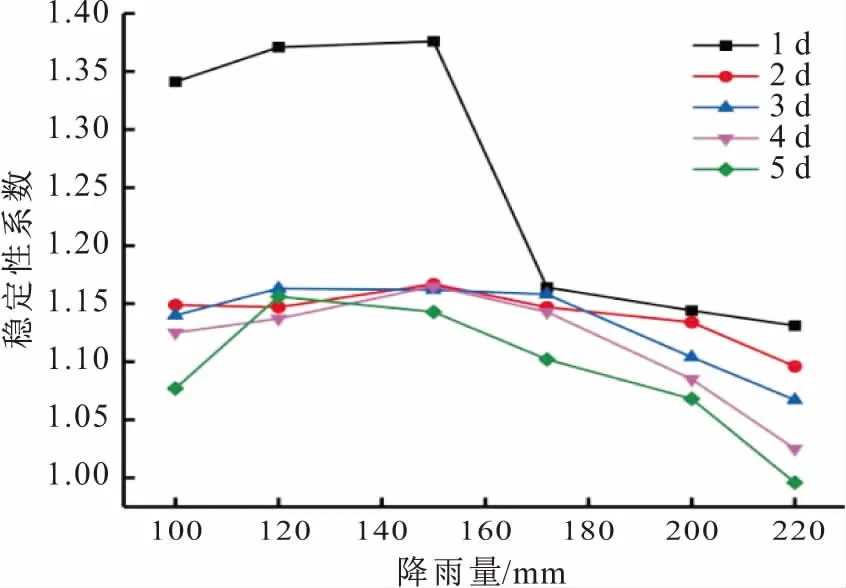
图7　　　　不同降雨强度下马达岭HP1滑坡的稳定性系数变化曲线Fig.7　　　　Variation curves of the stability coefficient of Mada- ling HP1 landslide at different rainfall intensity

不同降雨强度下，坡体暂态孔隙水压分布不同，从而对滑坡的稳定性影响不同。

由图7可见，随着平均日降雨强度的增加，马达岭HP1滑坡的稳定性系数总体呈减小的趋势。当降雨强度为100～150 mm时，该滑坡的稳定性系数有增高的趋势；当降雨强度大于150 mm后，该滑坡的稳定性系数降低。以上结果可以理解为：当降雨强度较小，滑坡土体渗透系数较大时，雨水入渗较快，斜坡浅层难以达到饱和，因而土体基质吸力较大；当降雨强度大于渗透系数时，雨水垂直渗透慢，一部分在坡表形成积水或径流，使斜坡浅层易达到饱和，土体基质吸力降低，抗剪强度也减弱，导致该滑坡的稳定性系数持续降低。

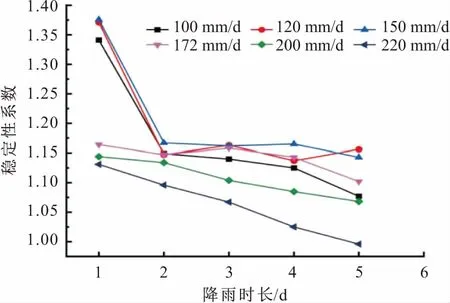
图8　不同降雨持续时间下滑坡稳定性变化曲线Fig.8　　　　Variation curves of the stability coefficient of Mada- ling HP1 landslide at different rainfall duration

由图8可见，在降雨强度不变的情况下，随着降雨持续时间的增加，马达岭HP1滑坡的稳定性系数将不断降低。在低降雨强度下，降雨时长超过2 d时，该滑坡稳定性系数将逐渐趋于稳定；而在降雨强度大于172 mm/d时，降雨时长将会引起该滑坡稳定性系数的显著降低；当降雨强度为220 mm/d、降雨时长超过5 d时，该滑坡将处于不稳定状态。此外，值得注意的是，当降雨时长为1 d时，小于150 mm和大于172 mm的不同降雨强度下该滑坡稳定性的差别较大；而降雨时长为2 d及以上时，不同降雨强度下该滑坡的稳定性基本相差不大。分析认为，表1中采用堆积碎石土的渗透系数介于150～172 mm/d之间，故降雨强度对该滑坡稳定性的影响较大；随着降雨时长的增加(超过2 d)，斜坡浅层基本达到饱和，故降雨强度与土体渗透系数的关系对该滑坡稳定性的影响减小，不同降雨强度下该滑坡稳定性系数的差别变小。

3.4.3地震作用下滑坡的稳定性计算

依据规范[20-21]，将地震视为惯性力，并按是否考虑竖向地震力(Fv)为划分依据，采用拟静力法进行滑坡的稳定性计算。据最新地震加速度区划图[22]，马达岭滑坡所在区域地震动峰值加速度为0.05g，相应地震基本烈度为Ⅵ，采用附加地震水平加速度为0.05g，模拟计算考虑地震作用下马达岭HP1滑坡的稳定性，其计算结果见表2。

表2　多种工况下马达岭HP1滑坡的稳定性系数Table 2　　　　Stability factors of Madaling HP1 landslide under various conditions

注：1.Fh为水平向地震惯性力，即Fh=αhξWiαi/g(其中，αh为水平向设计的地震加速度;ξ为地震效应折减系数，取0.25;Wi为质点i的重力;αi为质点的动态分布系数;g为重力加速度)；Fv为竖向地震惯性力，在遇合系数设为1/2的条件下，取水平向地震惯性力的2/3，即Fv=Fh×1/2×2/3[23]。2.降雨状态指降雨量为2×10-6m/s、降雨持续时间为24 h的情况。

3.4.4降雨联合地震作用下滑坡的稳定性计算

本文综合实际情况，考虑降雨量为2×10-6m/s、降雨时长为24 h的情况下，拟合最大地震力进行滑坡的稳定性计算，其瞬态渗流场见图9，地震联合降雨作用下的马达岭HP1滑坡的稳定性计算结果见表2。

通过对比自然状态和降雨状态下马达岭HP1滑坡的渗流特征(见图6和图9)可知，降雨状态(指降雨强度为172 mm/d、降雨时长为24 h的情况)下，非饱和区将出现暂态饱和区，其分布在该滑坡堆积碎石土与边坡岩体的接触部分，且以地表径流方式排泄，符合实际情况。分析认为，由于堆积碎石土带的饱和渗透系数远大于边坡岩性，而暂态饱和区的形成也由于渗透系数会有滞后效应，所以暂态饱和区在24 h后的分布位置见图9。

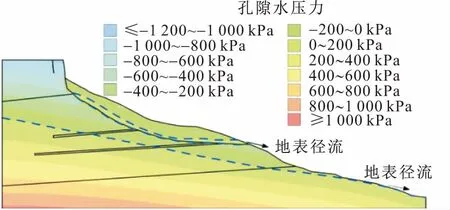
图9　降雨状态下马达岭HP1滑坡的渗流场特征Fig.9　　　　Characteristics of seepage field of Madaling HP1 landslide under rainfall condition

由多种工况下马达岭HP1滑坡的稳定性系数对比分析可知，降雨联合地震作用对该滑坡稳定性的影响比其中任何单一因素对滑坡稳定性的影响要大。此外，地震作用下，该滑坡的稳定性处于基本稳定状态；在单一施加地震力情况下，只施加水平地震力和同时考虑竖向地震力对该滑坡的稳定性系数基本没有差别；而在降雨状态下，考虑竖向地震力则对该滑坡的稳定性系数(1.093)有轻微影响，但结果基本相当，表明竖向地震力对该滑坡的稳定性系数基本没有影响。但需要注意的是，暴雨联合地震作用的情形为该滑坡所面临的最恶劣条件，计算得到的稳定性系数对该滑坡的稳定性评价具有一定的参考价值。

3. 5　马达岭滑坡稳定性对高速公路规划线路的影响

都匀至香格里拉高速公路原规划线路为路桥方案，距离马达岭滑坡前缘较近，鉴于该滑坡的安全储备不足，将对原规划线路方案构成较大的威胁，因此在后期施工图设计阶段，采取了积极规避的策略，最终选线在马达岭滑坡滑体以南2 km，并以山体隧道的方式穿越潜在影响区。

4　结论与建议

本文通过对马达岭滑坡的工程地质条件、形成机理分析，并在GeoStudio软件平台考虑自然状态、降雨状态、地震作用、降雨联合地震作用4种工况下模拟计算分析了马达岭滑坡的稳定性，得出以下结论：

(1) 马达岭滑坡是典型的以采矿为诱发条件，降雨为直接触发条件的具有时效变形特点的灾害型滑坡。滑动后的滑坡堆积体在自然状态下较为稳定，在强降雨条件下将处于基本稳定至不稳定状态。

(2) 在降雨强度和降雨时长对马达岭滑坡稳定性影响的数值模拟计算中，降雨强度和降雨时长都是导致马达岭滑坡稳定性系数降低的重要因素。随着降雨强度的升高，马达岭滑坡的稳定性系数总体呈减小趋势，具体表现为稳定性系数先升高后呈降低趋势。此外，随着降雨时长的增加，降雨强度与土体渗透系数的关系对马达岭滑坡稳定性的影响减小，滑坡的稳定性系数持续降低。

(3) 降雨联合地震作用对马达岭滑坡的稳定性影响比其中任何单一因素的影响要大，但竖向地震力对该滑坡稳定性的影响远小于水平地震力。稳定性系数计算结果显示，马达岭滑坡处于基本稳定状态。

(4) 本文在对降雨状态影响滑坡稳定性系数的模拟计算中，考虑到降雨情况较为随机，故未考虑降雨类型对滑坡稳定性的影响，均假定降雨类型为等强度降雨；其次降雨强度与降雨时长可能存在一定的相关性，其对滑坡稳定性系数的影响是相互的，这是今后需要进一步研究的方向。

(5) 鉴于马达岭滑坡的安全储备不足，都匀至香格里拉高速公路在马达岭滑坡区段采取积极规避的策略是合理的。

参考文献：

[1] 汤伏全.采动滑坡的机理分析[J].西安科技大学学报,1989(3):32-36.

[2] 李腾飞,李晓,苑伟娜,等.地下采矿诱发山体崩滑地质灾害研究现状与展望[J].工程地质学报,2011,19(6):831-838.

[3] 崔文博,向喜琼,王晗旭.贵州都匀马达岭滑坡运动特征研究[J].地下水,2013.35(3):145-147,153.

[4] 王玉川.缓倾煤层采空区上覆山体变形破坏机制及稳定性研究[D].成都：成都理工大学,2013.

[5] 赵建军,肖建国,向喜琼,等.缓倾煤层采空区滑坡形成机制数值模拟研究[J].煤炭学报,2014,39(3)：424-429.

[6] 肖建国.缓倾采空区斜坡变形破坏及运动特征研究[D].成都：成都理工大学,2014.

[7] 赵建军,马运韬,兰志勇，等.平缓反倾采动滑坡形成的地质力学模式研究——以贵州省马达岭滑坡为例[J].岩石力学与工程学报,2016(11)：2217-2224.

[8] 史文兵,黄润秋,赵建军.基于组合楔形体原理的采动坡体稳定性研究[J].工程地质学报,2014,22(6)：1168-1175.