一种引导测试向量自动生成广义折叠集的方法
2018-04-12詹文法程一飞吴海峰江健生
詹文法 程一飞 吴海峰 江健生
(安庆师范大学计算机与信息学院, 安庆 246133)
随着集成电路技术的发展,测试成本已成为影响集成电路成本的主要问题之一,最有效的解决方法是通过压缩测试数据量达到减少测试成本的目的.按是否同时压缩原始测试数据的长度或宽度,可以将测试数据压缩方法分为一维压缩和二维压缩.一维压缩仅单一压缩测试数据的长度或宽度.压缩测试数据长度的代表性方法包括基于LFSR的压缩技术[1-2]和基于编码的压缩技术[4-11]等.基于LFSR的压缩技术优点是可以采用种子编码整个测试向量,但LFSR种子长度与单个测试向量中最多确定位有关,即受最坏环境影响;基于编码的压缩技术优点是不需要提供被测电路的内部结构,能够保护知识产权,缺点是无法解决测试数据与自动测试设备之间的同步问题.压缩测试集宽度的代表性方法有测试紧缩技术[12],该技术的优点是不增加任何硬件成本,缺点是难以覆盖被测电路中的非固定性故障.二维压缩同时压缩测试集的长度和宽度,代表性的有基于折叠集和广义折叠集的测试数据压缩技术[13-14].
从压缩效果上看,二维测试压缩能有效地组合折叠计数器、扭环计数器以及LFSR编码技术,其压缩效果为所有同类技术中最优.然而,传统的二维压缩技术未探讨测试集内部测试向量之间的相关性,其压缩效果不好.本文提出了一种引导自动测试向量生成的广义折叠技术,即根据信号线的确定值计算对应的原始输入,在测试生成时嵌入广义折叠技术,以确保按照广义折叠规律生成广义折叠集.
1 广义折叠技术
广义折叠集的基本思想是将整个测试集的直接存储转换成广义折叠种子和对应折叠距离的间接存储.不失一般性,设由t个不同向量组成原始测试数据,将这t个向量嵌入到n个广义折叠集中,这样对原始测试集的存储就转换成对n个广义折叠集的存储.进一步可将整个原始测试集的存储转换成对n个广义折叠种子和对应折叠距离的存储,其中t≫n[15].
构成广义折叠集的向量之间无相关性,限制了广义折叠集的压缩效果,中间产生了很多对测试覆盖率无关的测试向量,增加了测试时间和测试功耗.
2 测试向量生成策略
2.1 准确影响范围技术
传统的自动测试向量生成工具是基于故障点产生测试向量的,测试向量之间无相关性,难以将其嵌入到折叠集等固定翻转规律的单一序列中,因而很难达到最优压缩效果.传统算法中通过输入核来判断一个信号线的影响区域,无法准确识别一个有确定值的信号线影响的输入范围.一个触发器的输入核可能有很多输入,在测试向量的产生过程中,只有一部分会被置为确定值.因此,准确识别能够被该触发器影响的输入对后面的压缩工作具有很大的指导意义.
SCOAP是ATPG过程中广泛应用的一种可测性度量方法.但是它只单独分析各个门电路,不能在全局上进行测量.本文提出了一种新的测度,将每一个信号线取确定值可能影响的基本输入(PI)或伪基本输入(PPI)的集合记录下来,在回溯的过程中进行选择.
信号线l的可控性Ti(l)是使l赋值为i(i∈{0,1})时从l到PPI所有门电路的可控性之和,如果存在多条通路,则取最小值.令Ci(l)表示使l赋值为i时从l到PPI最小通路的距离,记为Ci(l)=|Ti(l)|.
如果l的输入为PI或者PPI,用l(0)和l(1)分别代表信号线l被赋值为0和1,则
T1(l)={l(1)},T0(l)={l(0)}
(1)
C1(l)=C0(l)=1
(2)
对于一个与门来说,假设其输入值为A和B,则
T1(l)=T1(A)∪T1(B)
(3)
C1(l)=C1(A)+C1B+ΔC
(4)
式中,ΔC为门的级数,默认值为1.
区分PI和PPI是为了向尽量少的PPI方向回溯.如果对于输入端都是PI的情况,C取值为10,作为一个惩罚值.
类似地,与门之间存在如下关系:
(5)
(6)
使一个与门的输出值为0,只需要任一个输入值为0.如果存在多种选择,则优先选择最小代价进行回溯.
对于一个输入值为A或B的或门,有
T0(l)=T0(A)∪T0(B)
(7)
C0(l)=C0(A)+C0(B)+ΔC
(8)
(9)
(10)
对于一个输入值为A的非门,有
T1(B)=T0(A),C1(B)=|T(B)|
(11)
T0(B)=T1(A),C0(B)=|T0(B)|
(12)
对于一个多扇出信号线s,其扇出端值分别为B1,B2,…,Bk,则
Ci(Bj)=Ci(s)
(13)
与非门和或非门的计算情况与上面类似,可以按照与门、非门和或门直接复合.
对于一个确定的故障,检测时不仅需要将其激活,还需要把故障效应传递到原始输出.因此,需要定义每个信号线的可观测性.
与可控制性类似,可观测性Qi(l)定义为使l赋值为i(i∈{0,1})时从PPO到l所有门电路的可控制性之和,如果存在多条通路,则取最小值.令Oi(l) 表示使l赋值为i时从PPO到l最小通路的距离,记为Oi(l)=|Qi(l)|.
对于电路的原始输入端M,有
Q(M)=Ø,O(M)=0
(14)
对于非门,令输入值为A,输出值为B,则
Q(A)=Q(B)
(15)
O(A)=|Q(A)|
(16)
对于二输入与门,输入值为A和B,输出值为p,则
Q(A)=Q(p)∪T1(B)
(17)
O(A)=|Q(A)|
(18)
对于二输入或门,输入值为A和B,输出值为p,则
Q(A)=Q(p)∪T0(B)
(19)
O(A)=|Q(A)|
(20)
对于扇出s,设B1,B2,…,Bk为多扇出分支值,则
O(s)=min(O(B1),O(B2),…,O(Bk))
(21)
由此可得一个故障的原始输入.在ATPG产生测试向量的过程中,选择性地调整确定位位置,使产生的测试向量符合广义折叠规律.
2.2 故障合并策略
在2个故障生成测试向量过程中,可以按照如下3个原则来执行:
① 如果2个故障没有相同的结构输入核,那么它们肯定是可以合并的,基于这2个故障产生一个测试向量;
② 如果2个故障的结构输入核有交叉,其影响范围没有交叉,可以基于这2个向量产生一个测试向量;
③ 在其他情况下,理论上不能判断这2个故障是否可以直接合并成一个测试向量,需要通过量化影响范围指标来判断其交叉程度,优先选取影响范围交叉程度小的故障进行测试.
2.3 向量生成顺序
首先按照测试向量的合并策略,将基于同一个测试向量测试的难测故障个数分组,选择可以合并的难测故障数最多的2组故障,产生2个测试向量.与折叠集类似,由这2个测试向量计算对应的广义折叠集,根据得到的广义折叠集中的测试向量进行故障模拟,检查该广义折叠集所能测试的所有故障.对剩下的难测故障再次分组,得到另一完整广义折叠集.以此类推,直到故障覆盖率达到100%,最终得到若干个确定的广义折叠集.
3 综合过程
通过随机测试将故障分成易测故障和难测故障.难测故障采用2.2节的故障合并策略,按照同一个测试向量测试的难测故障个数分组,选择可以合并故障数最多的2组故障,采用较为准确的影响范围技术来判断每个信号线在回退过程中产生影响的原始输入,指导测试向量的生成过程,产生对应的2个测试向量.与折叠集类似,由这2个测试向量来计算广义折叠集,根据得到的广义折叠集中的测试向量进行故障模拟,检查该广义折叠集所能测试的所有故障.对剩下的故障再次分组,得到另一完整广义折叠集.以此类推,直到故障覆盖率达到100%,最终得到若干个确定的广义折叠集.总体过程见图1.
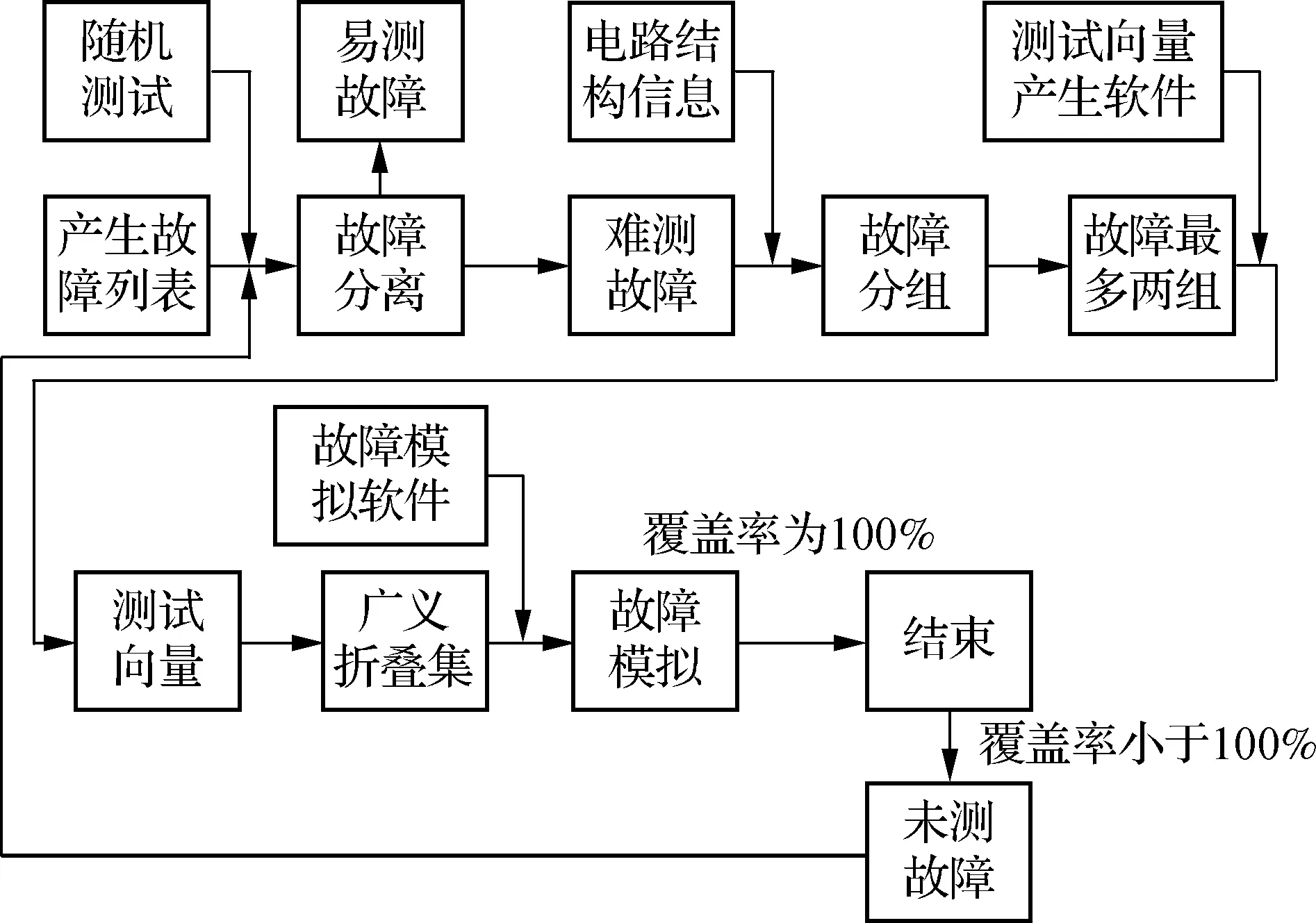
图1 按照广义折叠规律生成的自动测试向量生成算法 技术路线
广义折叠集不同的翻转规律需要配置不同的解压电路,即翻转规律的个数直接决定着硬件的开销.因此,在实际应用时,需要在硬件开销和压缩效果之间权衡,而不仅仅只考虑压缩效果.
4 实验结果
下面通过实验结果来验证ATPG引导后广义折叠技术的压缩效果.选用ISCAS 89标准电路中规模较大的6个时序电路,在随机模式下运行1×104个时钟周期以剔除易测故障.对于剩下的难测故障,运用atalanta等ATPG工具生成确定位最少的硬故障测试集. 在同等情况下,对比本文方法与传统广义折叠技术的压缩效果,结果见表1.
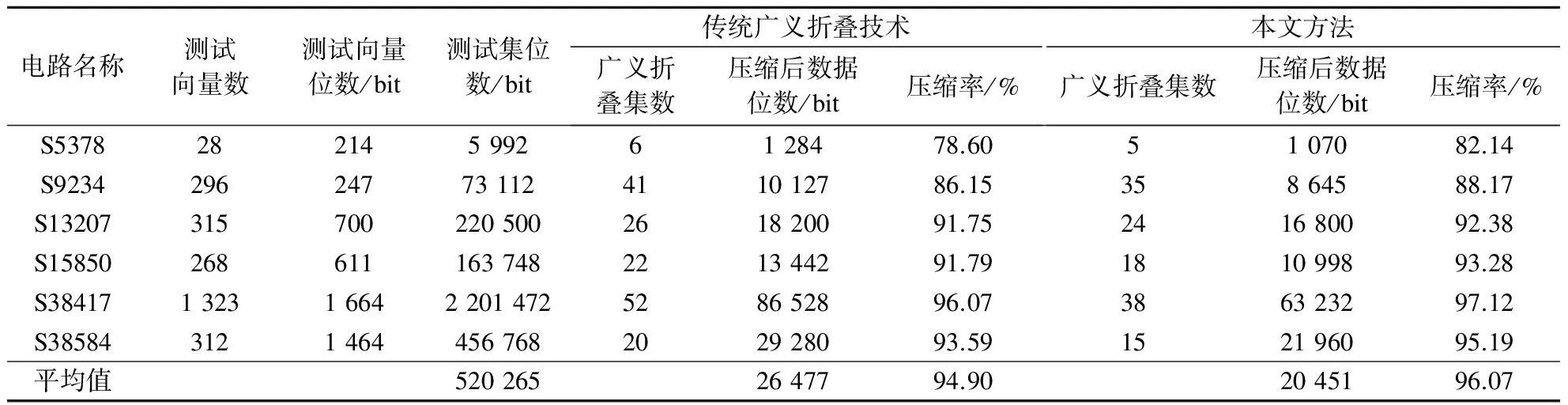
表1 采用ISCAS 89标准电路和硬故障测试集时2种方法的压缩效果比较
由表1可知,对每个标准电路,本文方法的压缩效果明显优于传统广义折叠技术.针对6个标准电路,本文方法的压缩率较传统广义折叠技术平均提高1.17%.这一结果是在未增加硬件开销的情况下得到的,如果增加硬件开销,压缩率提高值还可以进一步增大.随着电路规模的增加,本文方法的压缩率逐渐增大.究其原因在于,电路规模越大,测试向量数越多,嵌入到广义折叠集的概率越大,因而压缩效果也越好.当前实际中的集成电路规模远远高于ISCAS89标准电路,因此,本文方法的优势更为明显.
为了进一步验证本文方法的效果,将其与国内外其他成熟方案在同等实验环境下进行比较.实验中采用ISCAS 89标准电路和Mintest测试集.采用本文方法时,选用难测故障数最多的2个测试向量,使用准确影响范围技术调整测试向量的无关位,并构建ATPG引导的广义折叠集,分析其所测故障数.对剩下的难测故障循环使用该方法,直到故障覆盖率达到100%,从而得到若干个广义折叠集的存储位数.
表2给出了9种方法的压缩率.由图可知本文方法的压缩效果最优.对于ISCAS 89标准电路的6个时序电路,本文方法的压缩率较Golomb码、FDR码、VIHC码、交替连续码、EFDR码、IRIN码、LODP码分别提高22.45%,17.01%,14.40%, 13.92%,11.91%,8.73%,11.33%.6个时序电路中,4个电路采用本文方法时压缩效果最好,压缩率为61%~77%,从而证明了本文方法的稳定性.
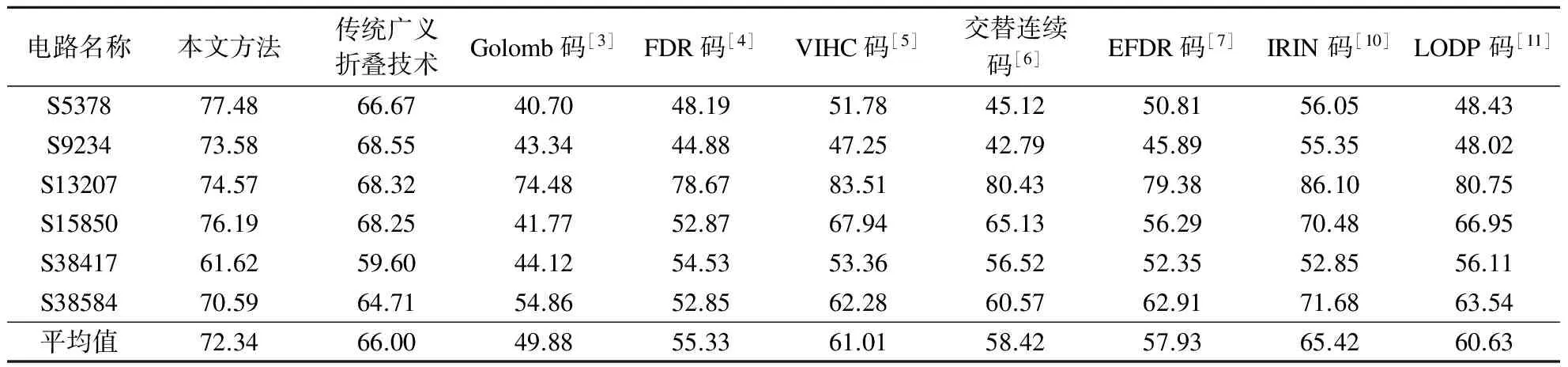
表2 采用ISCAS 89标准电路和Mintest测试集时9种方法的压缩率结果比较 %
5 结论
1) 提出了一种引导自动测试向量生成的广义折叠技术.该技术根据信号线的确定值计算对应的原始输入,在测试生成时嵌入广义折叠技术,确保按广义折叠规律生成广义折叠集.将原始测试数据的直接存储转换成对广义折叠集的种子和折叠距离的间接存储.
2) 相对于传统的二维压缩方法,本文方法可以嵌入更多的测试向量,减少了无用测试向量的产生.实验结果显示,本文方法具有较少的存储位数,被测电路规模越大,优势越明显.
3) 将本文方法与LFSR编码、输入精减、扫描链重排序技术结合使用可进一步提高压缩效果.
参考文献(References)
[1] 梁华国, 刘军, 蒋翠云, 等. 约束输入精简的多扫描链BIST方案[J]. 计算机辅助设计与图形学学报, 2007, 19(3): 371-375 DOI:10.3321/j.issn:1003-9775.2007.03.018.
Liang Huaguo, Liu Jun, Jiang Cuiyun, et al. Constraint input reduction BIST scheme for multiple scan chains[J].JournalofComputerAidedDesign&ComputerGraphics, 2007,19(3): 371-375. DOI:10.3321/j.issn:1003-9775.2007.03.018.(in Chinese)
[2] Xiang D, Chen M J, Fujiwara H. Using weighted scan enable signals to improve test effectiveness of scan-based BIST[J].IEEETransactionsonComputers, 2007,56(12): 1619-1628.
[3] Chandra A, Chakrabarty K. System-on-a-chip test-data compression and decompression architectures based on Golomb codes[J].IEEETransactionsonComputer-AidedDesignofIntegratedCircuitsandSystems, 2001,20(3): 355-368.
[4] Chandra A, Chakrabarty K. Test data compression and test resource partitioning for system-on-a-chip using frequency-directed run-length (FDR) codes[J].IEEETransactionsonComputers, 2003,52(8): 1076-1088. DOI:10.1109/tc.2003.1223641.
[5] Gonciari P T, Al-Hashimi B M, Nicolici N. Variable-length input huffman coding for system-on-a-chip test[J].IEEETransactionsonComputer-AidedDesignofIntegratedCircuitsandSystems, 2003,22(6): 783-796. DOI:10.1109/tcad.2003.811451.
[6] 梁华国, 蒋翠云. 基于交替与连续长度码的有效测试数据压缩和解压[J]. 计算机学报, 2004, 27(4): 548-554. DOI:10.3321/j.issn:0254-4164.2004.04.015.
Liang Huaguo, Jiang Cuiyun. Efficient test data compression and decompression based on alternation and run length codes[J].ChineseJournalofComputers, 2004,27(4): 548-554. DOI:10.3321/j.issn:0254-4164.2004.04.015.(in Chinese)
[7] El-Maleh A H. Test data compression for system-on-a-chip using extended frequency-directed run-length code[J].IETComputers&DigitalTechniques, 2008,2(3): 155-163. DOI:10.1049/iet-cdt:20070028.
[8] 詹文法, 梁华国, 时峰, 等.混合定变长码的测试数据压缩方案[J]. 计算机学报, 2008, 31(10): 1826-1834. DOI:10.3321/j.issn:0254-4164.2008.10.017.
Zhan Wenfa, Liang Huaguo, Shi Feng, et al. A test data compression scheme based on mixed fixed and variable length coding[J].ChineseJournalofComputers, 2008,31(10): 1826-1834. DOI:10.3321/j.issn:0254-4164.2008.10.017.(in Chinese)
[9] 邝继顺, 周颖波, 蔡烁. 一种用于测试数据压缩的自适应EFDR编码方法[J]. 电子与信息学报, 2015, 37(10): 2529-2535. DOI:10.11999/JEIT150177.
Kuang Jishun, Zhou Yingbo, Cai Shuo. Adaptive EFDR coding method for test data compression[J].JournalofElectronics&InformationTechnology, 2015,37(10): 2529-2535. DOI:10.11999/JEIT150177.(in Chinese)
[10] 詹文法, 梁华国, 程一飞, 等. 利用整数存储无理数的测试数据编码压缩方法[J]. 计算机辅助设计与图形学学报, 2016, 28(9): 1605-1612. DOI:10.3969/j.issn.1003-9775.2016.09.025.
Zhan Wenfa, Liang Huaguo, Cheng Yifei, et al. Test data compression coding-based scheme storing integers represented for irrational numbers[J].JournalofComputer-AidedDesign&ComputerGraphics, 2016,28(9): 1605-1612. DOI:10.3969/j.issn.1003-9775.2016.09.025.(in Chinese)
[11] 吴琼, 黄丽. 基于逻辑运算的折半划分测试数据压缩方法[J]. 系统仿真学报, 2015, 27(6): 1324-1328.
Wu Qiong, Huang Li. Test data compression based on logical operational dimidiate partition[J].JournalofSystemSimulation. 2015,27(6): 1324-1328.
[12] El-Maleh A H, Khursheed S S, Sait S M. Efficient static compaction techniques for sequential circuits based on reverse-order restoration and test relaxation[J].IEEETransactionsonComputer-AidedDesignofIntegratedCircuitsandSystems, 2006,25(11): 2556-2564. DOI:10.1109/ats.2005.53.
[13] Liang H G,Hellebrand S,Wunderlich H J. Twodimensional test data compression for scan-based deterministic BIST [J].JournalofElectronicTesting:TheoryandApplications, 2002,18(2): 159-170.
[14] 周彬, 叶以正, 李兆麟. 基于二维测试数据压缩的BIST方案[J]. 计算机辅助设计与图形学学报. 2009, 21(4):481-486,492.
Zhou Bin, Ye Yizheng, Li Zhaolin. BIST scheme based on two-dimensional test data compression[J].JournalofComputer-AidedDesign&ComputerGraphics, 2009,21(4): 481-486,492. (in Chinese)
[15] 詹文法, 吴琼, 程一飞, 等. 嵌入广义折叠技术的集成电路测试数据压缩方案[J]. 计算机辅助设计与图形学学报, 2017, 29(8):1542-1548.
Zhan Wenfa, Wu Qiong, Cheng Yifei, et al. Integrated circuit test data compression scheme built-in generalized folding technology [J].JournalofComputer-AidedDesign&ComputerGraphics, 2017,29(8):1542-1548.(in Chinese)
