组合导航系统中异步多传感器信息融合算法

朱倚娴　程向红　周　玲,2　刘　全

(1东南大学微惯性仪表与先进导航技术教育部重点实验室， 南京 210096)(2运城学院物理与电子工程系， 运城 044000)

为提高导航系统定位精度和容错性能，多传感器组合导航是目前最常采用的有效策略.实现多传感器信息融合的Kalman滤波分为集中式和分布式2种结构.1988年Carlson[1]提出的联邦滤波器作为最具代表性的分布式融合算法，设计灵活、计算量小、容错性能好，被广泛应用于组合导航系统中.多传感器的同步数据采集通过时间同步装置[2-3]实现.在现有的多传感器信息融合研究[4-6]中，大多假设各个导航传感器同步地将数据传递给融合中心.然而，在实际系统中，由于信号变化速率相差较大、检测装置采样周期不同等原因使各个传感器的采样速率不尽相同[7]，且由于传感器固有延迟和通信延迟的不同[8]，使融合中心接收到的数据也不同步.因此，研究针对异步多传感器的信息融合算法对提高组合导航系统定位精度具有重要意义.

赫飞等[9]针对SINS/GPS/捷联星光跟踪仪/高度表组合导航系统各传感器采样率不同的问题，提出了基于状态方程多尺度变换的信息融合算法，将最高采样率下的系统状态方程分解到不同的尺度上，得到各尺度上的状态方程及对应的量测方程.刘磊等[10]利用数据块分析技术和小波变换技术，将状态块向量、量测块向量在粗尺度上分解，并在不同尺度上进行相应的Kalman滤波，得到各尺度上平滑信息的最优估计值，最终利用异步贯序滤波建立基于全局的最优估计值，但该方法要求不同传感器间的采样率必须为2的整数倍.此外上述文献均针对多传感器采样率不同的问题提出了解决方案，但未考虑传感器量测延迟，即数据不同步问题.Safari等[11]针对多传感器异步量测问题，提出一种基于神经网络的信息融合策略，建立基于状态分块的系统模型，并利用神经网络融合各子滤波器的状态估计值.Yang等[12]提出基于UKF的异步数据融合算法，通过检测每个融合期内无线传感器网络的量测值，建立基于时间序列的伪量测方程.Lin等[13]针对含丢包的异步量测问题，利用射影理论推导线性最小方差意义下的最优局部状态估计值，并在此基础上计算局部状态估计误差间的协方差矩阵，最终通过矩阵加权算法得到分布式最优融合状态估计值.刘建业等[14]考虑组合导航系统中量测不等间隔频率输出和量测信息滞后的问题，设计了非等间隔Kalman滤波算法，利用数组记录某一时刻的惯性导航系统(inertial navigation system, INS)状态信息，当对应时刻的合成孔径雷达 (synthetic aperture radar, SAR)量测信息到达时，将其与数组中信息进行融合，再利用Kalman滤波时间更新递推得到当前时刻的状态估计值.

本文针对组合导航系统中多个传感器采样频率不同且存在量测滞后的问题，提出了一种基于多尺度数据分块的组合导航信息融合算法.建立最高采样率下(即最细尺度上)的系统模型，通过状态和观测的分块与扩维，得到多尺度系统模型.利用各尺度上的观测信息分别进行Kalman滤波，经数据融合最终得到基于全局的状态估计值.通过仿真，验证了本文所提信息融合算法可有效提高异步多传感器组合导航系统的定位精度.

1　异步多传感器组合导航系统

1.1　系统描述

设有N个导航传感器(i=1,2,…,N)以不同采样率Si进行观测，且彼此间的采样是异步的，采样率间的关系满足

Sj+1=njSj1≤j≤N-1

(1)

式中，nj为已知正整数.

根据多尺度理论，i(i=1,2,…,N)既表示传感器，也表示尺度.具有最低采样率S1的第i=1个传感器对应于最粗尺度，具有最高采样率SN的第i=N个传感器对应于最细尺度，传感器i=2,3,…,N-1的采样率介于两者之间，依次升高.在最高采样率下(即最细尺度上)建立状态方程，多传感器组合导航系统可描述为

x(N,k+1)=Φ(N,k)x(N,k)+w(N,k)

(2)

z(i,k)=H(i,k)x(i,k)+v(i,k)
i=1,2,…,N-1

(3)

式中，x(N,k)∈Rn×l为最细尺度上k时刻的状态变量；Φ(N,k)为系统一步转移矩阵；系统噪声w(N,k)∈Rn×l为零均值高斯白噪声,Q(N) 为其协方差；z(i,k)∈Rqi×l(qi≤n)为第i个传感器在采样率Si下获得的第k个观测值；H(i,k)∈Rqi×n为观测矩阵；观测噪声v(i,k)∈Rqi×l为零均值高斯白噪声，其协方差为R(i)，且不同采样率下的观测噪声互不相关.初始状态向量x(N,0)为一随机变量，且假设x(N,0)，w(N,k)和v(i,k)彼此间统计独立.

为更清晰地表达各传感器、尺度和时间的对应关系，图1给出了具有不同采样率的3个导航传感

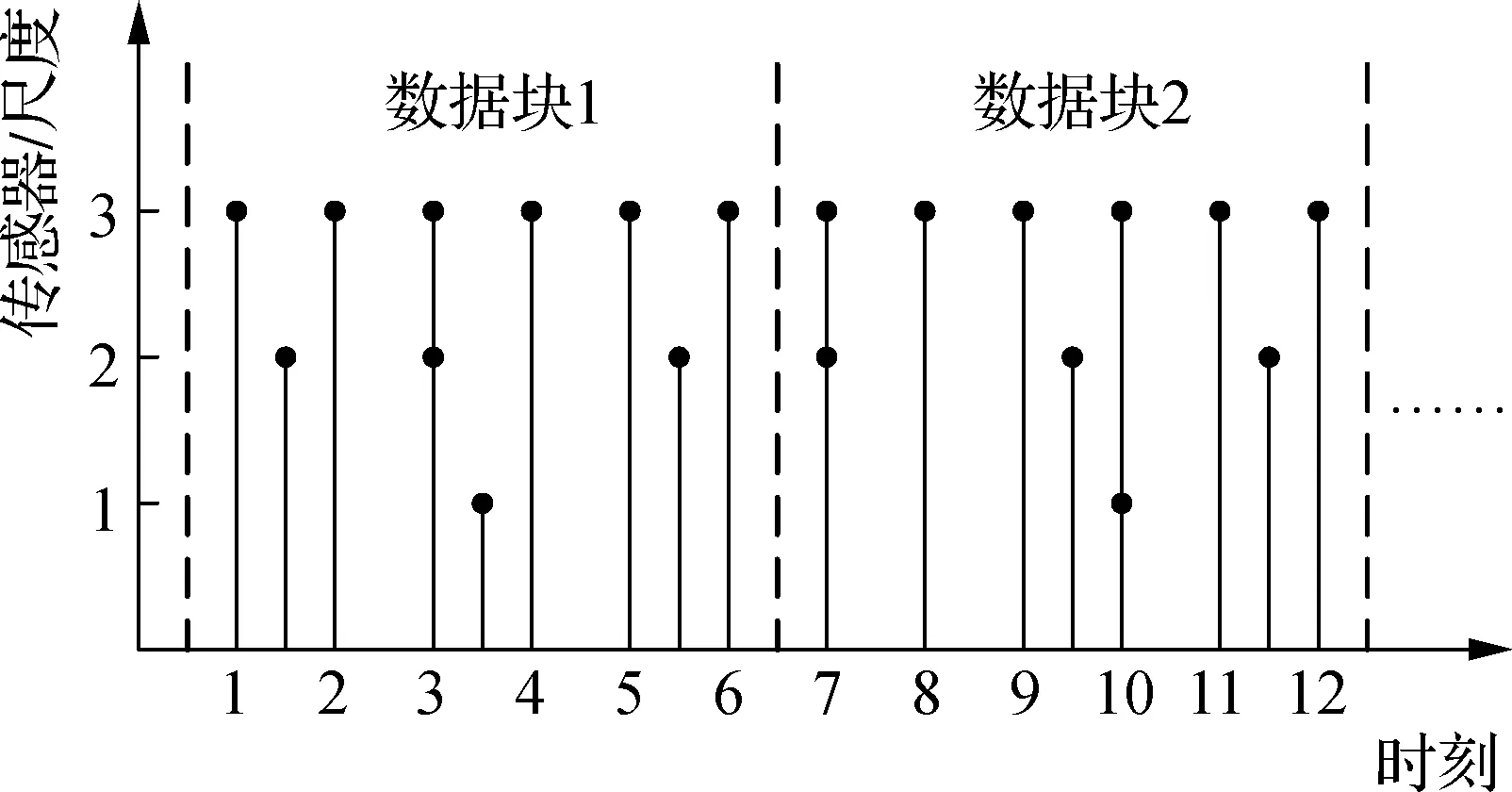
图1　多导航传感器异步采样示意图

器异步采样示意图.其中，横坐标表示时刻，纵坐标表示传感器(或尺度)，N=3，n1=3，n2=2.具有最高采样率的传感器N采样均匀，且其采样点与时刻一一对应，传感器i(i=1,2,…,N-1)的采样可以是非均匀的，即各传感器以多速率进行异步采样.

1.2　多尺度系统模型

x(N,kM+1)=Φ(N,kM)x(N,kM)+w(N,kM)

(4)

x(N,kM+2)=Φ(N,kM+1)Φ(N,kM)x(N,kM)+

Φ(N,kM+1)w(N,kM)+w(N,kM+1)

(5)

由数据归纳法，可得

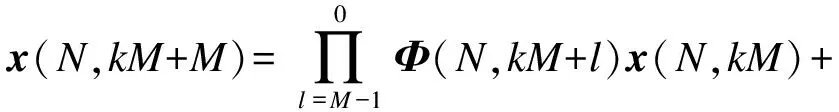
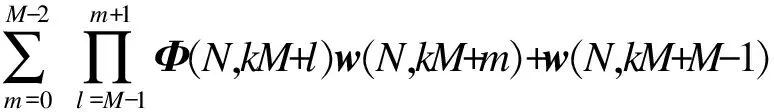
(6)

由式(4)～(6)，有

XN(k+1)=ΦN(k)XN(k)+WN(k)

(7)

(8)

(9)

(10)

(11)

根据1.1节所述w(N,k)均值为零、协方差为Q(N)，以及式(10)、(11)，可得

E{WN(k)}=0

(12)

(13)

(14)

现假设x(i,k)是最细尺度上的状态x(N,k)在尺度i上的平滑信息[15]，即

(15)

根据式(15)，有

x(i,(k-1)Mi+1)=

(16)

x(i,(k-1)Mi+j)=

(17)

根据式(3)、(16)和(17)，有

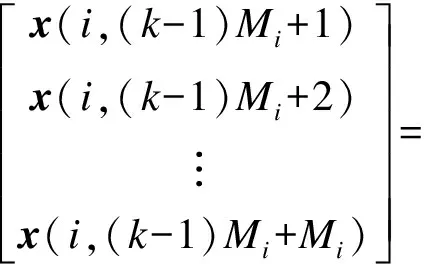
(18)

Zi(k)=Hi(k)XN(k)+Vi(k)

(19)

(20)

(21)

(22)

根据上节所述v(i,k) 均值为零、协方差为R(i)，且与w(N,l)不相关，以及式(10)、(22)，得

E{Vi(k)}=0

(23)

(24)

(25)

Ri(k)=diag{R(i,(k-1)Mi+1),

R(i,(k-1)Mi+2),…,R(i,kMi)}

(26)

综上，尺度i(i=1,2,…,N-1)上的系统模型为式(7)和(19).

2　信息融合估计算法

通常组合导航系统中具有最高采样率且采样均匀的传感器为捷联惯导系统(SINS)，即最细尺度N上的传感器为SINS.其余各导航子传感器可为多普勒测速仪(DVL)、里程计(OD)、全球定位系统(GPS)、地形辅助导航系统(TAN)等.

采用分布式的联邦滤波实现各导航传感器信息融合，即最细尺度N上的SINS分别与尺度i(i=1,2,…,N-1)上的各导航子传感器构成局部滤波器，则式(19)中第i个局部滤波器(即尺度i上)观测矩阵Zi(k)的第l个元素为

(27)

式中，1≤l≤Mi；D(i,*)为尺度i上导航传感器的量测信息；D(N,*)为相应的SINS解算信息.

(28)

(29)

相应的估计误差协方差矩阵为

(30)

综上，基于多尺度数据分块的组合导航信息融合算法流程图如图2所示.

图2　基于多尺度数据分块的组合导航信息融合算法流程图

3　仿真及分析

为验证本文所提信息融合算法的有效性，将所提方法用于SINS/DVL/TAN组合导航系统，利用Matlab进行相应的仿真试验.仿真中各传感器误差参数设置如表1所示.仿真时间为25 min，图3给出了仿真中载体的航行轨迹.载体从A点航行至B点，航行过程中包括左拐弯、右拐弯、加速、减速、匀速行驶等机动.载体在水平面航行，图4给出了仿真中载体航行速度和航向角.

表1　传感器误差参数

图3　载体航行轨迹

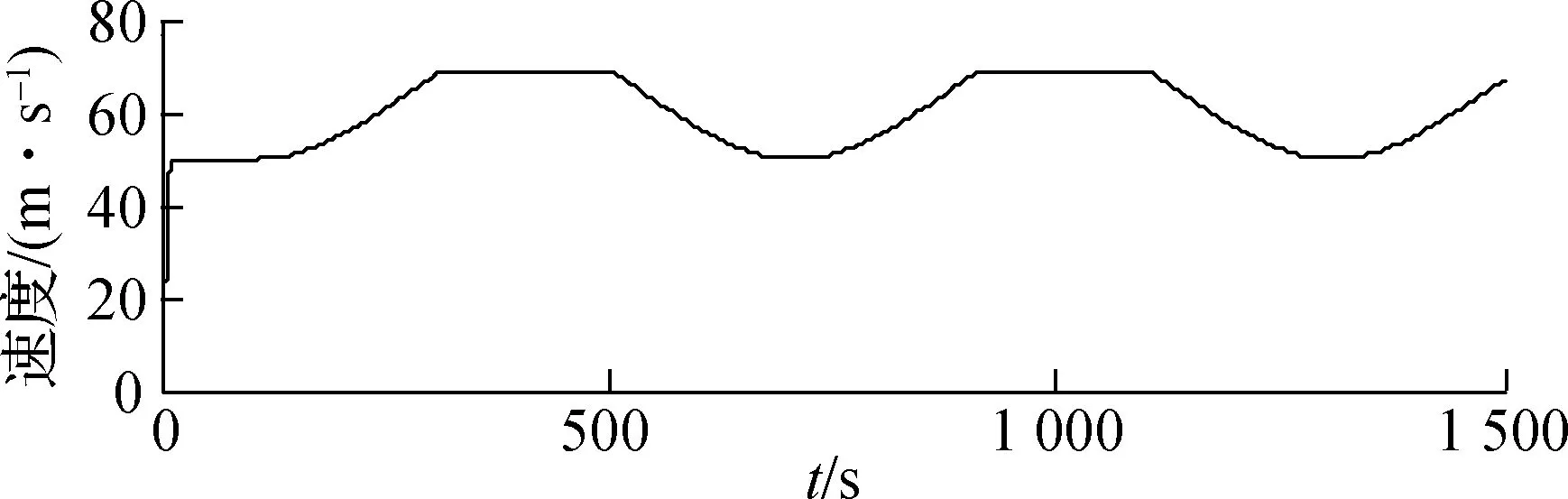
(a) 航行速度

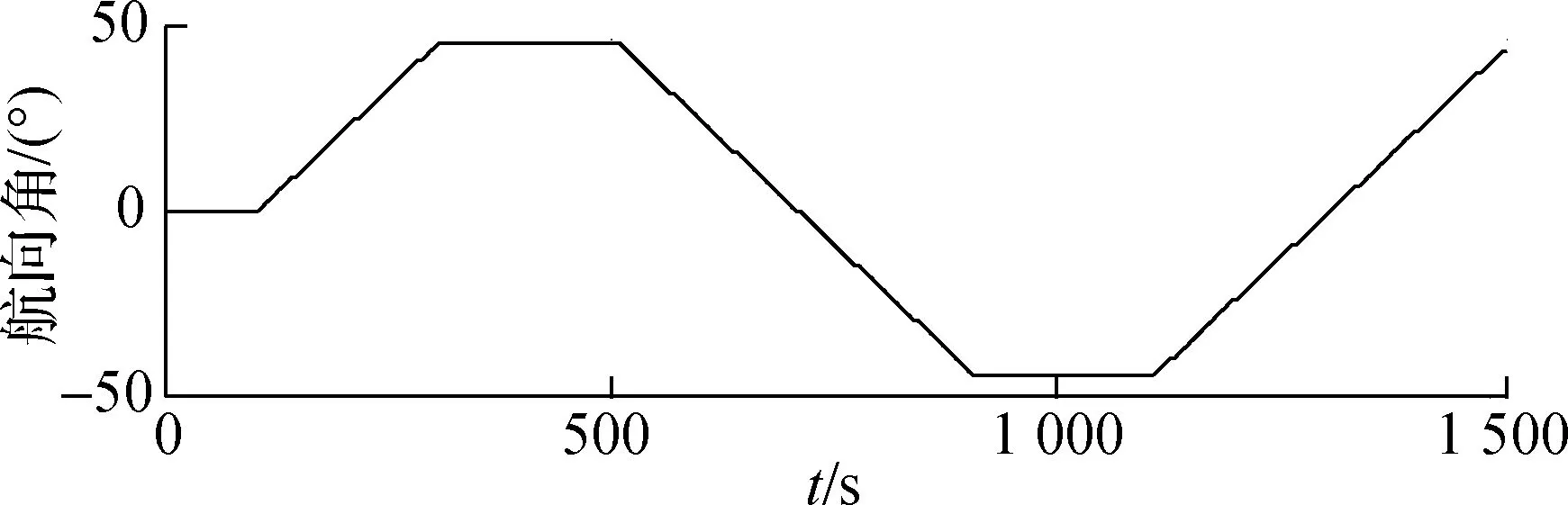
(b) 航向角

为模拟多传感器多采样率情况，设置SINS解算更新周期为0.02 s，DVL量测更新周期为0.5 s，TAN量测更新周期为1 s.各局部滤波器和主滤波器滤波更新周期均为1 s，主滤波器将局部滤波器输出信息进行最优融合.假设具有最高采样率的SINS采样均匀，为模拟传感器量测延迟情况，对DVL和TAN量测信息加入随机延时.

对于相同的SINS，DVL，TAN仿真数据，采用本文所提算法与非等间隔Kalman滤波法[14](简称算法1)进行信息融合比较.仿真中，本文所提算法将数据进行分块，且每个数据块均包含有3种导航传感器的量测信息，以数据块为单位进行滤波融合.算法1将与DVL，TAN量测对应的SINS解算结果存储，当延迟的DVL或TAN量测信息到达时，将其与存储的SINS解算结果相减，并将其作为观测量进行滤波，得到状态估计，并将此状态估计通过Kalman时间更新递推，得到当前时刻的状态估计值.仿真结果分别如图5和图6所示.表2给出了2种融合算法导航结果的数据统计值.

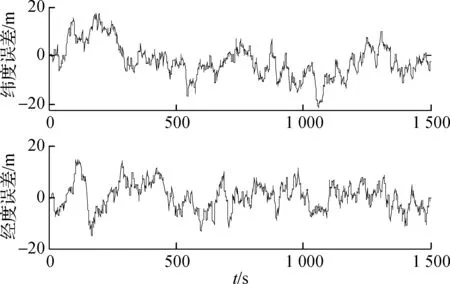
综合分析图5、图6和表2可得，本文算法与算法1相比，北向速度最大误差减小24.1%，纬度最大误差减小23.8%，东向速度最大误差和经度最大误差均略有减小.在多导航传感器异步采样的情形下，能有效提高滤波器的估计精度，从而有利于提高导航系统的定位精度.

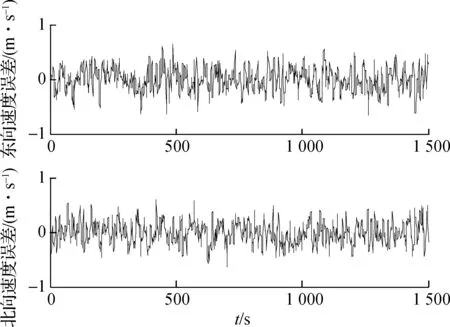
(a) 速度误差

(b) 位置误差

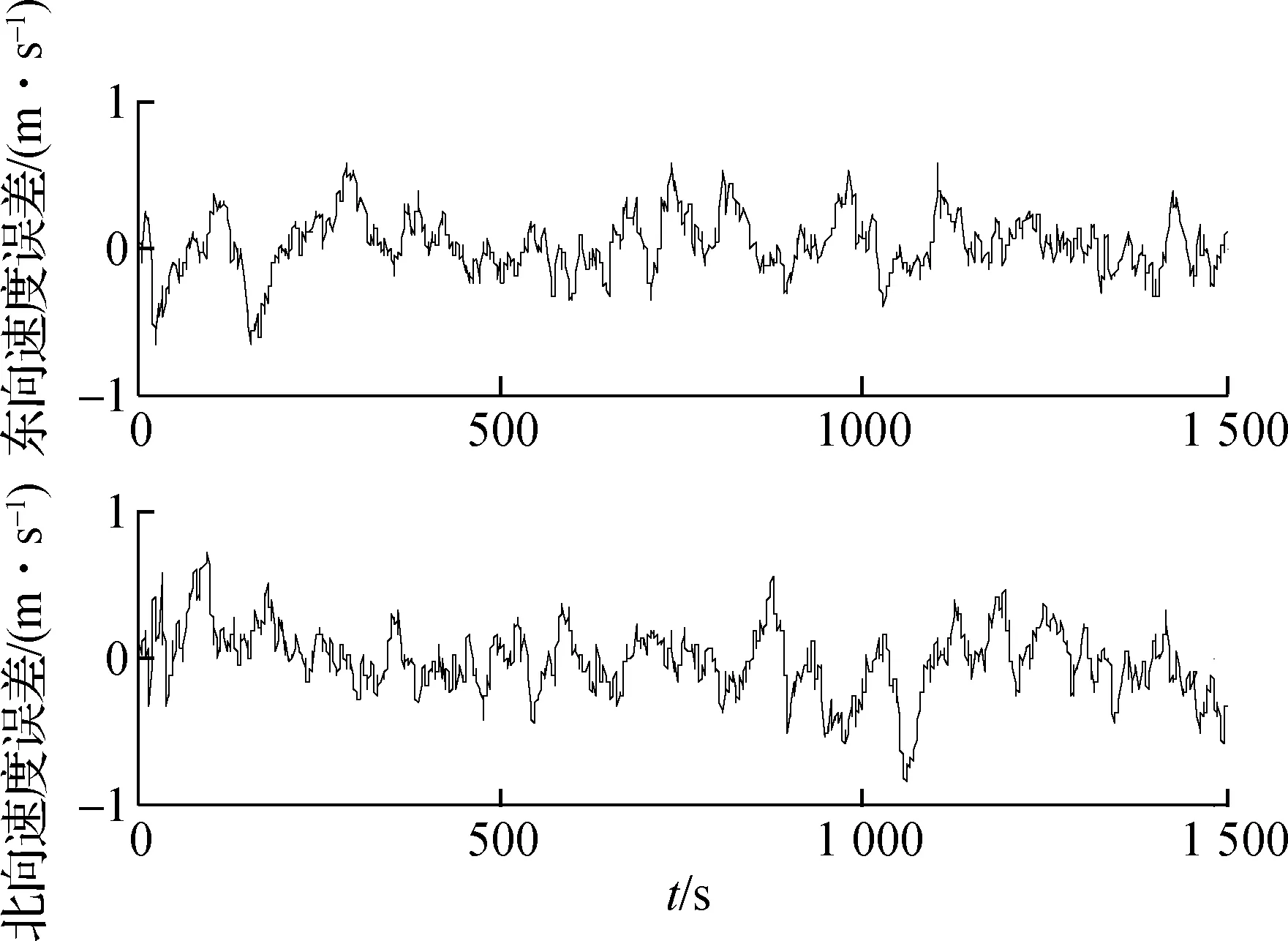
(a) 速度误差

(b) 航向角

算法误差项均方根最大绝对值本文算法东向速度误差/(m·s-1)0．18780．6487北向速度误差/(m·s-1)0．19970．6406纬度误差/m4．565514．21经度误差/m4．979916．21算法1东向速度误差/(m·s-1)0．19770．6552北向速度误差/(m·s-1)0．22570．8439纬度误差/m6．586121．27经度误差/m5．323716．53

4　结论

1) 以多传感器异步采样组合导航系统为对象，在导航传感器量测具有随机延迟的情况下，设计了一种基于多尺度数据分块的组合导航信息融合算法.将所提算法用于SINS/DVL/TAN组合导航系统进行仿真验证.通过处理包含所有传感器量测信息的数据块，有效解决了量测延迟问题.

2) 所提算法与非等间隔Kalman滤波算法相比，进一步减小了速度误差和位置误差，从而有利于提高系统导航精度.

但该算法也存在不足，通过状态和观测的分块建立多尺度系统模型的过程中，状态向量和观测向量的维数有所扩展，这将增加计算量和计算复杂度，因此如何进一步优化算法有待研究.

参考文献(References)

[1] Carlson N A. Federated filter for fault-tolerant integrated navigation systems[C]//IEEEPositionLocationandNavigationSymposium. New York, USA, 1988: 110-119. DOI:10.1109/plans.1988.195473.

[2] 张辉, 牛小骥, 郭文飞，等. 一种简易通用的敲击触发式惯性导航系统时间同步装置设计[J]. 传感技术学报, 2015, 28(1): 13-18.

Zhang Hui, Niu Xiaoji, Guo Wenfei,et al. A universal INS time synchronization solution based on punch triggering[J].ChineseJournalofSensorsandActuator, 2015,28(1): 13-18. (in Chinese)

[3] Gabrlik P, Jelinek A, Janata P. Precise multi-sensor georeferencing system for micro UAVs[C]//14thIFACConferenceonProgrammableDevicesandEmbeddedSystems. Brno, Czech Republic, 2016: 170-175.

[4] Ning X L, Gui M Z, Xu Y Z,et al. INS/VNS/CNS integrated navigation method for planetary rovers[J].AerospaceScienceandTechnology, 2016,48: 102-114. DOI:10.1016/j.ast.2015.11.002.

[5] Yang C S, Wang Q. Low cost integrated navigation system for unmanned vessel[J].PolishMaritimeResearch, 2017,24(3): 110-115. DOI:10.1515/pomr-2017-0112.

[6] Li Z K, Wang J, Li B H, et al. GPS/INS/odometer integrated system using fuzzy neural network for land vehicle navigation applications[J].JournalofNavigaiton, 2014,67(6): 967-983. DOI:10.1017/s0373463314000307.

[7] Ni Z F, Sunderrajan S, Rahimi A, et al. Distributed particle filter tracking with online multiple instance learning in a camera sensor network[C]//IEEEInternationalConferenceonImageProcessing. Hong Kong, China, 2010: 37-40.

[8] Nilsson J O, Handel P. Time synchronization and temporal ordering of asynchronous sensor measurements of a multi-sensor navigation system[C]//IEEEPosition,LocationandNavigationSymposium. Indian Wells, CA, USA, 2010: 897-902. DOI:10.1109/plans.2010.5507193.

[9] 赫飞, 丁姚, 张永伟. SINS/GPS/SST/高度表组合导航系统异步融合算法[J]. 海军航空工程学院学报, 2015, 30(1): 17-22.

He Fei, Ding Yao, Zhang Yongwei. Fusion-algorithm of asynchronous in the SINS/GPS/SST/altimeter integrated navigation system[J].JournalofNavalAeronauticalandAstronauticalUniversity, 2015,30(1): 17-22. (in Chinese)

[10] 刘磊, 林雪原, 周旻. 多传感器组合导航系统的多尺度异步信息融合算法[J]. 海军航空工程学院学报, 2012, 27(3): 276-280.

Liu Lei, Lin Xueyuan, Zhou Min. Multi-scale asynchronous information fusion algorithm of multi-sensor integrated navigation system[J].JournalofNavalAeronauticalandAstronauticalUniversity, 2012,27(3): 276-280. (in Chinese)

[11] Safari S, Shabani F, Simon D. Multirate multisensor data fusion for linear systems using Kalman filters and a neural network[J].AerospaceScienceandTechnology, 2014,39: 465-471. DOI:10.1016/j.ast.2014.06.005.

[12] Yang H, Li W, Luo C M. Integrated SINS/WSN positioning system for indoor mobile target using novel asynchronous data fusion method[J].JournalofSensors, 2017，2017: 7879198-1-7879198-12. DOI:10.1155/2017/7879198.

[13] Lin H L, Sun S L. Distributed fusion estimator for multi-sensor asynchronous sampling systems with missing measurements[J].IETSignalProcessing, 2016,10(7): 724-731. DOI:10.1049/iet-spr.2016.0017.

[14] 刘建业, 熊智, 段方. 考虑量测滞后的INS/SAR组合导航非等间隔滤波算法研究[J]. 宇航学报, 2004, 25(6): 626-631.

Liu Jianye, Xiong Zhi, Duan Fang. Processing the measurement delay INS/SAR integrated navigation in-coordinate interval filtering algorithm study[J].JournalofAstronautics, 2004,25(6): 626-631. (in Chinese)

[15] Yan L P, Liu B S, Zhou D H. The modeling and estimation of asynchronous multirate multisensor dynamic systems[J].AerospaceScienceandTechnology, 2006,10(1): 63-71. DOI:10.1016/j.ast.2005.09.001.