铅酸电池机理模型的简化求解

吕 超 ，葛腾飞 ，丛 巍 ，于洪海 ，赖庆智

（1.哈尔滨工业大学电气工程及自动化学院，哈尔滨150001；2.国网黑龙江省电力有限公司检修公司，哈尔滨150090）

铅酸电池广泛应用于汽车、通讯、电力、铁路等领域，是目前应用最为广泛的化学电源，其中阀控式密封铅酸 VRLA（valve-controlled lead acid）电池由于具有高温性能好、浮充寿命长、自放电性能好、价格相对低廉等优点而占领了较大份额的市场。电池的广泛应用对其使用和维护提出了更高的要求。更精确地仿真电池端电压行为和评估电池性能对于最大限度地发挥电池的作用必不可少，而这对电池模型提出了较高的要求。

目前铅酸电池的模型主要有等效电路模型、神经网络模型、机理模型等[1]。等效电路模型根据电化学阻抗谱应用电学元件近似表示电池内部的物理化学过程，具有结构简单、参数少等特点[2]，但是该模型精度较低且参数的物理意义不够明确，用于电池健康状态评估时参考价值不大；神经网络模型不用考虑电池内部细节，但是需要大量训练样本数据对网络进行训练，且误差受训练数据和训练方法的影响较大[3]；机理模型建立在传质理论和电化学反应上[4]，对电池端电压行为的仿真有很好的精确度，并且其模型参数具有明确的物理意义，能够更加明确地用于电池健康状态的评估。因而，本文对铅酸电池机理模型进行简化，并采用伽辽金法（Galerkin method）实现对模型的求解。最后针对不同工况仿真电池端电压行为及内部状态量，验证了模型简化和求解的正确性和精确度。

1 机理模型的简化

对于VRLA电池，充放电过程中其内部各个变量和电化学反应在高度和宽度上近乎均匀分布，因此只考虑极板厚度方向，其机理模型原理如图1所示，包括正负极集流体、正负极极板和隔膜，其中用下标p、s、n分别表示正极、隔膜和负极。为对模型做出化简，以兼顾模型的复杂度和精确度，做出如下假设：①忽略析气过程和其他副反应；②忽略固相电势在极板厚度方向上的分布；③忽略模型中各参数随温度和荷电状态的变化。

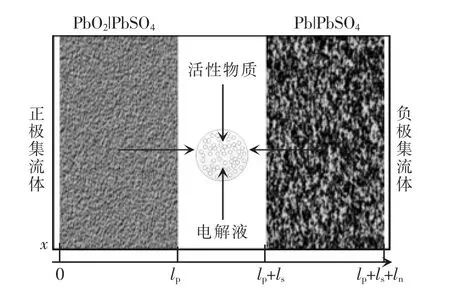
图1 铅酸电池机理模型原理Fig.1 Schematic of mechanism model of lead-acid battery

1.1 离子扩散与迁移

对于铅酸电池而言，正负离子均参与了充放电的反应，电解质为二元电解质（H+和HSO-4），其传输性能由所有离子的性质决定。离子在电解液中的传递通过扩散和迁移来完成，扩散过程遵循菲克扩散第二定律，而迁移过程主要与物质的淌度有关[6]。电解质的物质平衡方程描述为

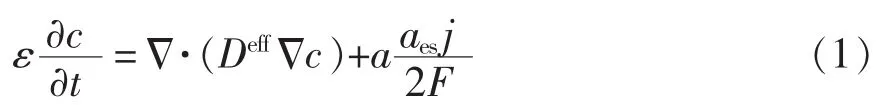
式中：ε为电解质体积分数；Deff为电解液有效扩散系数；正极中 a=3-2t+，负极中 a=1-2t+，其中 t+为 H+的迁移系数；aes为电极活性材料的比表面积；j为固相-液相界面处的反应电流密度；F为法粒第常数；c为电解液浓度；Δ为散度运算符。

以正极为例，边界条件为

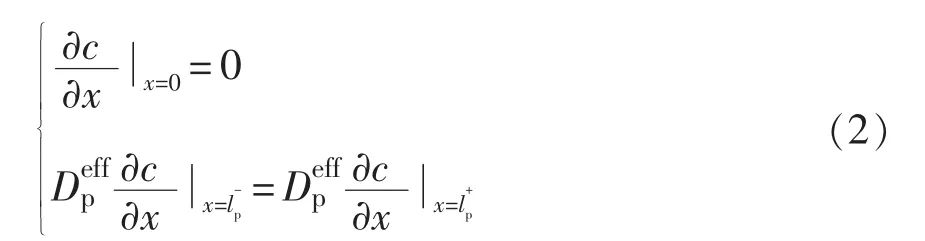
1.2 电荷平衡与欧姆定律

考虑固相材料的高导电性[7]，认为固相电势在正极区域和负极区域均匀分布。根据is=-σeffΔφs，φs为固相电势，则固相电流为0。

在正极、隔膜和负极的电解液中，液相电势由离子电流的欧姆定律与离子迁移电势构成[8]，即

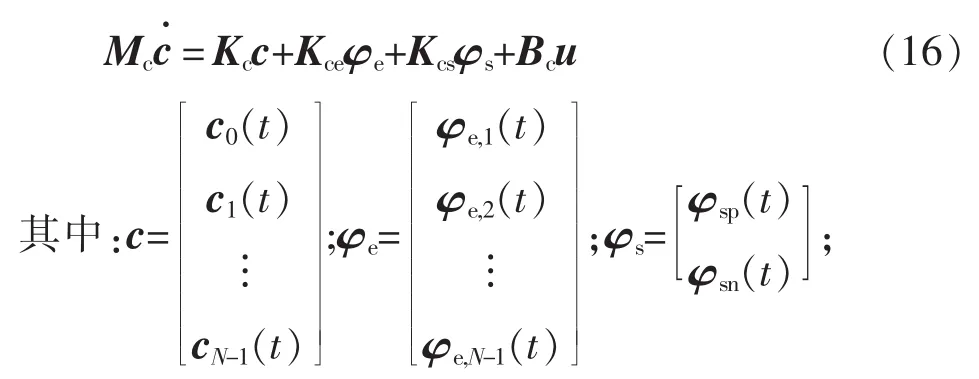
式中：φe为液相电势；ie为液相电流密度；κeff为有效液相电导率；为有效扩散电解质电导率，用于描述因离子扩散引起的电荷转移。

以正极为例，边界条件为

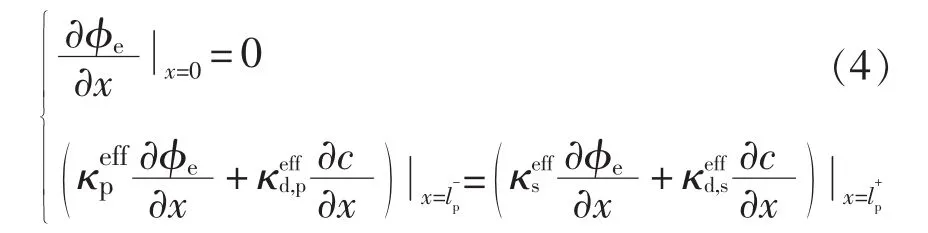
由固相液相交界面处的电荷守恒得到

式中，idl为单位体积的双电层电流密度，，Cdl为单位体积的双电层电容。

固相电流为0，则液相电流等于外电流密度。根据正负极的电荷守恒可得

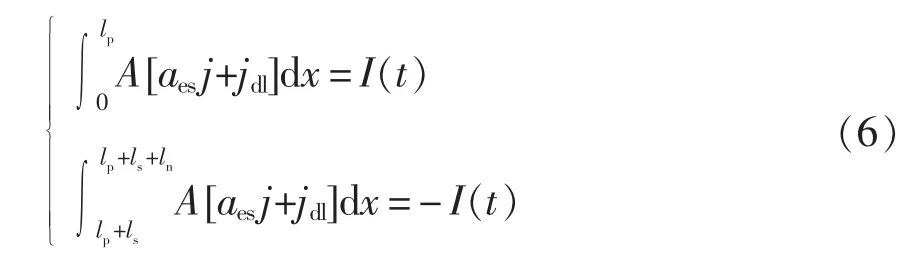
式中：lp、ls、ln分别为正极、 隔膜和负极的厚度；A 为极板有效面积。

1.3 电极动力学过程

电极动力学方程描述固相-液相界面处的反应离子流密度j与其界面过电势η的关系，反映界面处电化学反应的快慢程度，遵循Butler-Volmer动力学[9]，可描述为

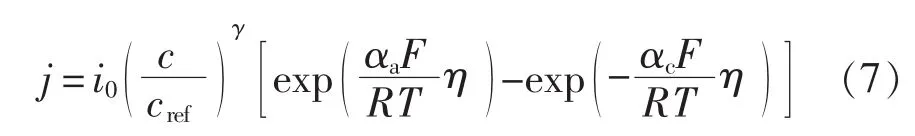
式中：i0为交换电流密度；cref为电解液参考浓度；γ为方程指数；αa和αc分别为阳极和阴极转移系数，αa+αc=n=2，n为反应中的电子数量；R为摩尔气体常数；T为电池温度。

在过电势η0=0附近对其进行一阶泰勒展开，即

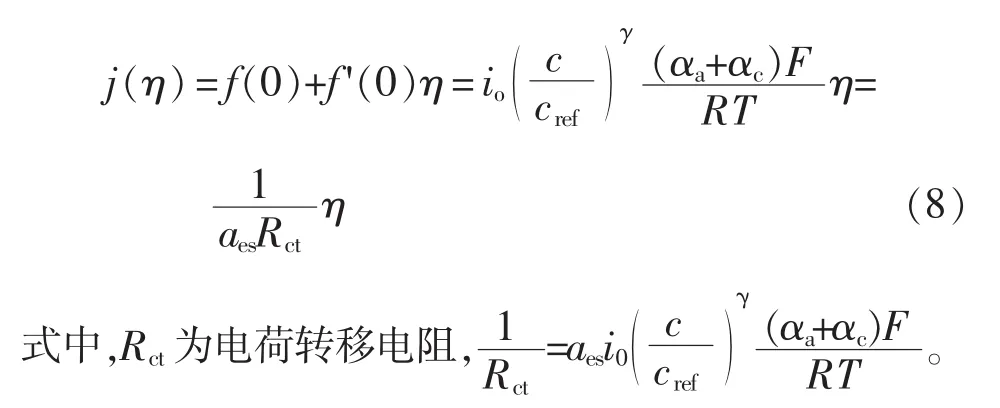
过电势η、固相电势φs、液相电势φe的关系为

式中：φsp、φsn为正、 负极固相电势；ΔUPbO2为与电解液浓度有关的电池开路电势，等于PbO2电极平衡电势与电极平衡电势之差[10]。其中，PbO2电极的平衡电势为

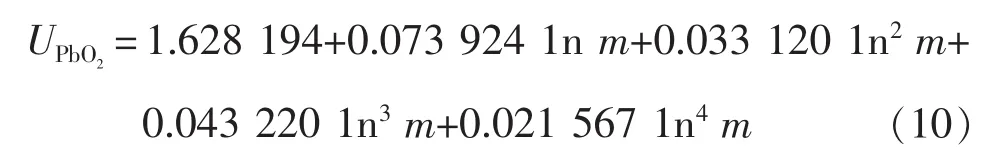
Pb电极的平衡电势为

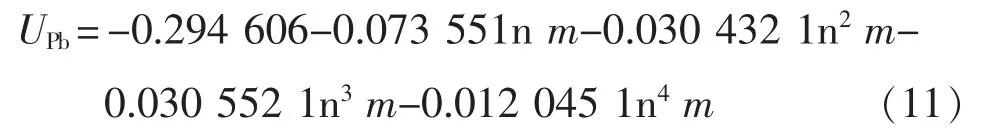
式中，m为电解液的摩尔质量，m=1.003 22×103c+3.55×104c2+2.17×106c3+2.06×108c4。

开路电势与电解液浓度c之间的关系如图2所示。由图2可见，在1＜c＜8 mo1/L的条件下，开路电势ΔUPbO2与c具有较好的线性相关度，即

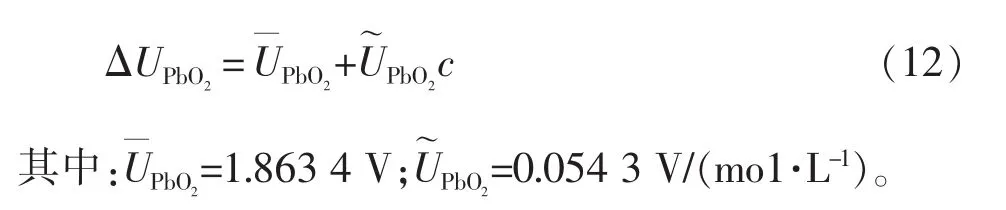
正负极集流体连接到电极的末端区域（x=0和x=L），集流体处电压等于该位置处的固相电势。电池的输出电压为正、负极集流体之间的电势差正负极固相电势之差，即

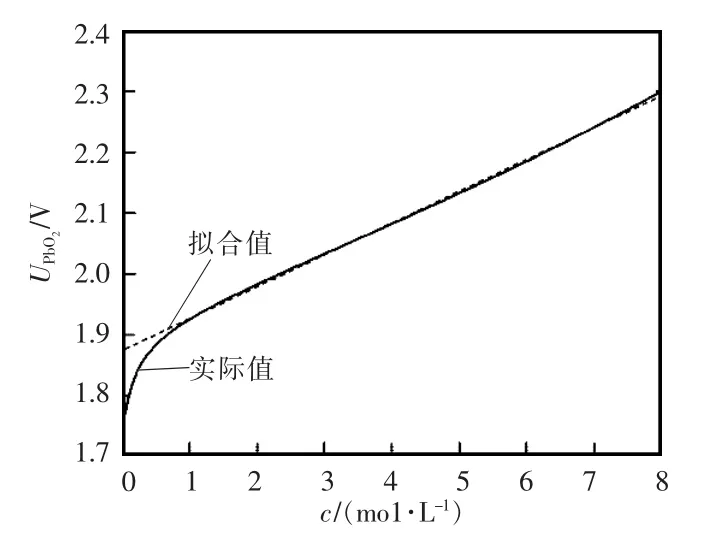
图2 开路电势与电解液浓度c之间的关系Fig.2 Relationship between open circuit potential and electrolyte concentration c

2 简化模型的求解

从系统的角度来看，电池本质上是一个单输入单输出系统，即输入电流、输出电压。为了求解模型必须对偏微分方程组进行离散化得到常微分方程组。由于伽辽金法精度较高，而且巧妙地运用了偏微分方程的弱形式，计算量不大[11,12]。本文采用此法对模型进行求解。

考虑到集流体处零通量的边界条件（x=0和x=L，L=lp+ls+ln），试函数选取，则电解液浓度和液相电势分别可表示为

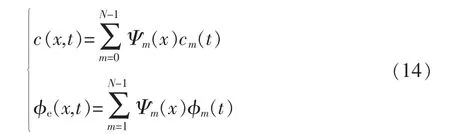
式中：cm（t）和 φm（t）分别为电解液浓度和液相电势的伽辽金系数；N为伽辽金阶数。

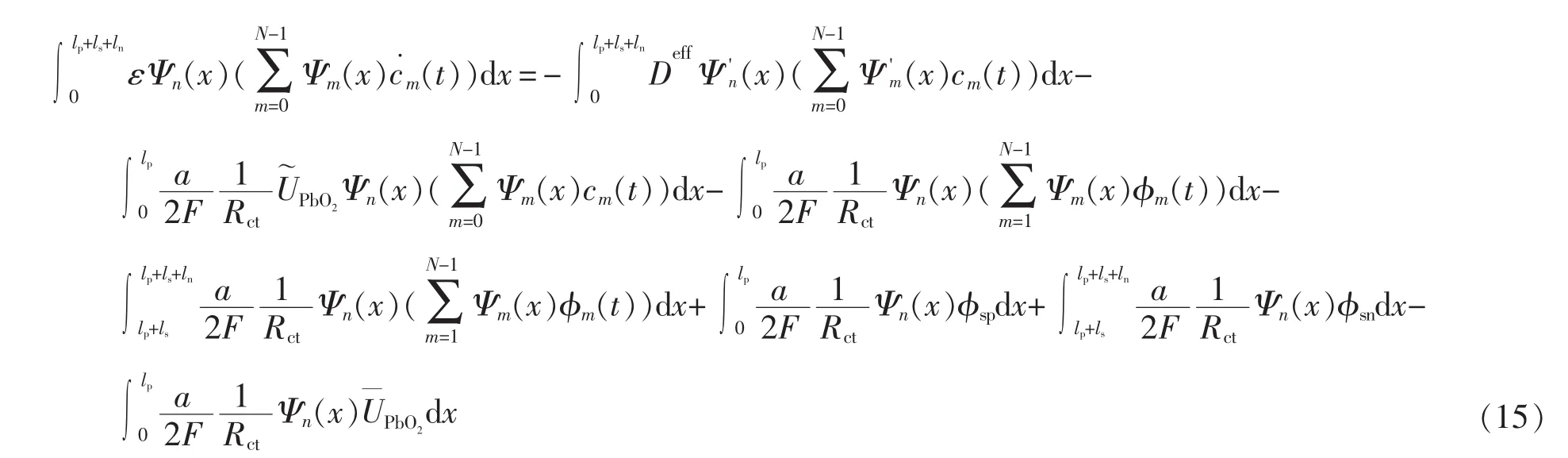
将其转换为矩阵形式，即

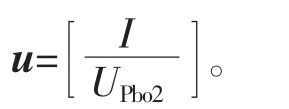
对式（3）和式（5）的域内剩余与权函数做内积，可得

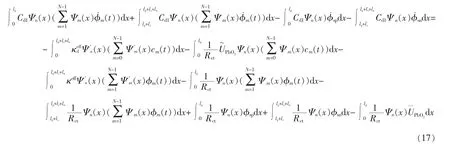
将其转换为矩阵形式，即

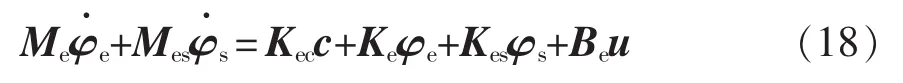
对式（6）的域内剩余与权函数做内积，可得

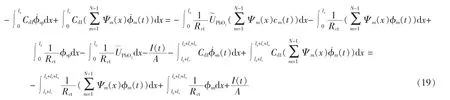
将其转换为矩阵形式，即

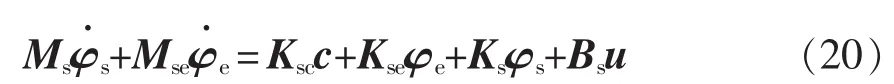
将式（14）、式（16）、式（18）统一成状态空间方程的形式，即

3 简化模型的参数辨识和仿真验证

选取哈尔滨光宇电源有限公司的GFMG-100阀控式密封铅酸蓄电池对模型进行验证，其额定电压2 V，C10时率下放电容量100 Ah，采用Neware电池测试系统对其进行充放电实验。模型求解采用5阶伽辽金近似解，未知参数采用遗传算法进行辨识得到[13,14]，辨识工况为DST工况，目标函数为模型仿真端电压与实测值的均方根误差，即

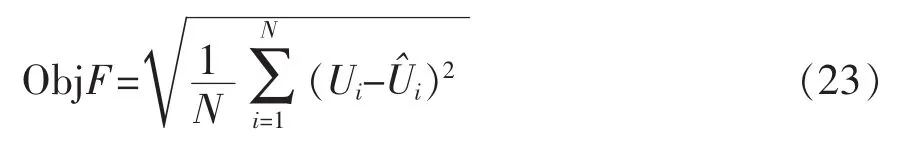
式中：Ui为代入一组参数后模型输出端电压；为电池实测端电压数据；N为数据采样点个数。

仿真程序采用MATLAB语言编写，基于英国谢菲尔德大学开发的遗传算法工具箱实现，算法参数设置如表1所示，待辨识参数采用实值编码，最终确定的模型参数如表2所示，其中前半部分为已知参数，后半部分为待辨识参数。

表1 遗传算法相关参数设定Tab.1 Setting of related parameters in genetic algorithm

表2 铅酸电池机理模型参数Tab.2 Parameters in the mechanism model of lead-acid battery

根据辨识得到的参数，结合机理模型及其伽辽金近似解，对模型和参数进行实验验证。

在环境温度20℃条件下，对电池进行5 A恒流放电，放电时间15 min，仿真结果如图3所示。由图（a）可以看出，仿真电压和实测电压几乎一致。不同时刻的电解液浓度分布如图3（b）所示，在放电过程中，正负极都会消耗酸，而隔膜处的酸液不会消耗，而是向正负极扩散，式（1）中正极的系数a和活性材料比表面积as较大，故而正极中酸的消耗速度要比负极快，这与文献[10]中数据保持一致。而电池内部的其他状态量如极化过电势、反应离子流密度、固液相电势等分布也分别可求。

对电池进行某一特定的动态工况实验，不同的充放电倍率和时间交替，其验证工况和相应的端电压实测及仿真数据如图4所示，可以看出，端电压的平均误差为5.9 mV，相较于铅酸电池2 V的电压平台相对误差仅有0.295%；在电流较大时，仿真误差相对较大，最大误差为12.6 mV。分析原因是由于对电极动力学方程在过电势为零附近进行一阶泰勒展开所导致，在电流较大时线性化误差较大，从而端电压仿真误差较大。验证结果表明，提出的模型能够比较精确地仿真铅酸电池的端电压行为。

所设计的验证工况时间为104 min，采样时间为1 s，即共有6 240个点，仿真程序采用MATLAB语言编写，仿真环境为 Inter（R） Core（TM） i3 CPU 530@2.93GHz and 2G RAM，仿真时间为116.895 ms，这对于铅酸电池机理模型用于在线仿真提供了一定的可能性。

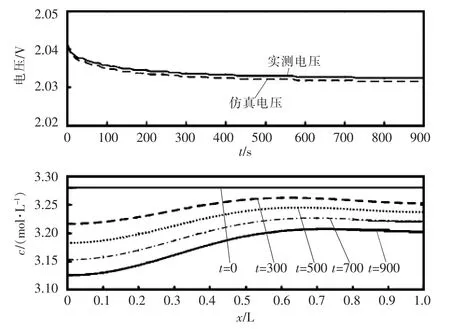
图3 恒流放电工况下模型的仿真结果Fig.3 Simulation results of the model under the operation condition of constant current discharge

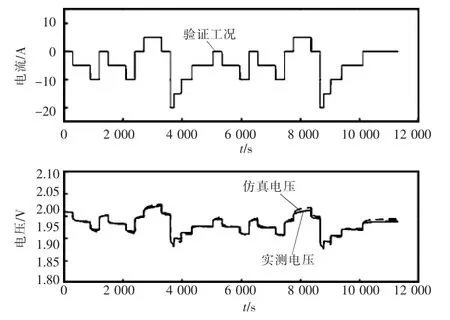
图4 动态验证工况下电池模型的仿真结果Fig.4 Simulation results of the model under operation condition of dynamic verification

4 结语

本文通过对铅酸电池机理模型的电极动力学过程和开路电势进行近似，忽略固相电势在正负极区域的分布，提出了一种简化的铅酸电池机理模型，同时采用伽辽金法并选取余弦函数作为试函数进行求解。经实验验证，模型能够较好地模拟电池的端电压行为，动态工况下其平均相对误差仅为0.295%。模型具有较快的求解速度，这为机理模型应用于电池管理系统的在线仿真提供了一定的可能性，可以考虑将其应用于电动车的嵌入式系统中。相较于等效电路模型，机理模型内部参数具有明确的物理意义，后续的工作可以针对铅酸电池不同老化状态下的模型参数，结合老化机理选取表征电池健康状态的特征量，然后基于粒子滤波、支持向量机等算法对电池的健康退化趋势进行判断和预测。对于变电站和通讯基站的备用铅酸电池组而言，相较于传统的核对性充放电和内阻测量，该方法具有对电池损害小和检测时间短的特点，不失为铅酸电池健康状态评估的一种全新解决思路。

参考文献：

[1]张彦琴,郭凯,刘汉雨.铅酸电池模型及参数辨识研究[J].蓄电池,2013,50 （3）:140-144.Zhang Yanqin,Guo Kai,Liu Hanyu.Research on equivalent model and its parameters identification of lead-acid batteries[J].Chineses Labat Man,2013,50 （3）:140-144（in Chinese）.

[2]Chen Min,Rincon-Mora G A.Accurate electrical battery model capable of predicting runtime and IV performance[J].Energy Conversion,IEEE Transactions on,2006,21（2）:504-511.

[3]Yuan Yuan,Sun Chengchen,Li Mengting,et al.Determination of optimal supercapacitor-lead-acid battery energy storage capacity for smoothing wind power using empirical mode decomposition and neural network[J].Elec-tric Power Systems Research,2015,127:323-331.

[4]Newman J,Tiedemann W.Porous-electrode theory with battery applications[J].AIChE Journal,1975,21（1）:25-41.

[5]Hu Y,Yurkovich S,Guezennec Y,et al.Electro-thermal battery model identification for automotive applications[J].Journal of Power Sources,2011,196（1）:449-457.

[6]Esfahanian V,Ansari A B,Torabi F.Simulation of leadacid battery using model order reduction[J].Journal of Power Sources,2015,279:294-305.

[7]Gu W B,Wang C Y,Liaw B Y.Numerical modeling of coupled electrochemical and transport processes in lead-acid batteries[J].Journal of the Electrochemical Society,1997,144（6）:2053-2061.

[8]Rahn C D,Wang Chaoyang.Battery systems engineering[M].New Jersey:John Wiley&Sons,2013.

[9]Gu W B,Wang G Q,Wang C Y.Modeling the overcharge process of VRLA batteries[J].Journal of Power Sources,2002,108（1）:174-184.

[10]Cugnet M,Laruelle S,Grugeon S,et al.A mathematical model for the simulation of new and aged automotive lead-acid batteries[J].Journal of the Electrochemical Society,2009,156（12）:A974-A985.

[11]老大中.变分法基础[M].2版.北京:国防工业出版社,2007.

[12]Shi Ying,Prasad G,Shen Zheng,et al.Discretization methods for battery systems modeling[C]//American Control Conference （ACC）,2011.San Francisco,CA,USA,2011:356-361.

[13]Zhang Liqiang,Wang Lixin,Hinds G,et al.Multi-objective optimization of lithium-ion battery model using genetic algorithm approach[J].Journal of Power Sources,2014,270（3）:367-378.

[14]Blaifi S,Moulahoum S,Colak I,et al.An enhanced dynamic model of battery using genetic algorithm suitable for photovoltaic applications[J].Applied Energy,2016,169:888-898.