基于分数阶重复PI控制的并网逆变器设计

邹 叶，陈 嵘，沈正斌，李 鹏,郭有贵

（湘潭大学控制工程研究所，湘潭 411105）

LCL型并网逆变器要求输出并网电流与电网频率、相位一致，抑制电流的谐振尖峰，常常通过改善LCL滤波器和电流控制策略来解决问题[1-2]。文献[3]将LCL的电容支路分成两个部分，只在其中一半电容上串联阻尼电阻，通过选择合适的阻尼电阻，解决了LCL型逆变器的电流谐振问题，也降低了阻尼电阻的功率损耗；文献[4]在不增加额外传感器的前提下，提出了基于带通滤波器的有源阻尼控制策略，很好地控制了谐振频率多变的系统；文献[5]提出反馈分裂电容的中间电流，使受控系统从三阶转换为一阶，减小了稳态误差和电流谐波失真；文献[6]分析了电容串联虚拟电阻和并联虚拟电阻的两种有源阻尼方法的阻尼原理，证明了虚拟电阻能在避免功率损耗产生的情况下，有效抑制谐波。加入无源阻尼实现上简单，但存在有功功率损耗，降低了系统的效率，所以常选用有源阻尼的方法。

常用的电流控制策略有PI控制、比例谐振控制、无差拍控制、重复控制以及复合控制等方式[7-10]。PI控制算法简单，动态响应快，也易于实现；无差拍控制是一种数字控制方法，能预测下一个开关周期的控制信号；比例谐振控制器和重复控制都基于内模原理，能很好地消除周期性谐波，在基波频率处可以消除系统的稳态误差；复合控制结合多种控制策略的优点，成为当前的研究热点，但由于加入LCL有源阻尼，使系统复杂化，可调节参数增多。

本文针对并网逆变器中周期性扰动产生波形畸变及LCL滤波器的谐波问题，提出了一种基于分数阶相位超前重复控制与PI调节复合控制方案。该方案根据LCL滤波器中电容并联的电阻等效，通过传递函数推导出了前向通道上的等效环节，将该环节替代重复控制补偿器中的低通滤波器，简化了重复控制器的参数推算，保证了零相移的精确度，同时提高了系统的动态性能和稳态性能。

1 系统数学模型

图1为带LCL滤波器的并网型逆变器。图中，LCL滤波器包括3部分：变流器侧电感Li、并网侧电感Lg和滤波电容Cf。由于线路以及电感的电阻很小，分析中忽略其阻值。其中，Udc为直流侧电压，Idc为直流侧电流；交流侧三相分别为a、b、c相，且Ug和 Ig、Uc和 Ic、Ui和 Ii表示电网侧相电压滤波电容和相电流、滤波电容器相电压、相电流、变换器输出相电压和相电流。

在基波频率下，该拓扑结构电网可视为理想电压源。图1中LCL型滤波器的逆变器侧电感支路、网侧电感支路、电容支路的电路方程分别为

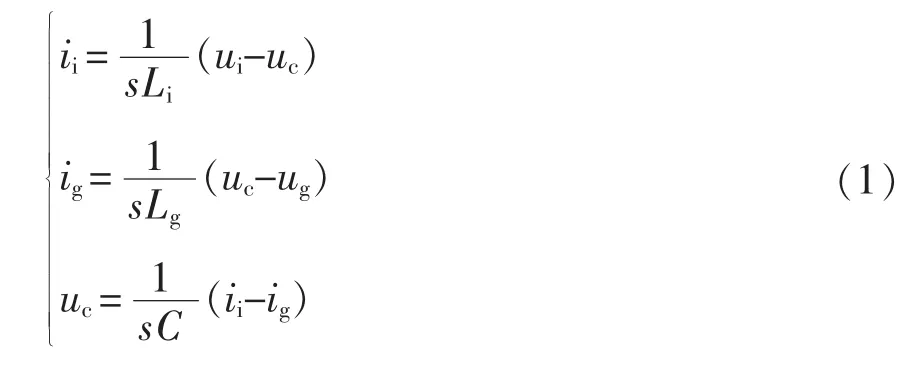
图1 LCL型并网逆变器主电路拓扑Fig.1 Main circuit topology of LCL-type grid-connected inverter

在谐波频率下，电网可视为短路，即Ug=0。以变流侧电压Ui为输入，并网侧电流Ig为输出，消元可得传递函数为

2 LCL滤波器中虚拟电阻的设计

文献[6]通过对电容并联阻尼电阻的传递函数结构框图进行等效变换，提出了一种虚拟电阻并联电容的有源阻尼方法。本文通过假设虚拟电阻，保持传递函数不变，来推算有源阻尼表达式。

图2（a）为LCL滤波器电容并联电阻的结构框图，其传递函数为

图2（b）为将图2（a）中虚拟化，假设有源阻尼为 A（s），则

图2 电容并联虚拟电阻等效变换原理Fig.2 Equivalent transformation principle of capacitance parallel virtual resistor

通过式（2）和式（3）可得

电容按照吸收5%的无功功率，电感根据逆变器直流侧电压和最大纹波电流而定，系统最终采用的 LCL 滤波器参数为：Li=1 mH，Lg=4.5 mH，Cf=5 μF，R=100 Ω，对应的谐振频率为 15.6 kHz。

电容并联阻尼与无阻尼两种情况下的传递函数伯德图如图3所示。由图可见，无阻尼时，即使选取了合适的电容电感参数，依然存在谐振峰；而加上阻尼电阻后达到了很好的抑制效果。

电容并联电阻的纹波衰减函数为

图3 电容并联阻尼和无阻尼传递函数伯德图Fig.3 Bode diagrams of capacitance parallel damping and undamped transfer function

图4 电容并联电阻的纹波衰减函数伯德图Fig.4 Bode diagram of the ripple attenuation function of capacitance parallel resistance

只要R取较小的值，电容并联电阻就很容易达到高频纹波衰减，纹波衰减函数伯德图如图4所示。

该方法既避免了无源阻尼带来的功率损耗，保持了系统的稳定性，也没有引入更多的传感器。

3 分数阶重复PI控制器设计

3.1 传统重复控制

重复控制的基本控制策略，即内模原理，通过周期性方式能很好地消除周期性的谐波干扰。传统重复控制传递函数为

重复环节通过指数函数展开为

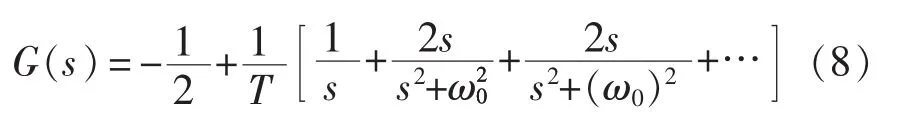
重复控制内膜离散模式为

式中：N为每个周期采样数，即系统的采样频率fs与基波频率f之比；Q（z）为保证系统收敛而加入的小于1的常数或者零相位低通滤波器。为提高整个系统的性能，需要针对被控对象设置重复控制器的补偿器，从而增加系统高频衰减能力。传统重复控制框图如图5所示。

图5 传统重复控制框图Fig.5 Block diagram of traditional repetitive control

图中，C（z）为补偿器，由控制增益 kr、超前环节zk（k＞0）、零相移陷波器 S1（z）、二阶低通滤波器 S2（z）4个部分组成。其中kr控制补偿量的强度，大小与收敛速度成正比，与系统的稳定裕度成反比；zk补偿由低通滤波器和被控对象引入的相位滞后，保持中低频段零相移；S1（z）用来补偿被控对象的谐振尖峰，将中低频段的增益校正为1；S2（z）能增强高频衰减特性，提高系统稳定性和高频抗干扰能力。C（z）的数学结构为

对于传统重复控制方案，当输入指令突然增加时，经过重复控制器的滞后环节后会影响跟踪速度，所以参考信号一般要通过前馈输入系统中。在实际应用中，一般采用图6所示的嵌入式重复控制结构。

图6 嵌入式重复控制框图Fig.6 Block diagram of embedded repetitive control

3.2 分数阶相位超前设计

重复控制补偿器中的超前环节为zk，k为正整数。令 G1（z）＝krS1（z）S2（z）P（z），zk对 G1（z）的相位补偿如图7所示。由图可知，当k＝2时，随着频率增大，超前环节无法补偿 G1（z）；k＝3 时，超前环节远远超过了G1（z）所需要的补偿。对于整数阶相位超前不能达到零相移的问题，本文提出了一种分数阶相位超前的方法，以提高相位校正的精确度。

令理想分数阶相位超前 H（z）＝zD，D≥0 且可为小数。基于有限冲击响应滤波器[11]的原理，根据GOetken和拉格朗日插值方法[12]，可以得到

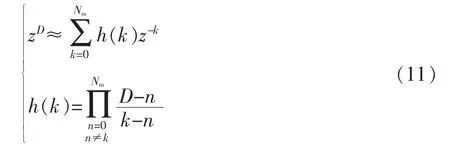
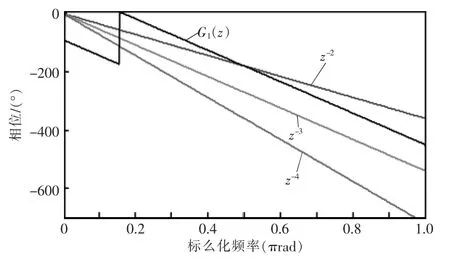
图7 整数阶超前环节相位补偿Fig.7 Compensation for integer-order phase lead

图8 分数阶超前环节相位补偿Fig.8 Compensation for fractional-order phase lead

由图7可知，D可取2～3间的小数，在此，取Nm=6，zD用zk表示，如表1所示。

zD对G1（z）的相位补偿如图8所示。由图可见，当D取2.4时，能很好地补偿重复控制和负载带来的相位滞后，提高了系统的稳态性能。

表1 分数阶转化成整数阶Tab.1 Conversion fraction-order into integer-order

3.3 分数阶重复控制与PI控制的复合设计

由上述分析可知，带补偿器的重复控制能实现输出对所给指令信号的无静差跟踪，稳态时输出波形稳定谐波很小，并网逆变器具有很好的稳态特性。但是，给定指令信号改变或者突加扰动时，系统并不能及时抑制。因为重复控制的瞬态响应速度慢，一般只用来调节周期扰动。而PI控制器正好能在扰动出现时及时调节，跟踪误差的响应速度快，能使系统具有很好的动态性能。

本文所设计的并网逆变系统采取并网电流单环控制，选用结合了重复控制的稳态特性和PI控制动态特性的控制策略，结构框图如图9所示。

图9 电流环复合控制结构框图Fig.9 Block diagram of compound control of current loop

图中，A（z）为LCL滤波器电容上并联的虚拟电阻，替代重复控制补偿器中的低通滤波器，则有

陷波器 S1（z）选取为梳状滤波器，即

式中，a为常数。陷波器在特定频率处的幅值迅速衰减。令 S1（θ）=0，相频特性一直为 0，不会引起相位滞后。该系统中a取2，r为6。

重复控制器的内膜中，周期延迟环节z-N与参考信号频率和开关频率关系为

4 仿真与实验

4.1 仿真验证

仿真参数为：并网电压Uabc=380 V、频率f=50 Hz；直流输入电压Udc=800 V；开关频率fs=10 kHz，延迟环节指数N=200。根据第2节所取的LCL滤波器参数，分别对无阻尼和有阻尼的情况进行仿真，仿真结果如图10所示。图（a）为无阻尼情况下的一相并网电流波形，由于LCL滤波器谐振尖峰的原因，电流处于发散状态；图（b）和图（c）分别为加入50 Ω和100 Ω的阻尼电阻，图（b）中存在明显的谐波，经过对比可知，选取合适的阻尼电阻能更好地抑制谐振尖峰。

该系统分别用PI控制、重复控制和复合控制3种控制方案进行控制，仿真波形如图11所示，在第5个周期结束时将并网电流的参考电流由50 A换成 90 A，通过图（b）和图（c）对比，在只有重复控制的情况下，改变参考电压的第二个周期开始才能准确校正，而复合控制在第一个周期就能达到参考电流值；对比图（a）和图（c），PI控制能快速校正电流，但是波形并不稳定，谐波偏大。由此表明，PI控制和重复控制结合的复合控制，能同时使系统具有很好的稳态性能和动态性能。

图10 虚拟阻尼方案仿真波形Fig.10 Comparison of waveform among virtual damping schemes

4.2 实验验证

实验平台为1.5 kW储能变流器，开关频率为10 kHz，主电路功率器件选用PM300RL1A060，LCL滤波器参数为：逆变器侧电感Li=1 mH，Lg=4.5 mH，Cf=5 μF。选用DSP2812控制芯片，处理并网侧电流信号。LCL型并网逆变器分别在PI控制和本文所提的复合控制下，稳定状态时的三相并网电流波形如图12所示，图（a）中存在明显谐波，采用复合控制的图（b）波形稳定。并网时a相电流电压的波形如图13（a），从并网状态转至离网时的波形如图13（b）。根据实验波形可见，该系统动态响应快，稳态性能很好，证明了本文提出方案的可行性。

图11 三相并网电流仿真波形Fig.11 Simulation waveform of three-phase gridconnected current

图12 三相并网电流实验波形Fig.12 Experimental waveforms of three-phase gridconnected current

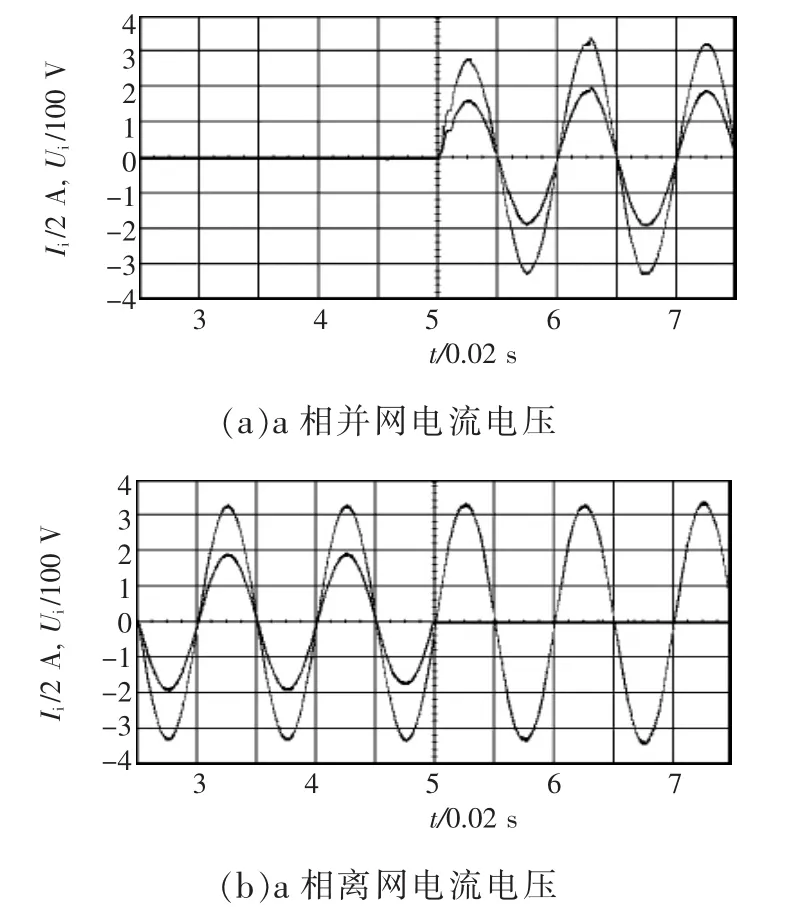
图13 a相电流、电压波形Fig.13 Waveforms of current and voltage in phase-a

5 结论

（1）采用了电容并联虚拟电阻，通过计算将电阻在前向通道中等效，与重复控制的补偿器结合，简化了重复控制器。

（2）由于PI控制稳态性能差，鲁棒性低，而重复控制对扰动响应慢，难以抑制暂态扰动。基于两种控制策略互补的特点，提出了结合PI控制和重复控制的复合控制方案。

（3）引用了分数阶算法，实现重复控制相位补偿中的分数阶相位超前。

分析、仿真和实验结果表明，系统成功地抑制了LCL滤波器中非线性元件带来的谐振尖峰，相比无源阻尼方法避免了额外的功率损耗产生，也没有增加传感器的数量；分数阶的应用，提供了更加精确的相位补偿方法，实现系统零相移；复合控制成功结合了PI控制和重复控制的优点，使系统同时具有很好的动态性能和稳态性能。

参考文献：

[1]王斯然,吕征宇.LCL型并网逆变器中重复控制方法研究[J].中国电机工程学报,2010,30（27）:69-75.Wang Siran,Lü Zhengyu.Research on repetitive control method applied to grid-connected inverter with LCL filter[J].Proceedings of the CSEE,2010,30（27）:69-75（in Chinese）.

[2]Tang Yi,Loh P C,Wang Peng,et al.Generalized design of high performance shunt active power filter with output LCL filter.IEEE Transactions on Industrial Electronics,2011,59（3）:1443-1452.

[3]王海松,王晗,张建文,等.LCL型并网逆变器的分裂电容无源阻尼控制[J].电网技术,2014,38（4）:895-902.Wang Haisong,Wang Han,Zhang Jianwen,et al.Split-capacitor passive damping control for LCL grid-connected inverter[J].Power System Technology,2014,38（4）:895-902（in Chinese）.

[4]尹靖元,金新民,吴学智,等.基于带通滤波器的LCL型滤波器有源阻尼控制[J].电网技术,2013,37（8）:2376-2382.Yin Jingyuan,Jin Xinmin,Wu Xuezhi,et al.Active damping control strategy for LCL filter based on band pass filter[J].Power System Technology,2013,37（8）:2376-2382（in Chinese）.

[5]沈国桥,徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制[J].中国电机工程学报,2008,28（18）:36-41.Shen Guoqiao,Xu Dehong.Current control for grid-connected inverters by splitting the capacitor of LCL filter[J].Proceedings of the CSEE,2008,28（18）:36-41（in Chinese）.

[6]伍小杰,孙蔚,戴鹏,等.一种虚拟电阻并联电容有源阻尼法[J].电工技术学报,2010,25（10）:122-128.Wu Xiaojie,Sun Wei,Dai Peng,et al.An Active damping method of virtual resistor in parallel with capacitor[J].Transactions of China Electrotechnical Society,2010,25（10）:122-128（in Chinese）.

[7]Liserre M,Teodorescu R,Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Trans.on Power Electronics,2006,21（1）:263-272.

[8]Twining E,Holmes D.Grid current regulation of a threephase voltage source inverter with an LCL input filter[J].IEEE Trans.on Power Electronics,2003,18（3）:888-895.

[9]杭丽君,李宾,黄龙,等.一种可再生能源并网逆变器的多谐振PR电流控制技术[J].中国电机工程学报,2012,32（12）:51-58.Hang Lijun,Li Bin,Huang Long,et al.A multi-resonant PR current controller for grid-connected inverters in renewable energy systems[J].Proceedings of the CSEE,2012,32（12）:51-58（in Chinese）.

[10]鲍陈磊,阮新波,王学华,等.基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J].中国电机工程学报,2012,32（25）:133-142.Bao Chenlei,Ruan Xinbo,Wang Xuehua,et al.Design of grid-connected inverters with LCL filter based on pi regulator and capacitor current feedback active damping[J].Proceedings of the CSEE,2012,32（25）:133-142 （in Chinese）.

[11]Oetken G.A new approach for the design of digital interpolating filters[J].IEEE Trans.Acoust.Speech Signal Processing,1979,27（6）:637-643.

[12]Ye Y,Zhou K,Zhang B,et al.High performance repetitive control of PWM DC/AC converters with real-time phase-lead FIR filter[J].IEEE Trans.Circuits and SystemsⅡ,2006,53（8）:768-772