寄生电容对LLC谐振变换器的影响分析
2018-04-12徐志望董纪清
俞 珊,徐志望,董纪清
(1.福州大学至诚学院,福州 350002;2.福建睿能科技股份有限公司,福州 350003;3.福州大学电气工程与自动化学院,福州350116)
近年来,LLC谐振变换器由于具有电路拓扑简洁、可实现功率开关器件的软开关、易于实现磁集成和宽电压范围输入、变换效率和功率密度高等优点,成为业界的研究热点,并逐渐被应用于高频高效电能变换场合。
随着高频化应用的逐步深入,传统应用场合中可以被忽略的寄生参数开始参与LLC变换器的工作过程,从而影响变换器的性能指标[1]。寄生参数参与LLC变换器的工作过程中,通常伴随着高频谐振现象,会造成电磁干扰增大、可靠性与电磁兼容性降低等不良影响,甚至会影响变换器的正常工作[2]。设计人员可以通过优化LLC变换器高频变压器绕组布局的方式,充分利用高频变压器漏感作为谐振电感,从而实现磁集成,但是往往忽略了绕组分布电容对变换器性能的影响[3-7]。同时,作为变换器关键元件的功率半导体器件,如MOSFET和二极管等,由于器件制造工艺的缘故,也不可避免地存在寄生结电容。在分析这些寄生电容对LLC变换器影响的基础上,可以通过合理控制寄生电容的方法,或者提出一些改进型电路设计方法或控制策略,避免寄生电容对电路正常运行的不良影响,从而设计出性能优良的LLC变换器[8-9]。
本文从高频变压器分布电容的产生机理出发,在给出功率开关器件结电容的确定方法和高频变压器分布电容的相关改进措施的基础上,分析了分布电容对LLC变换器软开关过程的影响,并通过优化死区时间来提升变换效率[10-15]。同时,通过对考虑分布电容的LLC变换器的建模与仿真分析,得到新的输出电压增益表达式与电压增益曲线,揭示了LLC变换器在空载或轻载条件下电压增益失真机理,并提出一种新颖的双滞环自适应Burst控制策略。最后,本文制作了一台全数字化控制的LLC谐振变换器原理样机,并进行了相关实验验证。
1 寄生电容产生机理
假设LLC变换器功率电路的寄生电容主要包括:功率开关管 S1、S2的输出电容 C1、C2,整流二极管D1、D2的结电容Cj1、Cj2,以及高频变压器的分布电容 Cp、Cs1、Cs2和 Cps,如图1所示。其中,Cp和 Cs1、Cs2分别表示变压器原边和副边绕组的分布电容;Cps是原、副边绕组之间相互作用的电容。
高频变压器分布电容是由绕组层间以及匝间的静电场作用得到,其数值与变压器的结构和材质、绕组布局和绕法有关,并且和绕组空间中所存储的电场能量成正比。研究结果[1]表明,与层间的电场储能相比,同一层中相邻匝间的电场储能可以忽略,因此一般只考虑绕组层间的分布电容。
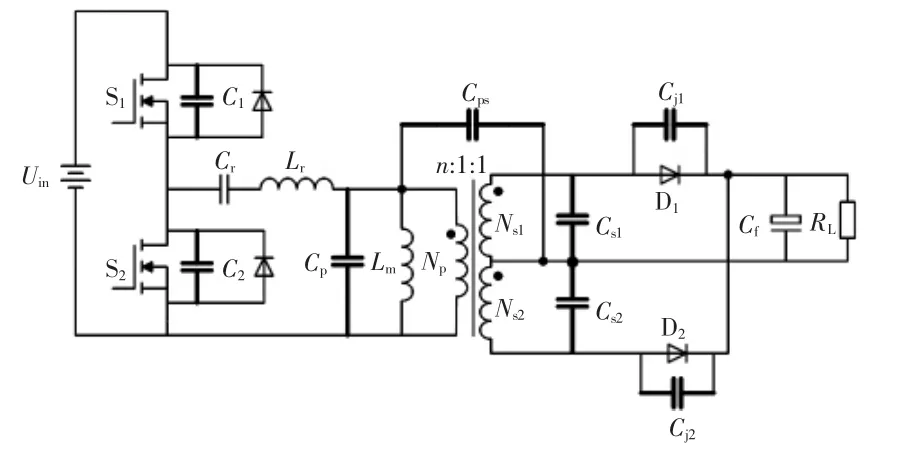
图1 考虑分布电容的LLC谐振变换器Fig.1 LLC resonant converter with distributed capacitance
高频变压器原边端口的幅频与相频特性可以通过阻抗分析仪扫频测量得到,并可在曲线拟合后通过谐振法进行阻抗分析。在分析频段内,若只出现1个谐振点,则可将绕组等效为一个R、L、C并联的模型;若出现3个谐振点,则可将绕组等效为两级R、L、C并联的形式,依此类推。变压器原边端口等效模型如图2所示。

图2 变压器原边端口等效模型Fig.2 Equivalent model of transformer primary port
本文以PQ26/25变压器为例进行寄生参数的建模分析。变压器的匝比Np:Ns1:Ns2=32:2:2,原边绕组采用0.1 mm×30的多股绞线,副边绕组采用12 mm×0.15 mm的铜箔,并按照图3所示的绕组分布方式进行绕制。其中,图(a)、(b)分别是U型与Z型两种原边绕组绕法的磁芯截面示意与绕组电压分布。
从图3可知,U型绕法简单,但绕组层间的最大电压差大,绕组端口等效电容大;Z型绕法稍复杂,但绕组层间的电压差减小,绕组端口等效电容也较小[2]。

图3 变压器采用不同绕法的绕组分布Fig.3 Distribution of different types of transformer windings
采用阻抗分析仪WK 6500B对上述变压器的原边绕组端口进行幅频、相频特性扫描,并采用两级模型等效建模计算出相关寄生参数,如表1所示。通过对图4所给出的实测值、计算值的幅频特性曲线的对比分析,验证了表1中寄生参数数值的正确性。

表1 变压器原边端口相关寄生参数Tab.1 Stray parameters of transformer primary port

图4 变压器原边端口阻抗幅频特性Fig.4 Amplitude-frequency characteristic of transformer primary port impedance
MOSFET和二极管等功率半导体器件,由于器件结构与制造工艺的缘故,不可避免地存在寄生结电容,其曲线如图5所示。功率MOSFET通常都采用输入电容Ciss、反馈电容Crss和输出电容Coss作为衡量MOSFET频率特性的参数,且这些电容并不是定值,而是随着其外部电路施加给MOSFET本身的电压变化的。以Infineon公司的SPP15N60CFD为例,MOSFET的寄生结电容随漏源极电压VDS变化的曲线,如图5(a)所示。
二极管由于存在势垒电容,其阻抗随着工作频率的增大而降低,因此存在最高的工作频率,即截止频率。二极管的结电容呈非线性,且随着外加反向电压变化而变化。以ON公司的肖特基二极管MBR60L45CTG为例,其结电容随反向电压VR变化的曲线,如图5(b)所示。肖特基二极管属于表面势垒二极管,是一种多数载流子导电器件,其反偏结电容数值不大,具备良好的频率特性,适用于工作低压大电流输出的高频应用场合。
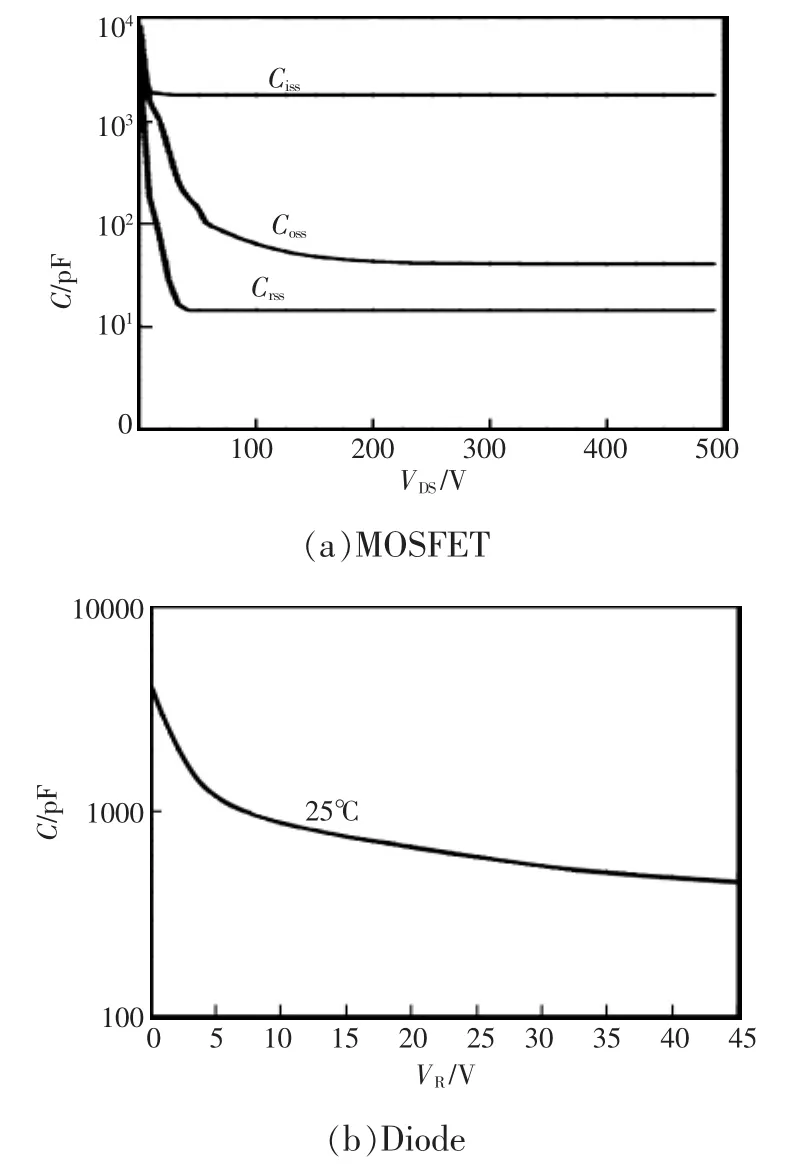
图5 功率半导体寄生电容曲线Fig.5 Stray capacitance curve of power semiconductor
2 寄生电容对软开关过程的影响
LLC变换器受业界青睐的重要原因是,通过合理的电路与控制参数设计,变换器可以在全负载范围内实现原边开关管的零电压开通ZVS(zero voltage switching)。
在原边开关管S1、S2切换的死区时间td内,励磁电流可近似看作一个电流源Im,并对原边开关管的输出结电容C1、C2和等效电容Ceq进行充放电,如图6所示。
忽略变压器原副边之间的寄生电容Cps,等效电容Ceq可近似表示为

式中:n为变压器原副边匝比;Cs为变压器副边绕组的分布电容,可以通过阻抗分析仪测量得到;Cj为副边整流二极管的结电容,可以通过查找数据手册,或如图5(b)所示的曲线得到。
LLC变换器要实现原边开关管的零电压开通,除了在电路参数设计上保证谐振网络呈感性外,还需要有足够长的死区时间td,来保证励磁电流能够对功率电路的寄生电容实现完全充放电。然而,死区时间td越大,通过谐振网络传递功率的有效时间越小;且在相同负载条件下,功率回路上的电流有效值相应增大,从而导致原边开关管的导通损耗与变压器的绕组损耗增加。

图6 在死区时间td内LLC变换器的等效电路Fig.6 Equivalent circuit of LLC converter in dead time td
因此,通过选择合适的死区时间td,可以在实现开关管ZVS的同时降低其导通损耗和变压器的绕组损耗,从而实现变换器效率的最优设计。
根据电荷守恒定理和基尔霍夫电流定律,LLC变换器实现原边开关管ZVS所需的最小死区时间td为
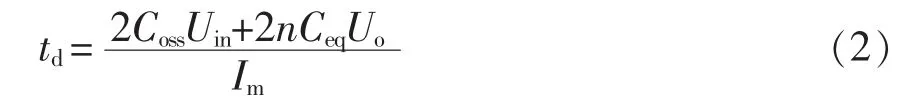
式中:Ceq为等效电容;Im为励磁电流;Uin为变换器输入电压;Uo为变换器输出电压。
由式(2)可知,等效寄生电容Ceq的存在影响着控制参数中死区时间的选择,从而影响变换器的软开关过程。依据输入电压Uin、输出电压Uo等,通过合理的电路设计与器件选型,得到变压器匝比n、励磁电流Im、原边开关管结电容Coss,再结合通过式(1)得到等效电容Ceq,从而确定合适的死区时间td。
3 寄生电容对输出电压增益的影响
LLC变换器中功率器件客观存在的寄生电容,将导致谐振网络元件参数的改变。对图1中考虑寄生电容的LLC变换器进行基波近似FHA(fundamental harmonic approximation)法分析[10],其等效电路如图7所示。

图7 考虑分布电容的LLC FHA等效电路Fig.7 FHA equivalent circuit of LLC with distributed capacitances
考虑等效分布电容Ceq的LLC变换器输出电压增益表达式为
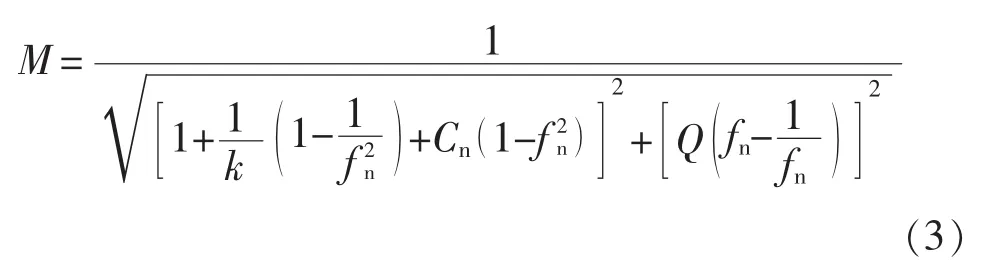
通过一个仿真实例分析寄生电容Ceq对输出电压增益的影响。根据经验参数,等效电容Ceq一般为皮法数量级,假设Ceq为500 pF,谐振电容Cr为30 nF,电感系数k为5,谐振频率fr为105 kHz。通过Mathcad软件,得到不同负载品质因数Q下的增益曲线;通过Saber仿真软件对LLC进行小信号仿真分析,得到的输出电压增益曲线如图8所示。
由图8可知,由于分布电容的存在,使LLC变换器输出电压增益曲线新增1个由谐振电感Lr和分布电容Ceq构成的谐振频率点,从而使得LLC在相对高频工作条件下出现输出电压增益失真,导致在空载或轻载条件下,LLC变换器会因为没有合适的闭环工作频率点导致其输出电压出现不稳定或过压失控等现象。
解决LLC变换器在空载或轻载运行时出现输出电压增益失真问题的方法有4种:①增加假负载使Q值增大。Q值增大,则LLC在运行时所需的开关频率被限制在增益失真的频率之前,从而抑制了寄生电容带来的影响。但该方法并不适用于对待机损耗或者效率变换要求严格的应用场合。②降低分布电容Ceq使寄生谐振频率增大。通过合理设计变压器以及器件严格选型,可以在一定程度上降低分布电容,但这并不能完全消除分布电容的影响。③增大电感系数k。在相同的谐振频率和励磁电感条件下,增大k值,则谐振电感Lr会减小,从而使寄生谐振频率增大。但在需要LLC实现宽范围电压输入的应用场合,磁性元件参数的设计将因此受到较大的限制。④Burst控制模式。采用在PWM型变换器常用的间歇式控制模式,即Burst模式,如图9所示。但该模式存在以下缺陷:驱动信号时有时无,引入了低频分量,使输出电压纹波较大;LLC变换器若没有引入合适的控制逻辑,不仅不能提高电路轻载时的变换效率,反而会导致器件瞬间过流保护,甚至故障并损坏。
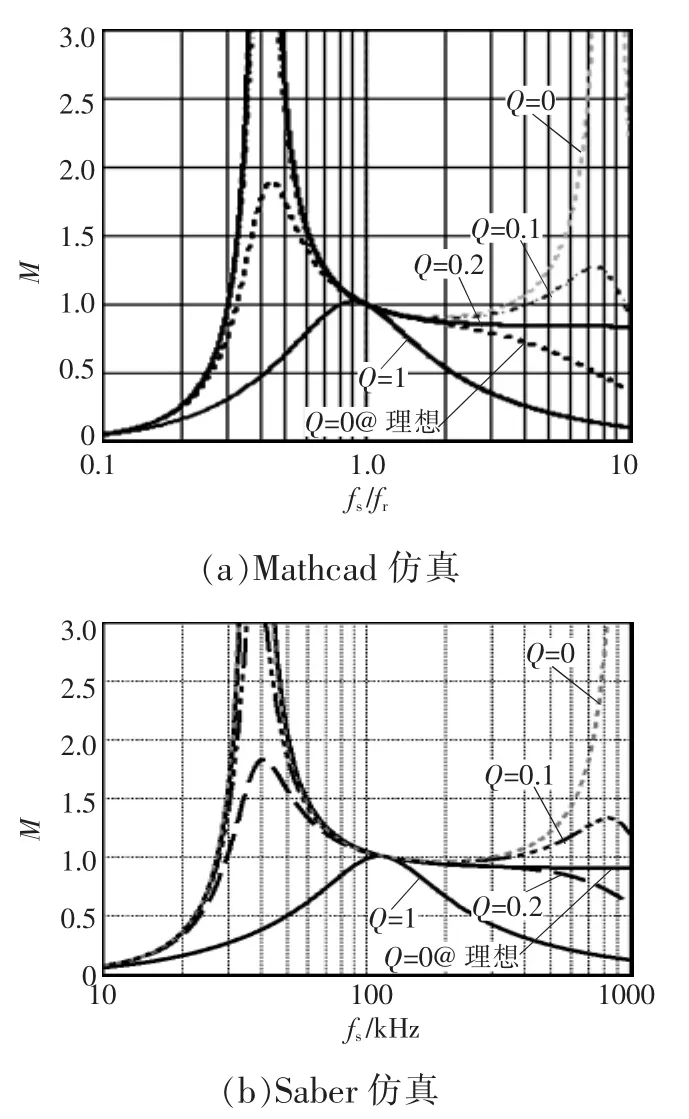
图8 LLC输出电压增益仿真曲线Fig.8 Simulation of LLC output voltage gain curves
4 控制策略与实验验证
LLC变换器中功率器件的寄生电容客观存在,针对LLC变换器在空载或轻载下存在的输出电压增益失真问题,文献[13,14]提出了一种基于最佳效率点的Burst控制方案。该方案在Burst控制模式的Ton时段内,施加一个通过测试得到的变换器最优效率所对应的固定频率,以实现Burst模式下的效率优化。然而,在恒定的周期内TBurst,当负载加重,Ton会随之增加,从而导致输出电压纹波变大。文献[14]通过保持Burst导通时间Ton恒定,根据负载大小来调整关断时间Toff,从而使得输出电压纹波与负载情况无关,但却不能实现Burst工作模式下的效率优化。
本文提出一种新颖的双滞环自适应Burst控制策略,如图9所示。由图可见,随着负载电流Io降低至IoB时,LLC变换器通过闭环PFM控制方式已无法得到合适的闭环工作频率点,当输出电压Uo逐步升高至电压纹波要求上限Uom时,控制芯片关闭驱动信号;当Uo逐步降低至Burst控制的电压滞环下限UoL时,启动驱动脉冲信号,施加的开关频率为谐振频率fr;当Uo升至电压滞环上限UoH时,再次关闭驱动信号;如此往复,直到负载Io增加使得输出电压Uo降低至电压纹波要求下限Uon,变换器回到闭环PFM控制模式。
该控制策略在Burst控制模式的Ton时间内施加谐振频率fr的驱动信号,使LLC在每个Burst开关周期内只有最先开通的开关管是硬开关开通,之后的每个开关周期均可实现软开关,从而实现了效率的优化;同时,通过采用输出电压纹波双滞环限定逻辑(Uom↔Uon、UoH↔UoL),可在全负载范围内将输出电压纹波的稳态与动态指标限定在工程要求范围之内。

图9 双滞环自适应Burst控制示意Fig.9 Schematic of dual hysteresis adaptive Burst control
本文制作完成了一台240 W全数字控制半桥LLC谐振变换器的样机。样机的基本电气参数如下:输入电压Uin为350~400 VDC,额定输出为12 V/20 A,谐振频率fr为105 kHz,电感系数k为9,高频变压器匝比Np:Ns1:Ns2为32:2:2,绕组布局采用Z型绕法。样机的关键电路元件型号如表2所示。

表2 LLC样机关键电路元件列表Tab.2 List of key circuit components in LLC prototype
图10给出了LLC变换器工作于空载Io=0 A时关键波形。其中,输出电压纹波△Uo的峰峰值为106 mV,满足样机±0.5%的电压纹波稳态要求。

图10 空载下输出电压纹波波形Fig.10 Waveform of output voltage ripple under no load
图11给出了LLC谐振变换器在额定输入电压Uin=400 V下的效率对比曲线。其中,针对闭环变频控制和双滞环自适应Burst控制两种控制模式在10%及以下负载进行效率对比。
从图11所示的实验结果可知,通过对死区时间的优化调整,LLC谐振变换器在全负载范围均可实现高效率。同时,本文所提出的双滞环自适应Burst控制策略,还可进一步显著提高变换器轻载下的变换效率,在2.5%负载下的效率甚至可达到90.23%。
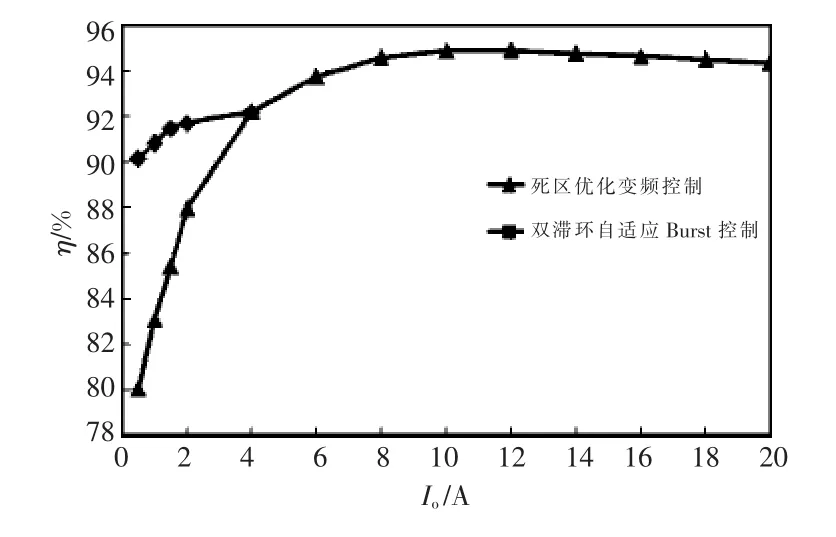
图11 LLC变换器样机效率对比Fig.11 Comparison of efficiency of LLC converter prototype
5 结语
在全面分析研究寄生参数对LLC变换器影响的基础上,通过掌握合理控制寄生参数的方法,减轻寄生参数对电路正常运行的不良影响;甚至可以充分利用某些寄生参数的固有特性,设计出性能优良的变换器。
参考文献:
[1]赵志英,龚春英,秦海鸿.高频变压器分布电容的影响因素分析[J].中国电机工程学报,2008,28(9):55-60.Zhao Zhiying,Gong Chunying,Qin Haihong.Effect factors on stray capacitances in high frequency transformers[J].Proceedings of the CSEE,2008,28(9):55-60(in Chinese).
[2]董纪清,陈为,卢增艺.开关电源高频变压器电容效应建模与分析[J].中国电机工程学报,2007,27(31):121-126.Dong Jiqing,Chen Wei,Lu Zengyi.Modeling and analysis of capacitive effects in high-frequency transformer of SMPS[J].Proceedings of the CSEE,2007,27(31):121-126(in Chinese).
[3]李旭升,张岱南,岑凯妮,等.磁集成LLC谐振变换器的设计[J].磁性材料及器件,2014,43(4):44-48.Li Xusheng,Zhang Dainan,Cen Kaini,et al.Design of magnetically integrated LLC resonant converter[J].Joural of Magnetic Materials and Devices,2014,43(4):44-48(in Chinese).
[4]Kang B G,Park C S,Chung S K.Integrated transformer using magnetic sheet for LLC resonant converter[J].Elect-ronics Letters,2014,50(10):770-771.
[5]Zhang Juyong,Hurley W G,Wolfle W H.Design of the planar transformer in LLC resonant converters for microgrid applications[C].IEEE 5th International Symposium on PowerElectronics forDistributed Generation System(PEDG).Galway,Ireland,2014:1-7.
[6]De Simone S,Adragna C,Spini C.Design guideline for magnetic integration in LLC resonant converters[C].2008 International Symposium on Power Electronics,Electrical Drives,Automation and Motion,Ischia,Italy.IEEE,2008:950-957.
[7]Zhang Jun,Hurley W G,Wolfle W H,et al.Optimized de-sign of LLC resonant converters incorporating planar magnetics[C].2013 Twenty-Eight Annual IEEE Applied Power Electronics Conference and Exposition(APEC).Long Beach,CA,USA,2013:1683-1688.
[8]Halberstadt H.Method of operating a resonant power converter and a controller therefore:U.S.2011/000 2145 A1[P].2011-01-06.
[9]Khoobroo E,Ashrafinia B,Akhbari M.Optimal design of LLC resonant converter with improved controllability[C].Power Electronics,Drive Systems and Technologies Conference(PEDSTC).Tehran,Iran,2014:396-401.
[10]Fang Xiang,Hu Haibing,Chen F,et al.Efficiency-oriented optimal design of the LLC resonant converter based on peak gain placement[J].IEEE Transactions on Power Electronics,2013,28(5):2285-2296.
[11]Yang C H,Liang T J,Chen Kaihui,et al.Loss analysis of half-bridge LLC resonant converter[C].International Future EnergyElectronicsConference(IFEEC).Tainan,China,2013:155-160.
[12]Feng Weiyi,Lee F C,Mattavelli P.Optimal trajectory control of Burst mode for LLC resonant converter[J].IEEE Transactions on Power Electronics,2013,28(1):457-466.
[13]Wang Bin,Xin Xiaoni,Wu S,et al.Analysis and implementation of LLC Burst mode for light load efficiency improvement[C].IEEE Applied Power Electronics Conference&Exposition,2009:58-64.
[14]Jang Y,Jovanovic M M.Light-load efficiency optimization method[J].IEEE Transactions on Power Electronics,2010,25(1):67-74.
[15]Ye Yiqing,Yan Chao,Zeng Jianhong,et al.A novel light load solution for LLC series resonant converter[C].IEEE Pro.INTELEC 2007,International Telecommunications Energy Conference.Rome,Italy,2007:61-65.
