VIENNA整流器的设计与优化
2018-04-12曹丰文李武华何湘宁
刘 源 ,梅 烨 ,曹丰文 ,李武华 ,何湘宁
(1.浙江大学电气工程学院,杭州 310027;2.苏州职业大学电子信息工程系,苏州 215104)
为了满足日益增长的用电需求并且适应复杂多变的用电场合,大量的电力电子装置获得了广泛的应用[1]。为了解决电网三相交流供电与大量电子设备直流供电之间的矛盾,三相AC/DC整流器成为很多用电场合下电力电子设备中不可或缺的电气环节[2]。传统二极管整流器和相控整流器的网侧输入电流含有大量低次谐波,是电网谐波的最主要来源。有资料表明[3],在电力用户中,最大谐波源为电力电子装置用户的占比为90%,而其中最大谐波源为整流器的用户占89%。大量低次谐波造成了电网电能质量下降,进一步影响电网稳定性。所以,降低三相AC/DC整流器的输入电流谐波含量具有重要意义。
抑制三相AC/DC整流器输入电流谐波的一种方法是用普通桥式PWM整流器代替传统整流器。与传统整流器相比,PWM整流器具有网侧输入电流谐波含量低的特点,能够实现单位功率因数运行且直流侧电压可控。但其主要缺点是需要较多功率开关器件,尤其是在实现更多电平输出的情况下所需功率器件更多。针对此问题,Kolar教授于1994年提出了VIENNA整流器[4],VIENNA整流器进一步减小了功率开关数量,提高了功率密度,同时对大多现有的功率因数校正PFC(power factor correction)控制方法有良好适应性[5-7]。VIENNA整流器是基于三电平拓扑,具有开关应力小、输入电流总谐波失真度 THD(total harmonic distortion)低、结构简单等优点,广泛应用于微网、风能发电、功率因数校正和有源滤波器等场合[8-11]。
当电网电压含有低次谐波时,VIENNA整流器网侧输入电流亦会含有相应次数谐波,造成电网电能质量下降,严重时影响设备安全可靠运行。电网电压前馈是一种常用的谐波抑制方法[12-13]。文献[12]建立了电网电压前馈在数字控制下的物理模型,其可以等效为一个阻尼电阻加上电抗和滤波电容并联的结构,并分析了不同频率下的阻尼特性;文献[13]提出了一种含电网电压比例、微分以及二阶微分的前馈方法,但引入电网电压前馈环节在提高系统动态性能和谐波抑制的同时,降低了系统稳定性。针对上述方法的不足,本文采用了一种结合VIENNA整流器具体控制环路的指定次谐波优化方法。该方法首先在谐波旋转坐标系下提取指定次谐波分量,继而通过谐波闭环的方法实现指定次谐波消除。
本文首先简要介绍VIENNA整流器工作原理,并结合3 kW系统进行了相应的工程设计,主要包括储能元件设计、滤波环节设计和控制环路设计。针对电网电压畸变带来的输入电流谐波问题,采用了一种结合VIENNA整流器具体控制环路的指定次谐波优化方法。针对LCL滤波器带来的谐振问题,从工程设计的角度进行了相应优化。最后根据工程设计得到的具体参数搭建了3 kW实验平台并进行了工程设计和优化方法的有效性验证。
1 VIENNA电路结构和原理
VIENNA整流器主电路拓扑由工作在Boost模式下的3个升压电感、3个双向功率开关、2个直流侧电容以及6个整流二极管组成。每个双向功率开关由2个开关管通过共源级串联组成。将双向功率开关用理想开关替代,可以得到VIENNA整流器简化拓,扑如图1所示。
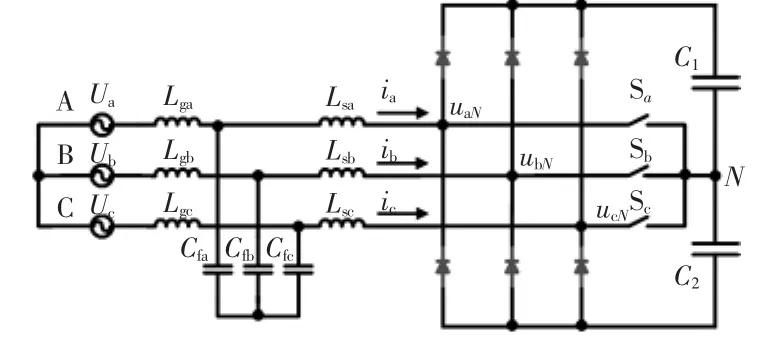
图1 VIENNA整流器拓扑示意Fig.1 Topology of VIENNA rectifier
VIENNA整流器工作时,桥臂工作状态由输入电流ia方向决定。以A相为例,当ia>0且开关Sa闭合时,电流从电感 Lsa流入中点 N,uaN=0;当 ia>0且开Sa关断开时,电流从A相电感Lsa经过上桥臂二极管流入电容 C1,uaN=Vc1;当 ia<0 且开关 Sa闭合时,电流从中点N流入电感Lsa,uaN=0;当ia<0且开关Sa断开时,电流从C2经过下桥臂二极管流入电感Lsa,uaN=-Vc2。
由上述分析可知,当某相电流大于0时,通过控制对应开关管的导通/关断,来实现对应相电流增加/减小;电流小于0时情况则相反。通过控制开关管的开通关断,可实现控制每相电流为正弦波,从而保持直流侧电压恒定。
2 VIENNA整流器工程设计
本文结合实际工程应用,对3 kW VIENNA整流器进行详细的工程设计,主要包括储能元件设计、滤波环节设计和控制环路设计。系统通过三相电网输入,输出电压为630 V,开关频率为20 kHz,其余技术指标如表1所示。

表1 3 kW VIENNA整流器系统技术指标Tab.1 Technical indexes of 3 kW VIENNA rectifier system
2.1 直流侧电容设计
(1)考虑直流侧电压跟随性能(包括上升时间、峰值时间、调节时间和超调量)时,讨论其从稳态值跃变到额定值的动态过程对电容参数设计的要求。
电压指令给定为额定电压时,在电压达到额定直流电压前,电压环处于饱和状态。整流器直流侧将以最大电流对电容和负载充电,其等效电路如图2所示。

图2 母线电容充电等效电路Fig.2 Equivalent circuit of capacitor charging
PFC未启动时,电网通过三相不控整流给负载供电,母线电压平均值为

式中,E为电网线电压有效值。根据图2解得直流侧电压表达式为

令uC=Vde,其中Vde为额定直流电压,将其代入式(2),解得

要求直流侧电压从稳态值Vdo上升到额定值Vde的上升时间不大于tr,即

工程上常取Idm和Vde[14]为

将式(1)和式(5)代入式(4),可得

(2)考虑直流侧电压抗干扰性能(包括动态降落、恢复时间)时,以空载切到额定负载时电压的动态过程来讨论对电容参数设计的要求。
空载切到额定负载时,母线电压跌落,电压环处于饱和状态,考虑电流内环惯性,直流侧电流将渐变至Idm。为简化分析,令直流侧电流对时间的函数为

式中,Ti为电流内环惯性时间常数。

图3 加载时等效电路Fig.3 Equivalent circuit from zero to full load
电容电压初始值为Vde,根据图3解得电容电压表达式为


工程上常取Idm和ReC[14]为

将式(10)代入式(9),可得 t≈0.8Ti。直流电压最大动态降落为

式(11)可以化为

将式(10)代入式(13),可得电容下限值为

根据式(6)和式(14)计算出电容上限值为500 μF,下限值为150 μF。综合考虑跟随性能和抗干扰性能后,电容取值为330 μF。为提高耐压能力,由4个330 μF/400 V电容两串两并组成。
2.2 LCL滤波器设计
LCL滤波器结构如图4所示。其桥臂电压对网侧输入电流的传递函数为

整流器稳定运行时交流侧各矢量关系如图5所示(忽略电感寄生电阻)。其中,I为交流侧电流,V为整流器交流侧电压,L为交流侧电感Lg、Ls之和,VL为交流侧总电感电压,φ为功率因数角。当E、I的有效值恒定时,V的轨迹为图5中的圆周。

图4 LCL滤波器结构Fig.4 Structure of LCL filter

图5 VIENNA整流器交流侧矢量关系Fig.5 Vector diagram of VIENNA rectifier on AC side
对于图5三角形OO1T,由余弦定理可得

式中 ,Vm、Em分别为VIENNA整流器交流侧基波相电压峰值和电网电动势峰值。由Po=3EmImcosφ/2和Qo=3EmImsinφ/2可得

对于三相整流器,有

式中,M为PWM相电压最大利用率,SPWM控制下M=1/2;SVPWM控制下。
将式(19)代入式(17)、(18)可得
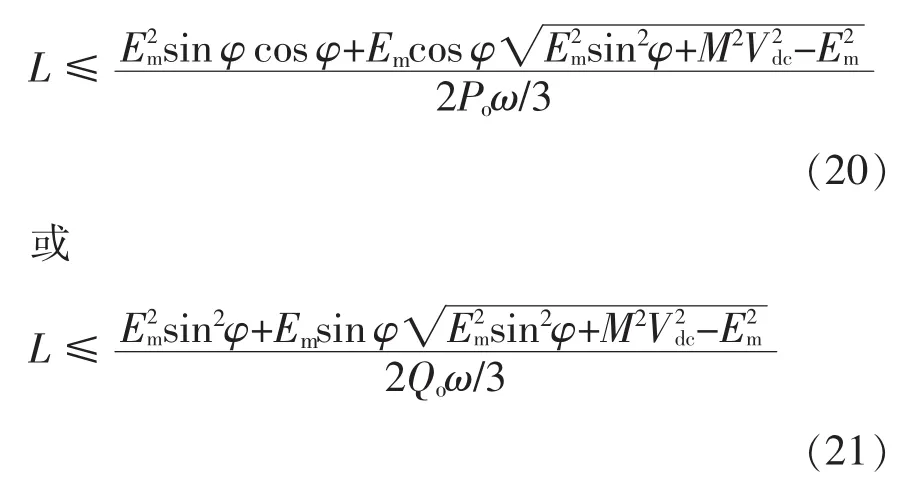
当整流器运行在单位功率因数状态(φ=0)且采用SVPWM控制时,有
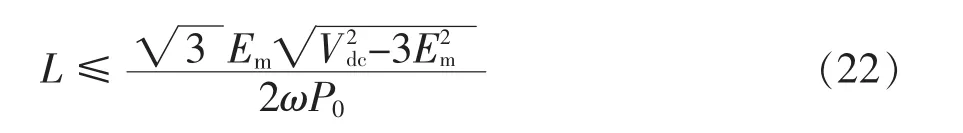
电容的无功功率一般限制在5%内,即有

式中,Vc为滤波电容电压有效值,可近似为电网电压。按照上述计算,选取电容为1 μF。
考虑到对最大电流纹波幅值的要求,整流器交流侧电感可确定[14]为

经过计算,交流测电感Ls下限值为5 mH,结合式(22)且留取一定裕量,电感取为7.5 mH。
根据网侧到整流器交流侧n次开关频率谐波电流衰减公式可确定网侧电感[14]为

经过上述计算,网侧电感取值1.2 mH。
LCL滤波器一般要求谐振频率在10倍工频和0.5倍开关频率之间,即

经验证,Lg=1.2 mH,Ls=7.5 mH,C=1 μF 时谐振频率为 4.78 kHz,满足式(26)的要求。
2.3 控制系统设计
(1)VIENNA整流器拓扑交流侧dq模型可描述为
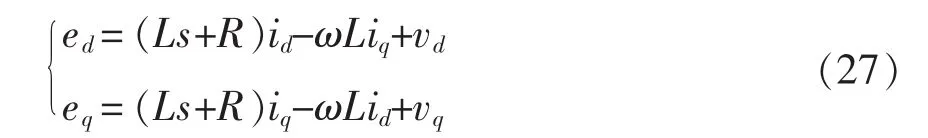
式中:ed、eq为电网电动势 d、q 分量;vd、vq为 VIENNA整流器交流侧电压d、q分量;R为电感寄生电阻。
采用前馈解耦控制策略[15],vd、vq控制方程变为

式中:Kip、KiI为电流控制器 PI参数;idref、iqref为电流指令值。
将式(28)代入式(27),并考虑电流采样延迟和PWM控制小惯性特性并忽略电网电压扰动,可得电流环简化结构,如图6所示。图中,Ts为采样周期;KPWM为桥路等效增益。

图6 电流环简化结构Fig.6 Simplified structure of current loop
为使电流内环获得较快的跟随性能(包括上升时间、峰值时间、调节时间、超调量),以PI调节器零点抵消电流控制对象传递函数极点,即τi=L/R。按典型I型系统参数整定关系[16],取系统阻尼比ξ=0.707,有

经计算,电流环PI参数为Kip=50,KiI=600。
根据式(29)和图6,电流内环闭环传递函数可简化为

式(30)可近似等效为时间常数为3Ts的惯性环节,当开关频率较高时具有良好的动态响应。
(2)VIENNA整流器拓扑直流侧dq模型可描述为
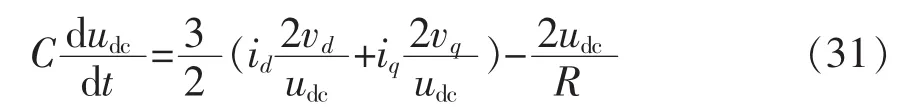

图7 电压环简化结构Fig.7 Simplified structure of voltage loop
由图7可得电压环开环传递函数为

电压外环的主要作用是稳定直流电压,应着重考虑其抗干扰性能。由Ⅱ型系统控制器参数的整定关系[17]可得

式中,hv为频带宽,,代入式(33),得到电压环PI参数为

经计算,电压环 PI参数为 Kv=1.32,τv=0.001。
3 输入电流谐波抑制及LCL滤波器优化
当电网电压含有低次谐波时,VIENNA整流器输入电流亦会含有相应的低次谐波,降低了VIENNA整流器的功率因数,严重时可引起滤波电容和电感的过载,给设备带来了安全隐患。按照第2节VIENNA整流器工程设计中的参数设计,在Matlab/Simulink平台上搭建了3 kW VIENNA系统,其电网电压畸变时的输入电流波形对比如图8所示。对图8(b)中的电流波形进行快速傅里叶变换FFT(fast Fourier transformation),相应结果如图8(c)所示。

图8 VIENNA整流器输入电流仿真波形和频谱图Fig.8 Waveform and spectrogram of input current
3.1 VIENNA整流器输入电流谐波优化
针对上述问题,本文采用了一种消除指定次谐波电流方法以优化输入电流THD,该方法应用于VIENNA整流器中,其控制框图如图9所示。

图9 具有输入电流优化功能的VIENNA整流器控制框图Fig.9 Control block diagram of VIENNA rectifier with input current optimization
指定次谐波电流消除流程如下:
(1) 对 ia、ib、ic进行 Clark 变换和谐波坐标系下的Park变换(三相谐波为正序,相位取nθ;负序时则相反),得到n次谐波电流在谐波旋转坐标系下的d、q轴分量,并经过低通滤波器LPF(low pass filter)后作为谐波电流环的反馈值。
(2)谐波电流环输出通过谐波旋转坐标系下的Park逆变换和基波旋转坐标系下的Park变换,得到谐波电流在基波旋转坐标系下的指令值和。
(3)将谐波电流在基波坐标系下的指令值叠加到基波电流环的指令值中,即可实现n次谐波电流消除。
根据上述方法设计实际控制系统。VIENNA整流器谐波旋转坐标系下的数学模型为

式中,edn、eqn为电网电动势 n 次谐波 d、q 分量;vdn、vqn为VIENNA整流器交流侧n次谐波电压d、q分量;idn、iqn为 n 次谐波电流 d、q 分量。
将VIENNA整流器中各次谐波转化到基波坐标系下进行解[18],可得


图10 谐波电流环简化结构Fig.10 Simplified structure of harmonic current loop
为使谐波环获得较快的跟随性能,以PI调节器零点抵消电流控制对象极点,即τins=L/R。按典型I型系统参数整定关系[16],取系统阻尼比ξ=0.707,则有

根据式(37)并结合谐波次数,可以计算KinP、KinI具体值。
3.2 LCL滤波器谐振问题优化
为抑制LCL滤波器谐振特性以提高系统稳定性,用电容支路串电阻方案增加系统阻尼。引入阻尼电阻后,LCL滤波器桥臂电压对网侧输入电流的传递函数为

由图11可得,增大阻尼电阻Rd能够降低谐振尖峰并提高系统稳定性,但随着阻尼电阻的增大,会带来较大的系统损耗与较差的高频滤波特性。综合考虑系统稳定性、损耗及滤波性能,实际工程应用中取阻尼电阻为谐振频率处滤波电容容抗的1/3,即

当阻尼电阻为谐振频率处滤波电容C容抗的1/3时,低频段下LCL的幅频特性基本不受影响,高频段下衰减速率受到一定影响,但开关频率处产生的影响在允许的范围内。

图11 LCL滤波器的幅频特性曲线Fig.11 Amplitude-frequency curves of LCL filter
4 实验验证
本文搭建了3 kW实验平台进行了工程设计和优化方法的有效性验证。具体元件参数如表2所示,二极管选用CREE公司的碳化硅肖特基二极管C4D20120A,开关管选用英飞凌公司的MOSFET IPA65R045C7。相关数字控制在TI公司的TMS320 F28069上实现。

表2 实验元器件及相关参数Tab.2 Experimental components and the related parameters
半载工况下输入电流波形及其频谱如图12所示。在输入电压畸变情况下,A相输入电流优化前波形如图12(a)所示;采用所提谐波消除方法后,A相输入电流波形如图12(b)所示;为了更直观地对比谐波消除的效果,对图12(a)、(b)中的电流波形进行快速傅里叶变换,相应结果如图12(c)所示。
由图可见,优化前半载工况下输入电流THD为4.6%,13次谐波含量为3%。采用指定次谐波消除法后,半载工况下输入电流THD为3.4%,13次谐波含量为0.4%。与优化前相比13次谐波降低了83%,有效地抑制了13次谐波。

图12 半载工况下输入电流波形和频谱Fig.12 Waveform and spectrogram of input current in half load
5 结语
本文结合实际工程应用对3 kW VIENNA系统进行了具体的工程设计,主要包括储能元件设计、滤波环节设计和控制环路设计。针对输入电压畸变引起的输入电流谐波问题采用了一种结合VIENNA整流器具体控制环路的指定次谐波优化方法并对其中谐波环进行了相应设计。根据工程设计得到的具体参数搭建了3 kW实验平台并进行了工程设计和谐波优化方法的有效性验证。实验结果表明,采用的输入电流指定次谐波优化方法具有显著的指定次谐波消除能力,能有效改善输入电流畸变。
参考文献:
[1]钱照明,张军明,吕征宇,等.我国电力电子与电力传动面临的挑战与机遇[J].电工技术学报,2004,19(8):10-21.Qian Zhaoming,Zhang Junming,Lü Zhengyu,et al.Challenge and opportunity for power electronics and electrical drive in China[J].Transactions of China Electrotechnical Society,2004,19(8):10-21(in Chinese).
[2]Kolar J W,Friedli T.The essence of three-phase PFC rectifier systems[C]//2011 IEEE 33rd International Telecommunications Energy Conference(INTELEC).Amsterdan,Nethelands,2011:1-27.
[3]王兆安,杨军,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2016:1-6,36-37.
[4]Kolar J W,Zach Franz C.A novel three-phase utility interface minimizing line current harmonics of high-power telecommunications rectifier modules[C]//The 16th International Telecommunications Energy Conference.Vancouver,Canada,1994:367-374.
[5]王正,谭国俊,曾维俊,等.基于SVPWM的VIENNA整流器研究[J].电气传动,2011,41(4):31-34.Wang Zheng,Tan Guojun,Zeng Weijun,et al.Study on the VIENNA rectifier based on space vector pulse width modulation[J].Electric Drive,2011,41(4):31-34(in Chinese).
[6]Hang Lijun,Li Bin,Zhang Ming,et al.Equivalence of SVM and carrier-based pwm in three phase/wire/level vienna rectifier and capability of unbalanced-load control[J].IEEE Transactions on Industrial Electronics,2014,61(1):20-28.
[7]Lee J,Lee K.Carrier-based discontinuous PWM method for vienna rectifiers[J].IEEE Transactions on Power Electronics,2015,30(6):2896-2900.
[8]Rajaei A,Mohamadian M,Varjani A.Vienna-rectifier-based direct torque control of PMSG for wind energy application[J].IEEE Transactions on Industrial Electronics,2013,60(7):2919-2929.
[9]Chen Hao,David N,Aliprantis D C.Analysis of permanentmagnet synchronous generator with vienna rectifier for wind energy conversion system[J].IEEE Transactions on Sustainable Energy,2013,4(1):154-163.
[10]Kedjar B,Kanaan H Y,Al-Haddad K.Vienna rectifier with power quality added function[J].IEEE Transactions on Industrial Electronics,2014,61(8):3847-3856.
[11]Hang Lijun,Zhang Ming,Tolbert L M,et al.Digitized feedforward compensation method for high-power-density three-phase vienna PFC converter[J].IEEE Transactions on Industrial Electronics,2013,60(4):1512-1519.
[12]Lu Minghui,Wang Xiongfei,Blaabjerg F,et al.Grid-voltage-feedforward active damping for grid-connected inverter with LCL filter[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC).Long Beach,USA,2016:1941-1946.
[13]Wang Xuehua,Ruan Xinbo,Liu Shangwei,et al.Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics[J].IEEE Transactions on Power Electronics,2010,25(12):3119-3127.
[14]张兴,张崇巍.PWM整流器及其控制[M].北京:机械工业出版社,2012:89-93,97-99,106-117,254-281.
[15]Ye Y,Kazerani M,Quintana V H.A novel modeling and control method for three-phase PWM converters[C]//2001 IEEE 32nd An-nual Power Electronics Specialists Conference.Vancouver,Canada,2001,1:102-107.
[16]Dahono P A,Bahar Y R,Sato Y,et al.Damping of transient oscillations on the output LC filter of PWM Inverters by using a Virtual Resistor[C]//4th IEEE International Conferen-ce on Power Electronics and Drive System.Denpasar,Indonesia,2001,1:403-407.
[17]王孝武.现代控制理论基础[M].北京:机械工业出版社,1998.
[18]张树全,戴珂,谢斌,等.多同步旋转坐标系下指定次谐波电流控制[J].中国电机工程学报,2010,30(3):55-62.Zhang Shuquan,Dai Ke,Xie Bin,et al.Selective harmonic current control based on multiple synchronous rotating coordinates[J].Proceedings of the CSEE,2010,30(3):55-62(in Chinese).
