基于比例积分谐振的微网逆变器电压均衡控制策略研究

张梦帆，傅明月，陈 新

（南京航空航天大学自动化学院 ，南京 211106）

分布式发电 DG（distributed generation）[1-4]是相对传统集中式发电而言的独立发电系统，有着便携、绿色和可靠性高等优点，分布式发电系统的发展促进了微电网的发展。为了使微电网的应用更加灵活与高效，能在离网和并网两种状态下平稳工作和切换成为了基本的要求。为减少并网时对电网的暂态冲击，以及保证本地重要负荷的供电质量，两种模式间平滑切换的能力是保证微电网可靠运行的关键技术[5-7]；同时随着负载用电密度的迅速增加和对电能质量敏感的用电设备的不断普及，用户对电网运行的可靠性和电能的质量要求越来越高，但是工作在离网模式的微网逆变器又常常会工作在三相负载不平衡的情况。三相负载不平衡不仅会引起电压波动、闪变，同时还会给系统注入大量高次谐波，严重影响电能质量，危害用户供电安全[8]，因此抑制系统输出不平衡问题也是微电网可靠运行的关键问题。

本文针对在离网模式下带不平衡负载的微电网应用的场合，采用应用分裂电容的三相四线逆变器拓扑，提取输出的正负序分量分别进行控制，抑制负序分量，同时采用空间矢量调制SVM（space vector modulation）进行调制以抑制零序分量，从而实现输出电压平衡。同时针对传统主从结构的微电网模式切换中存在的缺陷，本文研究了采用间接电流控制的平滑切换控制策略，保证了无论在离网和并网模式，逆变器始终按照电压源型模式运行，从而避免了控制器切换带来的问题。最后，在15 kVA微电网逆变器实验平台上，通过实验验证了该方案的实用性和可行性。

1 不平衡负载系统的模型

为了简化分析，将带不平衡负载工作的逆变器系统的模型分为离网运行模式和在离网与并网双模式切换两个状态进行建模分析。

1.1 离网状态下带不平衡负载运行

图1所示为应用分裂电容的三相四线逆变器工作在离网模式下的拓扑，其中Z为本地负载，ua、ub、uc为电容电压，ua0、ub0、uc0为逆变器输出电压。

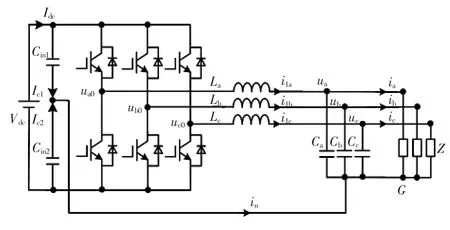
图1 应用分裂电容的三相四线逆变器的拓扑Fig.1 Topology of three-phase four-wire inverter with split capacitor

为了方便分析，可以对模型进行简化，三相四线制逆变器的等效模型[9-11]，如图2所示。

以 A 相为例，Rs为逆变器负载电阻，ia、ib、ic为逆变器输出电流，则有

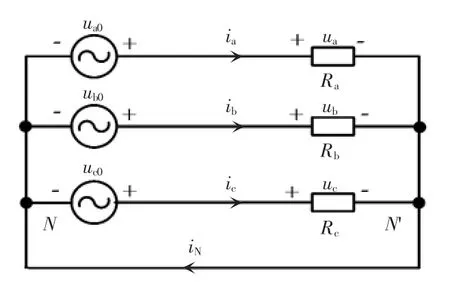
图2 逆变器等效电路模型Fig.2 Equivalent circuit of inverter

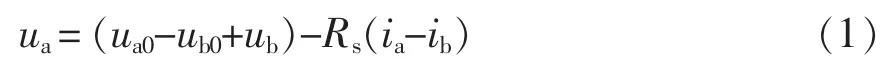
由此可见，三相之间输出不独立。依据对称分量法可知，任意一组不平衡的三相向量可以分解出正序分量、负序分量和零序分量，不考虑谐波，不平衡电压可以表述为

在正序分量的同步旋转坐标系下将式（2）进行Park变换，可得

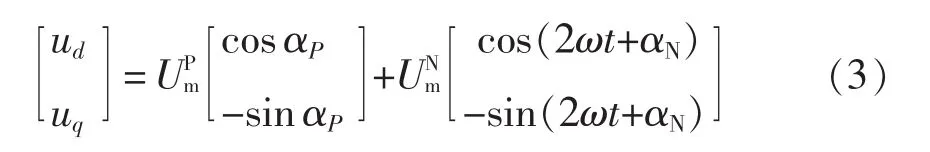
从式（3）可以看出，正序分量变为直流量，而负序分量变为2倍频的交流量。采用比例积分控制交流量的性能较差，所以常规的比例积分电压电流双闭环控制并不能达到较好的效果，需要采用比例积分谐振 PIR（proportional integral resonance）的方案对负序分量进行控制[12-15]。

1.2 离网和并网模式切换运行

针对上文提到的问题对并网模式和离网模式之间切换时产生的电压电流冲击进行建模分析。在微电网逆变器并网时三相电压被电网电压钳位，所以三相电压对称，以其中一相为例得到如图3所示的系统的简化框图。图中：Z0为逆变器输出阻抗，Zg为电网阻抗，Zload为本地负载，io为逆变器输出电流，ig为并网电流。

当系统并网运行时，由于Zg较小，负载两端电压u1近似等于电网电压，即

当系统离网运行时，负载两端电压u2为逆变器输出电压，即

因此可以得到模式切换时的电压突变量为

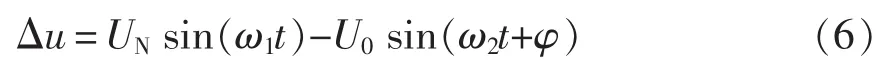
由此产生的电流突变为

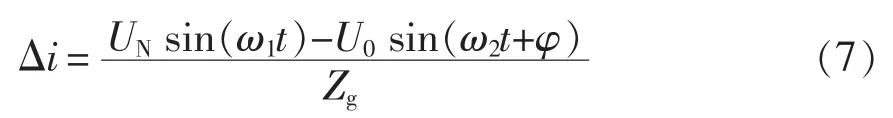
由于Zg较小，当模式切换前后逆变器输出端电压的频率、相位和幅值不一致时便会产生较大的电流冲击。

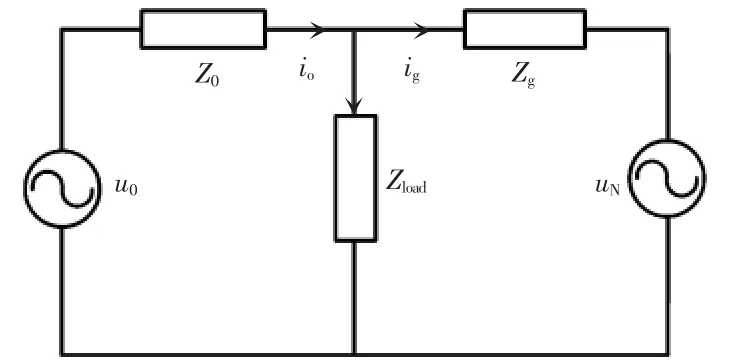
图3 系统并网模式简化框图Fig.3 Simplified diagram of system in grid-connected mode

本文研究了一种基于主从控制的间接电流控制策略。该控制策略在并网和离网工作时，从控制器一直采用PQ控制；与传统主从控制不同的是，为避免模式切换时控制结构的切换，主控制器在并网和孤岛两种模式下都按照电压源型方式运行，即在并网和孤岛时均采用电压电流双环控制。在离网模式时，主源逆变器采用传统的V/f控制，电容电压给定为恒定值；在并网时，通过控制电容电压来调节并网电流的大小，即调节并网功率。该控制方法避免了模式切换时控制结构的变化，能够实现逆变器输出电压的平滑切换，从而保证了本地负载的不间断供电，同时也减少了对电网的暂态冲击。

如图4所示为并网时电网电压vg、逆变器输出电压vc、并网电流ig的相量关系，其中vLg为电感Lg上的压降。由图可得

由式（8）可知，通过调节vc的幅值和相位，可以间接调节并网电流ig的大小，从而实现控制并网功率的目的。

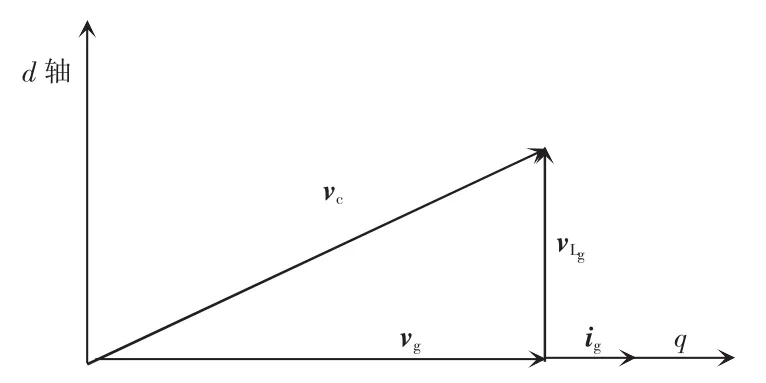
图4 并网时各电压电流相量关系Fig.4 Phasor diagram of voltage and current in gridconnected mode

2 基于比例积分谐振的控制策略

基于上述分析，整体的系统控制策略框图，如图5所示。图中：主电路采用三相全桥结构，Vdc是直流输入源；输出采用LC滤波器，Lf为滤波电感，Rf为电感寄生电阻，Cf为滤波电容；RL为本地负载，逆变器通过电感Lg与电网相连，PCC为并网开关，Si为模式切换开关，切换至状态1是并网模式，状态2为离网模式，ug为大电网电压，iLd、iLq分别为逆变器侧电感电流iL转换至dq坐标系下的电流反馈，vod、voq分别为逆变器输出电压vc转换至dq坐标系下的电压反馈，igd、igq为网侧电流ig转换至dq坐标系下的电流反馈值。

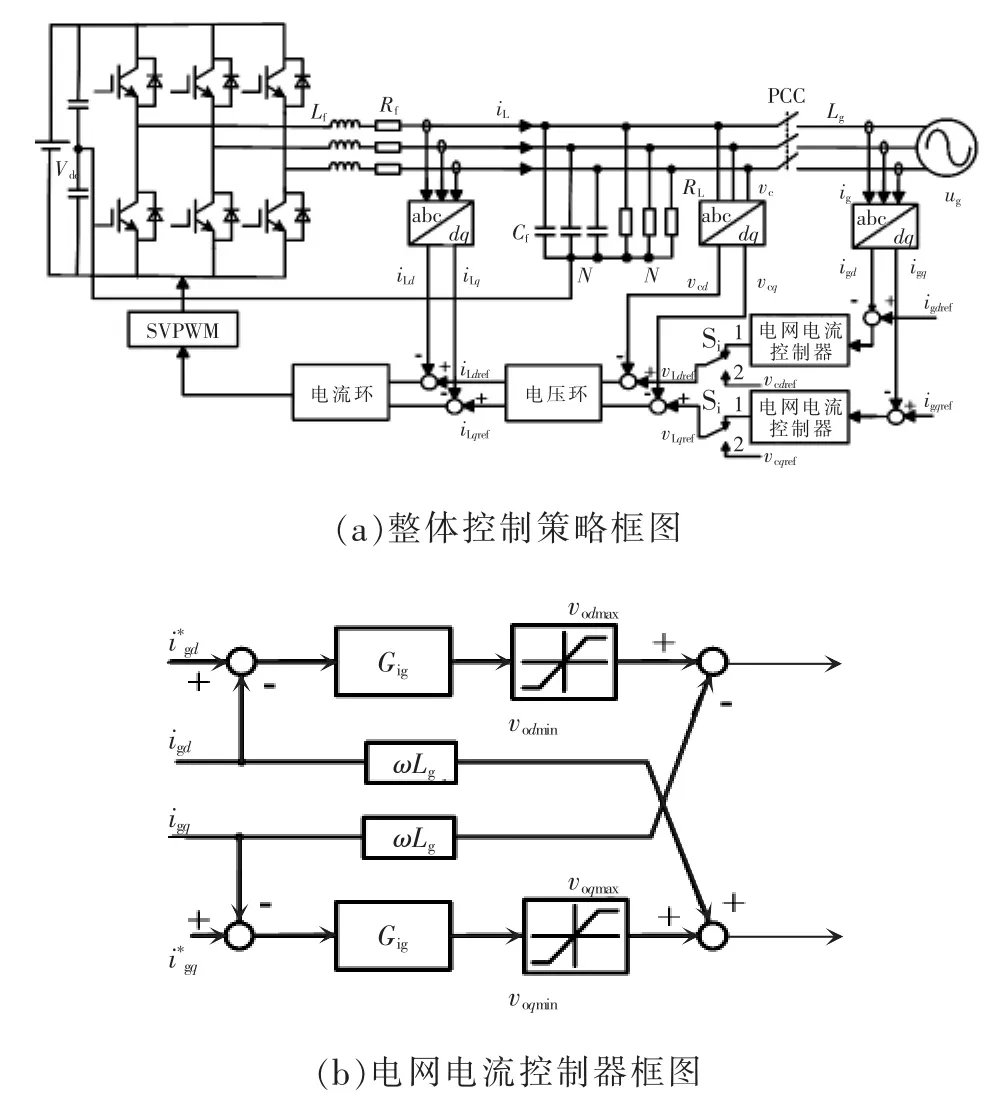
图5 基于间接电流控制的整体控制策略Fig.5 Overall control strategy based on indirect current control

针对离网模式下带不平衡负载工作的情况，由上文的分析可知，要想有效地抑制负载不平衡带来的输出电压不平衡问题，必须要对零序分量和负序分量进行控制。抑制系统负序分量和零序分量的控制框图如图6所示，图中上半部分为负序分量控制框图，下半部分为零序分量控制框图。

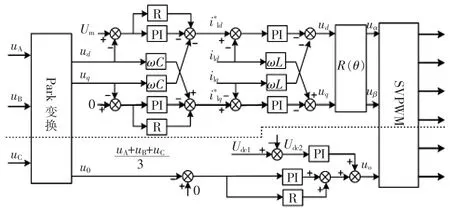
图6 负序分量和零序分量控制框图Fig.6 Control block diagram of negative-and zerosequence

由前面分析可知，Udc1-Udc2为直流量，而 （UA+UB+UC）/3为叠加一定直流偏置的、频率为50 Hz的交流量，所以选择谐振频率为50 Hz的比例谐振控制器进行抑制，且单比例控制器调节可以一定程度上抑制对直流偏置的放大作用。选择的准谐振控制器数学模型为

准谐振控制器的设计目标有以下3个参数：kr、ωc和 ω0，ω0为谐振频率。分别就 kr和 ωc两个控制参数对控制器产生的影响做进一步分析。不同kr和ωc时谐振控制器的波特图如图7所示。

图7（a）是当 ωc=1、kr变化时谐振控制器的波特图，可见，当kr从1增加到100，谐振控制器的幅值增益随着kr的变大而增加，相角保持不变。

图7（b）是当 kr=1、不同 ωc时谐振控制器的波特图，可见，当ωc从1增加到100时，随着ωc的增加，谐振点处的幅值增益减小，同时其相频特性的斜率越来越低，带来的谐振现象越不明显，但是对于谐振点外的频率，其增益越来越大。因此，需要选取合适的kr和ωc参数。

令s=jω，可得谐振控制器带宽为

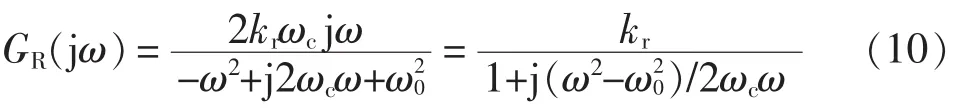
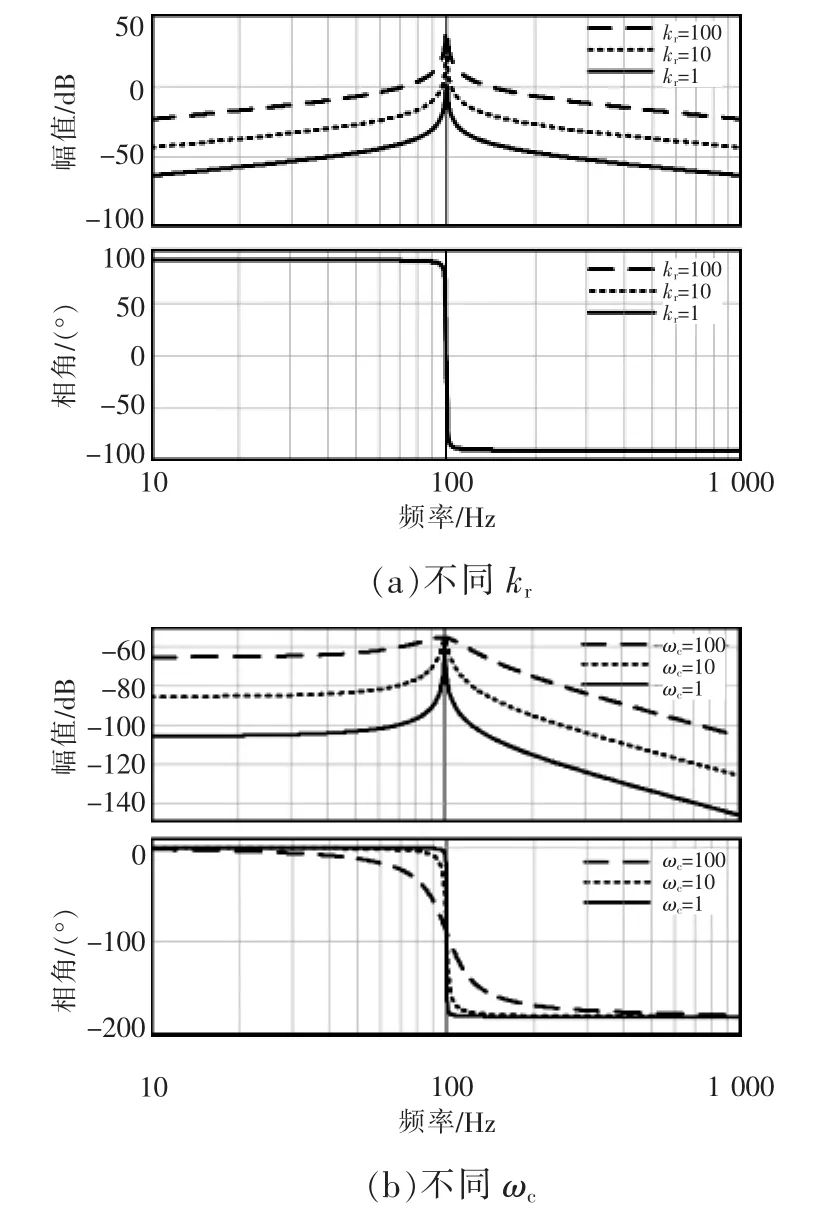
图7 不同kr和ωc时谐振控制器的波特图Fig.7 Bode diagram of resonance controller with different values krand ωc

GR（jω）的带宽为 ωc/π。离网运行时，逆变器频率为 50 Hz，令其变化范围为±0.5 Hz，则 ωc/π=1 Hz，即 ωc=π rad/s。

由图6可以得到电压环的开环传递函数为

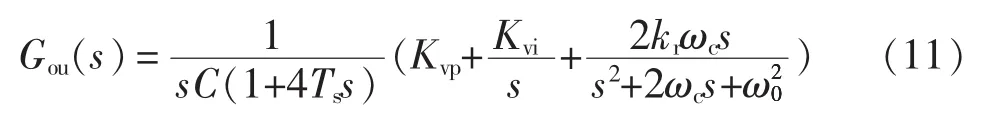
式中，Ts为系统的开关周期。依据典型Ⅱ型系统进行电压环路参数设计，可得

对于三相逆变器带不平衡负载工作，为了满足三相不平衡度在5%以内的要求，准谐振环节中带宽之内幅值增益应该大于26 dB，取边界条件为

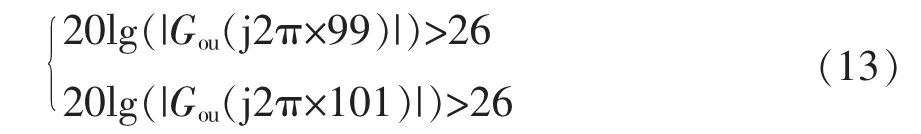
当kr2=0.8、ωc2=2π rad/s时，系统电压环传递函数波特图如图8所示。从图8中可以看到，系统的穿越频率为250 Hz，相角裕度为40°。满足设计要求。

列出电压环闭环传递函数为

为了验证加入准谐振控制器后系统在正序同步旋转坐标系下对2倍频负序分量的跟踪性能，给出电压环闭环波特，如图9所示，可见，在100 Hz处，系统幅值增益为0.023 dB，相角差为-1.021°，可以较好地抑制不平衡带来的负序2倍基波频率的分量。

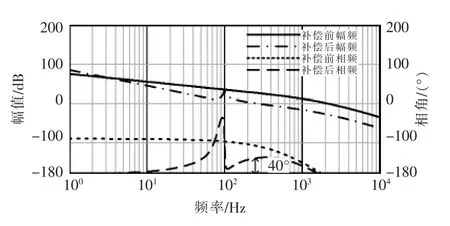
图8 PIR控制电压开环波特图Fig.8 Voltage open-loop bode diagram of PIR control

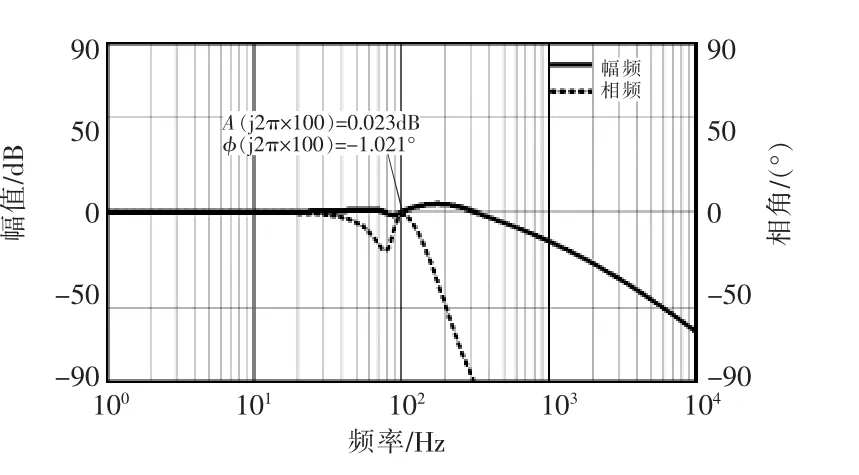
图9 PIR控制电压闭环波特图Fig.9 Voltage closed-loop bode diagram of PIR control

3 仿真验证

为了验证系统控制策略应用于三相不平衡负载的可行性及动态性能，本文在Matlab环境下搭建逆变器系统模型进行仿真分析，结果如图10～图12所示。

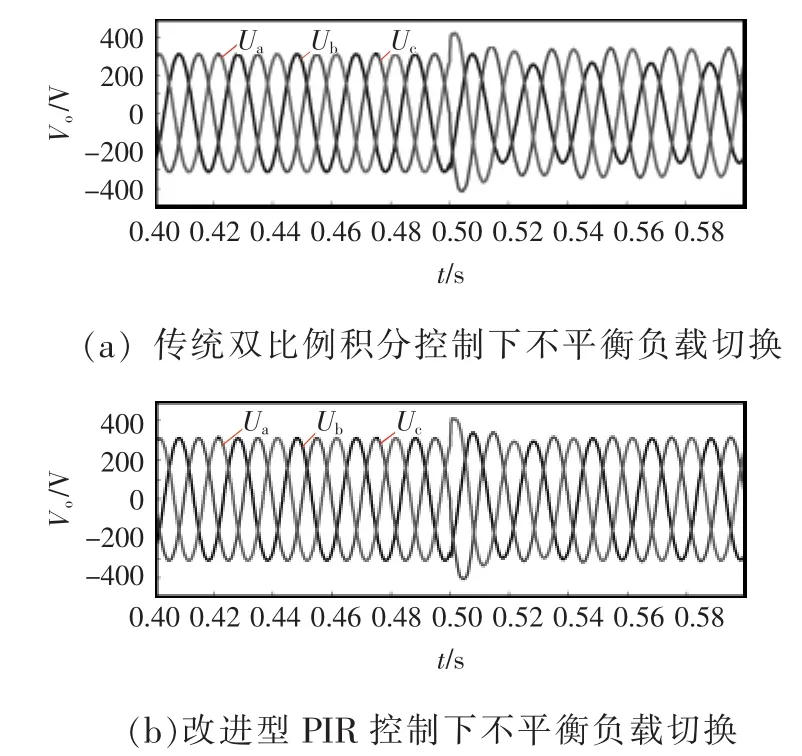
图10 两种不同控制策略的时域仿真波形对比Fig.10 Comparison of simulation waveforms in time domain between two different control strategies

图10（a）为传统电压电流双比例积分控制下的三相负载不对称仿真波形，电压电流环采用PI调节，不对零序分量进行分离控制，在0.5 s处本地负载从三相15 kW切换到单相 5 kW。由图可以看出，切载后三相输出电压不平衡度较差。把基于PIR的新型控制策略应用于逆变器系统中，在同样仿真条件下得到的仿真波形如图10（b）所示，可以看出，系统输出电压的不平衡度得到很大的改善，验证了前文分析的正确性以及控制方法的可行性。

针对控制策略的说明给出了如图11所示的两种不同控制策略dq轴分量对比，由图可知改进型PIR控制能较好地控制对2倍基频的负序分量进行抑制。

针对间接电流控制的切换策略，在满载状态下进行离网和并网之间切换的仿真，得到的波形如图12所示，图中，ig和iL分别为电网侧电流和逆变器侧电流，U为逆变器输出电压。由图可以看出无论是离网转并网还是并网转离网的状态下都能保持逆变器电压和并网电流的平滑无冲击切换，保证了切换过程中频率的稳定。

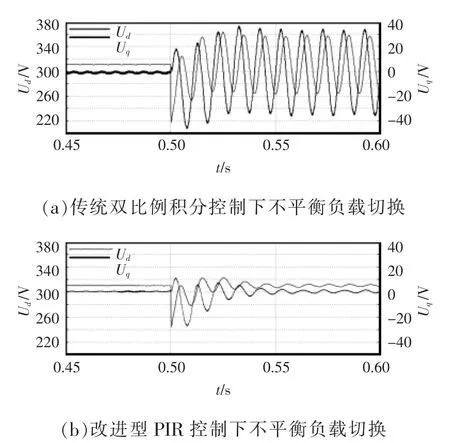
图11 两种不同控制策略dq轴分量对比Fig.11 Comparison of dq axis components between two different control strategies

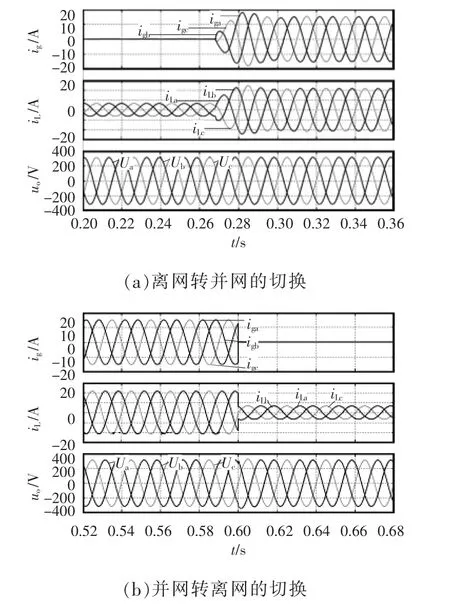
图12 应用间接电流控制策略的切换仿真结果Fig.12 Simulation results of switching under indirect current control strategy

4 实验结果

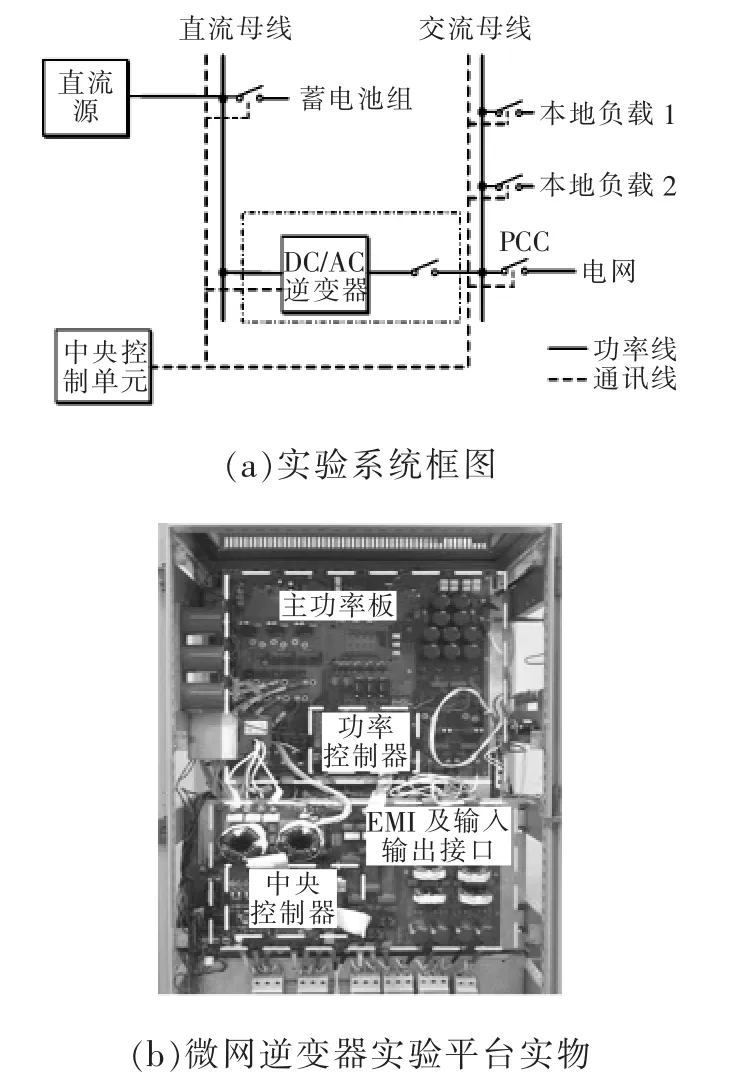
图13 微网逆变器实验平台Fig.13 Experimental platform of micro-grid inverter

表1 实验系统参数Tab.1 Parameters of experimental system

为了验证前文设计的抑制负载不平衡方法和中点电位控制的算法在实际应用中的有效性，搭建如图13所示的微网逆变器实验平台，实验系统参数如表1所示。光伏电池用Chroma公司的可编程直流源模拟，储能电池采用欧利特LCPC21-12胶体电池；三相桥臂采用MITSUBISHI公司的PM100CL 1A120IPM模块；电流采样用VAC公司的4646-X410板上LEM；控制方式为数字控制，采用TI公司的TMS320F28335 DSP芯片作为功率控制器。

为了验证上述方案的有效性，在实验中取最极端的单相负载工作，并且和传统双PI调节方案进行对比，结果如图14所示。采用传统双比例积分调节控制方法可以得到的实验波形如图14（a）所示，可以看到在单相4 kW负载工作状态下，波形的正弦度较差，不能保证三相输出电压平衡。同样的工作状态下，采用本文提出的对负序分量和零轴分量进行PIR调节方案，在单相5 kW负载条件下实验，得到的稳态工作波形如图14（b）所示。图14（c）是均压控制后的电容中点电位和中线电流的波形，电容电压能稳定在直流母线电压的一半，即360 V。由以上的实验结果可以看出，相较于传统方案，改进后的对负序分量和零序电压进行PIR控制方案在解决负载不平衡问题上切实有效，满足应用分裂电容的微网逆变器带不平衡负载工作的要求。

图14 两种不同控制策略的实验结果Fig.14 Experimental results under two different control strategies

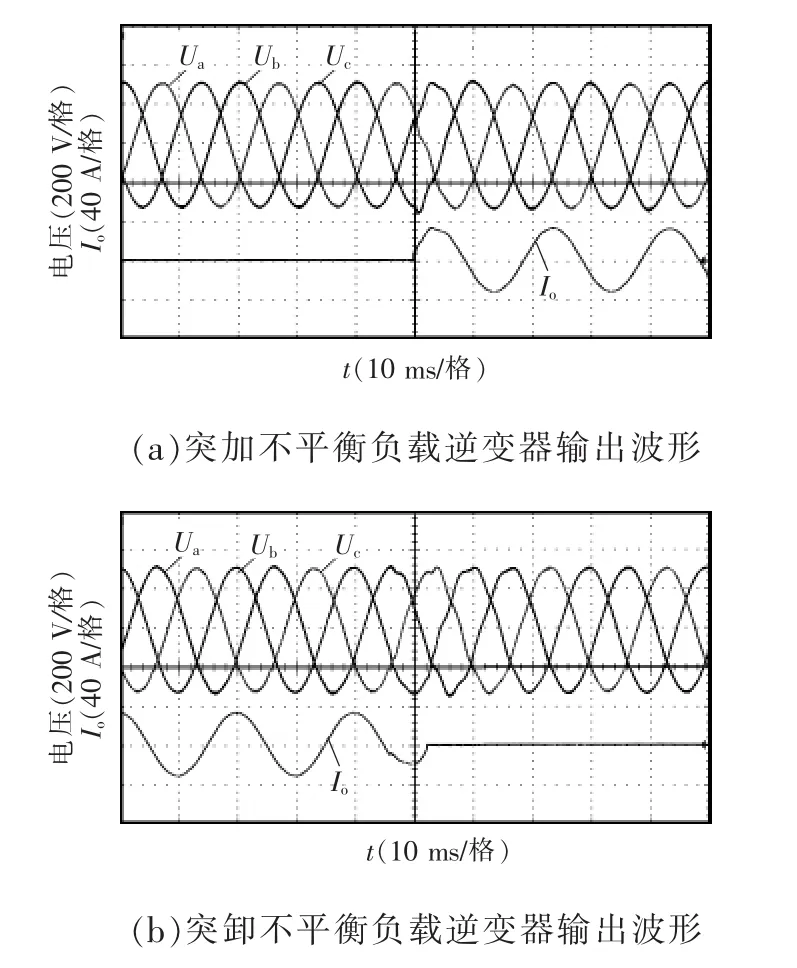
图15 突加突卸不平衡负载逆变器输出波形Fig.15 Dynamic experiment results of unbalanced loads

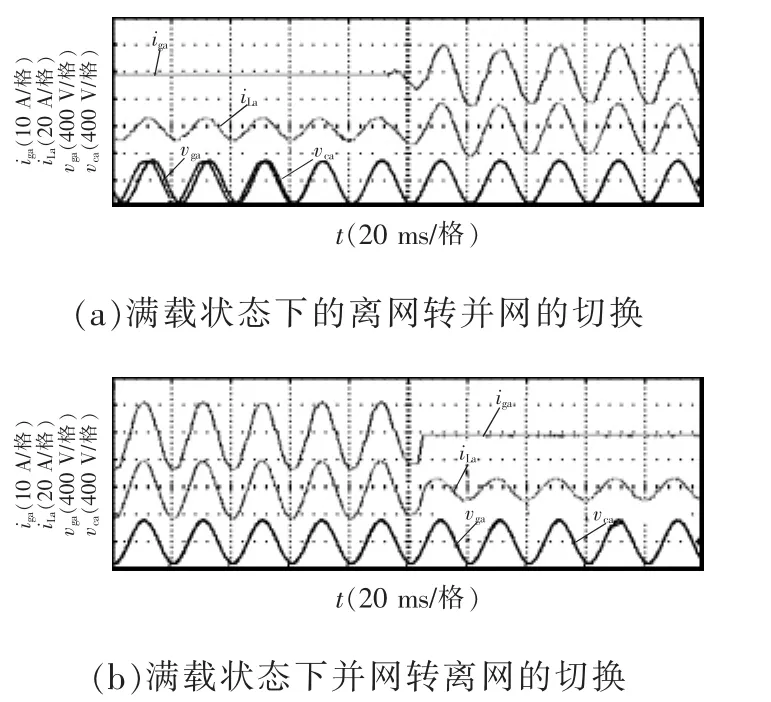
图16 应用间接电流控制策略的切换实验结果Fig.16 Experiment results of indirect current control strategy

为了验证逆变器带不平衡负载的动态性能，需要进行突加、突卸不平衡负载实验，实验结果如图15所示。图15（a）的实验条件为逆变器空载启动，稳定工作后突加单相5 kW负载；图15（b）为对应地突卸单相不平衡负载时逆变器输出电压与中线电流波形。由实验结果，加载和切载瞬间输出电压出现小幅波动，在几个周期内迅速完成调节，到达平衡。通过突加负载和突卸负载的不平衡负载实验，验证了在该控制方法下逆变器有较好的带不平衡负载运行动态性能。

针对间接电流控制策略，进行满载状态下离网模式和并网模式的切换实验，得到如图16所示的实验波形。可以看出，在两个模式切换过程中，电压与电流波形均平滑无冲击，验证了该切换方案的有效性。

5 结语

针对微网逆变器离网模式下带不平衡负载运行问题，本文应用分裂电容的逆变器拓扑，首先进行了原理分析，给出相关数学模型，将不平衡控制归结为控制其零序和负序分量两个角度，对不平衡输出电压进行正负序分离，并应用PIR控制进行准谐振控制；针对零序分量采用空间SVM的调制方式，同时针对微网逆变器传统切换策略中存在的缺陷提出了一种基于间接电流控制的整体控制策略。在理论分析的基础上，本文搭建了Matlab仿真模型，通过仿真验证了控制方案的正确性。最后在微网逆变器的实验平台上进行实验验证，证明了该复合控制方案可以保证微网逆变器在离网模式下带不平衡负载正常工作，并能在离网模式和并网模式之间实现平滑切换。

参考文献：

[1]王成山,王守相.分布式发电供能系统若干问题研究[J].电力系统自动化,2008,32（20）:1-4.Wang Chengshan,Wang Shouzu.Study on some key problems related to distributed generation systems[J].Automation of Electric Power Systems,2008,32（20）:1-4（in Chinese）.

[2]Rocabert J,Luna A,Blaabjerg F,et al.Control of power converters in AC microgrids[J].IEEE Transactions on Power Electronics,2012,27（11）:4734-4749.

[3]Blaabjerg F,Ma K,Zhou D.Power electronics and reliability in renewable energy systems[C]//IEEE International Symposium on Industrial Electronics.Hangzhou,China,2012:9-30.

[4]许津铭,谢少军,张斌锋.分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J].中国电机工程学报,2015,35（16）:4153-4166.Xu Jinming,Xie Shaojun,Zhang Binfeng.Overview of current control techniques for grid-connected inverters with LCL filters in distributed power generation systems[J].Proceedings of the CSEE,2015,35（16）:4153-4166（in Chinese）.

[5]徐怡.光储一体化微电网主逆变器控制策略研究[D].南京:南京航空航天大学,2015.Xu Yi.Research on the coordination control strategy of the master inverter applied in integrated photovoltaic and energy-storage micro-grid[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2015（in Chinese）.

[6]张兴,张崇巍.PWM整流器及其控制[M].北京:机械工业出版社,2012.

[7]Moran L,Ziogas P D,Joos G.Design aspects of synchronous PWM rectifier-inverter systems under unbalanced input voltage conditions[J].IEEE Transactions on Industry Applications,1992,28（6）:1286-1293.

[8]Kim J K,Lee J H,Jeong H G,et al.Improvement of gridconnected inverter systems with PR controllers under the unbalanced and distorted grid voltage[C]//proceeding of the 7th International Power Electronics and Motion Control Conference.Harbin,China 2012,2:1183-1187.

[9]Bottrell N,Prodanovic M,Green T C.Dynamic.Stability of a microgrid with an active load[J].IEEE Transactions on Power Electronics,2013,28（11）:5107-5119.

[10]Wang Xiongfei,Blaabjerg F,Loh P C.An impedancebased stability analysis method for paralleled voltage source converters[C]//2014 International Power Electronics Conference（IPEC-Hiroshima 2014-ECCE-ASIA）.Hiro-shima,Japan,2014:1529-1535.

[11]施婕,郑漳华,艾芊.直流微电网建模与稳定性分析[J].电力自动化设备,2010,30（2）:86-90.Shi Jie,Zheng Zhanghua,Ai Qian.Modeling of DC microgrid and stability analysis[J].Electric Power Automation Equipment,2010,30（2）:86-90（in Chinese）.

[12]黄如海,谢少军.基于比例谐振调节器的逆变器双环控制策略研究[J].电工技术学报,2012,27（2）:77-81.Huang Ruhai,Xie Shaojun.Double-loop digital control strategy based on proportional-resonant controller[J].Transactions of China Electrotechnical Society,2012,27 （2）:77-81（in Chinese）.

[13]Yepes A G,Freijedo F D,Doval-Gandoy J,et al.Effects of discretization methods on the performance of resonant controllers[J].IEEE Transactions on Power Electronics,2010,25（7）:1692-1712.

[14]刘京斗,张冀川,李会南.一种T型NPC三电平三相四桥臂中点电位控制策略[J].电源学报,2016,14（1）:68-73.Liu Jingdou,Zhang Jichuan,Li Huinan.A novel strategy of neutral point potential balancing for T-NPC three-level three-phase four-leg inverters[J].Journal of Power Supply,2016,14（1）:68-73（in Chinese）.

[15]韩莹,陈维荣,李奇,等.分布式电源并网逆变器谐波抑制方法[J].电力系统及其自动化学报,2014,26（9）:1-6.Han Ying,Chen Weirong,Li Qi,et al.Harmonic suppression methods for grid-connected inverter of distributed generation[J].Proceedings of the CSU-EPSA,2014,26（9）:1-6（in Chinese）.