轴向磁通磁场调制型电机的解析分析
2018-04-12宋志翌
宋志翌,黄 建,王 贯
(北京自动化控制设备研究所,北京100074)
0 引言
轴向磁通磁性齿轮是一种基于磁场调制原理的传动机构,它由极对数较少的高速永磁转子、调制环和极对数较多的低速永磁转子组成[1]。相比于机械齿轮,轴向磁通磁性齿轮在传动过程中无机械接触,具有传动效率高、可靠性高、过载保护能力强、无需定时润滑维护的优点[2-3]。轴向磁通磁场调制型电机采用定子电枢磁场代替轴向磁通磁性齿轮的高速永磁磁场,将存在双转子的轴向磁通磁性齿轮简化为只存在一个低速永磁转子的电机,大大降低样机加工装配的复杂度,在风力发电和电动汽车等低速大转矩直驱场合具有潜在的应用前景[4-7]。相比于径向拓扑结构,轴向拓扑结构可以更好地利用轴向空间,在转矩密度上具有优势[8-9]。
轴向磁通磁场调制型电机的磁密为三维分布,存在两种方法可用于计算轴向磁通磁场调制型电机的气隙磁场分布:三维有限元仿真法和解析分析方法。三维有限元仿真可建立电机的实际模型且考虑铁心的磁饱效应,仿真结果具有较高的精度,但是三维有限元仿真耗时长且对计算机的性能有较高的要求,这降低了电机设计优化的灵活度。解析分析方法取平均半径处的二维简化模型代替实际电机三维模型,且不考虑铁心的饱和效应,在保证计算精度的前提下可有效缩短计算时间[10-12]。
本文提出了一种计算轴向磁通磁场调制型电机气隙磁场和电机特性的简化二维解析分析方法。通过拉普拉斯方程或泊松方程并结合边界条件,求解出每个子域的矢量磁位,进而得到气隙磁场分布、空载反电势、电磁转矩和轴向磁拉力的解析表达式。为了评估解析方法的计算精度,对二维解析分析结果和三维有限元仿真结果进行了比较。
1 简化的二维解析模型
轴向磁通磁场调制型电机由定子、调制环和永磁转子这3个部件组成,其中调制环由导磁块与非导磁块交替排列而成,如图1所示。不同于常规的永磁同步电机,轴向磁通磁场调制型电机定子与永磁转子间存在调制环,不仅影响气隙磁场分布,同时使得轴向磁通磁场调制型电机电机特性的计算更加复杂。因此,提出了基于定子电枢绕组等效面电流法的二维解析分析方法。
将轴向磁通磁场调制型电机沿平均半径处展开并忽略定子开槽影响和铁心饱和效应,可得到电机的二维解析模型,如图2所示。由图2可见,二维解析模型可以分为4个区域:永磁体区域(I)、内层气隙区域(II)、外层气隙区域(III)和非导磁块区域(i)。其中,z1、(z2-z1)、(z3-z2)和(z4-z3)分别为永磁体厚度、内层气隙长度、导磁块厚度和外层气隙的长度。Β为非导磁块所占的跨距角,Q是导磁块的个数。Rm为电机的平均半径,b0为定子槽口宽度,S是定子槽数。
2 气隙磁场分布和电机特性的解析分析
2.1 各区域的矢量磁位方程及边界条件
在区域i中,矢量磁位Ai满足拉普拉斯方程:
(1)
式中,θi为第i个非导磁块的初始位置角。
由于导磁块的磁导率为无穷,所以第i个非导磁块与导磁块交界面磁场的切向分量为零。此外,第i个非导磁块与内、外层气隙交界面的矢量磁位是连续的。相应的边界条件可表示为:
(2)
Ai(θ,z2)=AII(θ,z2);Ai(θ,z3)=AIII(θ,z3)
(3)
式中,AII、AIII为内、外层气隙区域中的矢量磁位。
由矢量磁位方程式(1)和边界条件式(2)可得矢量磁位Ai的表达式为
(4)
(5)
(6)
(7)
(8)
在区域I中,矢量磁位AI满足泊松方程为
(9)
式中,Mz为永磁体的轴向磁化强度。
图3所示为Mz的分布图,由此可得Mz的表达式为
(10)
式中,Br为剩磁密度;pp为永磁体极对数;θp0为永磁转子的初始相位角。
由于永磁转子铁心的磁导率为无穷,所以永磁体与永磁转子铁心交界面磁场的切向分量为零。此外,永磁体与内层气隙交界面的矢量磁位是连续的。相应的边界条件可表示为:
(11)
AI(θ,z1)=AII(θ,z1)
(12)
由矢量磁位方程式(9)和边界条件式(11)可得矢量磁位AI的表达式为
AI(θ,z)=
(13)
式中:
(14)
(15)
在区域II中,矢量磁位AII满足拉普拉斯方程为
(16)
内层气隙与永磁体交界面磁场的切向分量相等,相应的边界条件可表示为
(17)
内层气隙与非导磁块交界面磁场的切向分量相等;由于导磁块的磁导率为无穷,内层气隙与导磁块交界面磁场的切向分量为零。相应的边界条件可表示为
(18)
由矢量磁位方程式(16)可得矢量磁位AII的表达式为
(19)
(20)
(21)
(22)
(23)
在区域III中,矢量磁位AIII满足拉普拉斯方程为
(24)
外层气隙与非导磁块交界面磁场的切向分量相等;由于导磁块的磁导率为无穷,外层气隙与导磁块交界面磁场的切向分量为零。相应的边界条件可表示为
(25)
由于该二维解析分析方法是基于定子电枢绕组等效面电流法的,因此可认为定子电枢绕组等效分布在外层气隙与定子轭交界处(z=z4),且每槽导体沿切向的分布宽度等于原槽口宽度b0。假设轴向磁通磁场调制型电机定子采用每极每相槽数为1的集中整矩绕组,则在外层气隙z=z4处,定子电枢绕组电流密度等效分布模型如图4所示。
定子电枢绕组等效电流密度的表达式为
(26)
式中,Im为相电流有效值;Nt为每槽导体数;θs0为第一槽内相电流的初始相位角;b0为槽口宽度。
由于定子轭的磁导率为无穷,且外层气隙与定子轭交界面存在等效面电流,因此边界条件式可表示为
(27)
由矢量磁位方程式(24)可得矢量磁位AIII的表达式为
(28)
(29)
(30)
(31)
(32)
2.2 气隙磁密分布
内层气隙磁密轴向分量BzII和切向分量BθII的表达式为式(33)、式(34);外层气隙磁密轴向分量BzIII和切向分量BθIII的表达式为式(35)、式(36)。
(33)
(34)
(35)
(36)
2.3 电机特性
可以通过对外层气隙磁密积分获得电机单相磁链,从而得到空载反电动势表达式为
(37)
由麦克斯韦应力张量法和牛顿第三定律可得电机的电磁转矩和轴向磁拉力表达式为:
(38)
(39)
Tm=-(Ts+Tp)
(40)
(41)
(42)
Fm=-(Fs+Fp)
(43)
式中,Tp、Ts、Tm为永磁转子、定子和调制环所受的电磁转矩;Fp、Fs、Fm为永磁转子、定子和调制环所受的轴向磁拉力。
3 解析分析与三维有限元仿真对比
为了评估解析分析的正确性,将解析结果与三维有限元仿真结果进行比较,电机结构参数如表1所示。
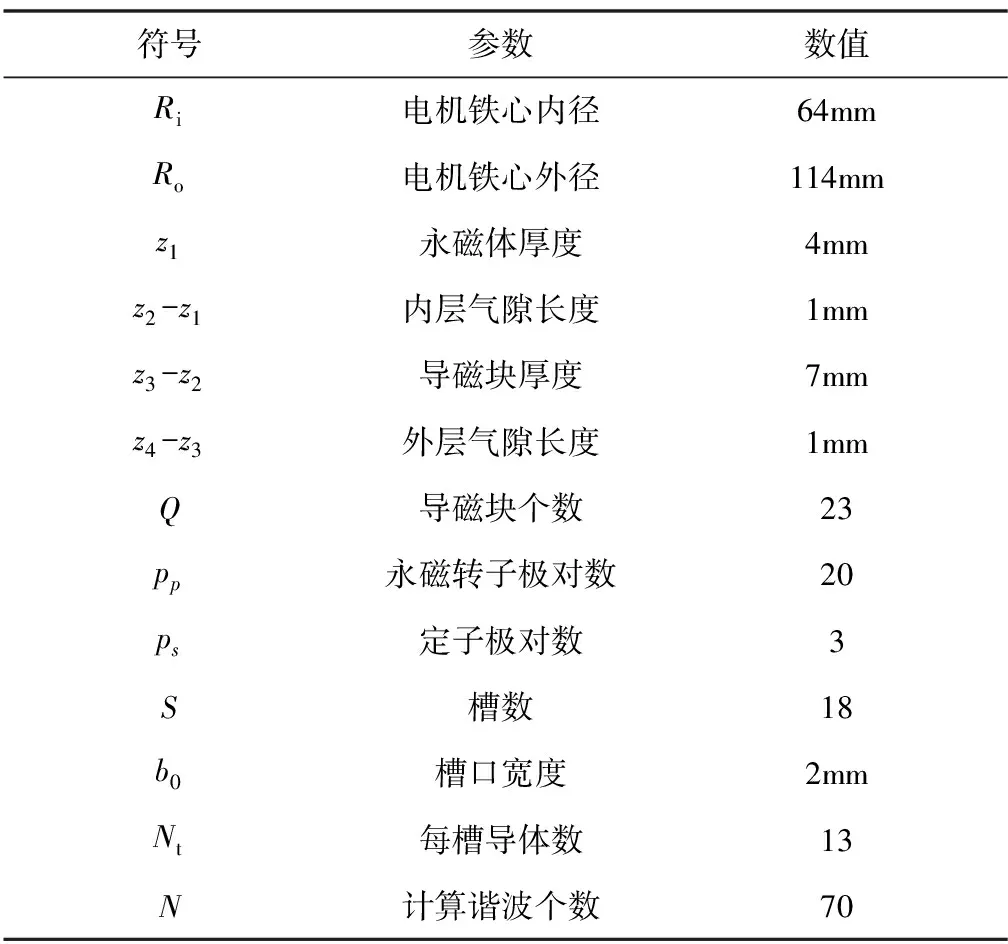
表1 轴向磁通磁场调制型电机结构参数
图5和图6所示分别为永磁体和三相定子电枢绕组单独作用时,内、外层气隙区域中的磁场分布波形。由图可见,由于导磁块的存在,气隙磁场的调制作用非常明显,解析计算结果与三维有限元仿真结果具有很好的一致性。
空载反电动势波形如图7所示。由图7可知,解析计算的空载反电势幅值比三维有限元仿真结果大了7.7%。
图8给出了不同相电流下的转矩特性。由图8可知,解析分析结果与三维有限元仿真结果具有较好的一致性。图9给出了导磁块的极弧比对电磁转矩的影响。由图9可知,解析分析计算的电磁转矩与三维有限元仿真结果的最大误差在10.3%以内,这主要由于解析计算没有考虑定子铁心、导磁块和永磁转子铁心的饱和作用。重要的是,解析计算与有限元仿真的曲线变化规律一致,并且永磁转子转矩的最大值均出现在导磁块极弧系数0.5处。
定子通三相对称的直流电,当永磁转子从0°旋转到18°(旋转一对极)时,永磁转子所受的轴向磁拉力如图10所示。由图10可知,解析分析计算的轴向磁拉力三维有限元仿真之间的误差在9.7%以内。
由图9和图10可知,解析计算结果和三维有限元仿真结果存在一定的差异。这主要是由于解析分析忽略定子开槽对气隙磁密的影响且假设软磁材料的磁导率为无穷,而三维有限元仿真建立电机的实际模型且考虑铁心的饱和效应。
为了研究解析分析中谐波个数的选择对计算结果的影响,图11给出了谐波个数对永磁转子转矩和计算时间的影响。由图11可知,当谐波个数大于等于70时,电磁转矩差值小于6.3%。这表明谐波个数选取70已经可以较为准确地预测电机的永磁转子转矩。此种选择下解析计算时间为74s,而三维有限元仿真时间最少需要30min。由于解析分析在大大缩短了计算时间的同时可以较为准确地预测气隙磁场分布和转矩随着参数的变化规律,因此适用于初始设计阶段电机参数的确定。
4 结论
本文提出了一种二维解析分析方法用于计算轴向通量磁场调制型电机的气隙磁场分布和电机特性。该方法考虑到调制环存在对气隙磁密的影响,分析结果表明解析分析方法可以较为准确地预测气隙磁场分布和转矩随着参数的变化规律。解析结果与三维有限元仿真结果具有很好的一致性,两者之间的误差在10.3%以内。由于解析分析在保证计算精度的前提下大大缩短了计算时间,且解决了三维有限元分析模型复杂的问题,因此该方法适用于轴向磁通磁场调制型电机初始设计阶段电机参数的确定,提高了电机优化设计的灵活性与高效性。
[1]Atallah K, Howe D. A novel high-performance magnetic gear[J]. IEEE Transactions on Magnetics, 2001, 37(4): 2844-2846.
[2]Atallah K, Calverley S D, Howe D. Design, analysis and realisation of a high-performance magnetic gear[J]. IEE Proceedings-Electric Power Applications, 2004, 151(2): 135-143.
[3]Mezani S, Atallah K, Howe D. A high-performance axial-field magnetic gear[J]. Journal of Applied Physics, 2006, 99(8): 2844.
[4]Brönn L. Design and performance evaluation of a magnetically geared axial-flux permanent magnet generator[D]. Stellenbosch: Stellenbosch University, 2012: 36-40.
[5]Johnson M, Gardner M C, Toliyat H A. Design and analysis of an axial flux magnetically geared generator[J]. IEEE Transactions on Industry Applications, 2017, 53(1): 97-105.
[6]Atallah K, Rens J, Mezani S, et al. A novel “Pseudo” direct-drive brushless permanent magnet machine[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4349-4352.
[7]Morimoto E, Hirata K, Niguchi N. Performance evaluation of an axial-type magnetic-geared motor[J]. Electrical Engineering in Japan, 2016, 194(1): 48-59.
[8]Cavagnino A, Lazzari M, Profumo F, et al. A comparison between the axial flux and the radial flux structures for PM synchronous motors[J]. IEEE Transactions on Industry Applications, 2002, 38(6): 1517-1524.
[9]Huang S, Aydin M, Lipo T A. A direct approach to electrical machine performance evaluation: Torque density assessment and sizing optimization[C]// International Conference on Electrical Machines. Bruge, 2002.
[10]Rahideh A, Korakianitis T. Analytical magnetic field calculation of slotted brushless permanent-magnet mach- ines with surface inset magnets[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2633-2649.
[11]Zhu Z Q, Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting[J]. IEEE Transactions on Magnetics, 1993, 29(1): 143-151.
[12]Lubin T, Mezani S, Rezzoug A. Development of a 2-D analytical model for the electromagnetic computation of axial-field magnetic gears[J]. IEEE Transactions on Magnetics, 2013, 49(11): 5507-5521.
