单轴旋转捷联惯导系统重力扰动补偿方法研究

常路宾，覃方君，查　峰

(1. 海军工程大学 导航工程教研室，武汉 430033； 2. 国防科技大学，长沙 410073)

0　引言

惯性导航具有自主性强、隐蔽性好、不受外界干扰等优点，在导航领域具有极强的生命力，在国防科技和军事应用领域有着不可替代的作用。就航海领域而言,舰用惯性导航系统是舰载导航系统中最为重要的导航系统，是我国海军“走得远”、“打得准”的信息保障。近年来，随着光学惯性器件以及旋转调制等系统补偿技术的发展和应用，我国惯性导航技术取得了突破性进展，尤其是旋转调制技术的发展和应用，使得我国光学捷联惯导系统精度得到大幅提升[1-5]。

随着惯导精度的不断提升，原先所忽略的一些误差源成为制约惯导精度进一步提升的关键，而重力扰动正是这类误差。重力扰动是由地球物理场所决定的，不受旋转调制等系统级补偿方法的影响。为了进一步提升惯导精度，必须补偿重力扰动或对其产生的系统误差进行抑制。国外典型惯性导航系统如Litton公司的LN-93E系统在其初始对准阶段以及惯导解算阶段分别考虑重力扰动的补偿，所需的重力扰动信息是由提前存储好的测量重力所提供[6]。除进行补偿消除其不利影响外，还可以通过阻尼的方式抑制重力扰动所引起的舒拉振荡误差，如Sperry公司的AN/WSN-7系统即采用了三阶阻尼的方式抑制重力扰动所引起的系统误差[7]。天津航海仪器研究所的翁海娜等也研究了常速度误差反馈阻尼和相位超前串联阻尼对重力扰动所引起的系统误差的抑制[8]。

近年来，随着高阶重力模型的发展，利用高阶重力模型计算重力扰动并进行补偿受到人们的广泛关注。典型的高阶重力模型由德国波尔茨坦GFZ研制的EIGEN-6C4和美国的国家地理信息情报局NGS研制的EGM2008[9-10]。北京航空航天大学、清华大学、国防科技大学以及西北工业大学等单位通过实测实验验证了基于高阶球谐模型计算重力扰动进而补偿对惯导精度的提升[9,11-13]。翁浚等通过误差分配理论指出当惯导精度优于0.2nm/h时，进行重力扰动补偿能够提升惯导精度[13]。显然，目前旋转调制捷联惯导系统已经优于0.2nm/h，因此有必要进行重力扰动补偿。基于上述背景，本文以单轴旋转调制捷联惯导系统为例，利用EIGEN-6C4计算惯导所在地重力扰动信息，研究重力扰动补偿对惯导精度的提升。

1　单轴旋转调制基本原理

旋转调制惯导系统的基座与载体固联，系统通过旋转机构为惯性测量单元(Inertial Measurement Unit, IMU)提供转动力矩，使IMU绕单轴或者多个相互正交的轴旋转。旋转调制惯导系统的陀螺和加速度计的输出在旋转坐标系内测得。将测试数据经旋转分解后转换到导航坐标系进行解算，其量测量增加了一次坐标变换。记旋转系为p、导航系为n、载体系为b、惯性系为i，旋转调制惯导系统的误差方程为

(1)

(2)

(3)

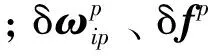
从式(2)中也可以看出，重力误差δg是不受旋转调制的影响的，因此必须加以补偿或抑制其引起的系统误差，否则会影响惯导定位精度。

式(2)直接反映了重力误差对惯导解算的影响，即产生速度误差，进而激励位置误差。重力误差对惯导系统精度的另一方面的影响在于初始对准阶段。将式(2)移项整理如下

(4)

令

(5)

式(4)中2个水平分量分别为

(6)

在Kalman滤波精对准中，速度观测量一般是已知的，其相应的微分也是已知的，因此式(5)所对应的观测是已知量。同时，在单轴旋转调制惯导系统中(一般绕天向轴旋转)，可近似认为水平加计零偏为零。进一步，加计输出的水平投影一般为小量。基于上述讨论，同时忽略二阶小量，根据式(6)可得到水平姿态角Kalman滤波精对准的稳态误差，即

(7)

上述正是垂线偏差的定义，也即对于绕天向轴单轴旋转的惯导系统，垂线偏差是其对准结果的主要误差源。

(8)

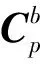
ω(t)=

(9)

2　基于高阶重力模型的重力扰动计算

地球上某点的重力位等于引力位和离心力位之和，即

W=V+Q

(10)

其中引力位和离心力位分别为：

(11)

(12)

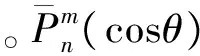
(13)

由于需要在导航坐标系(笛卡尔坐标系)下进行重力扰动补偿，因此需要将上述重力矢量投影到导航系下。球坐标系与地球坐标系之间的关系为

(14)

由该关系式即可得到地球坐标系下的重力矢量，记为

(15)

进而利用载体位置信息得到导航系内的重力矢量

(16)

其中

(17)

在求式(13)中的导数时，需要求解等阶次和非等阶次完全正常化缔合勒让德函数及其导数，具体求解过程参见文献[9, 13]。上述计算中所需的球谐参数由EIGEN-6C4所提供。

3　仿真实验

为了验证单轴旋转调制捷联惯导系统重力扰动补偿效果，设计相应的静基座仿真实验。仿真位置选取为海军工程大学所在地，经纬度分别为30.57579°和114.2424°。利用该位置作为输入(假定高度为0)，通过重力球谐模型求解重力扰动，阶次分别取EIGEN-6C4所对应的最高阶次，即2190。高阶重力矢量的2个水平分量如图2所示。图中横坐标表示球谐模型的阶次。

单轴正反转停的转动角速度如式(9)所示，其中ts=5s、T=140s、c=π/30。仿真中假定陀螺漂移为[0.01，0.01，0.003](°)/h，加速度计常值零偏为[100，100，50]μg，系统采样间隔为Ts=0.1s，仿真时间为72h。重力扰动补偿前后导航结果如图3～图5所示，其中图3所示为速度误差，图4所示为经纬度误差，图5所示为位置误差。从图中可以看出，经重力扰动补偿后，惯导精度有一定提升，尤其是在经度误差上。这是因为影响经度误差的因素主要在于东向重力扰动。从图2可以看出，东向重力扰动较大，因此其引起的位置误差也较大；经补偿后，精度提升也比较明显。

需要指出的是，为了更清晰地显示重力扰动对系统误差的影响，上述补偿的重力扰动信息是基于精确位置信息计算的。实际惯导自主导航重力扰动补偿中并不知道精确的位置信息，需要依据惯导解算位置计算相应的重力扰动，从而会引入一定的误差。但是随着惯导精度的进一步提升，位置误差所带来的重力扰动误差也会相应减少。今后的研究将重点针对实际应用场合，研究位置误差带来的重力扰动误差对系统精度的影响。

4　结论

本文以单轴旋转捷联惯导系统为例，研究了重力扰动补偿对系统精度的提升作用。文中指出随着惯导精度的不断提升，重力扰动将成为制约惯导自主定位导航精度进一步提升的关键。基于高阶重力球谐模型计算重力扰动信息，然后在惯导解算中进行相关补偿，可在一定程度上提升系统精度，仿真实验验证了重力扰动补偿对系统精度提升的效果。

[1]翁海娜，陆全聪，黄昆，等．旋转式光学陀螺捷联惯导系统的旋转方案设计[J]．中国惯性技术学报，2009,17(1)：8-14.

[2]龙兴武，于旭东，张鹏飞，等．激光陀螺单轴旋转惯性导航系统[J]．中国惯性技术学报，2010,18(2)：149-153.

[3]于旭东. 二频机抖激光陀螺单轴旋转惯性导航系统若干关键技术研究[D]. 长沙:国防科学技术大学, 2011.

[4]魏国. 二频机抖激光陀螺双轴旋转惯性导航系统若干关键技术研究[D]. 长沙:国防科学技术大学, 2013.

[5]孙伟强，曹东，戚嘉兴，等．旋转调制式惯导系统隔离载体运动算法[J]．中国惯性技术学报，2017,25(4)：432-435.

[6]George G．High accuracy performance capabilities of the military standard ring laser gyro inertial navigation unit [C]// IEEE Position Location and Navigation Symposium. IEEE, 1994: 464-473.

[7]Stamenkovich M, Carvil J．Application of the Digital Nautical Chart (DNC) database to help identify areas of vertical deflection in the Ring Laser Gyro Inertial Navigator (AN/WSN-7) [C]// IEEE Position Location and Navigation Symposium. IEEE, 2000: 299-303.

[8]翁海娜，李鹏飞，高峰，等．高精度惯导系统重力扰动的阻尼抑制方法[J]．中国惯性技术学报，2017,25(2)：141-145.

[9]铁俊波，吴美平，蔡劭琨，等．基于EGM2008重力场球谐模型的水平重力扰动计算方法[J]．中国惯性技术学报，2017,25(5)：624-629.

[10]Förste C, Bruinsma S L, Abrikosov O, et al．EIGEN-6C4 the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse [C]// 5thGOCE User Workshop. Paris, 2014.

[11]Wang J, Yang G, Li X, et al. Application of the spherical harmonic gravity model in high precision inertial navigation systems[J]. Measurement Science and Technology, 2016, 27(9): 095103.

[12]Wu R, Wu Q, Han F, et al. Gravity compensation using EGM2008 for high-precision long-term inertial navigation systems[J]. Sensors, 2016, 16(12): 2177.

[13]翁浚．机抖激光陀螺捷联惯导系统精度改善关键技术研究[D]. 西安：西北工业大学, 2017.