一种采用压电复合音叉的电流传感器研究
2018-04-11杨爱超周煦光张吉涛
王 英,杨爱超*,周煦光,刘 见,朱 亮,李 敏,吴 宇,张吉涛,何 伟
(1.国网江西省电力有限公司电力科学研究院,南昌 330096;2.郑州轻工业学院,郑州 450002;3.广西百色学院,广西 百色 100120)
电流测量技术对电力系统中各级输电线路和设备的保护、监测、控制、分析和决策及电能计量起着重要的作用。电流测量技术大致可以分为接触式电流测量和非接触式电流测量。典型的接触式电流测量器件有分流器和电磁感应式电流互感器,但是因测量时必须串联接入通路中而缺少与输电线路之间必要的电气隔离,容易对人身安全和二次设备造成伤害[1]。因此,非接触式测量越来越成为研究的热点。
电磁式电流非接触测量技术以罗氏线圈为代表。由于罗氏线圈的绕线均匀没有磁芯因此不存在磁芯饱和问题,并且具有较大的动态范围因此更适合用于大电流的测量,同时可以用于测量尺寸很大或形状不规则的导体电流。罗氏线圈在高压设备瞬态电流测量、50 Hz输电线电流测量和局部放电测量等方面都有卓越表现[2-3]。罗氏线圈在测量中会有一些缺陷:它的性能会受到外界温度、磁场等因素的影响,这是由于罗氏线圈是空心线圈没有高磁导率材料作为磁芯进行聚磁,更容易受到外界磁场的干扰;另外,穿心导线中心位置的变化对输出信号影响极大。
霍尔效应式电流非接触测量技术的核心为霍尔元件。霍尔元件被广泛地应用在磁场测量、微位移感知、压力、振动和加速度等非电量的测量,也可对由电流产生的环形磁场进行探测[4]。作为非接触式电流测量方法的一种,霍尔式电流测量装置是将霍尔元件放入到开口的软磁磁芯以达到电流探测的目的,是一种新型的复合式传感器。霍尔式电流传感器因开口气隙的存在影响了整个磁路磁通汇聚的效率,但是在一定程度上输出信号避免了由高磁导率磁芯的饱和失真[5]。霍尔式的电流传感器最显著的特点是具有很大的响应带宽,但是霍尔元件毕竟是一个有源器件,在使用过程中必须要外加偏置电压以保证它的正常工作,限制了其适用范围[6]。
光电式电流非接触测量技术是针对电力系统用传统电磁感应式电流互感器具有磁饱和、铁磁谐振、动态范围小,频带窄以及绝缘麻烦等缺点,利用光学传感器技术发展起来的一种测量技术,其核心器件—光电式电流互感器OCT(Optical Current Transformer)可以克服上诉缺点且具有良好的电气绝缘特性,并成为近年来研究的热点[7]。光波在光学介质(例如光纤、光学晶体等)中的传播可用光强,频率、波长、相位和偏振态来描述,当其中某一参数随外界因素发生变化时,可调制该参数作为敏感量去测量使其改变的参数值,最常用的调制方法是基于法拉第效应的偏振角调制。根据核心传感元件的不同,该类传感器又可以分为磁光材料和全光纤型电流传感器。随着上世纪六十年代光纤的发明,光纤电流传感器的高绝缘性和强抗电磁干扰性等优良性能,光纤传感技术迅速发展并逐渐应用于高电压线路传输及微弱电流的探测。但是光电式电流传感器的光源稳定性直接影响测量性能,并且易受环境振动、温度变化的影响因而导致不良的稳定性;另外复杂的光路也限制了其广泛应用。
巨磁阻/阻抗式电流非接触测量技术利用巨磁阻效应或者巨磁阻抗效应进行测量。巨磁阻效应GMR(Giant Magnetoresistance),是指磁性材料的电阻率在有外磁场作用时较之无外磁场作用时存在巨大变化的现象[8]。美国北卡罗来纳大学Dogaru等人设计了用于非磁性金属表面缺陷检测的巨磁阻漏电流传感器,由于该传感器具有自校准的性质使得后端的调理电路更简单,可以在220 mV/mA的灵敏度下测量从直流到1 MHz的电流频率[9]。但是,由于固有1/f噪声的存在使得基于GMR效应的电流传感器件在低频时测量能力较弱。巨磁阻抗效应是指铁磁材料的交流阻抗会随外加磁场而发生显著变化[10]。GMI效应的存在极其依赖材料的特性,研究发现非晶和纳米晶类磁性带材、丝材及薄膜中都发现了GMI效应,这些发现为电流传感器的研发提供了更多的材料选择。2003年,韩国忠南国立大学Rheem等人采用基于钴基非晶带材Co66Fe4 B15Si15设计了一种巨磁阻抗效应电流传感器。传感器的输出电压与输入电流具有良好的线性关系,且该传感器测量直流磁场的性能好于测量交流磁场[11]。但是,基于巨磁阻/阻抗式效应的电流测量技术依然需要稳定的电源供电以保证测量的持续性和稳定性。
压电式电流非接触测量技术利用压电效应原理进行测量[12]。2006年美国加州大学伯克利分校Wright P K课题组最早提出复合悬臂梁式电流传感器的原始模型[12],该器件由压电双晶片悬臂梁弹性结构和NdFeB块状永磁体组成,用于家用电器中60 Hz双芯电线中的电流监测。根据安培左手定则在静态磁场中的通电电流会产生安培力,带永磁体的悬臂梁结构会受到纵向安培力的反作用力,因此当有交变电流输入悬臂梁结构会带动贴在夹持端的压电材料产生同样频率的机械振动。它的固有谐振频率为110 Hz,NdFeB永磁体被放置于梁的末端目的是进行频率调谐和提供静态偏置磁场。2009年,一种用于电流测量的悬臂梁结构的MEMS器件模型被提出[13],AlN作为悬臂梁并提供输出。将其在型号为16 AWG 和18 AWG的双芯电缆上进行测试,给定20 A和13 A的输入电流,输出的灵敏度分别达到0.87 mV/A和1.08 mV/A。日本茨城大学微系统实验室的Isagawa等人采用与伯克利课题组提出结构类似的MEMS级电流传感器件,不同的是该器件使用了5片并行排列的PZT串联起来作为输出,并测量了该器件在通有直流电流的单芯和双芯电缆激励下的电流灵敏度。同时将该器件用于带开关的直流电流通路中用于检测开关关断时的脉冲信号,测试结果表明对双芯线路中直流电流测量的最高灵敏度可以达到7 mV/A[14]。当前已有的复合悬臂梁式电流传感器模型虽然相对其他原理的测量技术[15]具有较高的灵敏度,但是灵敏度依然不够高,特别是针对弱电流的测量[16]。这是因为其弹性结构悬臂梁的机械品质因数(Q值)依然不够高导致压电转换过程中的损耗依然不小。
1 工作原理及结构
为了提高低频微弱电流的测量灵敏度,针对本文研制了一种采用压电复合音叉的电流传感器(或压电复合音叉式电流传感器)来进行非接触测量,结构如图1(b)所示,其由一个弹性铜音叉、两块压电片和一组永磁铁组成。当传感器处于载流电线(Ii)周围交变磁场(Hac)中时,永磁体在交变磁场Hac作用下因磁扭矩效应产生扭矩并驱动音叉臂及压电片产生形变;因压电效应,形变的压电片两端电极之间输出交变电压信号,从而实现电流的测量。由于两音叉臂振动时存在谐振耦合作用,因此该传感器相比已有的单悬臂梁结构(图1(a))具有更强的振动和更高的谐振Q值,从而产生更高的电压输出和灵敏度。
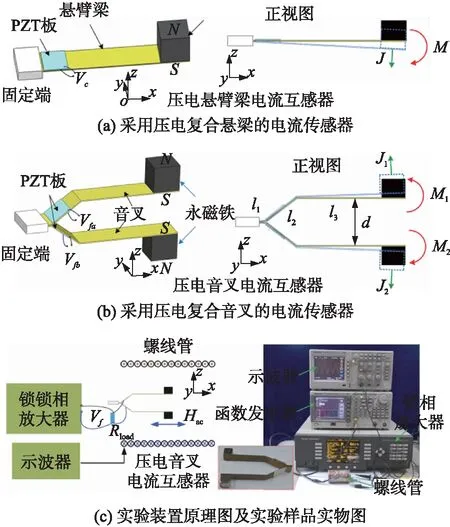
图1 (a);(b);(c)
如图1(b)所示,根据安培定律,当载流导线流经交变电流Ii时,将在其周围(空气)产生交变磁场Hac,其以电线中心为圆心呈环形分布,大小为Hac=Ii/2πr,其中为Ii电流大小,r表示距离电流中心的距离。现将压电复合音叉式电流传感器置于电线附近,并且两音叉臂关于电线对称。此时,由于音叉臂自由端的永磁铁的极化磁场(J1、J2)与电线磁场Hac发生磁场交互作用,两个永磁铁将产生相反的弯曲扭矩[M1、M2,M1(M2)=J1(J2)·VM×Hac,其中VM为永磁铁的体积],同时导致两音叉臂发生反相振动。当音叉工作在基本谐振模态时,其固定端相当于一个无振动的节点。因此,弹性波能够以从一个音叉臂自由端传播到另一边而损失很少的能量。此外,因为音叉工作在半波谐振模态,所以该弹性波到达另一音叉臂自由端时将发生180°的反相,其刚好与该音叉臂自由端处振动发生同相叠加。因而,每个音叉臂具有增强的振动和提高的Q值。为了更好地研究由音叉臂之间谐振耦合效应导致的振动增强机制,本文利用有限元法软件COMSOL MULTIPHYSICS的Structural Mechanics Module模块计算了相同激励下单悬臂梁和音叉的谐振态位移和应力分布,如图2所示。为了简化有限元计算,将磁扭矩产生的机械力沿z轴方向直接施加在悬臂梁及音叉臂的自由端。计算过程中,先在固定端施加xyz三轴零位移,并利用本征模态计算功能确定结构的主谐振态;再在结构自由端施加以主振频率为信号频率的机械力,最后计算得到主谐振态下的位移及应力分布。由图2可知,在主谐振态下,每个音叉臂的最大振动位移约为悬臂梁自由端的3.5倍,而其固定端附近平均应力则为悬臂梁相应位置的4倍。为了获得最大化的电压输出,应将压电片放置在应力最大处,即音叉固定端附近。
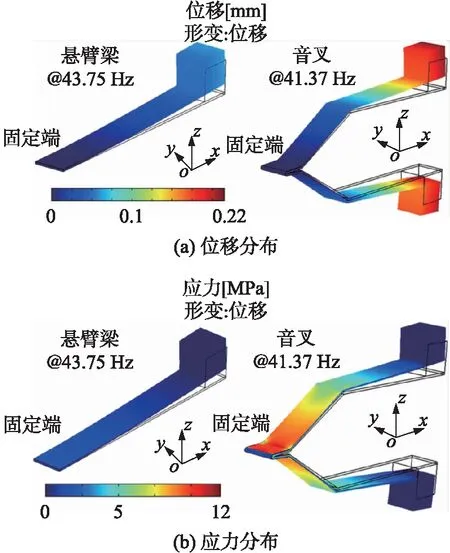
图2 悬臂梁与音叉主谐振态下
2 实验样品制作及实验设置
压电复合音叉式电流传感器的制作:分别将两块压电片及永磁铁粘贴在音叉的固定端附近及自由端处。其中音叉由一块铜片加工而成,其规模为长102 mm、宽6 mm、厚0.4 mm;并且保证两臂尽量一致,两音叉臂的各段长度为4 mm(l1)、16 mm(l2)、30 mm(l3),两臂沿z轴方向的最大间距为d=17 mm。永磁铁选用剩磁为1.2 T,大小为6 mm×6 mm×6 mm的NdFeB磁铁,且一对同极性磁铁以环氧树脂胶粘的方式固定在音叉臂自由端。压电片选用PZT-8压电板,尺寸为10 mm×6.0 mm×0.2 mm,同样以环氧树脂胶粘的方式固定在音叉固定端。具体制作的压电复合音叉式传感器样品如图1(b)所示。此外,作为对比实验制作了压电悬臂梁式电流传感器样品,其由悬臂梁、压电片及永磁铁组成,压电片和永磁铁用环氧树脂胶分别粘贴在悬臂梁固定端附近和自由端。悬臂梁由规模为的铜片46 mm×6 mm×0.4 mm加工而成,压电片及永磁铁选择与压电复合音叉式电流传感器一样。
在实验中,由函数发生器Tektronix AFG3021B提供电信号输入电线,并在电流回路内串联5.0 Ω电阻作为电流量监测电阻。函数发生器发出的电信号频率变化范围选为10 Hz~70 Hz。对于电流传感器的压电输出,若信号较大(>100 mV),则选用示波器读取;若较小(<100 mV),则选用锁相放大器测量。所有的实验均在室温和室压下完成。
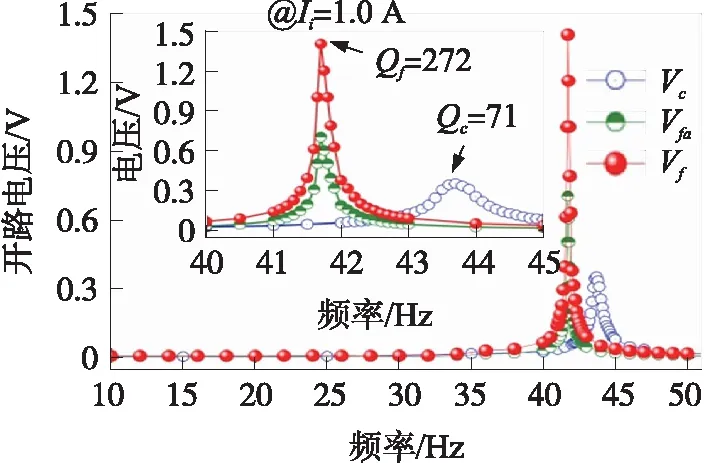
图3 压电复合悬臂梁输出电压(Vc)与压电复合音叉单臂输出电压(Vfa)及双臂串联输出总电压(Vf)与电流频率的关系曲线
3 实验结果及分析
实验测量了压电复合悬臂梁式电流传感器与压电复合音叉式电流传感器开路输出电压与输入电流频率的关系,如图3所示。当输入电流大小为1.0 A时,压电悬臂梁和压电复合音叉单臂的最大开路输出电压分别为0.35 V、0.70 V,谐振频率分别为43.8 Hz、41.7 Hz。因为压电复合音叉结构的谐振机械Q值为272,其几乎是压电悬臂梁结构的3.8倍,所以压电复合音叉结构单臂的电压输出几乎是压电悬臂梁的2倍。为了获得更高的灵敏度,可以将压电复合音叉的双臂压电片串联,这时压电复合音叉输出总电压为1.41 V,则电流灵敏度可达1.41 V/A,几乎为压电悬臂梁式电流传感器的4.0倍。这是由于音叉结构中双臂之间的谐振振动耦合作用导致的。
为了研究压电复合音叉式电流传感器的负载特性,我们保持输入电流大小为1.0 A并测量压电悬臂梁式、压电复合音叉式电流传感器谐振输出总电压与负载阻值的关系,如图4所示。从该图中可知,随之负载阻抗的增加,压电悬臂梁式、压电复合音叉式电流传感器的谐振输出电压先急剧增大再缓慢增加。当负载阻值=0.5 MΩ、1.0 MΩ、2.0 MΩ、5.0 MΩ时,压电复合音叉式电流传感器的谐振输出电压分别为0.483 V、0.744 V、1.155 V、1.296 V,分别是压电悬臂梁式电流传感器谐振输出电压的2.45倍、2.77倍、3.49倍、3.69倍。由此可见,压电悬臂梁式电流传感器具有更强的负载能力。
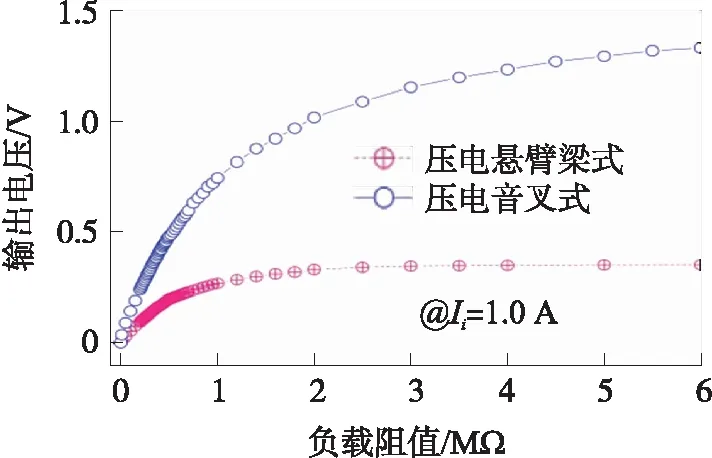
图4 压电悬臂梁与压电复合音叉式电流传感器谐振输出总电压与负载阻值关系曲线
为了进一步地考察压电复合音叉式电流传感器的线性度特性,我们测量了当输入电流大小在0.005 A~3.0 A范围内变化且负载电阻为10 MΩ时传感器的谐振输出总电压。如图5所示,在0.005 A~3.0 A的输入电流变化范围内,压电复合音叉式电流传感器的谐振输出电压从0.007 V到4.20 V变化,平均灵敏度为1.393 V/A,线性度约为0.57%。实验结果表明,该压电复合音叉式电流传感器具有高的灵敏度和良好的线性度。
5 结语
本文提出一种高灵敏度、低频的压电复合音叉式电流传感器,其主要由压电片、弹性音叉和永磁铁组成。由于压电片具有高机电耦合系数、高电压输出且机械音叉的高Q值特性有效地减少了磁-机-电转换过程中的能量损耗,因此提出的压电复合音叉式电流传感器在谐振态具有较高的灵敏度。实验结果表明压电复合音叉式电流传感器:①与压电复合悬臂梁式电流传感器相比,具有高达4.0倍的灵敏度,在负载电阻为10 MΩ、频率为41.7 Hz时,灵敏度可达1.393 V/A;②具有良好的线性度,约为0.57%。此外,该传感器结构组成简单、安装方便,只需把组件粘合即可。压电复合音叉式电流传感器在微弱电流/振动/磁场探测、磁场能量采集领域具有潜在应用价值。
[1] Braudaway D W. Precision Resistors:A Review of the Techniques of Measurement,Advantages,Disadvantages,and Results[J]. IEEE Transactions on Instrumentation and Measurement,1999,48(5):884-888.
[2] Metwally I A. Self-Integrating Rogowski Coil for High-Impulse Current Measurement[J]. IEEE Transactions on Instrumentation and Measurement,2010,59(2):353-360.
[3] 龙祖利. 小型大电流Rogowski线圈设计及性能[J]. 高电压技术,2007,33(7):79-83.
[4] Popovic R S. Hall-Effect Devices[J]. Sensors and Actuators,1989,17(1-2):39-53.
[5] Kim H G,Kang G B,Nam D J. Coreless Hall Current Sensor for Automotive Inverters Decoupling Cross-Coupled Field[J]. Journal of Power Electronics,2009,9(1):68-73.
[6] Akinci T C. Time-Frequency Analysis of the Current Measurement by Hall Effect Sensors for Electric Arc Welding Machine[J]. Mechanics,2010,5(85):66-70.
[7] Kirkam H. Optical Current Transducers for Power-Systems—A Review[J]. IEEE Transactions on Power Delivery,1994,9(4):1778-1788.
[8] Binasch G,Grunberg P,Saurenbach F. Enhanced Magnetoresistance in Layered Magnetic-Structures with Antiferromagnetic Interlayer Exchange[J]. Physical Review B,1989,39(7):4828-4830.
[9] Dogaru T,Smith S T. Giant Magnetoresistance-Based Eddy-Current Sensor[J]. IEEE Transactions on Magnetics,2001,37(5):3831-3838.
[10] Kawshima K,Kohzawa T,Yoshida H. Magneto-Inductive Effect in Tension-Annealed Amorphous Wires and MI Sensors[J]. IEEE Transactions on Magnetics,1993,29(6):3168-3170.
[11] Rheem Y W,Kim C G,Kim C O. Current Sensor Application of Asymmetric Giant Magnetoimpedance in Amorphous Materials[J]. Sensors and Actuators A:Physical,2003,106(1-3):19-21.
[12] Leland E S. A MEMS Sensor for AC Electric Current[D]. Berkeley:University of California,Berkeley,2009.
[13] Leland E S,Wright P K,White R M. A MEMS AC Current Sensor for Residential and Commercial Electricity End-Use Monitoring[J]. Journal of Micromechanics and Microengineering,2009,19(9):094018.
[14] Wang D F,Isagawa K,Kobayashi T. Passive Piezoelectric DC Sensor Applicable to One-Wire or Two-Wire DC Electric Appliances for End-Use Monitoring of DC Power Supply[J]. Microsystem Technologies,2012,18(11):1897-1902.
[15] 贾雅娜,王文. 基于磁致伸缩效应的声表面波电流传感器敏感机理分析[J]. 传感技术学报,2017,30(9):1310-1317.
[6] He W. Note:A High-Sensitivity Current Sensor Based on Piezoelectric Ceramic Pb(Zr,Ti)O3and Ferromagnetic Materials[J]. Review of Scientific Instruments,2014,85(2):026110-1-026110-3.
