钢桥面顶板与纵肋焊接细节典型疲劳裂纹三维扩展数值模拟

矣志勇

(西南交通大学，四川成都 610031)

正交异性钢桥面板由于具备自重轻、承载能力高、施工周期短、适用范围广等优点，常用作现代钢桥首选桥面板结构。然而，正交异性钢桥面板的疲劳问题较为突出，顶板与纵肋焊接细节是其诸多疲劳易损细节中的一类典型代表[1-2]。本文以顶板与纵肋焊接细节典型疲劳裂纹为研究对象，分别研究顶板与纵肋焊接细节萌生于焊根和焊趾的疲劳裂纹扩展特性。

1 顶板与纵肋典型疲劳裂纹三维扩展模拟方法

1.1 顶板与纵肋焊接细节疲劳裂纹模式

顶板与纵肋焊接细节4种典型疲劳裂纹模式如图1所示。研究表明，通过设置合理的焊缝熔透率可以有效控制模式三、模式四疲劳裂纹的开展，而该细节萌生于焊根、焊趾沿顶板厚度扩展的模式一和模式二疲劳裂纹对桥面铺装和钢桥面板危害最为严重。因此本文针对研究的钢桥面板建立实体单元模型，在模型焊根(焊趾)引入初始裂纹(图2)，用于模式一、模式二典型疲劳裂纹三维扩展模拟，从而进行相应的疲劳裂纹扩展特性研究。

图1 顶板与纵肋焊接细节疲劳裂纹

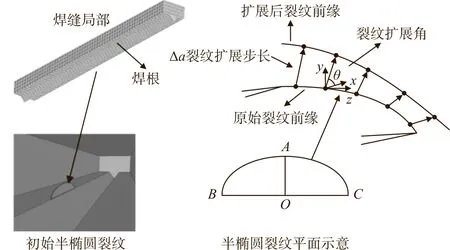
图2 三维断裂力学分析方法

1.2 三维裂纹扩展关键问题

三维裂纹扩展综合考虑张开型(Ⅰ型)、滑开型(Ⅱ型)、撕开型(Ⅲ型)3种开裂模式的作用，裂纹扩展角度依据最大周向应力理论[3]，由下式求得：

(1)

式中：υ为泊松比，本文取0.3；△KⅠ、△KⅡ、△KⅢ为Ⅰ型、Ⅱ型、Ⅲ型裂纹应力强度因子幅值。对于典型疲劳裂纹可以采用等效应力强度因子来计算裂纹疲劳寿命，本文参照规范BS7910[4]给出的计算公式求解等效应力强度因子△Keff：

(2)

式中的符号含义与式(1)相同。裂纹扩展过程中，首先确定裂纹前缘最深点扩展步长，如图2中的A点，其他裂纹尖端点的扩展步长依据下文所述Paris公式通过裂纹前缘最深点扩展步长采用公式(3)计算：

(3)

式中：△am为裂纹前缘最深点扩展步长；△ai为其余裂纹尖端点扩展步长；△Keff(m)为裂纹前缘最深点等效应力强度因子幅值；△Keff(i)为其余裂纹尖端点等效应力强度因子幅值；n值根据Paris公式取为3。

1.3 疲劳寿命计算方法

针对疲劳裂纹扩展阶段数值模型的研究，Parise定律[5-6]简单实用且不失精度因而得到广泛应用，其认为在裂纹扩展速率与裂纹尖端应力强度因子之间存在如下关系：

da/dN=C(ΔKeff)m

(4)

式中：a为裂纹尺寸；N为应力循环次数；△Keff为裂纹尖端的等效应力强度因子幅值；C和m为裂纹扩展的材料相关参数。依据BS7910[4]给出的材料参数推荐值，取C=5.21×10-13N·mm-3/2，m=3。结合Parise定律，随裂纹扩展，疲劳寿命可由下式进行计算：

(5)

2 有限元分析模型的建立

2.1 模型建立

建立单跨5U肋正交异性钢桥面板计算模型用于顶板与纵肋焊接细节典型疲劳裂纹三维扩展模拟，如图3所示。模型顶板厚16 mm，高800 mm,横隔板中心距为2 500 mm，U肋尺寸为300 mm×280 mm×8 mm。

图3 计算模型简图(单位：mm)

利用ANSYS实体单元建立的有限元模型如图4所示，在该模型中切分出用于裂纹扩展分析的局部有限元模型，局部模型用于裂纹的插入更新，通过其建立裂纹并与剩余整体模型通过节点耦合连接形成裂纹分析模型，实现典型疲劳裂纹三维扩展模拟。有限元模型约束隔板底部对应节点平动自由度，轮载横向加于关注焊接细节A-A正上方，纵向加载位置见图3所示。轮载按JTG D64-2015《公路钢结构桥梁设计规范》选取，加载面积为600 mm×200 mm,大小为60 kN。

图4 有限元模型

2.2 初始裂纹及裂纹扩展步长

本文初始裂纹型式均取为半椭圆形裂纹，如图1所示，半椭圆形裂纹尺度为椭圆长半轴OB=OC=1 mm，椭圆短半轴OA=0.2 mm。初始裂纹的插入位置为关注焊接细节A-A焊根(焊趾)位置的正上方，关于焊接细节A-A纵向对称放置。为便于后续典型疲劳裂纹三维扩展特性的分析，焊根、焊趾处疲劳裂纹均按相同扩展步模拟裂纹扩展过程。裂纹前缘最深点扩展步定义如下：裂纹扩展总步数为40步，前10步步长为0.2 mm，后20步步长为0.4 mm，最后10步步长为0.6 mm。

3 典型疲劳裂纹三维扩展分析结果

3.1 应力强度因子分析

对顶板与纵肋焊接细节典型疲劳裂纹三维扩展进行模拟，得到裂纹前缘最深点A及裂纹表面裂尖关注点B的Ⅰ型应力强度因子和复合型有效应力强度因子随裂纹扩展的变化规律如图5所示。

图5 应力强度因子

研究点A、B应力强度因子的变化规律表明：随裂纹沿顶板厚度方向扩展，A点应力强度因子呈现先增大后减小的变化趋势，B应力强度因子则随裂纹扩展而增大，其增幅则随裂纹扩展而逐步趋于平稳；就应力强度因子而言，Ⅰ型裂纹在典型疲劳裂纹的扩展过程中占主导地位，Ⅱ、Ⅲ型裂纹对其影响较小。

3.2 裂纹形态

该细节疲劳破坏模式一、模式二下三维裂纹扩展的裂纹前缘形态如图6所示。两种裂纹模式在三维扩展下的裂纹面形态是非平面的，裂纹面在扩展过程中发生了一定的角度偏转。上述研究结果表明：模式一、模式二裂纹的三维扩展，Ⅱ、Ⅲ型裂纹对裂纹扩展空间方向有重要影响，顶板与纵肋焊接细节典型疲劳裂纹三维扩展应考虑Ⅰ、Ⅱ、Ⅲ型裂纹的影响。

3.3 疲劳寿命

对特定扩展步下顶板与纵肋焊接细节典型疲劳裂纹扩展的疲劳寿命进行分析，结果如图7所示。计算结果表明：在沿顶板厚度方向达到相同裂纹深度的条件下，裂纹模式一所需要的荷载循环次数要低于裂纹模式二。而在荷载循环次数相同的条件下，裂纹模式一沿顶板厚度方向的扩展深度要大于裂纹模式二沿顶板厚度方向的扩展深度；顶板与纵肋焊接细节在焊根部位的疲劳性能相对于焊趾部位较差，该细节抗疲劳设计应重点关注焊根部位的受力状况，尽可能改善和提高顶板与纵肋焊接细节焊根部位的受力特性。

(a)裂纹模式一

(b)裂纹模式二图6 三维裂纹扩展裂纹前缘形态

4 结论

通过对顶板与纵肋焊接细节典型疲劳裂纹的三维扩展进行模拟，得出如下结论：

(1)随裂纹扩展，裂纹前缘不同位置下应力强度因子变化规律有所区别；Ⅰ型裂纹对典型疲劳裂纹应力强度因子显著，Ⅱ、Ⅲ型裂纹对裂纹面的偏转及裂纹面空间形态有较大影响，分析过程中不可忽略。

(2)顶板与纵肋焊接细节焊根部位的疲劳性能低于焊趾部位的疲劳性能，焊根部位更易于发生疲劳开裂破坏，在抗疲劳设计中应加以重视。

图7 关注点A疲劳寿命