浅谈气动阻尼识别方法

饶明航, 谷任奇, 李红义

(西南交通大学，四川成都 610031)

流体对结构振动造成阻碍并消耗其能量，这一影响结构振动的气动力参数称为气动阻尼[1]。气动阻尼受结构外形、风场特性、风速等很多因素影响，产生机理十分复杂。气动阻尼的理论解析和数值风洞研究都有一定难度，而风洞试验是目前研究气动阻尼的常用手段。风洞试验研究的关键问题之一就是如何从试验数据中准确识别气动阻尼，传统的阻尼识别方法主要分为两类：谱分析方法、时间序列法[2]。其中时间序列法里的随机减量法在气动阻尼识别上应用较多，但是对于多自由度系统，随机减量法会混有多阶模态和噪声信号。因此，随机减量法常与其他方法相结合来识别气动阻尼，其中Hilbert-Huang变换(Hilbert-Huang transform,简称HHT)和小波变换是研究最多的两种气动阻尼识别方法。另外，大多的阻尼识别方法包括随机减量法，都无法确定阻尼比的识别精度，而谱分析方法中的快速贝叶斯FFT则可以通过阻尼的后验变异系数确认识别精度[3]。

因此，本文首先对谱分析方法和时间序列法这两类方法进行了介绍和分析；其次，对以随机减量法为基础的HHT和小波分析进行了详细介绍，并进行分析和比较；最后，对谱分析方法中快速贝叶斯FFT方法进行了详细阐述和分析。

1 气动阻尼识别方法

气动阻尼是通过识别结构自身阻尼和总阻尼，再由总阻尼减去自身阻尼得到的。传统的阻尼识别方法主要分为谱分析方法和时间序列法[2]。谱分析方法包括：谱距法、谱曲线拟合法、半功率带宽法、对数递减法、快速贝叶斯FFT等。时间序列法又包括：最大熵法、自回归法、自相关衰减法、特征系统实现法、随机子空间法以及随机减量法等。

1.1 谱分析方法

对有限时长信号进行傅里叶变换的谱分析方法必然会有误差。选择较长的数据是减小谱分析方法误差的有效办法，但是这又会降低精度。因此，需要通过增加自由度、合并相邻的谱估计、对几个谱估计进行整体平均等方法来提高谱分析方法的精度。由于较长数据的不稳定性，运用这些方法时通常需要通过曲线拟合来保证谱估计值的平滑性，如Breukelman[4]和Jones等[5]分别采用最大似然估计和最小二乘法对单自由度系统谱估计进行了拟合。但是Jeary[6]指出，曲线拟合适用于线性系统，却无法反映非线性系统的特征。

1.2 时间序列法

时间序列法相比较于谱分析方法，不存在短数据的分辨率不足问题和长数据的不稳定性问题。但是文献[7-9]指出，这一方法对模态阶数十分敏感，以自回归模型为例，模态阶数太少可能得不到主峰值，而模态阶数太多又会产生伪峰值。因此，选择合适的模态阶数才能通过时间序列法得到比较精确的阻尼。

时间序列法中的随机减量法是目前评估风振结构阻尼较多的一种方法。Cole[10]在1969年提出了随机减量法，基本思想是：从零平均随机激励产生的响应采集样本，保证每个样本的初始条件相同；再对样本进行整体平均，消除了外界激励引起的响应，进而得到相同初始条件的自由振动响应；最后对自由振动响应进行结构阻尼的评估。谱分析方法大都要求信号是平稳的和线性的，而随机减量法不仅可以进行线性结构的阻尼评估，也适用于非线性结构[11]。Jery[11]采用随机减量法对已有的几个非线性结构风振响应的信号进行阻尼评估，得到的阻尼与公认正确的结论吻合良好。

对于多自由度系统信号，采用随机减量法通常会混有多阶模态和噪声信号。另一方面，大多的阻尼识别方法包括随机减量法，都无法确定阻尼比的识别精度。因此，本文将对目前较为前沿的HHT方法、小波变换以及快速贝叶斯FFT进行阐述分析，其中HHT和小波变换都是与随机减量法相结合来识别气动阻尼的。

2 Hilbert-Huang变换

Huang[12]在1998年提出的一种分析非线性非平稳信号、具有自适应性的处理方法，即Hilbert-Huang变换。这一方法由经验模态分解法(Empirical mode decomposition，简称EMD)和希尔伯特变换(Hilbert transform，简称HT)两部分组成。

2.1 经验模态分解法

对信号进行EMD处理，可以使信号平稳化，并产生一组具有不同特征尺度的序列，即本征模函数(intrinsic mode Function，简称IMF)。EMD的具体步骤是：分别对信号X(t)的极大值和极小值进行三次样条曲线拟合，形成上下包络线。将上下包络线进行整体平均，得到均值m1(t)，再用X(t)减去m1(t)得到新的序列h1(t)：

h1(t)=X(t)-m1(t)

(1)

重复以上过程k次，若mk(t)趋近于零，就获得了第一个IMF分量C1(t)：

C1(t)=hk(t)=hk-1(t)-mk(t)

(2)

用原始序列X(t)减去C1(t)得到剩余项r1(t)，再对r1(t)重复上述平稳化过程，就可以获得第二个IMF分量C2(t)，如此重复直到余项rn(t)不能再被分解为止。最后原始序列X(t)可以表示为n个IMF分量和余项：

(3)

2.2 希尔伯特变换

通过HT对信号进行处理，可以得到信号幅值和频率随时间变化的关系[13]。对信号δ(t)进行希尔伯特变换可得：

(4)

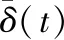
(5)

式中：a(t)为幅值函数，θ(t)为相位角函数：

a(t)=Ae-ξω0t

(6)

θ(t)=ωdt+φ0

(7)

对式(6)进行对数变换可得：

Ina(t)=InA-ξω0t

(8)

HHT识别气动阻尼的具体步骤为：先对原始数据进行EMD分解；再将关心的IMF分量用随机减量法处理，得到自由衰减曲线；最后对自由衰减曲线进行希尔伯特变换，并对结果进行最小二乘拟合求得阻尼比。

孙旭峰[14]和楼文娟等[15]采用HHT和随机减量法相结合的方法，分别识别了肋环型索穹顶结构和大跨度柔性屋盖结构的气动阻尼，表明HHT适用于大跨度这种非线性结构，可以较好的分析非线性非平稳信号。但是使用HHT识别结构参数会有以下问题：(1)在低频段产生不期望的本征模函数[16]、难以分离微弱信号或能量小的模态[17]；(2)EMD分解过程中的端点效应会不断积累误差，以致高阶本征模函数失真[18]。为了解决第一个问题，潘峰等[19]和徐正[20]在运用HHT识别结构气动阻尼时引入了带通滤波。除此以外，还有引入间歇准则、加入伪信号等方法也可以解决第一个问题。对于端点效应问题，Huang提出采用特征波进行端点延拓，但是并没有给出确定特征波的方法[18]。

3 小波分析

小波分析是一种时频局部化方法，其窗口大小一定而形状可以改变。若平方可积的实数域L2(R)内有信号x(t)和基小波g(t)，其中g(t)满足小波允许条件，则x(t)经过小波变换可得小波系数W(a,t)。

(9)

式中：a为尺度因子，*表示共轭。模态参数识别通常采用复Morlet小波，主要是因为复Morlet小波实部和虚部的幅值函数与结构的自由响应信号有相同的函数形式，且复Morlet小波不存在尺度函数，可以实现任意时频域的分辨率，对密集模态的识别效果较好[21]。复Morlet小波的时域表达形式如下：

(10)

其中fc为中心频率，fb为带宽频率。对式(10)进行傅里叶变换，可得复Morlet小波频域表达形式为：

G(af)=e-π2fb(af-fc)2-e-π2fb((af)2+fc2)

(11)

(12)

G(af)=e-π2fb(af-fc)2

(13)

对式(13)取极值可知因子a=fc/f。假设结构为有N个节点的多自由度粘性阻尼系统，其自由响应信号为：

(14)

其中Ak为第k阶模态幅值；θk为相位角；fk、fdk和ξk分别为第k阶的无阻尼频率、有阻尼频率和阻尼比，且满足：

(15)

将式(12)、式(14)代入式(9)中可得：

(16)

由第k阶尺度因子ak=fc/fk可得：

(17)

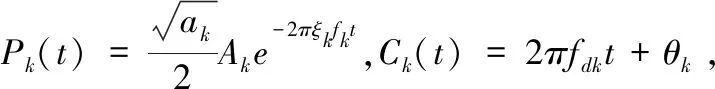
(18)

ξk=-λ1/(2πfk)

(19)

当采用小波分析识别结构气动阻尼时，首先通过随机减量法得到结构的自由衰减曲线，再进行小波分析，按上述方法得到阻尼比。

文献[22-23]联合采用随机减量法和小波变换，对结构的模态参数进行了识别，从而成功的引入了新的时频分析方法。吴海洋等[24]正是运用这一方法识别了一多自由度高层建筑的气动阻尼，表明基于随机减量法的小波分析适用于多自由度结构的气动阻尼识别。在模态参数分析的过程中，小波分析会产生边界效应问题。针对这一问题，吴海洋等[24]从实用角度出发，除去端部而只取中间数据进行分析，较好的识别了气动阻尼。另外，Kijewski等[23]详细分析了边界效应问题，提出在端部增补数据来减少边界效应的影响。

小波变换和HHT变换都是处理非平稳非线性信号的时频分析方法，与随机减量法相结合都可用于识别结构的气动阻尼。HHT变换不需要任何的先验知识，具有良好的自适应性，但是没有完善数学基础，同时存在模态混淆和端点效应问题。小波变换则具有完善的数学基础，可以对信号进行详细的时频分析和多分辨率分析，但存在边界效应问题。

4 快速贝叶斯FFT方法

Yuen和Katafygiotis[25-27]提出了基于贝叶斯快速傅里叶变换(Bayesian Fast Fourier Transform, Bayesian FFT)的模态参数识别方法。这一方法有以下几个难点：(1)自由度和模态参数的增加导致求解目标函数时会涉及到一个病态矩阵的逆矩阵；(2)模态参数的最佳估计需要求解的数值优化问题维度过多；(3)三是需要通过有限差分法来确定Hessian矩阵，这些难点使得该方法的应用受到很大的限制[28]。针对这些难点，Au[28]提出了快速贝叶斯FFT(Fast Bayesian FFT)方法。该方法是对某一共振频率带上的单一模态进行分析，因此不需要考虑自由度的数量，并且模态参数的最佳估计和Hessian矩阵可以分别通过求解一个四维数值优化问题和对数似然函数的二阶导数来确定。Au等[29]运用快速贝叶斯FFT方法识别了一个主-次结构的模态参数。

快速贝叶斯FFT方法将加速度响应表示为：

(20)

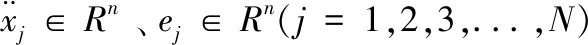
(21)

式中：i2=-1，Δt为釆样时间间隔，Fk和Gk为傅里叶变换的实部及虚部，由于采样通道的电压偏置和傅里叶变换共轭等原因，仅取k=2,...,Nq，Nq=int[N/2]+1。

根据贝叶斯理论，后验概率密度函数PDF可以由对数似然函数L(θ)表示：

p(θ|{Zk})∝exp[-L(θ)]

(22)

L(θ)= -nNfIn2+(n-1)NfInSe

(23)

θ为模态参数，包括自振频率f、阻尼比ξ、振型Φ、功率谱密度S以及预测误差的谱密度Se，Nf为计算模态相应频段上的离散频率值，k为对应频带内傅里叶变换所对应的值，并且有：

(24)

(25)

(26)

通过对式(23)的无约束优化就可以求得阻尼比，而后验不确定性可通过后验协方差矩阵来计算，其大小可以根据各自的后验变异系数来进行衡量。

快速贝叶斯FFT方法已被国内外多次用来识别结构模态参数，并且该方法还可以评估参数识别结果的不确定性。黄铭枫[30]采用快速贝叶斯FFT方法对高层结构气动阻尼进行了识别并与HHT方法识别的结果进行了对比，两者识别出的阻尼较为接近。在采用快速贝叶斯FFT方法识别气动阻尼时，需要注意两点[3]：一是选择不同共振频率带会得到不同的阻尼比识别结果，因此需要多选择几次才能得到理想的结果；二是采样数据尽量要多一些，识别精度会有所增加。

由于快速贝叶斯FFT是直接对原始数据进行傅里叶变换，并考虑了统计估计误差，因此其在识别阻尼比时减少了人为因素的影响。另外，大多数模态识别方法都无法确定阻尼比的识别精度，而快速贝叶斯FFT方法可以根据模态参数的后验变异系数确认各模态参数的识别精度。

5 结论

本文对传统的气动阻尼识别方法进行了阐述分析，并进一步详细地介绍了HHT、小波分析和快速贝叶斯FFT，得出以下结论：

(1)谱分析方法要求信号是平稳的和线性的，而时间序列法中的随机减量法则可以适用于非线性系统，从而可以更广泛的应用于结构的气动阻尼识别。(2)小波变换和HHT变换都是处理非平稳非线性信号的时频分析方法。HHT变换具有良好的自适应性，但是没有完善数学基础，同时存在模态混淆和端点效应问题；而小波变换具有完善的数学基础，可以对信号进行详细的时频分析和多分辨率分析，但存在边界效应问题。(3)快速贝叶斯FFT方法考虑了统计估计误差，减少了人为因素对阻尼比识别的影响，并且快速贝叶斯FFT方法可以确认对各模态参数的识别精度。