仿生四足机器人运动规划与步态转换
2018-04-11罗红艳
罗红艳,魏 莉,李 彰,曾 顺
(武汉理工大学 机电工程学院,湖北 武汉 430070)
生物经过数千年的进化,其外形结构和运动模式已经与环境达到了高度契合。他们具有最合理的结构,灵活的运动特性以及良好的适应性,可以说是生物环境下的最优状态[1]。仿生机器人在结构和运动模式上模拟生物,走在机器人前沿的BigDog[2]就是仿生机器人的代表,它可在崎岖的地面上以稳定的步态运动。步态是四足机器人的研究重点之一,它与机器人的稳定性和运动速度有直接关系。目前,研究者们对四足机器人的单一步态研究较多,包括整机稳定性的分析、足端轨迹的规划、四足之间的协调等。针对整机稳定性,研究者们提出过很多模型,如线性倒立摆模型、弹簧-阻尼模型等。足端轨迹也多种多样,赵明国[3]规划AIBO ERS-7的运动时提出了基于矩形的轨迹。Kim等[4]提出基于椭圆的轨迹。Sakakibara等[5]规划出摆线轨迹。李志[6]结合正弦轨迹与椭圆轨迹规划出类椭圆轨迹。此外,对步态转换过程也有不少研究,步态转换过程较复杂,两种步态之间需要精确的计算才能顺利转换,并且在步态转换过程中,整机协调性受到很大的考验。Liu等[7]通过改变机器狗运动时序的方法完成了步态转换。Jianhua Wang等[8]将静步态、动步态统一起来,建立数学模型,通过改变输入参数来达到改变步态的目的。Zhao等[9]基于能量消耗规划了机器人的转换步态。Koo[10]等在仿生学的启发下设计出机器人的步态转换过程。笔者针对仿生机器人,设计机器人的刚性腰部和具有平行四边形结构的四足,规划以多项式和直线结合为足端轨迹的Walk步态、以多项式为足端轨迹的Trot步态,提出四足同时改变相位与足端轨迹的转换方法,解决步态转换时的四足协调关系问题,并实现步态的快速转换,为仿生机器人的研究提供一些参考。
1 生物狗运动规律研究
为获取生物狗的运动规律,在生物狗身上标记13个点,如图1(a)所示,前足4个,分别为足端、腕关节、肘关节、肩关节;后足4个,分别为足端、踝关节、膝关节、髋关节;腰部5个分别为S1、S2、S3、S4、S5。实验中采用高速摄像机,型号为FASTCAM Mini UX100,分别在3.5 km/h、4.0 km/h、6 km/h、7 km/h 4种速度下,以500 Hz的频率对成年拉布拉多在跑步机上的运动进行多组拍摄, 其中前两种速度为静步态,后两种速度为动步态。通过PHOTRON 软件从所拍摄视频中提取标记点的位置坐标,提取出的坐标数据在MATLAB里分析处理。研究发现,动步态时各个关节角的变化范围明显大于静步态时的变化范围,图1(b)所示为7.0 km/h时,各个关节角的变化。

图1 生物狗实验与结果
从图1(b)可看出:①后腿3个关节的变化趋势与前腿3个关节的变化趋势一致;②后腿膝关节与踝关节的变化趋势与角度范围基本一致;③在运动过程中腰部角度变化不大;④髋关节角度变化范围为[150°,180°],膝关节与踝关节角度变化范围为[90°,130°]。
2 仿生机器人结构设计与运动学分析
2.1 仿生四足机器人机械结构设计
基于上一节研究生物狗所得到的规律,参考生物狗的关节连接方式和形体尺寸,设计了仿生四足机器人的机械结构。图2(a)是在三维软件SolidWorks里建立的机器人装配图,整机结构由四条腿与腰部构成。由于前腿与后腿的变化趋势基本一致,因此四足统一采用后腿的结构,由大腿肢段、小腿肢段、足部肢段3部分构成。由于后腿膝关节与踝关节的变化基本一致,因此腿部采用双平行四边形机构使膝关节和踝关节的角度一致,减少单腿的自由度,简化机构,每条腿由3个主动关节变为2个主动关节(髋关节与膝关节)和一个被动关节(踝关节)。由于运动时腰部角度变化不大,因此腰部采用无自由度的刚性腰部。整机共12个关节,8个主动关节均采用MAXON 直流无刷电机驱动,电机型号为EC45。

图2 仿生四足机器人三维模型与腿部结构
2.2 运动学分析
图2(b)为机械腿结构几何图,其中φ1、φ2分别为电机1和电机2的驱动角度,θ1、θ2、θ3分别为髋关节、膝关节和踝关节的转动角度,l1、l2和l3分别为大腿肢段、小腿肢段和足部肢段的长度,主要参数如表1所示。

表1 腿部设计主要参数
建立固连于髋部的坐标系(X,Z),足端坐标为(x,z),可得运动学正解如式(1)所示,运动学逆解如式(2)所示。

(1)
(2)
3 步态规划
步态是各腿在时间和空间上的运动顺序[11],平整地面上多为周期步态。当腿与地面接触时,腿的状态为着地相,腿在空中摆动时状态为摆动相。同一条腿到达相同状态所需时间为周期。单腿经过一个摆动相,机身质心相对于地面前进的距离为单腿步距。着地相时长与周期的比为占空比。第n条腿的着地时刻与参考腿着地时刻的差值与运动周期的比为相位差。
3.1 Walk步态规划
步态规划主要分两部分,一部分是确定各腿之间的协调关系,即确定占空比与相位差,另一部分是规划合理的足端轨迹曲线。
当四足机器人的腿从后向前运动,抬腿顺序为LF-RH-RF-LH时,其步态稳定性最高[12]。其中LF表示左前腿,RF表示右前腿,LH表示左后腿,RH表示右后腿。为使能量消耗最小,Walk步态采用相位差相等的对称步态,φLF=0,φRF=0.5,φLH=0.75,φRH=0.25。如图3(a)所示,占空比β=0.75。

图3 Walk步态规划
足端轨迹是机器人单腿足端在空间内走过的轨迹,在X、Z方向均是关于时间的函数。足端轨迹影响机器人行走时的速度及稳定性等,需满足以下条件:①轨迹平滑,无位置突变,保证机器人的行走过程平稳;②速度连续;③加速度不宜过大,否则会对足端产生较大冲击力,影响整机的稳定性;④各关节角变化连续。四足机器人以Walk步态运动时,同时有3条腿与地面接触,为保证机身相对于地面匀速运动,必须使处于着地相的3条腿相对于各自髋部的速度一致,因此在X方向着地相选用直线形式,摆动相X,Z方向均采用多项式形式,Z方向着地相时无变化,如式(3)所示。
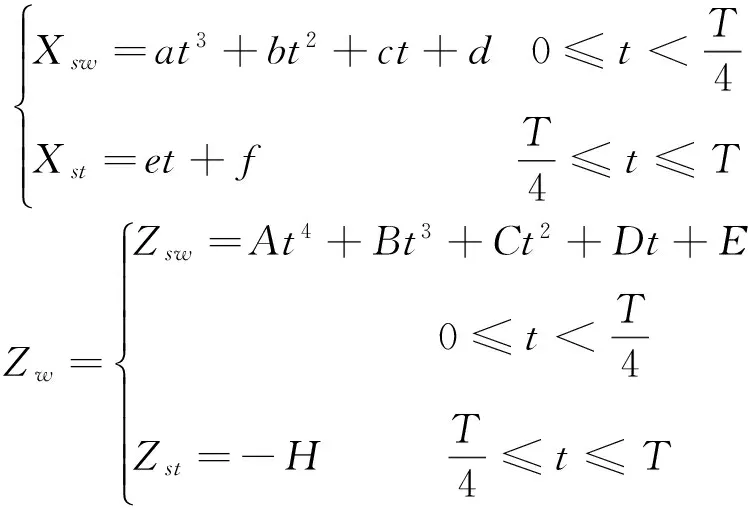
(3)
式中:sw表示摆动相,st表示着地相;a,b,c,d,e,f,A,B,C,D,E为待定系数;T为运动周期;S为单腿步距;H为髋部到单腿所在最低点的距离;h为髋部到单腿所在最高点的距离。式(3)需满足约束式(4)。故得Walk步态轨迹方程式(5),取参数S=0.15 m,T=4 s,h=0.29 m,H=0.32 m。Walk步态足端轨迹与速度变化曲线如图3(b)所示,在着地相时各足端相对于髋部为匀速运动。
(4)

(5)
3.2 Trot步态规划
对角小跑步态是稳定性极高的动步态,其对角线上的腿运动一致。选其占空比为0.5,即每个时刻都有两条腿处于着地状态,另外两条腿处于空中摆动状态,Trot步态的相位关系如图4(a)所示。Trot步态时,对角线上两足运动状态一致,着地相两足相对于各自髋部的速度是一致的,故不用考虑着地相时各足的速度问题。足端轨迹同样采用多项式,方程如式(6)所示。取参数S=0.2 m,T=4 s,h=0.29 m,H=0.32 m,Trot步态足端轨迹与速度变化如图4(b)所示。

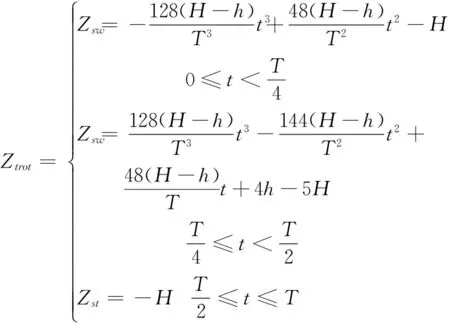
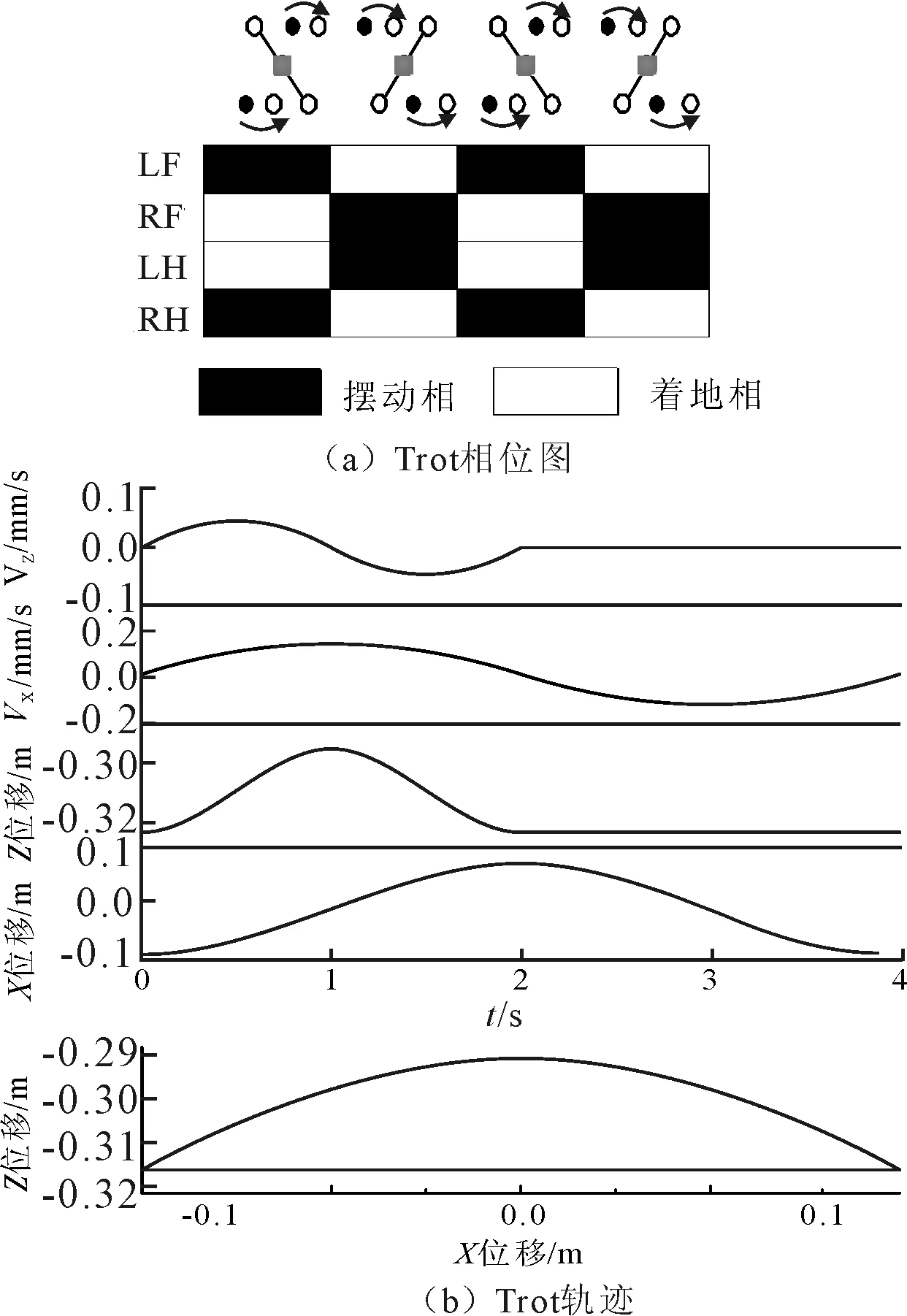
图4 Trot步态规划
3.3 转换步态规划
要实现静步态到动步态的转换,需考虑整机协调性,规划好各腿在各个时刻的状态。要达到快速转换的目的,必须缩短切换步态所需的时间。基于上述考虑,机器人采取四条腿相位与足端轨迹同时切换的方式,在半个周期内完成步态切换。图5(a)为规划的转换过程相位变化图,线框表示转换步态时各腿所处状态,线框左边为一个周期的Walk步态,右边为两个周期的Trot步态。以左前腿为参考腿,Walk步态0~T/4为Walk步态摆动相,T/4~2T/4为着地第一阶段,2T/4~3T/4为着地第二阶段,3T/4~T为着地第三阶段。开始转换时,左前腿处于着地第三阶段,右前腿处于着地第一阶段,左后腿处于摆动相,右后腿位着地第二阶段,转换开始后,各腿顺次进入下一个状态,转换步态中,各腿足端轨迹的变化如图5(b)所示。

图5 转换步态规划
0~0.5 s:LF和RH分别从Walk步态着地第三阶段和Walk步态着地第二阶段进入摆动相,RF和LH分别从Walk着地第一阶段和Walk摆动相进入转换步态着地相。
0.5~1.0 s:四只腿分别沿转换曲线运动,LF在Z方向保持在最高点,RF和LH在Z方向无运动,RH在Z方向沿曲线上升。
1.0~1.5 s:继续沿各自的转换曲线运动。
1.5~2.0 s:在时刻末,LF和RH同时进入Trot步态的着地相,相应的RF和LH变为Trot步态的摆动相。
经过2 s,四足机器人实现Walk步态到Trot步态的转换。
4 仿真
当足端轨迹曲线确定后,根据式(2)在MATLAB中分别计算Walk步态,Trot步态和转换步态的关节角度,并在ADAMS中根据所设计的机构进行建模和仿真。
ADAMS中建立的机器人模型如图6所示,由于ADAMS仿真主要是点与点之间的关系,因此将所设计的机构简化,电机与腰部连在一起,腿部由大腿肢段、小腿肢段和足端肢段组成。

图6 ADAMS中建立的机器人模型
模型建立好后,添加12个转动关节,添加驱动,将由运动学逆解得到的关节角度添加为MOTION的运动角度。地面设置为无障碍硬质地面,动摩擦系数设置为0.1,静摩擦系数设置为0.3,仿真时间设置为10 s,包括4 s的Walk步态,2 s转换步态,4 s的Trot步态。
从Walk步态到Trot步态,其质心轨迹变化如图7(a)所示。0~4 s为Walk步态,此时X方向为一条直线,质心在前进方向为匀速运动,与规划的Walk步态一致。Z方向基本无波动,4~6 s为步态切换过程,X方向和Z均有波动,在第6 s末,Z方向有2 mm的波动,这是由于此时四足的状态均发生变化,从转换步态变为Trot步态,质心需到达Trot步态过程中质心的最高点,随后进入Trot步态,至此机器人顺利从Walk步态转换到Trot步态。
步态转换过程中,足端会受到地面的冲击力,图7(b)为四腿在仿真过程中的受力,从图7(b)可看出,各腿处于摆动相时,由于足端未与地面接触,其受力均为零,在着地相状态末,足端会受到一个较大的支撑反力,这是由于在着地相末,机器人机身的质量大部分由右前腿支撑,其支撑反力的最大值为110 N。仿真过程表明,110 N的力对机器人的稳定性影响不大,其质心未因受到110 N的支撑反力而出现突变,机器人可稳定行走。
5 结论
笔者利用高速摄像机对生物狗进行了运动捕捉,参考捕捉结果、生物狗关节连接方式和结构尺寸设计了仿生四足机器人的结构,规划出Walk步态、Trot步态以及转换过程,最后在ADAMS中验证其可行性,结果表明,所设计的仿生四足机器人在规划的单一步态下运动平稳,可快速完成步态切换。
针对仿真过程中出现的质心在转换时的抖动现象,后期将分析质心的运动轨迹作为步态规划的约束条件。不仅考虑各腿之间的协调,还需考虑各腿与机身的协调问题。
参考文献:
[1]王国彪,陈殿生,陈科位,等.仿生机器人研究现状与发展趋势[J].机械工程学报,2015,51(13):27-44.
[2]Raibert M, Blankespoor K, Nelson G, et al. BigDog, the Rough-Terrain Quadruped Robot[J]. IFAC Proceedings Volumes, 2008,41(2):10822-10825.
[3]周坤玲.四足仿生机器人高速步态规划方法研究[D].北京:北京交通大学,2013.
[4]Kim K Y, Park J H. Ellipse-based Leg-trajectory Generation for Galloping Quadruped Robots[J]. Journal of Mechanical Science & Technology, 2008,22(11):2099-2106.
[5]Sakakibara Y, Kan K, Hosoda Y, et al. Foot Trajectory for a Quadruped Walking Machine[C]∥ IEEE International Workshop on Intelligent Robots and Systems.[S.l.]: IEEE, 2002:315-322 .
[6]李志.液压四足机器人机构分析及对角稳定步态规划[D].南京:南京航空航天大学,2014.
[7]Liu A, Zhang X Y, Zhang K G. Gait Transition of Quadruped Robot Using Time Sequence Control Based on Finite-state Machine[J]. Applied Mechanics & Materials, 2013,423-426:2799-2804.
[8]Wang J, Wen J, Chen W, et al. A Gait Generating Algorithm with Smooth Speed Transition for the Locomotion of Legged Robots[J]. Transactions of the Institute of Measurement & Control, 2014,36(2):260-275.
[9]Zhao D, Jing X U, Dan W U, et al. Gait Definition and Successive Gait-transition Method Based on Energy Consumption for a Quadruped[J]. Chinese Journal of Mechanical Engineering, 2012,25(1):29-37.
[10]Koo I M, Trong T D, Lee Y H, et al. Biologically Inspired Gait Transition Control for a Quadruped Walking Robot[J]. Autonomous Robots, 2015,39(2):169-182.
[11]王鹏飞. 四足机器人稳定行走规划及控制技术研究[D]. 哈尔滨:哈尔滨工业大学, 2007.
[12]Song S M, Waldron K J. Machines that Walk: The Adaptive Suspension Vehicle[J]. Nasa Sti/Recon Technical Report A, 1989, 89(6):7-12.
