一种低复杂度的椭圆球面波调制信号预失真方法
2018-04-11刘传辉缪幸吉陆发平康家方李笔锋
刘传辉,缪幸吉*,陆发平,康家方,李笔锋
(1.海军航空大学 航空作战勤务学院,山东 烟台 264001;2.山东省信号与信息处理重点实验室,山东 烟台 264001;3.中国人民解放军92768部队,广东 汕头 515828)
0 引言
随着社会发展,信息业务和用户规模不断扩大,对卫星通信系统信息传输速率要求越来越高;但频谱资源作为稀有资源,与日益增长的信息传输速率需求之间的矛盾更加突出。因此,如何提高系统频带利用率成为人们关注的焦点。基于椭圆球面波(Prolate Spheroidal Wave Function,PSWF)的非正弦时域正交调制方法[1]是一种高能量聚集性和高频带利用率的新型调制技术,采用多路并行脉冲信号传递信息,可以使频带利用率快速逼近2 Baud/Hz,为提高卫星通信系统信息传输速率提供了一种可行方案。但由于PSWF调制信号由多路脉冲信号叠加而成,其峰均功率比较高[2],易受功率放大器(Power Amplifier,PA)非线性特性影响,造成调制信号非线性失真,导致系统误码性能降低[3],限制了PSWF调制信号在卫星通信系统中的运用。因此,为了保证系统误码性能,需对调制信号进行预失真处理,补偿调制信号的非线性失真。
目前,数字预失真技术[4]因其具有适用频带宽、准确度高、稳定性好和成本低等优良特性,在通信系统中得到广泛运用。数字预失真技术主要分为基于查询表(Look-up Table,LUT)预失真技术和基于多项式的预失真技术。针对LUT预失真方法的算法复杂度高的问题,艾勃从改进对第二维查找表的索引[5]的角度出发,吴长奇从加快查表法收敛速度[6]的角度出发,分别对LUT预失真方法进行优化,降低了LUT预失真方法算法复杂度。与LUT预失真方法相比,基于多项式的预失真方法能够节省大量RAM存储资源,更易于工程实现,但仍存在算法复杂度高的问题。钱业青结合预失真技术的特点,建立了非线性抽头延时多项式模型[7],提出了一种简化的Wiener功放预失真方法;黄浩在低中频预失真器构架的基础上,提出了一种基于坐标变换的预失真参数估计方法[8],有效降低了传统数字基带预失真方法的算法复杂度。相对于基于正弦波的多载波调制信号,关于PSWF非正弦调制信号的预失真方法研究较少。钟佩琳等在数字预失真技术研究的基础上,针对传统记忆多项式预失真方法算法复杂度较高的问题,结合PSWF调制信号特性进行分析,从降低预失真方法相关矩阵条件数角度出发,提出了基于压缩量化[9]和并行两箱预失真方法[10],能够有效减少功放对调制信号造成的非线性影响,但是基于压缩量化和并行两箱预失真方法,分别存在需要大量RAM存储资源和算法复杂度较高的不足。陆发平等针对PSWF调制信号预失真方法算法复杂度高,运算量大等问题,提出了一种基于递推最小二乘法(Recursive of Least Square,RLS)算法的预失真方法[11],通过降低输出方程多项式阶数,以牺牲对大幅值分量失真的补偿能力来降低算法复杂度,提高预失真器工作效率。
而对于卫星通信系统而言,预失真器作为整个系统的一部分,预失真器工作效率将直接影响整个卫星通信链路的信息传输速率。因此,有必要对低复杂度、高效率的预失真方法展开研究。本文从降低预失真算法的时间复杂度出发,考虑将调制信号解析信号表达式中的实部和虚部并行预失真处理,给出了一种低复杂度的预失真方法。仿真结果表明,本文所给的预失真方法减少了算法的时间复杂度,提高了预失真器工作效率,能够有效补偿PSWF调制信号带内和带外失真,提高了系统误码性能和改善了调制信号功率谱。
1 功放对PSWF调制信号的影响
目前,功率放大器模型分为有记忆和无记忆两类,其中记忆功放模型有Volterra模型、Hammerstein模型和记忆多项式模型。其中,记忆多项式模型与其他模型相比,具有运算量低,复杂度程度小、实现简单等优势,其表达式为[4]:
(1)
式中,K为多项式阶数,Q为记忆深度,x(t)为功放输入信号,y(t)为功放输出信号,akq表示待辨识参数。
令式参数Q=3,K=5,PSWF脉冲选取频段为10~11GHz,时间带宽积为c=8Hz·s,选取前10阶能量聚集性高的PSWF脉冲信号,在时域上叠加生成调制信号,并对信号幅值进行归一化处理。调制信号经过功放前后的功率谱和系统误码性能如图1所示。

图1 调制信号功率谱与系统误码性能
从仿真结果可知,调制信号经过功放后,由于受到功放的非线性特性影响,导致信号功率谱发生拓展,带外失真约23 dB;且由于功放的非线性特性对脉冲组间良好正交性的影响,导致系统误码性能大幅降低,这表明此时功放造成的非线性失真成为影响系统性能的主要因素。因此,为了保证良好的系统性能,必须要对调制信号进行预失真处理,降低功放对调制信号造成的非线性影响。
2 改进的预失真方法系统模型
功放对调制信号的非线性影响,导致信号产生带内和带外失真,主要表现在幅值和相位两个方面。对PSWF调制信号而言,在其解析信号表达式中有如下关系:
s(t)=|s(t)|eiθ=a(t)+ib(t),
(2)
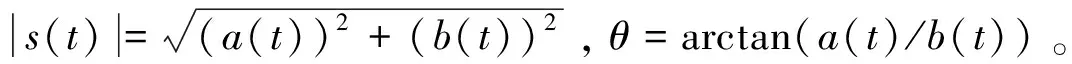
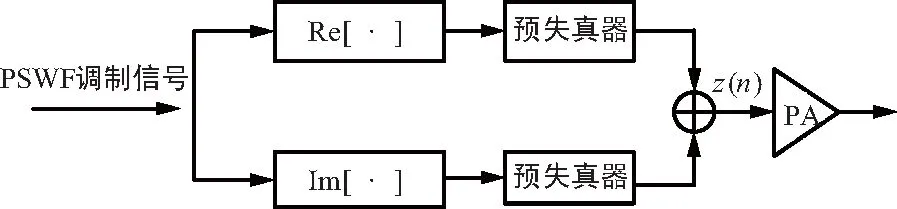
图2 改进的预失真方法原理
改进的预失真方法由上、下两路组成,分两路同时对PSWF调制信号解析信号中实部和虚部进行预失真处理,两路处理后的输出信号叠加生成预失真器的总输出z(n),再经过功放,实现对调制信号的放大处理,改进的预失真方法数学表达式为:
(3)
式中,K1和K2表示多项式阶数,Q1和Q2表示记忆深度,x(n)为调制信号,z(n)为预失真器的总输出,ak1q1和ak2q2表示待辨识参数。
根据所示原理框图,构建改进的预失真方法系统模型框图,如图3所示。
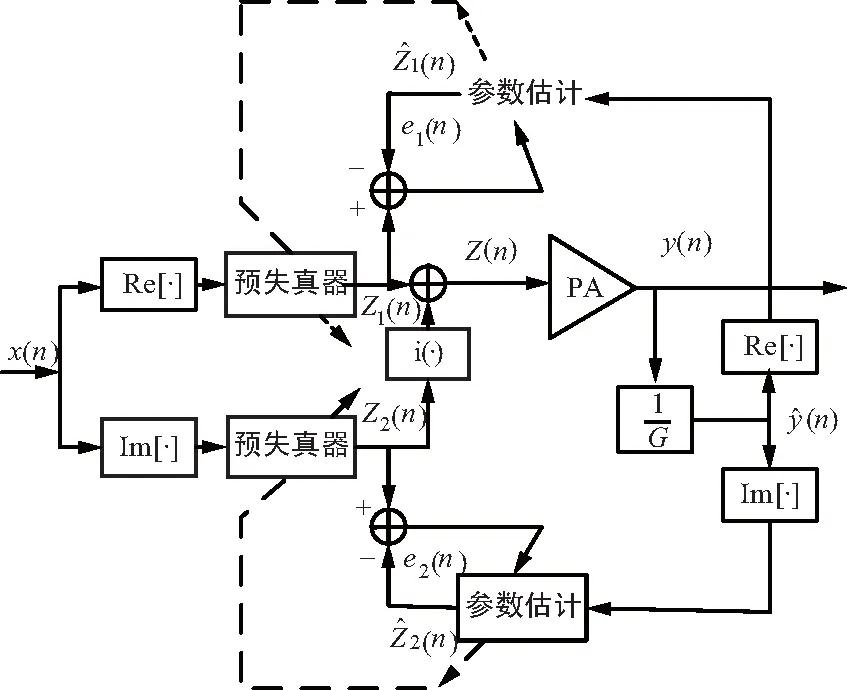
图3 改进的预失真方法系统模型
具体实现步骤如下:
① 首先对输入信号x(n)进行实部和虚部分离,再将二者并行传输,分别通过预失真器进行预失真处理。

(4)
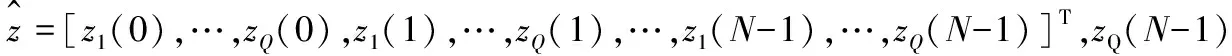
④ 将更新后的参数复制给预失真器,使预失真器参数能随着功放动态特性的改变而实时更新,保证预失真器良好的性能。
3 仿真分析
在Matlab仿真环境下,从算法的时间复杂度、预失真方法学习曲线、信号功率谱和系统误码性能4个方面,对给出的改进的预失真方法性能进行分析,验证该方法的可行性和优越性。
3.1 仿真条件
① PSWF调制信号:信号频率范围为10~11 GHz,时间带宽积c=8 Hz·s,选取前10阶能量聚集性高的PSWF脉冲信号,在时域上叠加生成调制信号。
② 功率放大器:采用记忆多项式模型,表达式如式(1),其中,多项式阶数K为5,记忆深度Q为3,参数为akq:
a10=1.0513+0.0904j,a30=-0.0542-0.2900j,a50=-0.9657-0.7028j;
a11=-0.0680-0.0023j,a31=0.2234+0.2317j,a51=-0.2451-0.3735j;
a12=0.0289-0.0054j,a32=-0.0621-0.0932j,a52=0.1229+0.1508j;
参数akq提取自实际AB类功率放大器。
3.2 仿真结果与分析
3.2.1 算法的时间复杂度
算法复杂度主要包括时间复杂度与空间复杂度,其中,算法的时间复杂度是指执行算法所需要的计算工作量,能够更加直接体现算法的复杂度。在3.1节仿真条件下,各类预失真方法处理时间如图4所示,直观反映了算法的时间复杂度,仿真结果表明,由于将信号分上、下两路并行预失真处理,降低了预失真参数维数,减少了参数估计运算的复杂度,改进的预失真方法运算时间均小于现有预失真方法的运算时间,这表明该方法能减少预失真算法时间复杂度,提高预失真器工作效率。但是,由构建的系统模型可知,改进的预失真方法是以牺牲算法空间复杂度来减小时间复杂度。

图4 预失真处理时间
3.2.2预失真方法学习曲线
是预失真方法学习曲线,反映预失真方法收敛速度和实时性优劣。仿真结果表明,采用改进的预失真方法,系统初始误差约为-34 dB,稳态误差约为-35 dB;与记忆多项式预失真方法和基于RLS算法的预失真方法相比,由于该方法预失真参数维数低,预失真参数简单易估计,收敛速度更快,系统稳态误差降低约7.5 dB;与并行两箱预失真方法相比,由于并行两箱预失真方法采用非迭代查询表和正交记忆多项式2个模块并行补偿,因此,初始误差和稳态误差都高于并行两箱预失真方法。
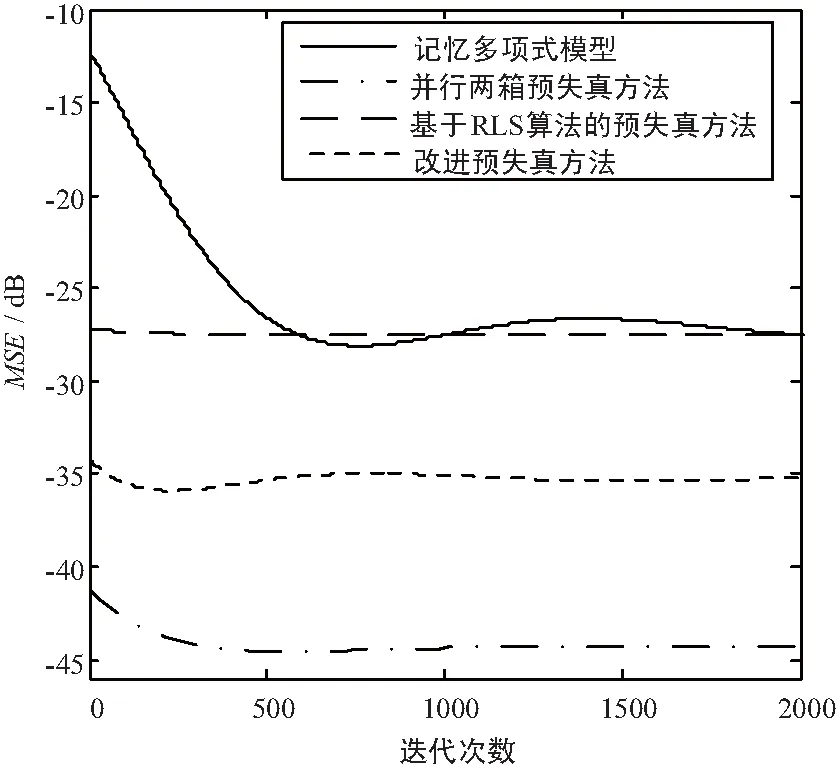
图5 预失真方法学习曲线
3.2.3信号功率谱
图6是调制信号经过预失真处理后,通过功放前后的功率谱,直观反映各种预失真方法对调制信号带外失真的补偿能力。仿真结果表明,调制信号直接经过功放后,功放的非线性特性使信号功率谱发生了拓展,带外失真达到了23 dB;调制信号经过改进的预失真方法处理后,功率谱带外失真得到了有效改善,补偿约23 dB,靠近主瓣处信号功率谱几乎与原调制信号一致;改进的预失真方法对调制信号带外失真的补偿能力均优于现有的预失真方法。

图6 信号功率谱
3.2.4系统误码性能
系统误码性能是衡量通信系统可靠性的重要指标,反映预失真器补偿调制信号带内失真的能力。图7是调制信号经过功放后,通过AWGN信道,在利用相关解调情况下,不同预失真方法处理后的系统误码率特性曲线。仿真结果表明,功放非线性特性使调制信号产生畸变和相位偏移,脉冲组间良好的正交性被破坏,解调性能恶化,系统误码率较高。经过改进的预失真方法处理后,当误码率为10-5时,与原调制信号相比,性能差距缩小至0.9 dB,调制信号的带内失真得到了有效改善。在信噪比>6 dB后,改进的预失真方法对调制信号带内失真的补偿能力略好于基于RLS算法的预失真方法和记忆多项式预失真方法;但与并行两箱预失真方法相比,性能仍存在0.8 dB的差距。

图7 系统误码率
4 结束语
针对现有的PSWF调制信号预失真方法存在算法复杂度高、工作效率低的问题,本文给出了一种低复杂度的预失真方法,构建了其系统模型,并对所提方法的各项性能进行了仿真分析。仿真结果表明,所提预失真方法能有效补偿调制信号带内和带外失真,提高了系统的误码性能并改善了调制信号功率谱;同时,算法的时间复杂度得到了有效降低,提高了预失真器工作效率,但是以增大算法的空间复杂度为代价的。该方法所采用的多项式模型最高阶数为1,对大幅值信号分量失真的补偿能力较弱,在误码率为10-5时,与原调制信号相比,误码性能还有约0.9 dB的差距,因此,下一步考虑利用并行两箱预失真方法补偿大幅值分量失真的优势,将2种预失真方法联合使用,提高系统误码性能。
[1]王红星,赵志勇,刘锡国,等.非正弦时域正交调制方法:200810159238.3[P],2009.
[2]毛忠阳,刘传辉,陆发平,等.一种新的PSWF调制信号PAPR抑制方法[J].无线电通信技术,2017,43(2): 6-11.
[3]张磊,刘传辉,王红星,等.非正弦时域正交调制系统解调性能分析[J].中国电子科学研究院学报,2012,7(2): 158-162.
[4]艾渤,李波,钟章队,等.宽带功率放大器预失真原理[M].北京:科学出版社,2011.
[5]AI B,YANG Z X,PAN C Y,et al.Improved LUT Technique for HPA Nonlinear Predistorton in OFDM Systems[J].Wireless Personal Communication,2006,38(4):495-507.
[6]吴长奇,张晓娟.基于定点迭代方法的自适应数字预失真器[J].重庆邮电大学学报(自然科学版),2011,23(5):536-539.
[7]钱业青,刘富强.Wiener功率放大器的简化预失真方法[J].通信学报,2007,28(10):55-59.
[8]黄浩,钱骅,姚赛杰,等.基于坐标变换的射频功放预失真参数估计方法[J].通信学报,2015,36(1):75-83.
[9]钟佩琳,王红星,孙小东,等.基于压缩量化的非正弦时域正交调制信号预失真方法[J].电子信息学报,2013,35(3):658-664.
[10] 钟佩琳,王红星,刘传辉,等.一种并行两箱预失真方法[J].华中科技大学学报(自然科学版),2014,42(2):86-90.
[11] 王红星,陆发平,刘传辉,等.基于RLS算法的椭圆球面波调制信号预失真方法[J].中国电子科学研究院学报,2016,11(1): 98-102.
[12] 宋杰,马忠义.算法能耗复杂度的定义与推导[J/OL].计算机工程与应用:1-14(2017-01-20) http://kns.cnki.net/kcms/detail/11.1826.TP.20170120.1053.006.html.
