过站保障车辆集中式调度的单亲遗传算法
2018-04-11朱新平韩松臣
朱新平,韩松臣
(1.中国民用航空飞行学院空中交通管理学院,四川 广汉 618307; 2.四川大学空天科学与工程学院,四川 成都 610065)
飞机过站保障是指在飞机停靠机位期间,地服部门为其提供的航油加注、行李装卸等保障服务.过站保障通常需调度各种保障车辆,其基本任务就是在车辆资源和标准作业流程约束下为飞机指派保障车辆及作业时段,尽可能减少由保障造成的航班延误.因此,飞机过站保障是保证后续航班生产按计划展开的重要工作.以往研究以过站保障流程改进为主,多采用贝叶斯网络[1]、Petri网[2-4]、AOE (activity on edge)网络[5]等方法.过站保障车辆调度问题可分为:(1) 多种车辆完成某一架飞机过站保障作业的调度[5];(2) 某种车辆完成多架飞机某一类保障作业的调度[6-10];(3) 多种车辆完成多架飞机多个保障作业的调度[11].本文研究第(3)类问题.有学者将其视为车间调度问题[8,10,12]或车辆路径规划问题[13].Leeuwen等人则采用简单时间网络建模过站保障过程,并分析保障车辆需求规模[14-15].总体来看,以往解决方法所给模型参数较多、求解复杂.
针对多架飞机多个保障作业的保障车辆调度,以集中式统一调度为背景,本文采用单亲遗传算法来求解,考虑车辆调度规则设计递阶式染色体编码结构,将过站保障作业约束和车辆指派约束以直观、易于理解的形式描述,并设计基于车辆可调度能力空间概念的染色体解码方法.
1 问题分析与建模
1.1 问题分析
过站保障过程中,车辆在未分配任务时位于停放区,分配任务后会行驶至机位作业,且不同型号车辆具有不同保障能力.过站保障车辆调度过程(如图1所示)需满足:(1) 作业时序关系约束.某些作业任务不能同时展开,应满足前后继关系约束,而有些任务可同时展开.典型作业时序关系约束见表1.(2) 车辆指派规则约束.不同机型同一类作业所需保障车辆数量及作业耗时会存在差异.某机场过站保障车辆指派规则见表2.(3) 过站时间约束.保障作业应尽量在飞机计划的过站时段内完成,以免影响下一航段飞行.由此可见,过站保障车辆调度是一类涉及多车辆协同、多作业任务串行与并发共存的调度问题.
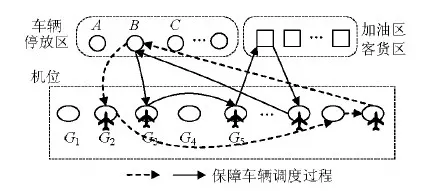
图1 飞机过站保障车辆调度过程Fig.1 Scheduling process of service vehicle for aircraft turnaround
1.2 数学模型
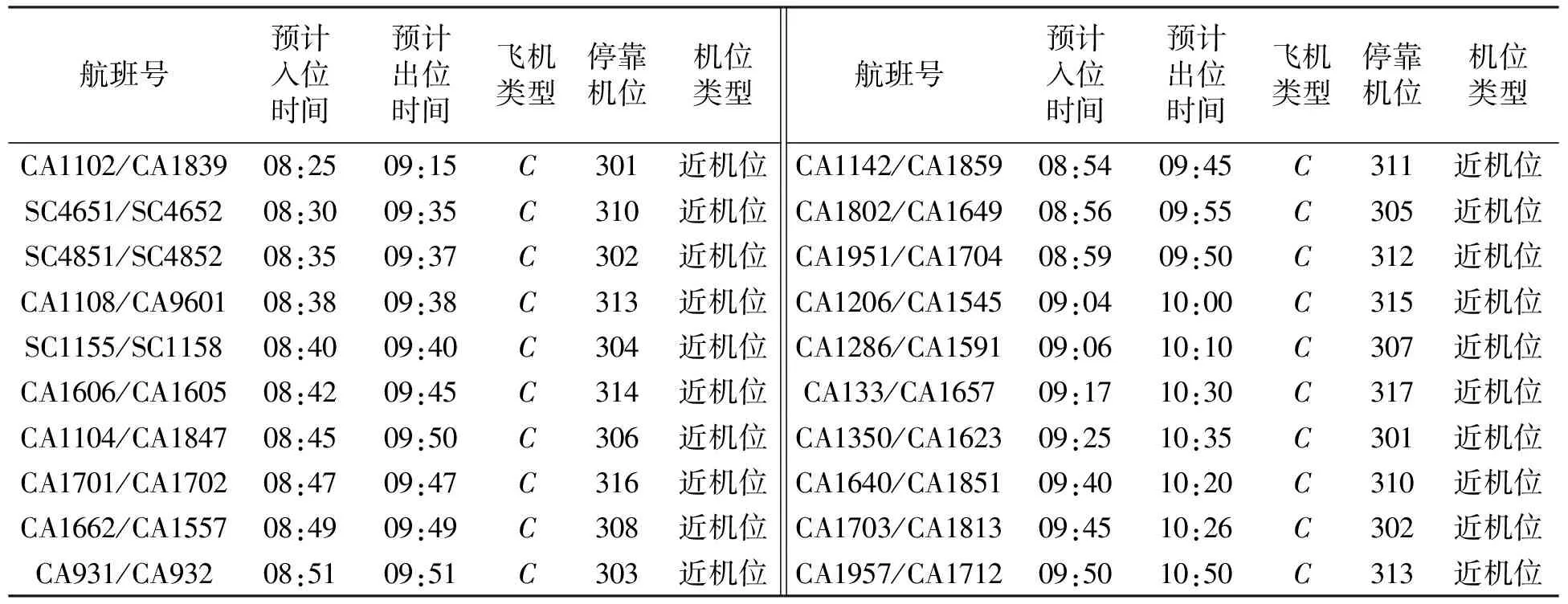
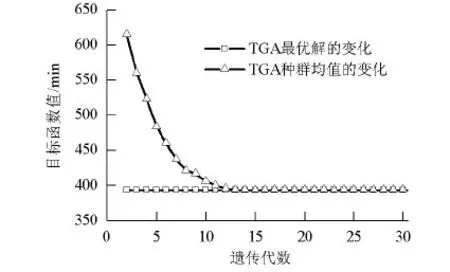
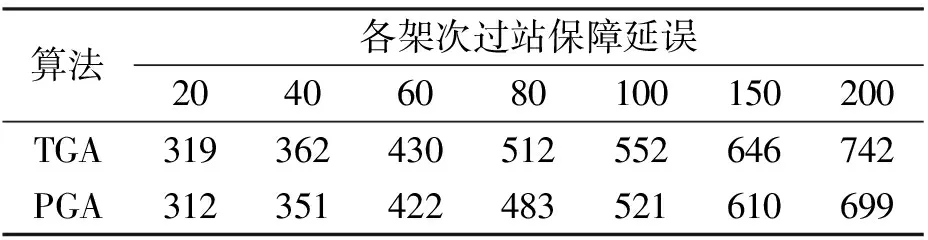
设在某时段内有n架飞机S={Si}(i=1,2,…,n)需开展过站保障,第i架飞机过站时段为[ti,0,ti,2]、需调度车辆完成的过站作业集r={rj}(j=1,2,…,k),第i架飞机的第j个保障作业记为Jij,Jij耗时为时间区间[t1,t2](0 (1) ti,e=max{tij}, (2) tvp-tivh+M(1-uivh)≥tij, (3) tij-td,ij≥ts,ij, (4) 式中:α,β,γ为转换系数,将时间转化为保障成本费用;ti,e为飞机Si过站保障实际结束时间;ti,1为飞机Si过站计划结束时间;若车辆h先完成Si的任务,紧接着完成Sv(v=1,2,…,n,v≠i)的任务,则uivh=1,否则uivh=0;tivh为车辆h从Si所在机位行驶至Sv所在机位的耗时;th为车辆h从停放区、客货区或加油区行驶至机位耗时;tij为Si的作业任务rj的实际完成时间;tvp为飞机Sv的保障作业rp(p=1,2,…,k,p≠j)实际开始时间;M为一个足够大的数;td,ij为飞机Si保障作业rj耗时;ts,ij为飞机Si保障作业rj计划开始时间.式(1)为过站保障车辆调度优化的目标函数; 式(2)为求得飞机最后一个保障作业完成时间;式(3)为保证车辆在飞机之间的作业时序关系得到满足;式(4)为保证单一作业的耗时需求得到满足. 表1 某机场飞机过站保障作业任务编号、时序约束、耗时及所需车辆类型Tab.1 Task code,temporal constraint,time consumption,and service vehicle for aircraft turnaround in one airport 注:“—”表示不需要车辆;“*”表示相应车辆仅在飞机停靠远机位时需要. 表2 某机场飞机过站保障车辆配备规则及车辆总量参照表Tab.2 Scheduling rules and total number of vehicle for aircraft turnaround service in one airport 采取两级递阶式染色体编码结构,如图2(a)所示.第1级为控制基因串g,各基因位可用需要调度车辆的作业任务编号表示;第2级为参数基因串c,各基因位是给第1级控制基因中对应任务指派的车辆编号.染色体分成若干片段,每一个片段对应一架飞机的过站保障车辆调度方案,其中:gi为飞机Si的作业任务编码,长度记为li1;ci为飞机Si的保障车辆编码,长度记为li2. 基于两种策略产生染色体编码:(1) 策略1:就近指派(minimum transition,MIN_T),即距离待保障飞机最近的车辆优先被调度;(2) 策略2:使用率均衡(average load,AVE_L),即尽可能保证同类车辆机会均等地被调度.对飞机Si,将需使用保障车辆的作业任务编号组成任务集Ti={Jij},任务Jij的可调度车辆编号组成集合,用B(Jij)表示.若3架飞机任务集分别为T1={1,2,3},T2={1,2,4},T3={1,3,4},车辆集为B(1)={1,2,3},B(2)={4,5,6},B(3)={7,8,9}.用所给编码方法基于AVE_H策略编码一个染色体,如图2(b)所示. 定义1作业Jij的前序作业集P(Jij)为满足飞机过站保障作业时序关系约束,将作业Jij开始之前必须完成的作业的集合定义为其前序作业集.P(Jij)=P(Jio)∪…∪P(Jis).其中,Jio,…,Jis为Jij的紧前作业,o,s∈{1,2,…,k} 定义2作业Jij的相容作业集O(Jij)为在满足过站保障作业时序关系和可用车辆资源约束下,允许与Jij同时展开的作业集合,定义为其相容作业集.Jij与Jiw为相容作业,也就是Jij与Jiw无作业时序关系约束,且Q(Jij)≤N(Rq),Q(Jiw)≤N(Rq). 步骤1对控制基因染色体片段gi的第z个基因位置,从任务集Ti中随机选取一个任务Jij,并依据表1求解该作业对应的前序作业集P(Jij),若P(Jij)中所有任务编号均已编入gi,则将Jij作为染色体片段gi中第z个基因位基因,同时,若任务Jij的相容作业集O(Jij)≠φ,则将O(Jij)中的所有任务编号也编入gi,转步骤2;否则,重新步骤1. 步骤2对参数基因染色体片段ci,依据步骤1 确定的任务Jij及车辆配备规则(见表2)确定任务Jij所需车辆数量Q(Jij);从车辆集B(Jij)中基于MIN_T策略或AVE_L策略随机选取Q(Jij)个不同的车辆编号,将其作为片段ci中连续Q(Jij)个基因位基因;同理,确定O(Jij)中各任务所需车辆总数量∂及相应车辆编号,进而确定染色体片段ci中连续∂个基因位基因;转步骤3. 步骤3若z 步骤4若i (b) 递阶式染色体编码示例图2 保障车辆调度的两级递阶式染色体编码结构及示例Fig.2 Two-level hierarchical chromosome coding structure for service vehicle scheduling and the coding example 定义3车辆可调度能力空间定义为车辆可供调度开展机位保障的时段[ts,te]的集合,记为Π. 染色体解码主要考虑基于作业时序关系约束,某个作业任务允许开始时,指派的保障车辆能否及时到达相应机位进而确定作业实际开展时段.基于车辆可调度能力空间概念的染色体解码算法如下: 步骤1对控制基因染色体片段gi,取其中第j个基因位gi(j),其实质代表某一作业任务. 步骤3对参数基因染色体片段ci,从其中取出为作业gi(j)指派的车辆编号集合φ(gi(j)). 步骤4对车辆h∈φ(gi(j)),取对应的可调度能力空间Πh中时长大于ρ的时段集合P;并确定车辆h由前一个保障任务所在机位行驶至当前任务机位的耗时ζ. 步骤5将集合P中各时段按起始时间由小至大排序,并取第一个时段[ts,te]. 步骤8同理,对φ(gi(j))中的其它车辆,复步骤4~7. 步骤9对控制基因染色体片段gi中的其他基因位,重复步骤1~8;否则,转步骤10. 步骤10若i 以图2(b)中前两架飞机任务1的染色体解码过程进行说明.图中:x1为随机迭足;x2为基因换位的掉作位置.假设车辆在机位间由停放区行驶至机位的耗时均为5 min,飞机过站时段分别为[5,68]和[12,82],保障任务1耗时为6 min,所有车辆初始可调度能力空间为{[0,200]}.对控制基因g1(1)={1}和参数基因c1(1)={1,2},由于车辆1需由停放区行驶至机位方可开展作业,故解码后飞机1的作业任务1的保障时段为[5,11],此时,车辆1、2的可调度能力空间分别更新为Π1={[11,200]}、Π2={[11,200]};对控制基因g2(1)={1}和参数基因c2(1)={1,3},由于车辆1完成任务g1(1)后行驶至飞机2所在机位的时刻为11+5=16>12,故调度车辆1完成作业任务g2(1)的时段为[16,22],车辆3开展飞机2的作业任务1的时段为[12,18];对应地,车辆1、3的可调度能力空间分别更新为Π1={[22,200]},Π3={[0,7],[18,200]}.同理,可完成染色体所有基因位的解码操作. 设计一种新的换位变异混合算子,具体做法为: 步骤1选择种群中任一染色体,其所含控制基因串和参数基因串分别为g、c. 步骤2随机选择对应飞机Si的控制基因染色体片段gi和参数基因染色体片段ci. 步骤3随机选取片段gi上基因位gi(x1)和gi(x2)并进行换位操作,若新生成的基因片段符合作业时序约束(见表1),则步骤4;否则,继续步骤3. 步骤4考虑递阶式染色体编码中下级基因受上级基因的控制,将参数基因片段中对应于控制基因位gi(x1)和gi(x2)的参数基因串ci(x1)和ci(x2)也进行换位操作,其中,x1、x2为随机选定的基因位. 步骤5对参数基因串c,随机选取两个参数基因片段ck和cy,将两个片段中分别对应于同一种作业任务的参数基因串ck(x3)和cy(x4)进行换位操作,其中,x3、x4为随机选定的基因位. 步骤6对种群中的所有染色体均重复步骤1~5. 步骤3~4对控制基因染色体片段采取段内换位变异(见图3(a)、(b)),以满足作业时序关系约束;步骤5对参数基因染色体片段采取段间换位变异(见图3(c)、(d)),以满足车辆指派规则约束. 机位保障过程中,飞机未在过站时段结束之前完成保障产生的惩罚费用和车辆行驶费用之和为 (5) 为简化问题,将式(5)中第3项纳入机位作业耗时.因此,本文单亲遗传算法的染色体适应值函数为 (6) 采用轮盘赌选择策略,并同时加入最优保持策略以保证算法的全局收敛性. 为验证算法有效性,对表3中过站飞机开展保障车辆调度优化.具体作业流程、车辆配备规则及可调度车辆信息见表1和表2.种群规模NNIND=30,遗传代数GGEN=30,换位变异概率NMUX=0.8.计算遗传算法适应度函数值时,α=1.00,β=0.02.采取MIN_T策略和AVE_L策略分别产生初始种群,相应调度优化结果分别如图4(a)、(b)所示,展示了每一保障车辆的具体作业时段. 表3 飞机过站信息Tab.3 Aircraft turnaround information 由图4可知: 在两种策略下,最后一道保障作业(即牵引车作业)完成时间相近,即过站保障造成的飞机延误水平较为接近;在就近指派策略下,同一车辆工作时段更为密集,意味着车辆行驶时间相对要少,更利于降低保障成本. (a)MIN_T策略(b)AVE_L策略图4 两种策略下的过站保障车辆作业时段甘特图Fig.4 Ganttchartforservicevehiclesoperationbasedontwovehicledispatchingstrategies 考虑不同架次并基于上述两种策略各运行50次,得到的结果见表4.由表4可知:针对不同保障架次,与AVE_L策略相比,MIN_T策略在过站保障延误方面平均改进4%,在车辆行驶时间方面平均改进40%,这与图4对比分析的结果是一致的;在遗传代数和计算耗时方面,不同架次下相差不大,表明本文算法可适用不同规模的问题求解.同时,现场采集的实际数据表明,与MIN_T和AVE_L策略相比,现场人工指派策略(current,CUR)在过站保障延误方面同它们均较为相近,而在车辆行驶时间方面,MIN_T策略较CUR策略平均改进11%,CUR策略较AVE_L平均改进30%.因此,为提高车辆的运行保障效益,可采用本文所给调度算法和MIN_T策略. 表4 不同调度策略下的过站保障车辆优化调度结果Tab.4 Optimized scheduling results based on different service vehicle scheduling strategies 将传统遗传算法(traditional genetic algorithm,TGA)与本文单亲遗传算法(partheno genetic algorithm,PGA)进行比较.两种算法种群规模30,遗传代数30,染色体编码和解码方式相同.TGA的交叉和变异概率通过反复试验试凑确定,其中在交叉概率为0.7,变异概率为0.2时,TGA解决该问题的收敛速度较快.结果表明,两种算法在不同架次下均能较快收敛.采取两种算法并基于MIN_T策略的种群最优解和均值变化趋势如图5、6. 图5 传统遗传算法优化性能Fig.5 Convergence effect of Traditional Genetic Algorithm 图6 本文单亲遗传算法优化性能Fig.6 Convergence effect of partheno-genetic algorithm 由图5可知,本文所给PGA收敛速度优于TGA.表5给出了不同架次下采用两种算法开展调度的过站保障延误情况.由表5可知,在架次较少时,TGA与PGA所得结果较接近,但随着架次增多,PGA明显优于TGA. 表5 不同过站飞机架次下的车辆调度TGA和PGA结果比较Tab.5 Scheduling results comparison between TGA and PGA for different numbers of turnaround aircraft min (1) 递阶式染色体编码综合考虑保障作业任务时序约束和车辆指派规则约束,可直观描述保障车辆调度过程;(2) 换位变异算子采取控制基因染色体片段段内换位变异和参数基因染色体片段段间换位变异相结合的方式,避免了非法染色体产生,可有效压缩寻优空间,提高求解效率;(3) 提出保障车辆可调度能力空间概念并设计相应解码算法,保障解码结果的可用性.所给算法对过站保障车辆集中式调度有效.今后可考虑飞机过站时段不确定性和作业任务耗时的动态性来研究保障车辆调度优化问题. 参考文献: [1]丁建立,赵键涛,曹卫东.基于贝叶斯网的航班过站时间动态估计[J].南京航空航天大学学报,2015,47(4):517-524. DING Jianli,ZHAO Jiantao,CAO Weidong.Dynamic estimtion about turnaround time of flight based on Bayesian network[J].Journal of Nanjing University of Aeronautics and Astronautics,2015,47(4):517-524. [2]VIDOSAVLJEVIC A,TOSIC V.Modeling of turnaround process using Petri Nets[C]∥Proc.of the 14th ATRS World Conference.Porto:EUROCONTROL,2010:1-13. [3]MIQUEL A,ALEXEY N,CESAR T.A simulation model to improve air cargo operations in passenger aircraft[C]∥Proc.of the 2010 Summer Computer Simulation Conference.San Diego:IEEE Press,2010:446-451. [4]FRANCISCO F,MIQUEL E,JENARO N.Use of colored petri nets to model aircraft turnaround at an airport[C]∥Proc.of the 6th International Conference on Scientific Computing to Computational Engineering.Athens:[s.n.], 2014:1-8. [5]孙瑞山,张子仝.基于CPM停机坪航班保障工作方法研究[J].中国民航大学学报,2011,29(5):23-29. SUN Ruishan,ZHANG Zitong.Study on apron flight service work method based on CPM[J].Journal of Civil Aviation University of China,2011,29(5):23-29. [6]NORIN A,GRANBERG A G,YUAN D,et al.Airport logistics-a case study of the turn-around process[J].Journal of Air Transport Management,2012,20(3):31-34. [7]DU J Y,BRUNNER J O,KOLISCH R.Planning towing processes at airport more efficiently[J].Transportation Research Part E,2014,70(1):293-304. [8]CHEUNG A,LP W H,LU D.An aircraft service scheduling model using genetic algorithms[J].Journal of Manufacturing Technology Management,2005,16(1):109-119. [9]YUQUAN D,QIAN Z.ACO-IH:An improved ant colony optimization algorithm for airport ground service scheduling[C]∥Proc.of IEEE International Conference on Industrial Technology.Chengdu:[s.n.],2008:1-6. [10]姚韵,朱金福,柏明国.航班过站地面服务的优化调度算法[J].信息与控制,2007,36(4):486-492. YAO Yun,ZHU Jinfu,BAI Mingguo.An optimization scheduling algorithm for flight turnaround ground service[J].Information and Control,2007,36(4):486-492. [11]苟晶晶.机场规划所需地勤保障车辆最低数量预测[J].中国民航飞行学院学报,2015,27(2):50-53. GOU Jingjing.Prediction of the minimum requirement of ground vehicles for airport planning[J].Journal of Civil Aviation Flight University of China,2015,27(2):50-53. [12]王芹,樊玮.飞机地面作业提前/拖期调度研究[J].计算机工程与应用,2008,44(10):214-216. WANG Qin,FAN Wei.Research on earliness/tardiness scheduling about airplane ground job operation[J].Computer Engineering and Applications,2008,44(10):214-216. [13]樊琳琳.大型机场地勤服务中的车辆调度问题的初步研究[D].沈阳:东北大学,2009. [14]VAN LEEUWEN P,LEN OEI L,BUZING P.Adaptive temporal planning at airports[R ].Amsterdam:National Aerospace Laboratory NLR,2007. [15]VAN LEEUWEN P,WITTEVEEN C.Temproal decoupling and determining resource needs of autonomous agents in the airport turnaround process[R].Amsterdam:National Aerospace Laboratory NLR,2009.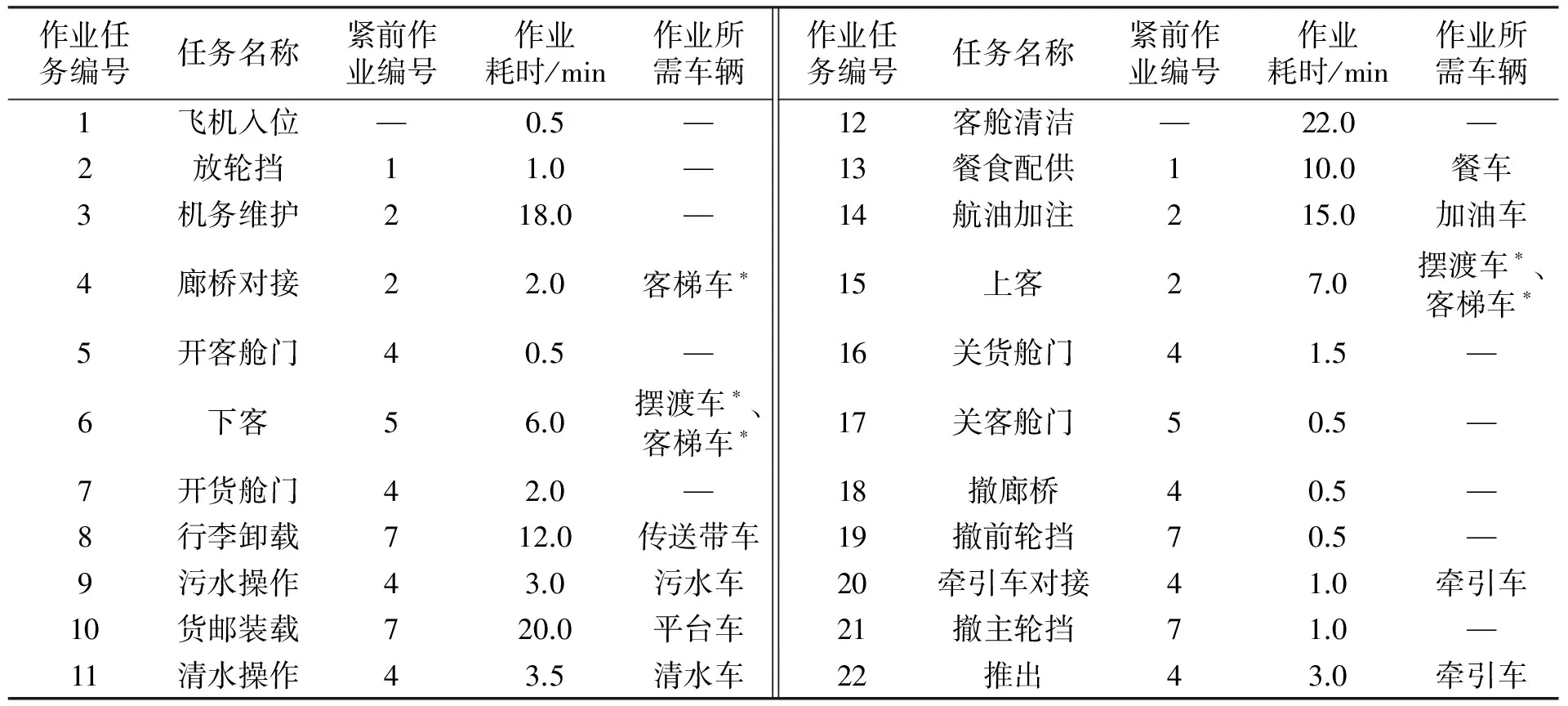
2 递阶式编码结构单亲遗传算法
2.1 染色体编码
2.2 种群初始化
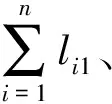

2.3 染色体解码

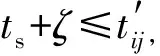

2.4 换位变异算子设计
2.5 适应度函数
2.6 选择算子
3 算法验证



4 结 论
