砂土地层盾构隧道稳定性三维离散元研究
2018-04-11林国进
王 俊,林国进,唐 协,何 川
(1.西南交通大学交通隧道工程教育部重点实验室,四川 成都 610031; 2.四川省交通运输厅公路规划勘察设计研究院,四川 成都 610041)
砂土地层是我国城市盾构隧道建设中遇到的一种典型地质条件,具有离散性强、黏聚力弱等特点,对外界扰动反应灵敏.盾构在该类介质中掘进时若支护压力不足可能诱发掌子面坍塌,给国民经济造成重大损失.因此开展砂土地层盾构掘进掌子面的稳定性研究是十分必要的.
目前,采用理论分析、模型试验以及数值模拟等方法对盾构隧道掌子面稳定性进行了研究.理论分析包括极限平衡理论与极限分析理论,前者需预先假定失稳区大小与形状,如对数螺旋曲线[1]、半球体和半圆[2]、楔形体[3-5]等.后者则需要假设应力场分布[6-8](下限解)或者速度场分布[8-9](上限解).
模型试验主要通过应力[10]或应变[11-13]的控制方式研究隧道掌子面稳定性.Chambon和Corté[10]通过逐步减小支护压力并结合地层变形情况得到掌子面极限支护压力;Kirsch与Idinger等[11-12]则通过后撤挡板模拟盾构开挖,同时监控作用在挡板上的土压力,并根据开挖状态将其视为极限或者残余支护压力.
随着计算机技术的不断发展,数值模拟在隧道掌子面稳定性研究中得到了广泛运用.有限元方面,Vermeer等[14]认为排水条件下极限支护压力随内摩擦角的增大而减小;Li等[15]采用FLAC3D研究了软土地层大直径泥水盾构掘进掌子面稳定性问题.离散元方面[16-20],王俊等[17]采用PFC2D研究了砂卵石地层中泥水盾构掌子面稳定性;Chen等[19]通过后侧挡板模拟了砂土地层盾构隧道掌子面失稳.
上述研究虽取得诸多成果,但仍有一定不足:如理论分析主要适用于简单本构土体,一般不考虑土拱效应与隧道开挖过程的影响;模型试验能从宏观上把握掌子面失稳现象,但限于观测手段难以解释失稳机理且不易开展参数研究;数值模拟主要采用有限元方法开展,计算结果受本构模型选取、网格划分精度等因素影响较大,且在模拟土体大变形问题上存在困难.既有的三维离散元研究也存在局限性:如Chen等[19]采用的研究方法难以模拟隧道开挖过程,且不能直接得到掌子面极限支护压力;Melis Maynar和Medina Rodrigue[20]则采用地层黏聚力评价掌子面稳定性,研究成果不能用于砂土地层.
鉴于此,本研究以Chambon和Corté[10]开展的室内模型试验为基础,采用三维离散元方法建立了与之相匹配的数值模型,从细观角度解释了砂土中盾构隧道开挖面失稳机理,研究了极限支护压力、失稳区分布、土拱效应和地层移动规律.数值模型中引入了三维动态柔性应力边界,该应力边界可有效模拟室内试验中仓内介质(空气、流体)对开挖面的支撑效应,将其抽象为作用在掌子面颗粒上的指定支护压力,模拟过程中分步等量减小该压力直到隧道失稳.与既有研究相比,本文通过删除进入隧道内部的土颗粒模拟隧道开挖,考虑了该施工行为对掌子面稳定性的影响,采用的三维柔性应力边界可精确得到极限支护压力.
1 三维动态柔性应力边界
1.1 室内试验简介
Chambon与Corté[10]开展的模型试验如图1所示.模型箱尺寸为1.20 m(长)×0.80 m(宽)×0.36 m(高),采用Fontainebleau砂进行试验,主要物理力学性质为:颗粒平均粒径d50=0.17 mm;不均匀系数Cu=1.47;重度为15.3~16.1 kN/m3;内摩擦角为38°~42°;黏聚力为0~5 kPa.采用静水压力或空气压力模拟试验中掌子面处的支护压力,考虑了C/D=0.5,1.0,2.0,4.0 等4种埋深工况,其中:C为隧道埋深,D=0.1 m 为隧道直径.试验考虑了50g、100g和130g3种加速度情况,对应的原型隧道直径分别为5、10 m 和 13 m.
室内试验中首先将掌子面处的支护压力设为隧道轴线处的主动土压力,此后逐步减少该压力,模拟隧道失稳结合地层变形情况得到极限支护压力与失稳区分布.
1.2 三维动态柔性边界算法
采用三维离散元方法PFC3D建立Chambon和Corté室内试验数值模型的主要难点是如何描述模型试验中静水压力或空气压力对掌子面的支护效应.由于水和空气均是流动性较强的介质,不能承受剪切力,故其对隧道的支护效应可视为作用在掌子面上的法向力,仓内介质与开挖面的相互作用可简化为三维应力边界问题,且该应力边界随隧道掌子面处土体位移变形而不断演化.

图1 Chambon和Corté室内模型试验Fig.1 Sketch of Chambon and Corté’s model test
为在PFC3D模型中构建该应力边界,通过内置Fish语言[21]进行编程将仓内介质对掌子面的支护效应抽象成作用在掌子面颗粒上的指定法向压力.如图2(a)所示,程序实现的基本思想是假设在盾构正后方存在一个边长与盾构直径相等的平面,并对其进行离散化处理,得到一系列晶格,所有的颗粒均沿隧道轴线向离散晶格投影,得到该方向上距对应晶格最近的所有颗粒(即掌子面颗粒),再根据颗粒在对应晶格上的投影面积Ap(图2(b))给掌子面颗粒施加指定的支护力f=pAp(p为仓内支护压力,kPa),便实现了给掌子面施加支护,构建了仓内介质与掌子面土体之间相互作用的应力边界.为了便于理解,可以将晶格视作向掌子面发射平行光的光源,所有能接收光照的颗粒就是掌子面颗粒,其所受的支护力与光照面积成正比.
划分晶格时需注意砂土颗粒平均直径(davg)与晶格尺寸(l)之间的大小关系,davg/l过小则计算误差大,过大则计算耗时,经过多次试算最终选取davg/l=16.掌子面颗粒与离散晶格的相对关系如图3所示.
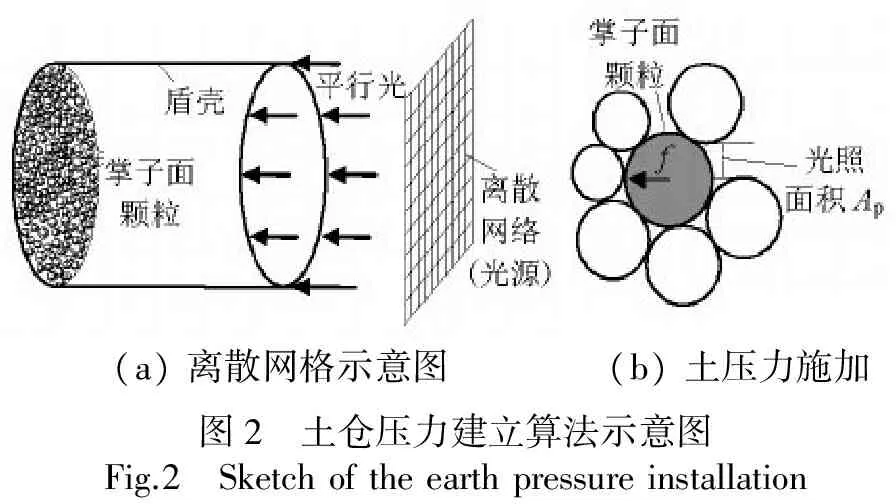
(a)离散网格示意图(b)土压力施加图2 土仓压力建立算法示意图Fig.2 Sketchoftheearthpressureinstallation

图3 掌子面颗粒与离散晶格相对关系Fig.3 Relationship between grid cell and sand particle
2 三维离散元数值模型
2.1 细观参数标定
采用三轴试验对模型中采用的砂土颗粒进行了标定.考虑到隧道埋深,标定围压σ3选为50、100、200 kPa.最终选用的细观力学参数如表1所示,标定后的宏观力学参数内摩擦角φ=38°,黏聚力c=0 kPa,与室内模型试验采用的Fontainebleau砂的物理力学性质基本一致.1#材料标定过程的应力应变曲线如图4所示.

表1 PFC3D细观力学参数Tab.1 Calibrated PFC3D microscopic parameters

图4 材料细观参数标定Fig.4 Calibration of microscopic parameters
本次三轴试验对传统标定方法进行了改进,采用前述三维柔性应力边界代替刚性wall单元构建了侧向约束,有效模拟了室内试验中橡皮膜对试样的柔性包裹.如图5(a)所示,假设在试样周围存在两个正交平面,并对其进行离散化处理,得到一系列晶格.所有土颗粒均沿x和z方向向晶格i(1≤i≤n,n为晶格总数)投影,得到距离晶格i最近和最远的颗粒.当确定了距任意晶格最远和最近的土颗粒便得到了试样中的边界颗粒.作用在边界颗粒上的力则为指定围压与颗粒横截面积的乘积,再根据颗粒形心坐标与试样中心的夹角将该力沿x与z方向进行分解并施加在对应颗粒上,便实现给所有边界颗粒施加相等的径向压力.随着试样不断加载,边界颗粒的位置会发生变化,数值三轴试验中每隔100步执行一次三维柔性应力边界算法,更新边界颗粒并调整作用在其上的围压.
最终剪切破坏的试样如图5(b)所示.
为提高计算效率,在隧道轴线范围内的地层由1#土颗粒构成,其余范围内的地层由2#土颗粒组成,两种颗粒均采用线性接触模型,颗粒粒径服从 0~1均匀分布.
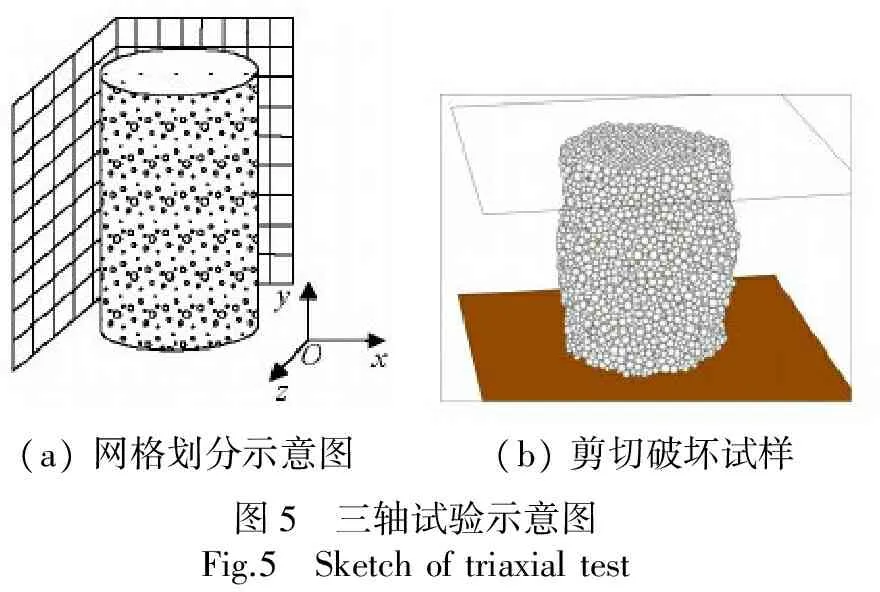
(a)网格划分示意图(b)剪切破坏试样图5 三轴试验示意图Fig.5 Sketchoftriaxialtest
2.2 PFC3D数值模型
如图6所示,综合考虑边界效应与计算效率,数值模型尺寸为:长(L)×宽(B)=18 m×25 m,高度(H)由隧道埋深确定,共考虑了C/D=0.5、1.0、2.0、4.0 4种埋深工况,隧道直径D=5.0 m.隧道轴线上下方各3.5 m范围内(粒径满足8~12cm的颗粒分布范围m=7.0 m)的砂土颗粒粒径分布为8~12 cm,其余部位为15~20 cm.盾构埋入地层中的长度S1为7.0 m,地层外的长度S2为2.5 m,隧道下方土体厚度W为4 m.为了得到隧道失稳过程中地层变形情况,模型中布设了如图6所示的位移测点.
数值模拟按以下步骤进行:
步骤1采用wall单元生成地层模型边界后(wall单元法向与切向刚度均为1×108N/m,摩擦因数为0),根据标定的细观参数,采用“落雨法”分层生成地层模型,在重力作用下完成固结后删除地层顶部少量浮皮颗粒;
步骤2在指定范围内(y≤0,x2+z2≤2.52)删除地层颗粒并采用wall单元生成盾构机,其法向与切向刚度均为1×1011N/m,摩擦因数为0.2;
步骤3利用三维动态柔性边界算法识别掌子面颗粒,并施加与隧道轴线处静止土压力相等的初始支护压力,此后分步等量减少该支护压力直至0 kPa,同时密切监控掌子面前方土体位移变化,当测点位移突然增大时,可以认为此时的支护压力为掌子面极限支护压力[10].

(a)纵剖面(b)纵剖面图6 模型尺寸与测点布置示意图Fig.6 Sketchofmodelandmonitoringpointdistribution
为提高计算精确度,每一级支护压力下均迭代50 000步,保证模型达到平衡状态.C/D=2.0时的数值模型见图7.
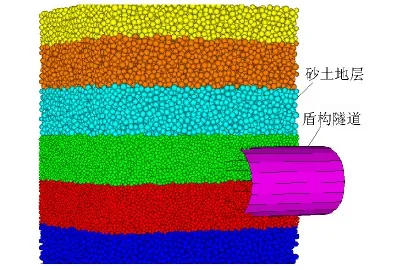
图7 PFC3D数值模型Fig.7 PFC3D numerical model
3 数值模拟结果分析与讨论
通过分析数值计算结果中地层变形以及土体应力场数据,得到了掌子面极限支护力、掌子面失稳破坏模式、地层移动与掌子面附近土体应力变化规律.本文主要介绍开挖面极限支护力、失稳区范围与开挖面前方土拱效应发展规律等.
3.1 数值模型合理性验证
将数值计算结果与室内模型试验相对比验证其合理性.为了得到极限支护压力,在减小支护压力的同时密切记录地层变形情况,得到两者之间的关系曲线.限于篇幅本文只给出了C/D=2.0时地中测点位移随支护压力减小变化情况(图8).该测点位于隧道拱顶正前方1.0 m,坐标为(0.0,1.0,2.5),由文献[10-12]知,该点位于失稳区中心位置,能及时反应隧道失稳.

图8 地中测点沉降与支护压力关系曲线Fig.8 Relationship between subsurface settlement and support pressure
从图8可以看出,测点位移随支护压力p变化曲线可以分为两个阶段:初始阶段测点位移随p减小逐渐增大,但变化幅度很小;当p减小到特定值时,测点位移突然快速增大,由文献[10]可判定p为极限支护压力(pf).按此办法,本研究给出了所有工况的掌子面极限支护压力,具体结果如表2所示.

表2 不同埋深条件下掌子面极限支护压力Tab.2 Limit support pressure under various C/D
如图9所示,引入无量纲系数pf/(γD)将离散元计算与Chambon和Corté[10]模型试验结果进行了比较,γ为土体重度.
由图9可知,两种研究中极限支护压力随隧道埋深变化规律是相同的,可以分为两个阶段:C/D≤1.0时极限支护压力随C/D增长较快,而当C/D≥2.0时极限支护压力趋于稳定,基本不随埋深变化而变化.但数值计算得到的结果绝对值大于模型试验,出现该结果的可能原因是Chambon和Corté[10]离心试验采用的砂土物理力学性质具有一定的不确定性,内摩擦角在38°~42°范围内变化大于数值模型中砂土的内摩擦角(φ=38°),还可能具有一定的黏聚力(0≤c≤5 kPa),而数值模型中砂土黏聚力为0.由Vermeer等[14]的研究可知掌子面极限支护压力随砂土地层的内摩擦角减小而增大,此外由文献[7-9]知,黏聚力可以有效提高地层自稳性,减小极限支护压力,故数值计算与模型试验之间的差异是合理的.

图9 数值计算结果与其他研究比较Fig.9 Comparison between numerical results and other researchs
此外,将离散元计算结果与理论研究[4,8-9]和Kirsch模型试验[11]结果也进行了对比.离散元计算结果略大于Leca和Dormieux[8]与Mollon等[9]给出的上限解,由极限分析中上限解的定义知该结论是合理的;离散元计算结果与Anagnostou和Kovari[4]提出的三维楔形体模型吻合良好,当C/D≤1.0时两者结果基本相同,当C/D=2.0时前者略小于后者,出现该现象的可能原因是当C/D≥2.0时隧道拱顶上方出现土拱效应,提高了隧道的自稳能力,而楔形体模型中由于没有考虑该效应,掌子面极限支护压力大于数值计算结果,关于土拱效应的具体分析可见3.5小节.Kirsch[11]模型试验中采用的砂土摩擦角为32.5°,小于本模型中的38.0°,Vermeer等[14]认为掌子面极限支护压力随砂土地层的内摩擦角减小而增大,故离散元结果小于该模型试验也是合理的.综上所述,研究采用的数值模型是合理可行的.
定义支护压力比η=p/p0,其中,p0为初始状态隧道轴线处静止土压力,则4种工况下极限支护压力比ηf分别为12.0%、11.7%、9.6%、5.8%,ηf随C/D的增加而减小.
3.2 失稳区分布
明确失稳区形状与大小分布是掌子面稳定性研究中的重点,特别是在极限平衡理论分析中.本文通过以下两个步骤得到失稳区分布:
步骤1记录图6中所有测点的竖向位移;
步骤2根据同一断面处测点位移梯度判定失稳区范围,依次连线所有位移突增点得到失稳区分布.
图10给出了隧道失稳时典型断面处(C/D=2.0,y=0.5,z=3.0)测点位移分布情况.
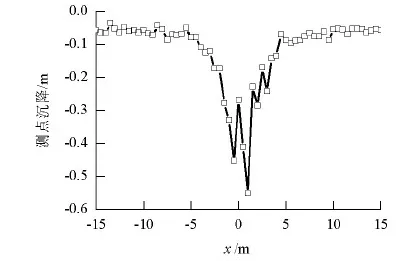
图10 典型横断面上地层变形情况Fig.10 Typical vertical displacement curve at transverse profile
如图11所示,采用上述办法给出了4种埋深工况下隧道失稳区分布形态.
由图11可知,对C/D=0.5来讲,p=pf,0 kPa时失稳区均呈烟囱状,且发展到地表,数值计算得到的分布范围略大于模型试验,出现该现象的可能原因是模型试验中砂土内摩擦角大于数值模型,且可能存在一定的黏聚力.
计算结果表明:失稳区从拱底开始向上发展,p=pf时发展至掌子面前方约0.77D处,p=0 kPa时发展至1.02D,此外失稳区从拱顶处还向隧道后方延伸一定范围;C/D=1.0时,失稳区同样发展至地表,与模型试验结果不同,具体形态与C/D=0.5基本相同,但分布范围更大;C/D=2.0,4.0时,失稳区没有发展到地表,分布范围略大于模型试验,两种埋深条件下失稳区均在拱顶后方有一定范围的延伸.
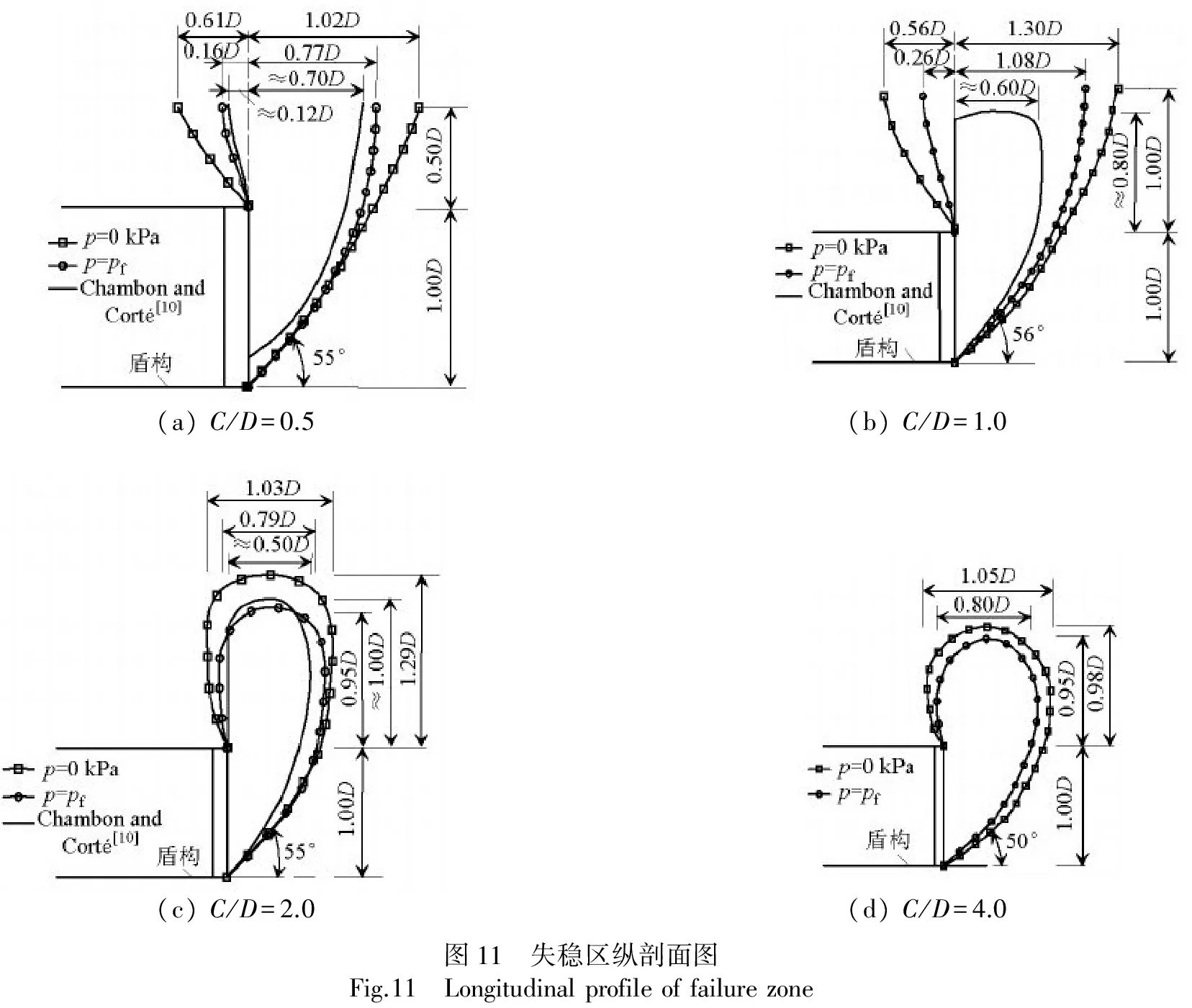
(a)C/D=0.5(b)C/D=1.0(c)C/D=2.0(d)C/D=4.0图11 失稳区纵剖面图Fig.11 Longitudinalprofileoffailurezone
3.3 地表沉降
图12给出了C/D=2.0时地表典型测点(坐标为(0.0,1.0,12.5))沉降随支护压力变化曲线.
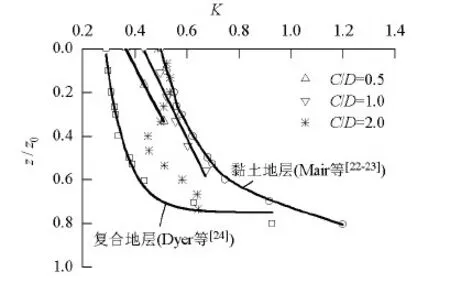
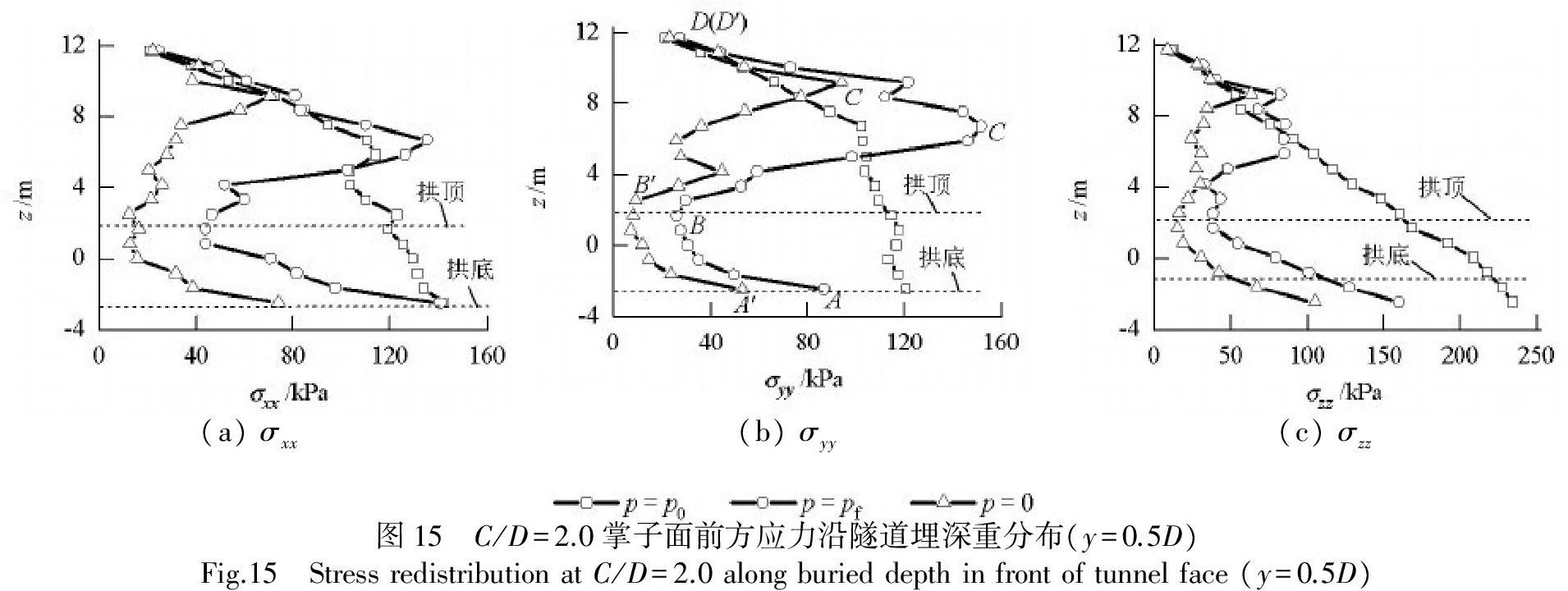
由图12可知,相比于地中测点,地表测点沉降具有滞后性,地表沉降突增点对应的支护压力pk 图12 地表测点沉降与支护压力关系曲线Fig.12 Relationship between surface settlement and support pressure 为了整体把握地表沉降情况,给出了4种工况下沉降三维曲面.如图13所示,地表沉降范围随埋深增大而增大,最大沉降均出现在开挖面前方约0.16D(y=0.8 m)处,且其绝对值随埋深增大减小. 表3 不同埋深条件下地表位移突增时的支护压力Tab.3 pk under various C/D 由图13(a)可知:由于隧道埋深较浅,当C/D=0.5时,失稳区基本呈烟囱状发展至地表,地表沉降主要集中在隧道轴线两侧各4 m (0.8D)以及前方5 m (1.0D)范围内,同时向开挖面后方发展了大约2 m (0.4D),最大沉降达到了5.85 m;C/D=1.0时,地表沉降分布范围集中在轴线两侧各5 m (1.0D)以及前方6 m (1.2D)范围内,同时向隧道开挖面后方发展了大约3 m (0.6D),地表最大沉降为2.42 m;C/D=2.0时,地表沉降形态与C/D=1.0比较相似,但沉降区范围更广,地表最大沉降为0.41 m;C/D=4.0时,地表没有出现明显的规律. (a)C/D=0.5(b)C/D=1.0(c)C/D=2.0(d)C/D=4.0图13 地表沉降等高线图Fig.13 Surfacesettlementcontour 采用地中沉降槽宽度参数K研究了不同埋深条件下地中沉降情况,K=i/(z0-z),其中:i为沉降槽宽度系数;z和z0分别为地中某一水平面与隧道中心距离地表的高度. 图14为地中沉降槽宽度参数随深度比的变化情况,由图14可知:砂土地层的地中沉降槽宽度参数随深度比的变化规律与既有针对黏土和复合地层的研究结果差别较大,随着深度比的增大,C/D=0.5,1.0时地中沉降槽宽度参数基本呈线性增加,相同深度比条件下,C/D=0.5的地中沉降槽宽度参数要小于C/D=1.0,且两种地层的地中沉降槽宽度参数均大于复合地层地中沉降槽宽度参数,同时又都小于黏土地层地中沉降槽宽度参数;C/D=2.0时,可能由于拱效应,沉降槽宽度参数变化没有明显规律,但仍基本处于复合地层与黏土地层的包络线内. 图14 地中沉降槽宽度参数随深度比的变化Fig.14 Width parameter of subsurface settlement trough versus buried depth ratio 当C/D=2.0,4.0时,在掌子面上前方出现了土拱效应,有效地提高了隧道稳定性.为了定量解释该现象,图15、16中给出了两种工况下隧道掌子面前方0.5D处p=p0,pf,0 kPa时,垂直隧道轴线方向水平应力σxx、沿隧道轴向方向水平应力σyy、竖向应力σzz沿隧道埋深分布情况. 由图15可知,C/D=2.0时,应力分布沿埋深方向大致分为3个阶段.以σyy为例:(1) 由于隧道开挖,从隧道拱底(A点)至隧道拱顶(B点)应力释放明显,轮廓范围内应力不同程度减小;(2) 从拱顶至隧道上方一定范围内应力逐渐增加,并在拱顶上方约 4 m处达到极值;(3) 从C点至地表应力逐渐降为0. (a)σxx(b)σyy(c)σzz图15 C/D=2.0掌子面前方应力沿隧道埋深重分布(y=0.5D)Fig.15 StressredistributionatC/D=2.0alongburieddepthinfrontoftunnelface(y=0.5D) (a)σxx(b)σyy(c)σzz图16 C/D=4.0掌子面前方应力沿隧道埋深重分布(y=0.5D)Fig.16 StressredistributionatC/D=4.0alongburieddepthinfrontoftunnelface(y=0.5D) 由Chen等[13]研究可知,可通过定义水平应力集中系数λ判定土拱分布范围,λ=σ/σ0,其中:σ为任意时刻土压力;σ0为初始土压力.由于卸载效应,拱顶上方失稳区内有λ<1.0,而土拱将承担失稳区与两侧土体转移来的荷载,故有λ>1.0. 由图15可知:p=pf时土拱存在于拱顶上方约0.7D~1.3D范围内;当p从pf降至0 kPa时,土拱有向地表发展的趋势,与Chen等[13]室内试验结果基本吻合. 由图16可知:对C/D=4.0工况来讲,p=pf时主应力沿深度变化规律与C/D=2.0工况基本一致,塌落拱出现在隧道上方约0.9D~2.3D范围内;p降至 0 kPa后,土拱仍然向地表发展了一段距离. 以Chambon和Corté室内试验为背景,采用PFC3D开展离散元数值模拟从细观角度解释了砂土地层盾构隧道失稳机理.通过与理论分析和室内试验进行对比验证了数值模型的合理性.主要结论如下: (1) 掌子面极限支护压力pf与隧道埋深相关,C/D≤1.0时,极限支护压力随C/D增长较快;C/D≥2.0时,极限支护压力趋于稳定,基本不随埋深变化.极限支护压力比随埋深增加而减少. (2) 数值计算得到的失稳区分布范围稍大于模型试验,且失稳区均向隧道后方发展一段距离.C/D=0.5,1.0时,掌子面失稳向上发展引起地表坍塌;C/D=2.0,4.0时,在拱顶上方形成了稳定的塌落拱,塌落拱高度分别约为0.7D~1.3D与0.9D~2.3D. (3) 地表沉降突增点对应的支护压力pk (4) 隧道埋深越浅,地表沉降范围越小,最大沉降值越大,最大地表沉降出现在掌子面前方0.16D处.C/D=0.5,1.0时砂土地层的地中沉降槽宽度参数大于复合地层但小于黏土地层,且随埋深比增加线性增长. 致谢:2014年度西南交通大学博士研究生创新基金;第四届西南交通大学轨道交通行业拔尖创新人才培育项目. 参考文献: [1]MURAYAMA S,ENDO M,HASHIBA T,et al.Geotechnical aspects for the excavating performance of the shield machines[C]∥The 21st Annual Lecture in Meeting of Japan Society of Civil Engineers.Tokyo:[s.n.],1966:134-140. [2]KRAUSE T.Schildvortrieb mit flüsigkeits-und erdgestüzter ortsbrust[D].Brunswick:Technical University Carolo Wilhelmina,1987. [3]HORN N.Horizontal earth pressure on the vertical surfaces of the tunnel tubes[C]∥National Conference of the Hungarian Civil Engineering Industry.Budapest:[s.n],1961:7-16. [5]BROERE W.Tunnel face stability and new CPT application[D].Delft:Delft University,2001. [6]ATKINSON J H,POTTS D M.Stability of a shallow circular tunnel in cohesionless soil[J].Geotechnique,1977,27(2):203-215. [7]DAVIS E H,GUNN M J,MAIR F R,et al.The stability of shallow tunnels and underground openings in cohesive material[J].Geotechnique,1980,30(4):397-416. [8]LECA E,DORMIEUX L.Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J].Geotechnique,1990,40(4):581-606. [9]MOLLON G,DIAS D,SOUBRA A H.Face stability analysis of circular tunnels driven by a pressurized shield[J].Journal of Geotechnical and Geoenvironmental Engineering,2010,136(1):215-229. [10]CHAMBON P,CORTÉ J F.Sallow tunnels in cohesionless soil:stability of tunnel face[J].Journal of Geotechnical Engineering,1994,120(7):1148-1164. [11]KIRSCH A.Experimental investigation of the face stability of shallow tunnels in sand[J].Acta Geotechnica,2010,5(1):43-62. [12]IDINGER G,AKLIK P,WU W,et al.Centrifuge model test on the face stability of shallow tunnel[J].Acta Geotechnica,2011,6(2):43-62. [13]CHEN R P,LI J,KONG L G,et al.Experimental study on face stability of shield tunnel in sand[J].Tunnelling and Underground Space Technology,2013,33(1):12-21. [14]VERMEER P A,RUSE N M,MARCHER T.Tunnel heading stability in drained ground[J].Felsbau,2002,20(6):8-18. [15]LI Y,EMERIAULTB F,KASTNERB R,et al.Stability analysis of large slurry shield-driven tunnel in soft clay[J].Tunnelling and Underground Space Technology,2009,24(4):472-481. [16]CUNDALL P A,STRACK O D.A discrete numerical model for granular assemblies[J].Géechnique,1979,29(1):47-65. [17]王俊,何川,封坤,等.砂卵石地层中大断面泥水盾构泥膜形态研究[J].现代隧道技术,2014,51(6):108-113. WANG Jun,HE Chuan,FENG Kun,et al.Research on the dynamic behavior of the slurry membrane of a large-section slurry shield in a sandy cobble stratum[J].Modern Tunnelling Technology,2014,51(6):108-113. [18]缪林昌,王正兴,石文博.砂土盾构隧道掘进开挖面稳定理论与颗粒流模拟研究[J].岩土工程学报,2015,37(1):98-104. MIU Lingchang,WANG Zhengxing,SHI Wenbo.Theoretical and numerical simulations of face stability around shield tunnels in sand[J].Chinese Journal of Geotechnical Engineering,2015,37(1):98-104. [19]CHEN R P,TANG L J,LING D S,et al.Face stability analysis of shallow shield tunnels in dry sandy ground using the discrete element method[J].Computers and Geotechnics,2011,38(2):187-195. [20]MELIS MAYNAR M J,MEDINA RODRIGUEZ L E.Discrete numerical model for analysis of earth pressure balance tunnel excavation[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(10):1234-1242. [21]Itasca Consulting Group Inc.PFC3D (particle flow code in three dimensions) version 4.0 manual[M].Minneapolis:Itasca Consulting Group Inc,2001:101-235. [22]MAIR R J,TAYLOR R N,BRACEGIRDLE A.Subsurface settlement profiles above tunnels in clays[J].Gétechnique,1993,43(2):315-320. [23]MAIR R J.Centrifugal modeling of tunnel construction insoft clay[D].Cambridge:University of Cambridge,1979. [24]DYER M R,HUTCHINSON M T,EVANS N.Sudden valley sewer:a case history[C]∥International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground.London:[s.n.],1996:671-676.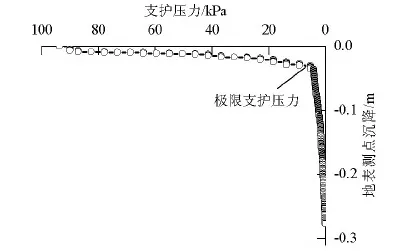


3.4 地中沉降
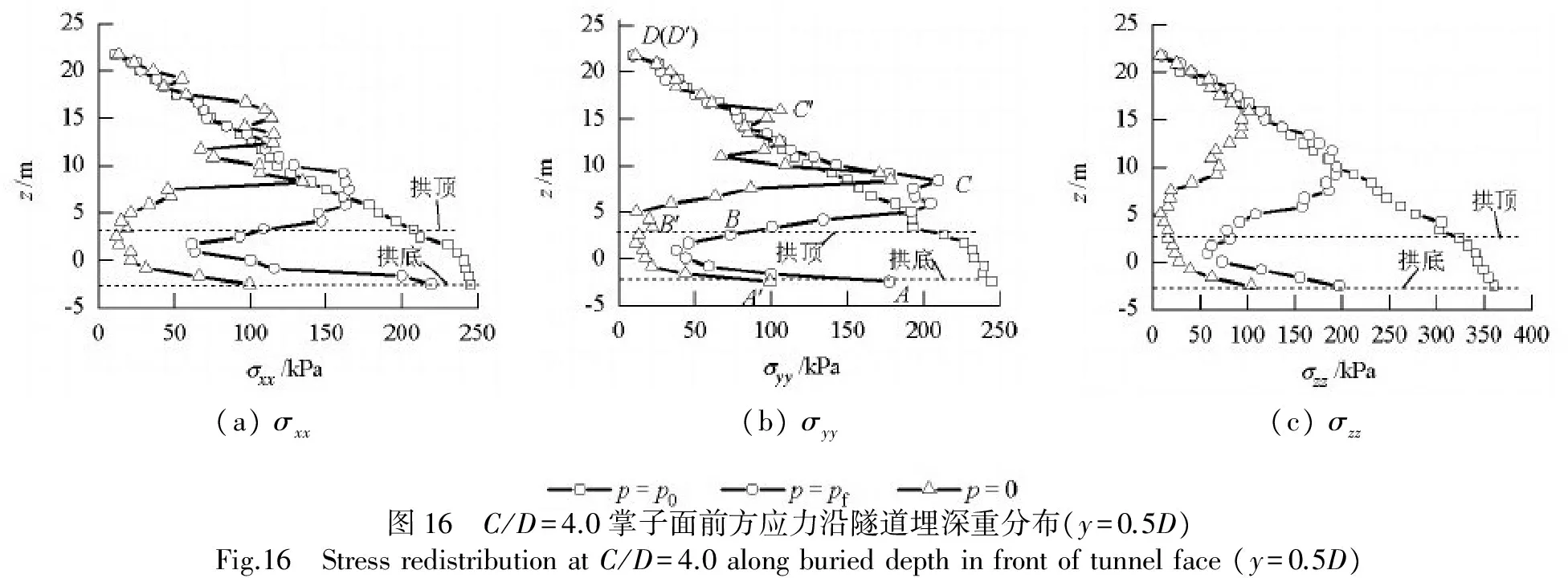
3.5 土拱效应分析
4 结 论
