考虑冻胀效应的冻结壁弹塑性分析

伏圣岗 ，冯　强 ，王成祥

(1.山东省土木工程防灾减灾重点实验室，山东 青岛 266590；2.山东科技大学 土木工程与建筑学院，山东 青岛 266590)

0　引　言

冻结法的原理是利用制冷系统吸收周围土体的热量使地层冻结，从而形成一个近似于圆筒状的冻结壁，使井筒与地下水断绝联系，让其在一个相对稳定干燥的地层中进行施工，这种施工方式得以在煤矿立井凿井、地铁施工以及基坑开挖等工程中广泛应用[1-2]。在冻结法施工中，冻结壁的设计是一个重要课题，许多学者通过试验方法从不同的角度来研究，例如：石荣剑等针对人工冻结法地铁施工出现的问题，依据相似理论设计冻结加固模型试验去研究形成预定厚度的冻结壁时所需要的冻结时间[3]；此外Ma等基于立井凿井的施工过程，分析了人工冻结土的强度与变形，实验结果表明人工冻结土在加载和卸载两种应力路径下的屈服强度差异很大，冻结壁的设计应该按卸载的情况下进行[4-5]。理论分析方面，在平面轴对称的弹塑性分析中，圆筒状冻结壁的计算模型可以分为2类：一类是基于载荷结构法的弹塑性分析；另一类是基于围岩与冻结壁相互作用的弹塑性分析[6]，对于第一类，汪仁和、张常光等分别基于摩尔-库仑准则和统一强度理论探讨了冻结壁的应力场和位移场[7-8]；在第二类的研究中，胡向东 用等效应力荷载法代替岩土中原始应力构建冻结壁与围岩相互作用的分析模型，基于这一思想[9-10]，李栋伟、汪仁和等基于解除应力的概念建立在卸载状态下的冻结壁黏弹塑性计算模型，考虑冻结壁为非线性材料，从而获得冻结壁的应力场和位移场[11-14]。杨维好等基于围岩和冻结壁相互作用的计算模型，以弹塑性分析为基础探究了在不同屈服准则下冻结壁的设计问题[15-16]。

文献[11-16]对冻结壁和未冻结围岩进行了弹塑性分析，但都没有考虑由于地层冻结使岩土中的水结成冰而引起介质体积膨胀产生的冻胀力，其应力场将发生改变。在城市基础工程建设当中，岩土体的冻胀特性直接影响着人工冻结法施工技术的应用与发展[17-20]，针对冻结法凿井的施工特点，为了确定井筒开挖后围岩的应力和位移分布情况，需知道地层冻结后的应力场，考虑冻胀的影响，建立了井筒未开挖和开挖后的关于冻结壁及其周围土体的2个地应力场分布的计算模型，基于Drucker-Prager屈服准则，推导出冻结壁的弹塑性解析解。该计算模型可以更准确的反映实际工程情况，可以为冻结壁设计提供一定的理论依据，此外对数值模拟也具有一定的借鉴意义。

1　基本假设

基于冻结法施工特点，为了便于问题的分析，现做出以下假设

1)井筒未开挖时冻结壁及其周围土体是处于静水应力场中，并且断面为圆形；

2)按平面应变问题进行分析；

3)冻结壁及其周围土体都被视为各向同性的理想弹塑性材料；

4)井筒未开挖时冻结管的位置不发生变化，即冻结管处位移为零；

5)冻结完成时，冻结管内层土体呈完全冻结状态。

2　井筒未开挖时冻结壁与围岩的弹性解答

待冻结壁达到指定厚度后进行井筒开挖，但在冻结过程中土体发生冻胀并产生冻胀力，其地层应力也相应发生变化，所以在分析开挖之后冻结壁的弹塑性状态时，应是以冻结完成时的状态为起始状态。以冻结管的位置为边界把冻结壁分为外层冻结壁1，内层冻结壁2和开挖土体3，建立未开挖冻结壁的计算模型，如图1所示，其中r0为开挖半径；rf为冻结壁半径；rt为冻结管的位置；Pt为冻结管处的径向应力；Ph为冻结壁外的径向应力；P0为初始地应力。

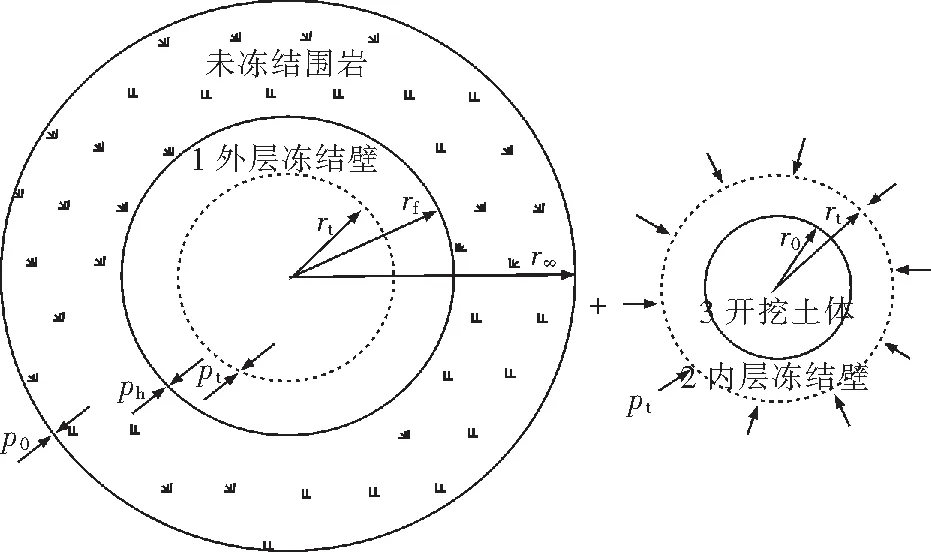
图1　未开挖时冻结壁计算模型Fig.1　Calculation model of frozen wall before the excavation

冻结壁的本构方程可以表示为[21]

(1)

式中Ef和μf分别为冻结壁的弹性模量和泊松比；Vσr和Vσθ分别为冻结壁和未冻结围岩中径向和环向的应力改变量；ε0为冻胀线应变，根据假设(3)，在每个方向的冻胀线应变都是一样的，因此冻胀线应变ε0=1/3εv，εv为体积冻胀率，可通过冻胀实验获得[22]。

未冻结围岩的本构方程可以表示为

(2)

式中E0和μ0分别为未冻结围岩的弹性模量和泊松比。

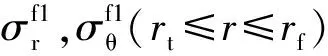
(3)

(4)

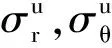
(5)

(6)

(7)

3　井筒开挖后各区域弹塑性解答

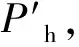
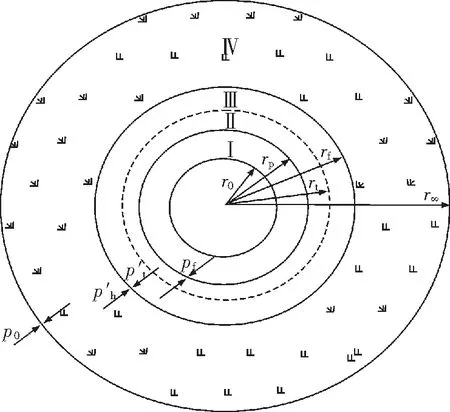
图2　开挖后冻结壁计算模型Fig.2　Calculation model of frozen wall after the excavation

3.1　内层冻结壁塑性区求解(Ⅰ，r0≤r≤rp)

平衡微分方程可以表示为

(8)

可用Drucker-Prager屈服准则来分析内层冻结壁塑性状态，其表达式为

(9)

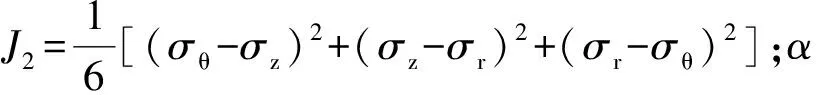
在工程中，经常用中间主应力系数b来反映中间主应力σz与最大主应力σθ和最小主应力σr的关系，它们之间的关系可表示为

(10)

根据式(9)和(10)，通过化简得到以下表达式

σθ=Mσr+N

(11)

把式(11)代入平衡方程(8)中，可得

(12)

式中，C1为积分常数

基于边界条件σr|r=r0=0，可得

(13)

把式(13)代入式(12)，结合式(10)和(11)，可获得区域Ⅰ的应力表达式

(14)

冻结壁的本构方程可以给出

(15)

塑性区的变形协调方程可以表示为

(16)

此外，在开挖后冻结壁计算模型中，冻结壁进入塑性状态时，应变可以表示为

(17)

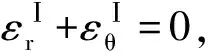
(18)

结合式(14)、(15)和(18)，根据边界条件εp|r=rp=0和几何方程，可以获得区域Ⅰ的径向位移

(19)

3.2　内层冻结壁弹性区求解(Ⅱ，rp≤r≤rt)

根据厚壁圆筒理论，可求得区Ⅱ的应力为

(20)

+(2uf-1)Pt}

(21)

3.3　外层冻结壁弹性区求解(Ⅲ，rt≤r≤rf)

同样可得区域Ⅲ的应力场

(22)

区域Ⅲ的前后应力差可以求出

(23)

根据式(15)、(22)和(23)，结合几何方程，可求解区域Ⅲ的径向位移[23]

(24)

其中，Gf为冻结壁的剪切模量，Gf=Ef/2(1+μf).

3.4　未冻区围岩弹性区求解(Ⅳ，rf≤r)

未冻结围岩弹性区的应力场可以给出

(25)

此区域的前后应力差为

(26)

根据式(2)、(25)和(26)，结合几何方程，可求得区域Ⅳ的径向位移

(27)

其中G0为未冻结围岩的剪切模量，G0=E0/2(1+u0).

4　算例与分析

参考文献[24]中的工程实例，位于甘肃的新庄煤矿风立井冻结法施工凿井中，冻结壁维护冻结期的平均温度为-10 ℃，冻结盐水温度为-30～-32 ℃.取第一水平冻结壁(深度为632 m)，冻结壁设计厚度4.5 m，冻结壁内径5.65 m，外径10.15 m，其他具体参数见表1.

表1　物理计算参数

4.1　计算结果

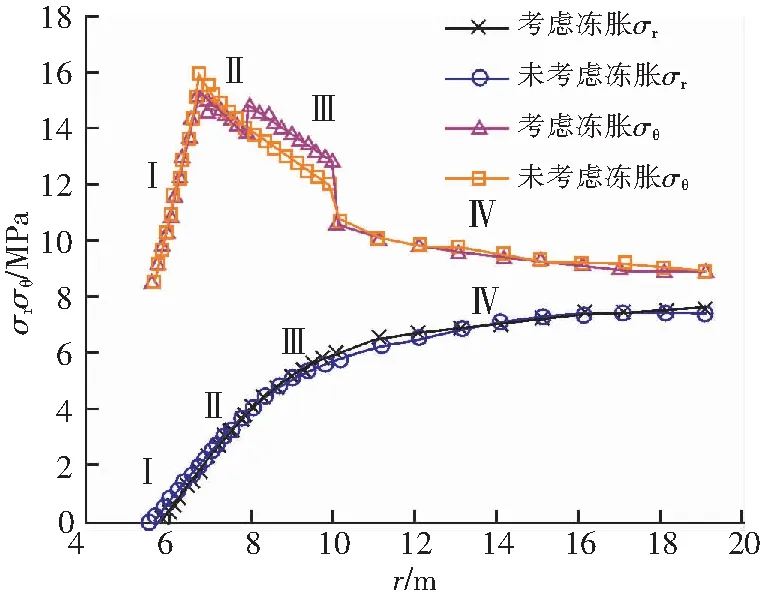
图3　开挖后应力场Fig.3　Stress field after the excavation

如图3所示，计算得到考虑冻胀和未冻胀情况下开挖后冻结壁和未冻结围岩的应力场。从结果可以看出，考虑冻胀影响后，导致初始地应力发生变化，由于Ⅲ区的初始应力是随半径变化的不定值，导致Ⅱ区和Ⅲ区环向应力不连续。而且环向应力曲线有明显的分区：内层冻结壁塑性区，内层冻结壁弹性区，外层冻结区，未冻结围岩。在冻结塑性区和内层冻结弹性区交界面处有最大环向应力15.587 MPa，径向应力随着半径的增大逐渐增大，最后趋向等于初始地应力。

图4表示考虑冻胀和未考虑冻胀情况下土体开挖之后的冻结壁和未冻结围岩的径向位移场。冻结壁内外边界处的位移，即在r=r0和r=rf处的位移分别为是66.59和54.31 mm.此外由图中对比分析可知，由于考虑冻胀的影响，初始地应力变化后导致Ⅲ区和Ⅳ位移相对增大。

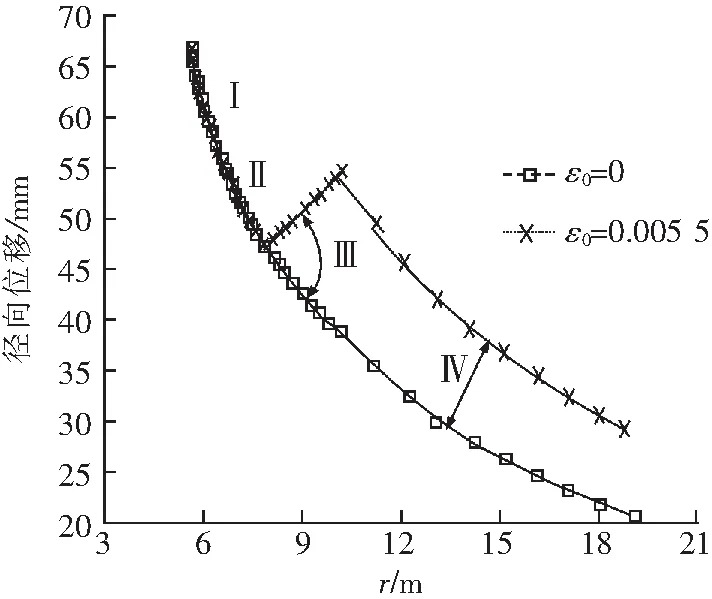
图4　开挖后位移场Fig.4　Displacement field after the excavation

通过计算，做出考虑冻胀和未考虑冻胀情况下界面处应力和塑形半径的对比分析表格，见表2，分析可知在考虑冻胀的影响之后塑性半径变小，冻结管处所受的应力相对减小，冻结壁内外边界处的应力增大。

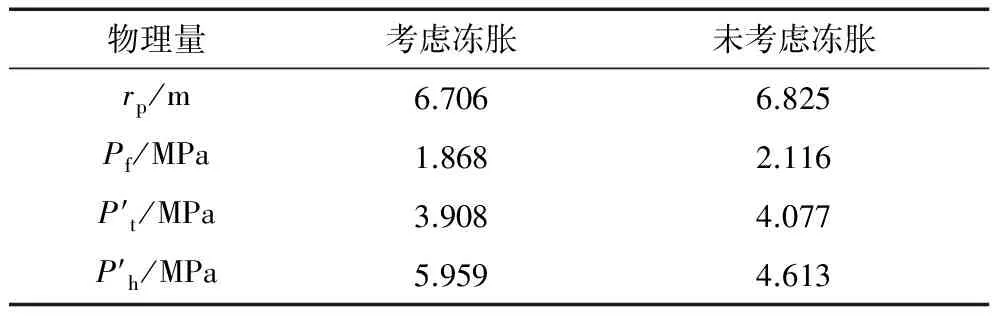
表2　在不同条件下塑形半径和各界面处应力大小比较

4.2　参数分析

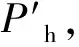
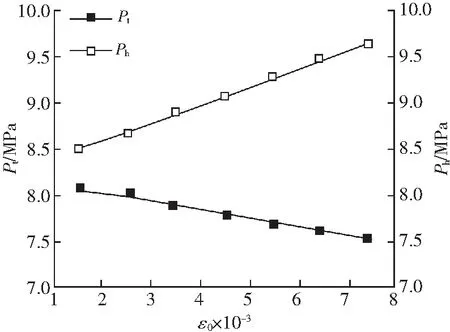
图5　ε0与Pt和Ph的关系Fig.5　Relationship between ε0 and Pt，Ph

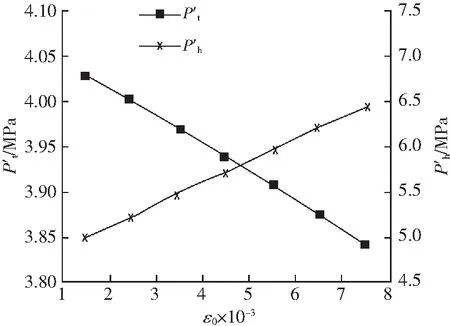
图6　ε0与和的关系Fig.6　Relationship between ε0 and

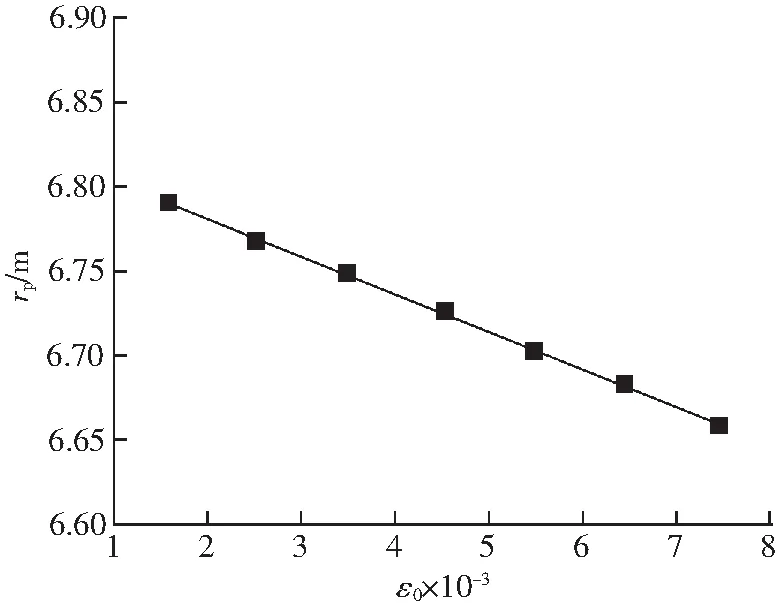
图7　ε0与rp的关系Fig.7　Relationship between ε0 and rp

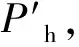
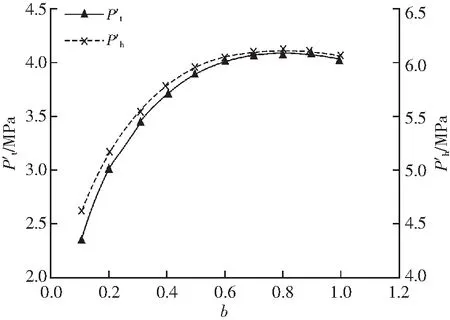
图8　b与和的关系Fig.8　Relationship between b and

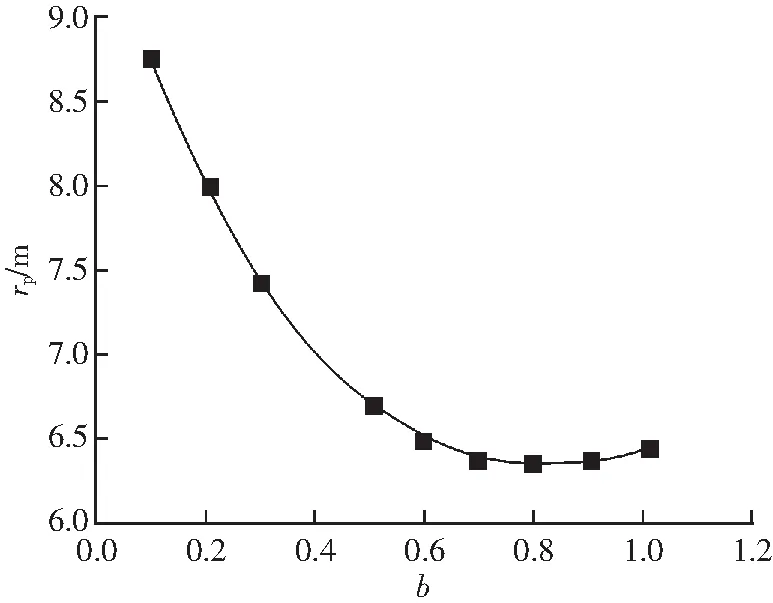
图9　b与rp的关系Fig.9　Relationship between ε0 and rp

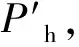
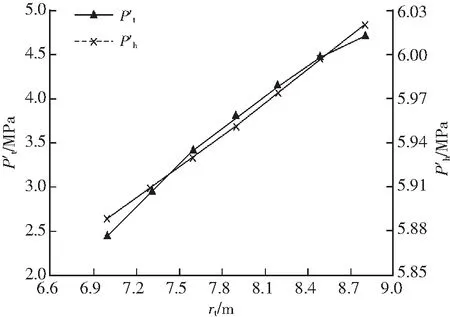
图10　rt与和的关系Fig.10　Relationship between rt and

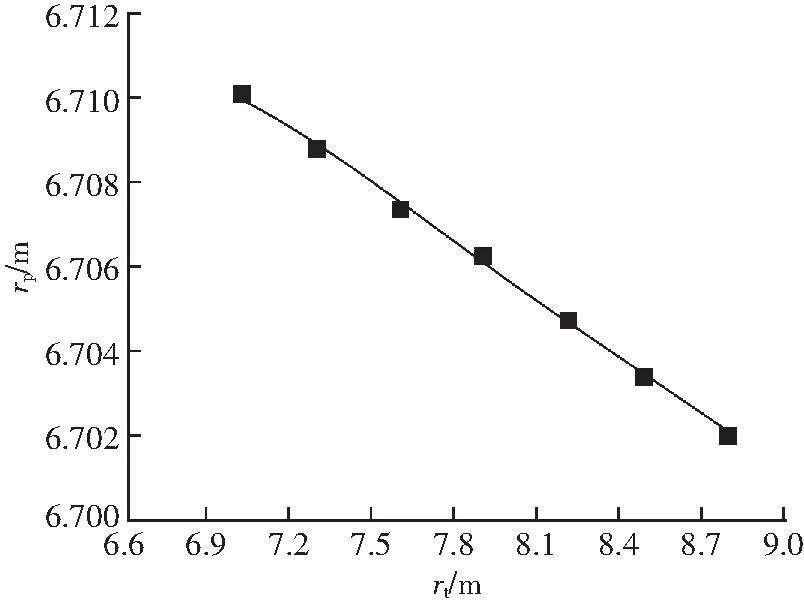
图11　rt与rp的关系Fig.11　Relationship between rt and rp

5　结　论

1)考虑在开挖之前冻胀对地层应力的影响，推导出应力场重分布之后冻结壁及其周围土体的应力表达式，从而推导出了井筒开挖后围岩和冻结壁的弹塑性解，可为数值模拟提供一定理论依据；

2)通过算例分析，可得冻结壁及其周围土体的应力场和位移场分布；考虑冻胀作用，导致环向应力场明显分区，如图3所示；

3)在考虑冻胀的影响之后，导致Ⅱ区和Ⅲ区的环向应力不连续，井筒开挖后的塑性半径、冻结管处所受的应力减小，而冻结壁外边界处的应力相对增大；

4)通过参数分析可得在不同的冻胀线应变、中间主应力系数和冻结管的位置条件下，对开挖前后冻结壁外应力，开挖前后冻结管处应力以及塑性半径5个量的影响规律；

5)该计算模型的建立是在开挖土体呈完全冻结状态的基础上进行的，开挖土体为未冻结状态的问题有待进一步研究。

参考文献(References)：

[1]曹雪叶，赵均海，张常光.基于统一强度理论的冻结壁弹塑性应力分析[J].岩土力学，2017，38(3)：769-774，809.

CAO Xue-ye，ZHAO Jun-hai，ZHANG Chang-guang.Elastoplastic stress analysis of frozen soil wall based on unified strength theory[J].Rock and Soil Mechanics，2017，38(3)：769-774，809.

[2]蔡海兵，彭立敏，郑腾龙.隧道水平冻结壁强制解冻期地表沉降的预测方法[J].岩土力学，2015，36(12)：3516-3521，3530.

CAI Hai-bing，PENG Li-min，ZHENG Teng-long.A method for predicting ground surface settlement in the artificial thawing period of tunnel horizontally frozen wall[J].Rock and Soil Mechanics，2015，36(12)：3516-3521，3530.

[3]石荣剑，岳丰田，张勇，等.盾构地中对接冻结加固模型试验(Ⅰ)——冻结过程中地层冻结温度场的分布特征[J].岩土力学，2017，38(2)：368-376.

SHI Rong-jian，YUE Feng-tian，ZHANG Yong，et al.Model test on freezing reinforcement for shield junction Part 1：Distribution characteristics of temperature field in soil stratum during freezing process[J].Rock and Soil Mechanics，2017，38(2)：368-376.

[4]Ma W，Chang X X.Analyses of strength and deformation of an artificially frozen soil wall in underground engineering[J].Cold Regions Science and Technology，2002，34(1)：11-17.

[5]Ma W，Chang X X.Effect of consolidating process on stress-strain behaviour of artificially frozen soil[C]//Proceedings of the International Symposium on Ground Freezing and Frost Action in Soils，Louvan-la-Neuve，Belgium.A.A.Balkema，Rotterdam，2000：151-154.

[6]管华栋，周晓敏.基于围岩相互作用的冻结壁塑性分析对比研究[J].岩土力学，2017，38(3)：1-7.

GUAN Hua-dong，ZHOU Xiao-min.Comparative study of elastoplastic of frozen wall based on interaction of surrounding rock[J].Rock and Soil Mechanics，2017，38(3)：1-7.

[7]汪仁和，李栋伟，王秀喜.摩尔-库仑强度准则计算冻结壁应力场和位移场[J].工业建筑，2005，35(10)：40-42.

WANG Ren-he，LI Dong-wei，WANG Xiu-xi.Calculating frozen wall stress and displacement fields by Mohr-Coulomb strength criterion[J].Industrial Construction，2005，35(10)：40-42.

[8]张常光，赵均海，魏雪英.基于统一强度理论冻结壁应力场和位移场研究[J].地下空间与工程学报，2008，4(3)：465-469.

ZHANG Chang-guang，ZHAO Jun-hai，WEI Xue-ying.Investigation the stress field and displacement field on the frozen wall based on the unified strength theory[J].Chinese Journal of Underground Space and Engineering，2008，4(3)：465-469.

[9]胡向东.卸载状态下与周围土体共同作用的冻结壁力学模型[J].煤炭学报，2001，26(5)：507-511.

HU Xiang-dong.A mechanical model of interaction of frozen soil wall and surrounding earth mass in unload state[J].Journal of China Coal Society，2001，26(5)：507-511.

[10]胡向东.卸载状态下冻结壁外载的确定[J].同济大学学报：自然科学版，2002，30(1)：6-10.

HU Xiang-dong.Determination of load on frozen soil wall in unloaded state[J].Journal of TongJi University：Natural Science Edition，2002，30(1)：6-10.

[11]李栋伟，汪仁和.弹塑性本构模型计算冻结壁应力场和位移场[J].低温工程，2005(5)：53-55，58.

LI Dong-wei，WANG Ren-he.Elastic and plastic model for calculation of frozen wall stress and displacement field[J].Cryogen Ics，2005(5)：53-55，58.

[12]李栋伟，张世银，汪仁和，等.粘弹塑性冻结壁计算理论研究[J].煤炭工程，2006(1)：60-62.

LI Dong-wei，ZHNAG Shi-yin，WANG Ren-he.Study on calculation theory for mine shaft viscous-elastic-plastic freezing wall[J].Coal Engineering，2006(1)：60-62.

[13]汪仁和，李栋伟.深井冻结壁粘弹塑性力学分析[J].安徽理工大学学报：自然科学版，2006，26(2)：17-19.

WANG Ren-he,LI Dong-wei.Analysis of visco-elasto-plastic mechanics for frozen wall in deep-shaft[J].Journal of Anhui University of Science and Technology：Natural Science Edition，2006，26(2)：17-19.

[14]汪仁和，李栋伟，王秀喜.井筒开挖下非线性冻结壁的应力场和位移场计算[J].上海交通大学学报，2005，39(11)：1862-1865.

WANG Ren-he，LI Dong-wei，WANG Xiu-xi.Nonlinear model calculating frozen wall stress and displacement fields in shaft excavation[J].Journal of ShangHai Jiaotong University，2005，39(11)：1862-1865.

[15]杨维好，杨志江，韩涛，等.基于与围岩相互作用的冻结壁弹性设计理论[J].岩土工程学报，2012，34(3)：516-519.

YANG Wei-hao，YANG Zhi-jiang，HAN Tao，et al.Elastic design theory of frozen soil wall based on interaction between frozen soil wall and surrounding rock[J].Chinese Journal of Geotechnical Engineering，2012，34(3)：516-519.

[16]杨维好，杨志江，柏东良.基于与围岩相互作用的冻结壁弹塑性设计理论[J].岩土工程学报，2013，35(1)：175-180.

YANG Wei-hao，YANG Zhi-jiang，BO Dong-liang.Elastic-plastic design theory of frozen soil wall based on interaction between frozen wall and surrounding rock[J].Chinese Journal of Geotechnical Engineering，2013，35(1)：175-180.

[17]胡坤，周国庆，李晓俊，等.不同约束条件下土体冻胀规律[J].煤炭学报，2011，36(10)：1653-1658.

HU Kun，ZHOU Guo-qing，LI Xiao-jun，et al.Experiments on frost heave of artificial frozen soils with different constraints[J].Journal of China Coal Society，2011，36(10)：1653-1658.

[18]Selvadurai A P S，Hu J，Konuk I．Computational modeling of frost heave induced soil-pipeline interaction I modeling of frost heave[J].Cold Regions Science and Technology，1999，29(3)：215-228．

[19]Viklander P.Permeability and volume changes in till due to cyclic freeze/thaw[J].Canadian Geotechnical Journal，1998，35(3)：471-477.

[20]Qi J L，Ma W，Sun C S，et al.Seismic response of seasonally frozen ground[J].Cold Regions Sciences and Technology，2006，44(2)：111-120.

[21]Feng Q，Jiang B S，Zhang Q，et al.Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels[J].Cold Regions Science and Technology，2014，108：59-68.

[22]Lai Y M，Wu H，Wu Z W.Analytical viscoelastic solution for frost force in cold-region tunnels[J].Cold Regions Science and Technology，2000，31(3)：227-234.

[23]冯强，王刚，蒋斌松.季节性寒区隧道围岩融化分析的一种解析计算方法[J].岩土工程学报，2015，37(10)：1835-1843.

FENG Qiang，WANG Gang，JIANG Bin-song.Analytical method for thawing analysis of surrounding rock in seasonal cold region tunnels[J].Chinese Journal of Geotechnical Engineering，2015，37(10)：1835-1843.

[24]李庆平.新庄煤矿风立井冻结壁与井壁相互作用研究[D].西安：西安科技大学，2014.

LI Qing-ping.Research on the interaction between frozen wall and shaft lining of Xinzhuang coal mine air shaft[D].Xi’an：Xi’an University of Science and Technology，2014.

[25]张小波，赵光明，孟祥瑞.基于Drucker-Prager屈服准则的圆形巷道围岩弹塑性分析[J].煤炭学报，2013，38(S1)：30-37.

ZHANG Xiao-bo，ZHAO Guang-ming，MENG Xiang-rui.Elastoplastic analysis of surrounding rock on circular roadway based on Drucker-Prager yield criterion[J].Journal of China Coal Society，2013，38(S1)：30-37.