弹体低速正穿甲砂卵石靶的数值模拟
2018-04-11邓勇军孙加超吴东旭
邓勇军 姚 勇 孙加超 吴东旭
(1. 西南科技大学土木工程与建筑学院 四川绵阳 621010;2. 工程材料与结构冲击振动四川省重点实验室 四川绵阳 621000)
砂卵石在工程中多用于机场跑道、公路等的基层中,并以填料的形式存在,其在服役期间会受到爆炸或穿甲等强冲击荷载的作用。国内外学者在土体受冲击载荷作用方面做了大量的试验和数值模拟研究,也取得了相应的研究成果[1-5]。砂卵石属于粒径较大的粗粒土,其内部颗粒尺寸分布和空间分布的不均匀性对弹体穿甲砂卵石时的弹道偏转、穿甲深度和毁伤效果都是不可忽略的,且室内外试验的试验成本较高、可重复性差、试验数据离散,故对于该问题的研究,数值模拟具有较强的优势。随着细观力学理论的发展和高速度大容量电子计算机的出现,研究人员开始利用基于细观力学层次的数值模型来研究非均质多相脆性材料的宏观力学性能[6-8]。对粗粒土的数值模拟研究大致分为以下两种不同的途径:一种是基于有限元法的数值模拟,该方法仍然将材料视为连续的介质;另一种则是基于离散元法的数值模拟,其主要思想是将材料离散成有限数量的颗粒单元,通过模拟颗粒单元之间的相互作用与相对运动,从而反映材料的宏观特性。砂卵石正是由有限数量的土石颗粒组成,完全符合离散元法的思想,并且离散元法是以C语言为程序代码,通过语言的控制实现模型的建立,可以将砂卵石中土/石颗粒的粒径大小、位置分布等都能够较为精准地设定,从而符合实际模型的需要[9-11]。本文以离散元模型为基础建立了砂卵石靶的正穿甲数值模型,分析了穿甲过程中弹体、卵石的受力情况,并讨论了卵石级配、围压等参数对穿甲性能的影响。
1 砂卵石靶穿甲数值模型的建立
颗粒离散元法是以C语言为基本程序代码,能够将真实砂卵石的级配需要(土石颗粒的粒径分布情况、土石颗粒的含量百分比分布情况)通过语言的形式输入,并以图像的方式输出。离散元法中的两个基本对象——墙体和颗粒,墙体用于模拟模型中的铝板,颗粒用于模拟砂卵石土中的土石颗粒。
土石颗粒建模的命令格式如下:
GENERATE x xl xu y yl yu z zl zu radius rl ru id il iu
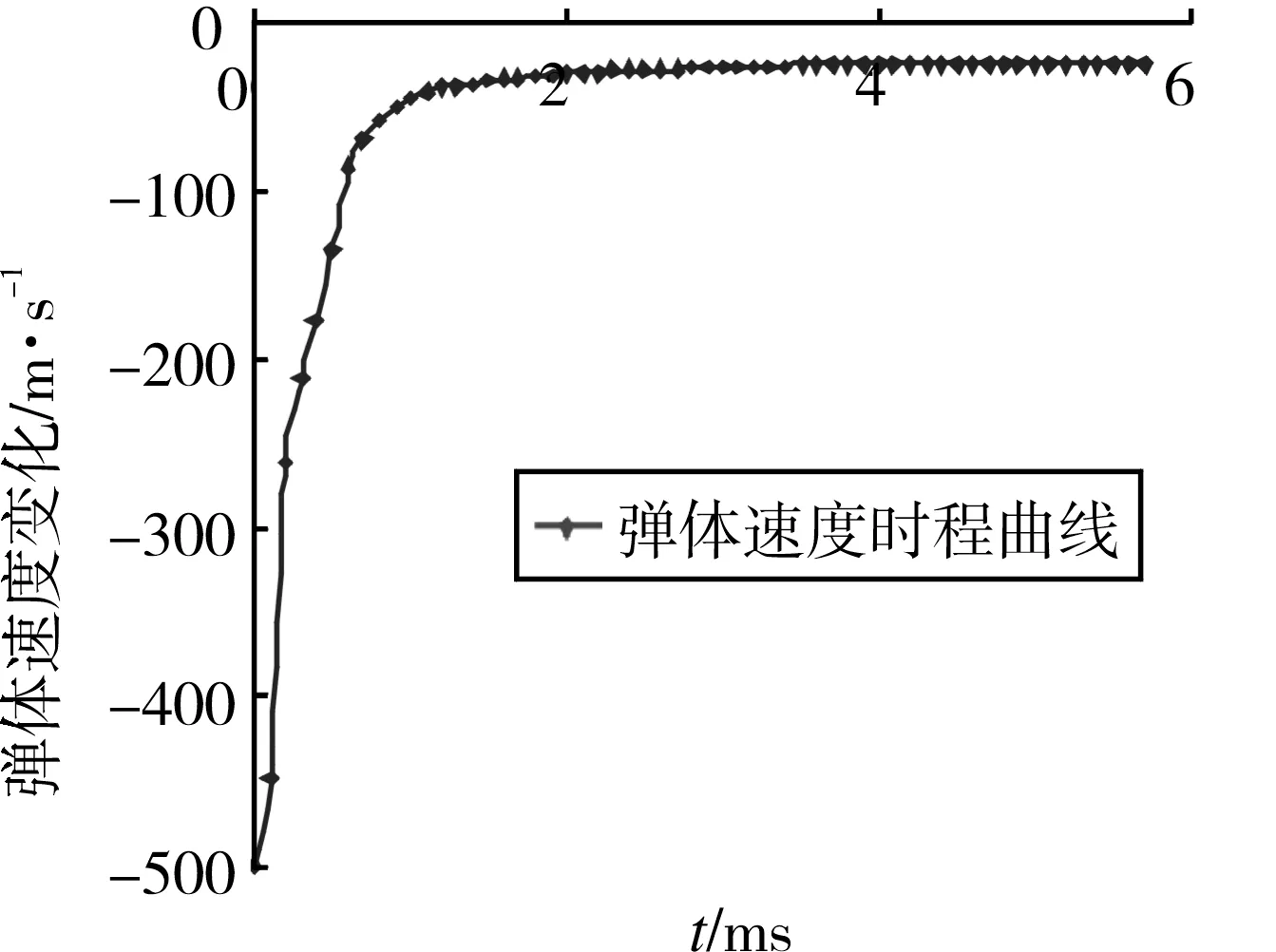
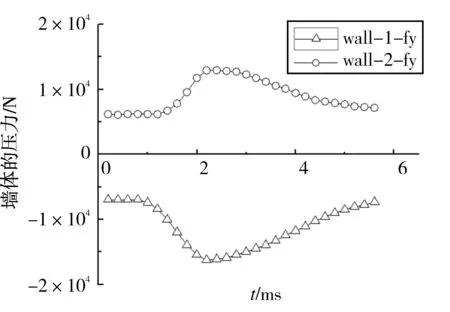
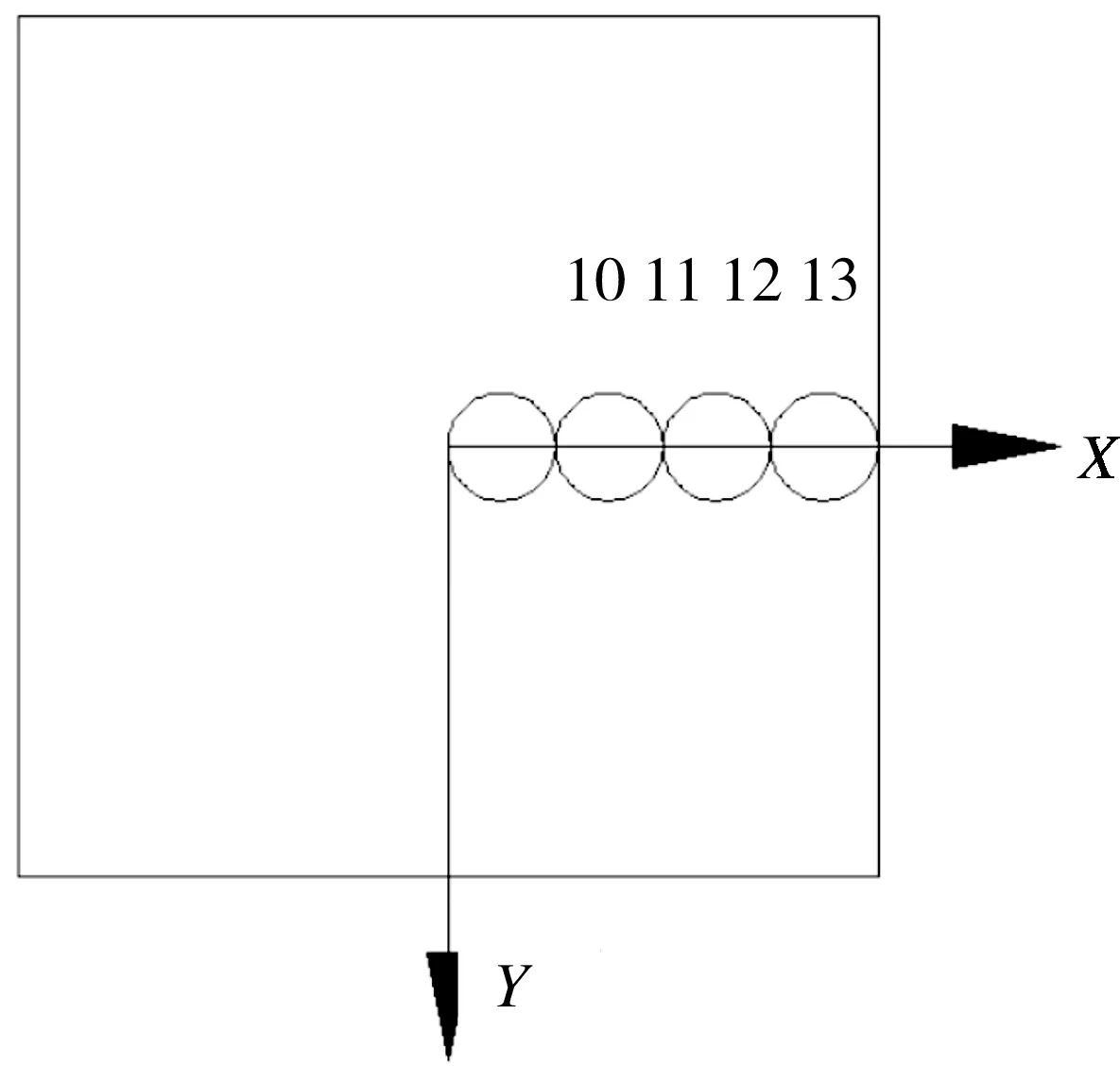
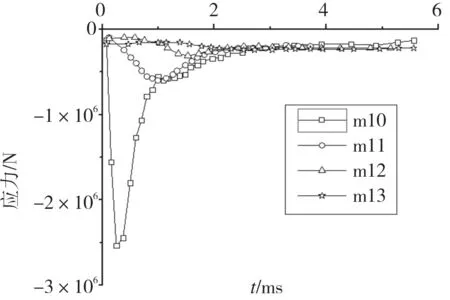
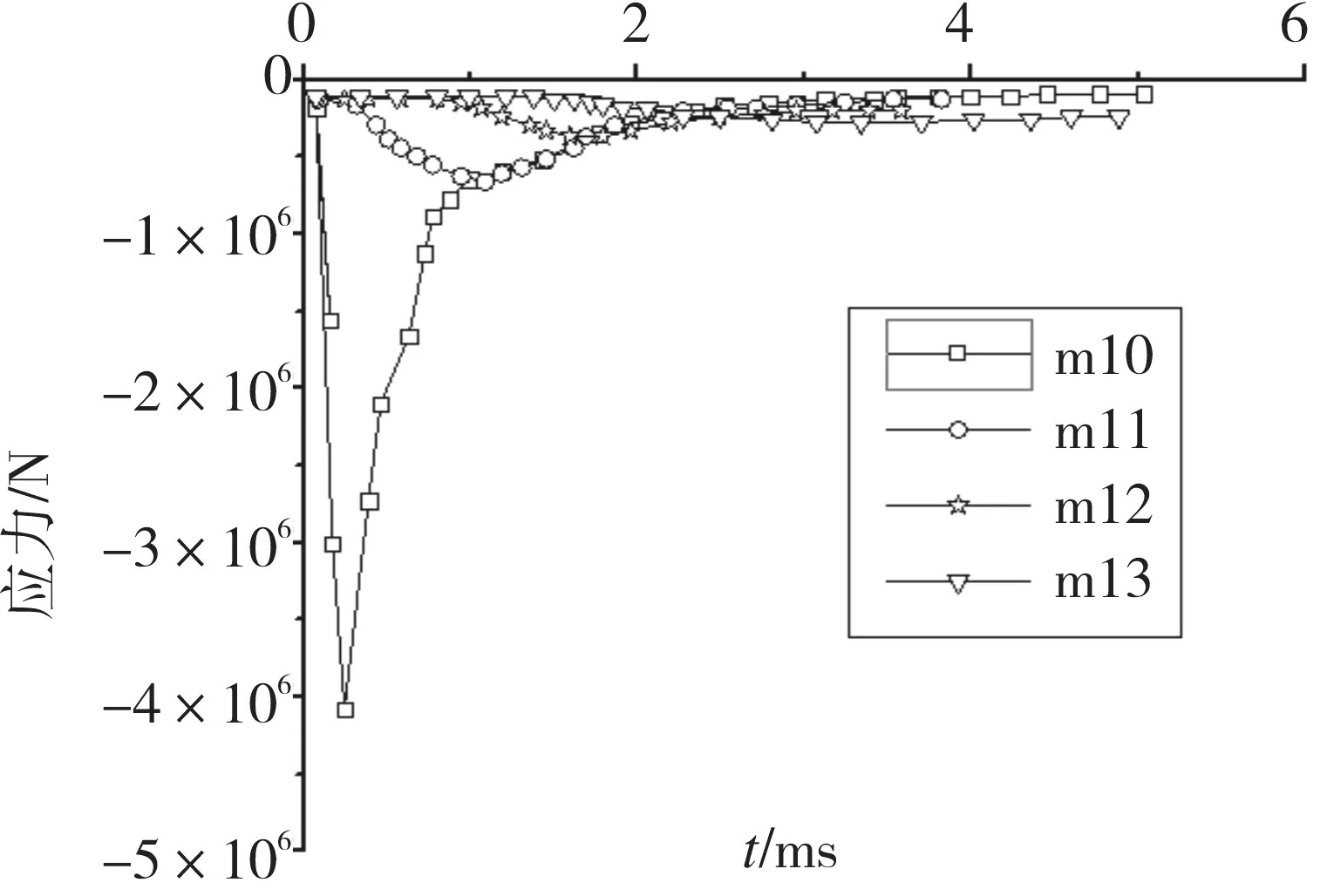
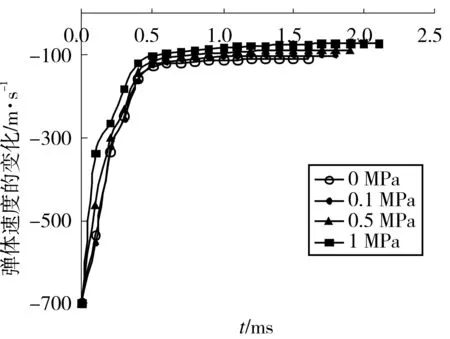
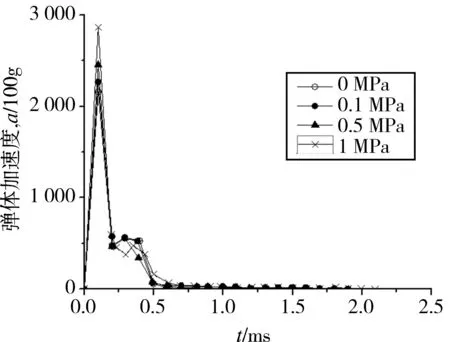
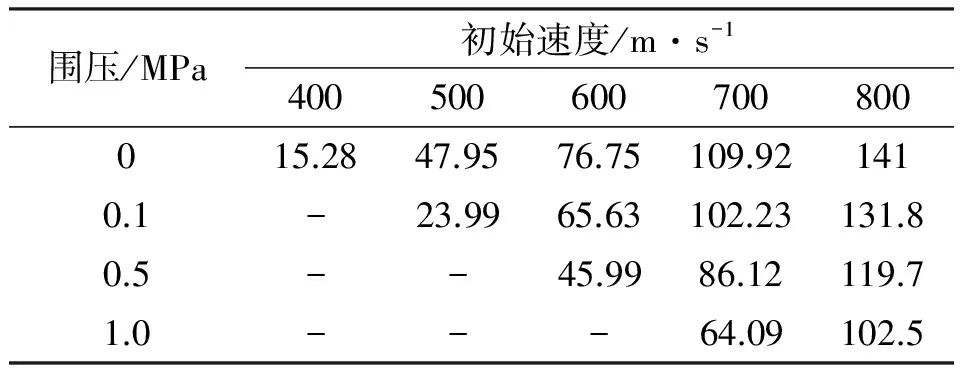
即在xl 由于砂卵石土属于散体材料,不像混凝土那样容易成形,所以必须将松散的砂卵石土固定起来,以便弹体的穿甲。通过在模型中建立6面墙体形成一个立方体的盒子来实现,将砂卵石放置于该立方体盒子中。砂卵石在工程中并非自然堆积,而通常是处于一定围压下的,故在建立砂卵石穿甲模型的时候,通过控制墙体的相对运动,使得模型达到设定的围压。由于离散元模型中建立的墙体是完全刚性的,墙体的运动需要用户自己定义。为保证穿甲计算的进行,此处采用等效代换的思想,将迎弹面的墙体用4面墙体来代替,并在4面墙体中留出大于弹径的方形孔,此方法解决了弹体不能打入砂卵石土的问题。出靶面墙体也做同样处理,不过考虑到弹体可能的偏转,出靶面预留方孔的边长应比入射面稍大。图1是铝板的墙体模型以及等效代换的开孔墙体模型。 数值模拟中砂卵石土模型的尺寸为400 mm×400 mm×150 mm,弹体直径为25 mm,所以将入射面的方孔边长设定为30 mm,背面方孔的边长设定为50 mm,如图1(c)所示,其中砂卵石细观力学参数通过直剪试验获得,如表1所示。弹丸弹径为25 mm,长度为143.7 mm,尖卵形弹头满足CRH=3.0,穿甲数值模型如图2所示。 图1 铝板墙体模型及等效代换Fig.1 Aluminum plate model and the equivalent substitution 参数ρ/kg·m-3Ec/MPakn/ksμn取值265062.52.50.400.35 图2 弹体及离散元模型Fig.2 The discrete element model of the projectile and target 砂卵石土靶板的长宽均为400 mm,厚度为150 mm,为了模拟弹体横向穿靶的过程,即弹体沿着靶板的厚度方向穿靶,故重力加速度的方向设置在x轴的正方向,考虑一定级配的砂卵石土在围压为0.1 MPa的情况下,弹体以500 m/s的初始速度穿甲砂卵石土靶板的初始位置,图3是弹体穿透砂卵石靶板时的情形。 图3 弹体出靶时的位置(侧视/正视)Fig.3 The location of the projectile perforated 弹体以500 m/s的初始速度穿甲砂卵石模型,不同时刻弹体的位置及砂卵石土的响应见图4。在弹体冲击作用下,弹体周围的卵石在穿甲过程中获得了部分动能,且由于卵石极易流动,靶体背面破孔处形成射流,由于背面预留方孔大小的限制,粒径较小的砂卵石土颗粒随弹体运动喷出,而粒径较大的颗粒则不容易被弹体从背面带出来,而是被弹体挤压到另一侧。 图4 弹体穿甲砂卵石靶的过程Fig.4 The process of the projectile perforating the sandy pebble with different grading 弹体在穿甲砂卵石靶板的过程中速度的衰减情况和运动方向受力的情况见图5和图6。从图中可以看出,弹体在穿甲砂卵石靶板的过程中,受到砂卵石的反作用力主要集中在第一个毫秒以内,在这段时间内弹体的速度瞬间从500 m/s衰减到50 m/s左右,且此时弹体的头部已经穿出了靶板,此后弹体受到的阻力主要来源于弹体与砂卵石土之间的摩擦。 图5 弹体的速度时程曲线Fig.5 The acceleration curve of the projectile 图6 弹体运动方向受力的变化Fig.6 The stress changes of the projectile in motion direction 弹体完全出靶时的速度约为24 m/s,然而从Hanchak[12]穿甲混凝土靶板的试验研究中可以看出,弹体以434 m/s的初始速度穿甲强度为48 MPa的混凝土,弹体出靶的速度为200 m/s左右。由此可以看出,弹体在穿甲砂卵石的过程中,很可能是由于弹径比的原因(模型中最大颗粒粒径为50 mm,弹径为25 mm),弹体打到粒径较大的颗粒,才可能出现这样的情况。 由于穿甲方向上的两面墙体被分别用四面墙体等效代换了,在穿甲过程中将不考虑其受力,仅考虑4面侧墙的响应,其编号与图2(a)一致。通过监测4面墙体在弹体穿甲砂卵石过程中的受力情况,得到了4面墙体受力随时间的变化关系如图7和图8所示。 由于重力加速度的方向设置在x的正方向,如果在模型中颗粒完全对称的情况下,墙体1和2在y方向的受力应该是完全相等的,然而从图7可以看出,墙体2的受力要比墙体1的受力稍大一些,因为级配的关系使得模型中的粗细颗粒的分布非常不均;由于颗粒的重力作用在墙体3的x方向,故墙体3在x方向上的受力要比墙体4的受力大得多。由于整个模型中存在0.1 MPa的初始应力,故四面墙体的受力变化的起始点都不是从0开始的。从图中还可以看出,墙体在弹体穿甲过程中受力的最大值几乎比初始受力大2倍。 图7 墙体1和2在y方向的受力变化Fig.7 The stress changes of plate 1 and 2 in y direction 图8 墙体3和4在x方向受力变化Fig.8 The stress changes of plate 3 and 4 in x direction 颗粒离散元法允许用户在模型的任意位置设置一个measure sphere,即测量圆,测量圆可以监测一个球形区域内的颗粒在任意时刻的孔隙比、应变率以及应力。为了研究弹体穿甲过程中砂卵石内部的一些应力变化以及传递的一些情况,在z为0的平面上,从坐标原点开始,沿着x轴正方向,等间距安装了4个半径为25 mm的测量圆,测量圆的球心均位于x轴上(x=25,75,125,175 mm),如图9所示,测量圆的编号从左到右依次为10,11,12和13。 图10-图12是弹体穿甲过程中4个测量圆内3个方向上应力随穿甲时间的变化情况,从图中颗粒看出,测量圆10距离弹体穿甲的位置最近,弹体穿甲时其内部应力的变化非常大,约为初始值的30~40倍;其后再通过颗粒与颗粒之间的相互作用,将力传递给周围的颗粒,测量圆11内的应力变化近似为初始值的6~7倍,测量圆12内的应力变化近似为初始值的4倍左右,测量圆13内的应力变化几乎为初始值的2倍左右。据此可以推测,砂卵石模型的宽度再增加1/2,穿甲过程中砂卵石对周边的影响可以忽略。 图9 4个测量圆的布置位置Fig.9 The location of the four measuring circles 图10 4个测量圆内x方向的应力变化Fig.10 The stress changes in x direction in the four measuring circles 通过不同级配砂卵石抗剪特性的研究分析发现,级配组成对砂卵石的抗剪特性有很大的影响[13]。为了研究颗粒的级配组成对砂卵石穿甲过程的影响,在数值模拟中考虑了以下3种颗粒级配组成(该部分简称JP1,JP2,JP3),见表2。 图11 4个测量圆内y方向的应力变化Fig.11 The stress changes in y direction in the four measuring circles 图12 4个测量圆内z方向的应力变化Fig.12 The stress changes in z direction in the four measuring circles 根据砂卵石的颗粒级配组成,运用前面所述的方法在边长为400 mm×400 mm×150 mm的立方体盒子内生成砂卵石穿甲模型(模型中颗粒的最小尺寸为10 mm)。模型中的围压都设定为0.1 MPa。3种级配砂卵石的数值模型如图13所示。 表3给出了在相同的围压状态下(0.1 MPa),不同初始速度穿甲3种级配砂卵石靶的剩余速度。从表中数据可以看出,颗粒的级配组成对弹体穿甲砂卵石土的剩余速度的影响非常大。如弹体以500 m/s的初始速度穿甲3种级配砂卵石土模型,级配1组和级配2组分别考虑了砂卵石土颗粒级配的组成,穿出砂卵石土的剩余速度分别为23.99 m/s和84.59 m/s,级配3组则没有考虑颗粒级配的组成,将砂卵石考虑成粒径均匀的颗粒,弹体穿出级配3组砂卵石土的剩余速度为207.57 m/s。 表2 砂卵石土级配组成Table 2 The gradation composition of sandy pebble soil 图13 3种级配砂卵石的离散元模型Fig.13 The discrete element model of sandy plbbles with three kinds of gradation 级 配初始速度/m·s-1300400500600700800JP1--23.9965.63102.2131.83JP2-40.1884.59126.97175.2222.92JP368.3137.1207.57278.3344407.93 为了分析弹体穿甲3种级配砂卵石剩余速度的差异来源,取出了3种级配砂卵石在弹体经过的圆柱形区域内的砂卵石颗粒,如图14所示。弹体在穿甲级配1组砂卵石的过程中可能会撞击到的砂卵石颗粒,其中有4个粒径较大的颗粒,该4个颗粒的粒径在20~40 mm之间,由于弹体的弹径为25 mm,则弹径与砂卵石颗粒粒径的比值最大为1∶1.6。弹体穿甲级配2组砂卵石的过程中可能会撞击到的砂卵石颗粒,其中有一个粒径较大的颗粒可能会在穿甲过程中与弹体产生直接接触,该颗粒的粒径在20~40 mm之间,则弹径与砂卵石颗粒粒径的比值最大为1∶1.6。弹体穿甲级配3组的过程中可能会撞击到的砂卵石土颗粒,均匀颗粒的粒径为10 mm,则弹径与砂卵石土颗粒粒径的比值为2.5∶1。 图14 穿甲过程中弹体直接作用的砂卵石颗粒Fig.14 The sand gravel particles of the projectile impacted directly during perforation 在不考虑砂卵石颗粒被弹体打碎的情况下,弹体接触到砂卵石的瞬间,将对砂卵石颗粒施加一定的作用力,将砂卵石土颗粒挤开,继续沿着运动方向运动;同时砂卵石给予弹体一定的反作用力,使得弹体的速度降低(弹体加速度时程曲线见图15)。如果弹体与粒径较大的颗粒接触时,粒径较大的颗粒所占的空间体积越大,由于初始围压的存在,大粒径颗粒被挤开时所需要的能量也就越大,即弹体能量的衰减越多,同时弹体受到砂卵石的反作用力也越大,此反作用力就是导致弹体速度衰减和弹体偏转的主要原因。 结合图14和图15可以看出,弹体在穿甲级配1组砂卵石土的过程中,弹体可能与4个粒径较大的颗粒相互作用,弹体的加速度时程曲线可以看出,弹体在级配1组中运动的加速度时程曲线存在明显的二次波峰,即弹体在挤开粒径较大的颗粒之后再次撞击到了其他的大粒径的颗粒;在级配2组中可能与一个粒径较大的颗粒直接接触,在级配3组中没有和粒径较大的颗粒直接接触。所以在相同的围压下,弹体穿出第一种级配砂卵石土时的剩余速度最小,而穿出第三种级配砂卵石土时的剩余速度最大。因此,导致剩余速度差异的主要因素是弹径比的差异以及与弹体产生直接作用的粗颗粒的数量。 图15 弹体穿甲过程中运动方向合力的时程曲线Fig.15 The time history curve of net force during perforation 砂卵石在实际工程应用中多数是被用作处理软弱地基的填料,故其通常处于带围压的工作状态。对于弹体穿甲砂卵石的分析来说,围压对穿甲结果的影响是不可忽略的,一般来说,砂卵石所处的围压越大,砂卵石的密实程度越大,弹体穿甲砂卵石所需要的能量也越大,即弹体越不容易打入砂卵石。 为了研究围压对弹体穿甲砂卵石的影响过程,以JP1为基础建立砂卵石穿甲模型,选择4种砂卵石的围压:0,0.1,0.5,1 MPa,初始速度700 m/s。图16、图17是弹体初始速度为700 m/s的情况下,穿甲4种不同围压的砂卵石的速度、加速度时程曲线。 由图16可以看出,模型中砂卵石所处的围压越大,弹体的速度衰减也越快,弹体穿出砂卵石靶所需要的时间也越长。当砂卵石土所处围压为0 MPa时,弹体穿出砂卵石靶板的速度约为110 m/s,当围压逐渐增大至0.1,0.5,1 MPa时,弹体的出靶速度依次为106,86,64 m/s,由此可以看出,围压在一定程度上增大了穿甲过程中弹体的阻力。分析可知:砂卵石土所处的围压越大,其密实度也越大,砂卵石土颗粒被弹体挤压开所需要做的功就越大,所以弹体穿出砂卵石土靶板所需要消耗的能量也越大。 图17为弹体以700 m/s的速度穿甲不同围压下的砂卵石土的加速度时程曲线。图17表明,弹体撞击靶体的瞬间,加速度出现第一个峰值,且围压越大峰值越大,意味着弹体受到来自周围砂卵石较大的作用力。而加速度时程中出现的二次波峰,可能是弹体在侵入靶体之后,遇到了内部的粒径较大的颗粒,此时弹体的速度小于初始速度,故加速度二次波峰的数值相对于第一个波峰来说小很多。 图16 不同围压下弹体的速度时程曲线Fig.16 The velocity time-history curve of the projectile under different confining pressures 图17 不同围压下弹体的加速度时程曲线Fig.17 The acceleration time-history curve of projectile under different confining pressures 为了进一步研究围压对弹体穿甲砂卵石土的影响,分别对不同初始速度穿甲砂卵石土靶板进行了数值模拟研究,数值模拟中考虑了5个弹体初始速度,400,500,600,700,800 m/s,砂卵石土处于4个不同的围压状态,即0,0.1,0.5,1 MPa,弹体穿甲砂卵石土靶板的出靶速度列于表4。从表4可以看出,在速度比较低的情况下,围压对弹体穿甲砂卵石土的速度衰减较为明显,但随着弹体速度的增大,围压对弹体穿出砂卵石土的剩余速度的影响出现衰减的趋势。 表4 不同工况下弹体的出靶速度(单位:m·s-1)Table 4 The residue velocity of the projectile in different cases(unit:m·s-1) 本文采用离散元数值方法对砂卵石靶的穿甲问题进行了数值模拟,得到以下结论:(1)采用离散元法可以较好模拟弹体穿甲砂卵石靶的过程,且可以得到卵石在穿甲过程中的挤压运动现象。(2)卵石级配对于弹体穿甲的剩余速度有较大影响,并与弹道周围的卵石粒径大小有关,其中单一级配下弹体剩余速度远大于连续级配。 (3)弹体在穿甲砂卵石靶的过程主要是以挤压的形式作用于周围砂卵石,故围压越高,卵石密实程度越高,弹体穿甲的能量衰减越多。 [1]FORRESTAL M J, LUK V K. Penetration into soil targets[J]. Int J Impact Eng 1992, 12:427-44. [2]FORRESTAL M J, GRADY D E. Penetration experimental for normal impact into geological targets[J]. Int J Solids Struct. 1982, 18:229-234. [3]BAKULIN V N, OVCHAROV P N, POTOPAKHIN V A. Experimental study of deformation of thin conical shells during penetration into soil[J]. Mechanics of solids, 1988, 23: 183-186. [4]MENARD L, BOROISE Y. Theoretical and practice aspects of dynamic consolidation[J]. Geotechnique,1975,25(1):3-18. [5]王汝恒,贾彬,邓安福,等.砂卵石土动力特性的动三轴试验研究[J].岩石力学与工程学报,2006,25(2):4059-4064. [6]邢纪波,俞良群,王泳嘉. 三维梁-颗粒模型与岩石材料细观力学行为模拟[J]. 岩石力学与工程学报, 1999, 16(6): 627-630. [7]王宗敏, 邱志章. 混凝土细观随机骨料结构与有限元网格剖分[J]. 计算力学学报, 2005, 22(6): 728-732. [8]WANG Z M, KWAN A K H,CHAN H C. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh[J]. Computers and Structures,1999, 70: 533-544. [9]刘瑜. 基于颗粒接触模型的砂土剪切波速研究[D]. 浙江杭州:浙江大学博士学位论文,2010. [10] 楚锡华. 颗粒材料的离散颗粒模型与离散-连续耦合模型及数值方法[D]. 辽宁大连: 大连理工大学博士学位论文,2006. [11] 秦建敏. 基于离散元模拟的岩土力学性能研究及应变局部化理论分析[D]. 辽宁大连: 大连理工大学博士学位论文,2007. [12] HANCHAK S J,FORRESTAL M J,YOUNG E R,et al. Perforation of concrete slabs with 48 MPa and 140 MPa unconfined compressive strengths[J]. International Journal of Impact Engineering, 1992, 12(1):1-7. [13] 张玲玲,姚勇. 四川西北地区砂卵石土的直剪试验研究[J]. 路基工程, 2010,(3):162-164.


2 砂卵石穿甲过程数值分析

2.1 穿甲过程分析

2.2 弹体的响应

2.3 墙体的响应

2.4 内部砂卵石土颗粒的响应

3 砂卵石颗粒级配对穿甲特性的影响





4 围压对穿甲特性的影响
5 结论
