一种基于密度的离群点检测方法
2018-04-11王向阳
王向阳
(陕西学前师范学院 陕西西安 710160)
离群点可理解为远离其他数据点或不服从基于多数样本数据建立的统计模型的数据[1]。尽管离群点在样本数据集中所占比例通常很小,但在某些领域内离群点检测工作却发挥着重要作用。例如在网络安全领域,异常的网络行为数据可能意味着网络入侵事件的发生。在电力行业,异常的用电行为数据可能意味着窃电现象或电力故障的发生。
目前基于密度的离群点检测方法比较流行,该方法的基本思想是从样本点所在空间的密度差异性来发现离群点。离群点从分布情况可分为全局和局部两类离群点。局部离群点相对全局离群点而言,更容易被聚类到某个类簇中,因此识别难度较大。针对局部离群点,研究者们基于离群点局部密度会低于其邻居点局部密度的假设,采用了诸如局部离群因子(local outlier factor, LOF)等评估策略来发现局部离群点[2-4]。例如Alex等在其提出的方法中假定离群点必须满足局部密度小、与高局部密度数据点的距离很远[5]。针对大规模的数据集而言,离群点检测的工作量大,时间效率低。对此,苟杰等先将数据集分割为互有重叠的子集,在子集中寻找K近邻并计算离群度,最后合并结果并遴选出离群点[6]。姜开元等通过R2-TREE的结构来提高数据检索效率,并借鉴LOF方法通过计算数据对象落在不同区域的概率来发现离群点[7]。针对高密度、多义性数据集,钱景辉将数据拆分成多示例包形式,运用退化策略及权重调整,计算离群点因子来判别离群点[8]。离群点的密度会受邻域划分程度及样本数据集稀疏性的影响,对此,王茜等鉴于近邻中不同的邻近程度发挥的作用不同,采用了基于链接的离群因子来解决离群点的密度与邻近点密度接近的情况[9]。Liu等[10]利用核K均值方法和核离群因子来计算每个样本数据认定为正例或负例样本的可能性,并基于支持向量数据描述来构建分类模型。Miao等[11]采用核局部离群因子来解决邻居点分布不均匀的情况。
由上述研究工作可见,检测局部离群点时需明确样本点的邻域,并考虑邻域内近邻点的分布情况及近邻点对目标样本点的影响。由于离群点并不一定是孤立的点,可能会与其同类的若干样本点紧密地聚集在其他类别样本的边缘地带,在该情况下将很难根据样本点与其邻近点的局部密度差异来发现离群点。在基于密度的聚类方法中,类簇间的边界地带是样本容易发生错误聚类的区域,显然从边界样本点出发寻找局部离群点会在一定程度上降低工作量。本文提出的方法首先利用有噪声的基于密度的聚类算法(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)[12]分离出明显不能划归到大类簇中的全局性离群点,然后根据小类簇中样本点的近邻关系(不考虑样本点所属类簇)和对小类簇局部密度的影响程度,来确定大类簇中应该划回小类簇的边界“错聚”样本点,最后以“错聚”样本点为参考对象筛选掉与其相距很远且局部密度高的邻居点,从而发现大类簇中“错聚”样本点邻域内的其他局部离群点。
1 基于密度的离群点检测
本文提出的方法主要由全局离群点提取、边界“错聚”样本点确定及局部离群点识别三部分组成。
1.1 全局离群点提取
DBSCAN算法可以将局部密度大且相连的区域内的样本点聚集到一起形成类簇,其对噪音点和异常点具有很强的免疫能力。其核心思想是找到满足半径Eps内邻居样本数不少于minPts的核心点,并以每个核心点代表一个区域,将相距不超过Eps的核心点所代表的区域进行合并。其缺点是由于密度连通关系的传递性会使大多数样本点聚集到非常少的类簇中[11]。本文提出的方法将DBSCAN算法聚类出的小类簇和噪音点作为全局离群点。
1.2 边界“错聚”样本点确定
在不考虑样本点归属的情况,本文提出的方法先依据欧式距离确定每个小类簇中样本点在一定半径内的k个近邻,然后标记k个近邻中位于大类簇中的样本点,从而确定边界区域“错聚点”候选集合。若候选样本点属于“错聚点”,则将其划归回相应的类簇后,类簇的局部密度应该变得紧密,至少不会变得稀疏。LOF是比较流行的度量样本点与其邻居点局部密度差异的方法。样本点q的LOF评估公式如下[2]:
(1)
(2)
reach-distk(q,p)=max{d(q,p),k(p)}
(3)
式中,Nk(q)为样本点q的k个近邻,Lrdk(q)为样本点q的局部可达密度,reach-distk(q,p)为样本点q相对其近邻点p的可达距离,d(q,p)为样本点q和p间的距离,k(p)为样本点p到距离其最近的第k个近邻点的距离。若样本点不是离群点,则其LOF值应在0至1之间。基于LOF的度量方法,本文度量候选样本点q对类簇Ci的贡献程度公式为:
(1-LOFk(pj))×α
(4)

1.3 局部离群点识别
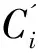
(5)
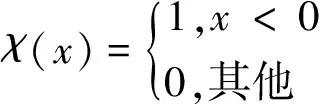
(6)
式中,distc为检索半径。样本点xi到高密度样本点的距离计算公式为[3]:
(7)

(8)
(9)

2 实验
实验采用UCI提供的shuttle数据集[13]来验证离群点检测方法的检测效果。shuttle数据集由7个类别样本组成,包含了43 500个训练样本和14 500个测试样本,其中每个样本由7个数值型属性组成。实验去掉shuttle数据集中第4类样本,选取第1类作为正例样本,其余类别作为负例样本(离群点)。处理后正例样本数为45 586,离群点数为3 511。实验首先采用z-score公式对样本数据进行标准化处理[14]:
(10)
式中,μ为属性值的均值,σ为属性值的标准差。为检测全局离群点,DBSCAN方法的半径Eps取值为0.1,最小样本数minPts取值为100,聚类结果如表1所示。

表1 DBSCAN聚类结果Table 1 DBSCAN clustering results
针对类簇2和类簇3,实验采用公式(4)确定各自在类簇1中的边界“错聚”样本点,其中公式(4)的调整因子α取值为10。确定边界“错聚”样本点后,实验将每个“错聚”样本的邻域半径设定为0.5,并采用公式(8)来确定类簇1中的局部离群点,公式(8)中调整因子β取值为10。公式(4)中样本点近邻数k的取值和依据公式(8)计算样本点偏离度的阈值TH都会对局部离群点检测造成影响。图1和图2为近邻数k和偏离度阈值TH调整时,类簇1中局部离群点检测方法的查全率和查准率。图1中参数TH调整时局部离群点的查全率变化不大,但对应的查准率变化却非常大,可见k取值为15和偏离度阈值TH取值为5时方法的局部离群点检测效果较好。

图1 参数调整时大类簇中局部离群点的查全率Fig.1 The recall rate of local outliers in thelarge group clusters when the parameters are adjusted

图2 参数调整时大类簇中局部离群点的查准率Fig.2 The precision rate of local outliers in thelarge group clusters when the parameters are adjusted
如何确定样本点的局部邻域及如何度量样本点的离群程度是每个离群点检测模型都要解决的问题,因此当大量的参数需要进行调整时检测模型的性能将受到极大的影响。Alex等[5]提出的离群点检测方法(简记为快速法)仅需考虑样本点的局部密度及到高密度点的距离,因此执行速度非常快。实验观察了该方法在shuttle数据集上的检测效果。实验过程如下:(1)利用公式(5)计算每个样本点的局部密度,公式(5)中的检索半径设定为0.5;(2)按密度值降序排列得到高密度的100个样本点和低密度的5 000个样本点;(3)利用公式(7)计算每个低密度的样本点到高密度样本点的距离,按距离值降序排列后输出前3 500个样本点。实验发现当快速法保持低密度样本点总数不变,高密度点总数取200,500及1 000时离群点的检测结果无变化,可见快速法适合检测全局离群点。两种离群点检测方法的检测结果对比如表2所示。从表2可以看出,虽然本文提出的方法比较复杂,但能在保障查准率的前提下检测出更多的离群点。

表2 离群点检测结果比较Table 2 Comparison of outlier detection results
3 结束语
本文提出了一种基于密度的离群点检测方法,该方法首先从全局角度分割样本特征空间中密度不一致且不连通的样本区域,以便识别出全局离群点,然后从局部角度识别出边界区域内被错误聚类的离群点,进而发现更大范围内的局部离群点。实验结果证明了提出的方法的可行性和有效性。但本文方法并未考虑高维特征时模型的优化问题,同时也未考虑样本点聚类后离群点远离类簇间边界的情况,需要进一步研究。
[1]范小刚.基于k近邻树的离群检测算法研究[D].重庆:重庆大学,2014.
[2]王敬华,赵新想,张国燕,等.NLOF:一种新的基于密度的局部离群点检测算法[J].计算机科学,2013,40(8):181-185.
[3]LIU J, DENG H F. Outlier detection on uncertain data based on local information[J]. Knowledge-Based Systems, 2013, 51(1):60-71.
[4]邹云峰,张昕,宋世渊,等. 基于局部密度的快速离群点检测算法[J].计算机应用,2017,37(10):2932- 2937.
[5]ALEX R, ALESSANDRO L. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191):1492-1496.
[6]苟杰,马自堂,张喆程. PODKNN:面向大数据集的并行离群点检测算法[J]. 计算机科学,2016,43(7):251-254,274.
[7]姜元凯,郑洪源,丁秋林.一种基于密度的不确定数据离群点检测算法[J].计算机科学,2015,42(4):172-176.
[8]钱景辉,梁栋.一种基于多标记的局部离群点检测算法[J]. 微电子学与计算机,2017, 34(10):110-114.
[9]王茜,刘书志.基于密度的局部离群数据挖掘方法的改进[J].计算机应用研究,2014, 31(6):1693-1696.
[10] LIU B, XIAO Y, YU P S, et al. An efficient approach for outlier detection with imperfect data labels[J]. IEEE Transactions on Knowledge & Data Engineer,2014, 26(7):1602-1616.
[11] MIAO D, QIN X, WANG W. Anomalous cell detection with kernel density-based local outlier factor[J]. Communications China, 2015, 12(9):64-75.
[12] KALIFA M B, REDONDO R P D, VILAS A F, et al. Is there a crowd? experiences in using density-based clustering and outlier detection[C]. Proceedings of the 2nd International Conference on Mining Intelligence and Knowledge Exploration,2014,8891:155-163.
[13] UCI shuttle data[DB/OL]. http://archive.ics.uci.edu/ml/datasets/Statlog+(Shuttle).
[14] 薛安荣,刘彬,闻丹丹.基于小波变换的分布式隐私保护聚类算法[J].计算机应用,2014,34(4):1029-1033.
