基材的应变强化效应对蜂窝缓冲性能的影响

孙德强， 张志娟

(陕西科技大学 轻工科学与工程学院， 陕西 西安　710021)

0　引言

蜂窝材料具有较高的比强度和比刚度，能够在发生大变形时吸收大量能量，优良的力学性能使其被广泛应用于航空航天、汽车和包装工程等领域[1].随着蜂窝材料应用范围的不断扩展，与其相关的研究也不断深入.文献[1]和[2]对多孔固体的结构和性能以及在工程设计中的利用方法等做了全面的论述.Mahmoudabadi等[3]结合理论与实验研究了六边形金属蜂窝在类静态低速冲击下的力学行为和能量吸收.孙德强等[4,5]通过模拟试验载荷条件的方法，精确推导了双壁厚蜂窝铝芯的共面弹性模量，并给出了其静态峰应力、密实化应变和单位体积密实化应变能的计算公式.文献[6]采用显示动力有限元方法研究了胞元构形、冲击速度以及相对密度等因素对铝蜂窝动态力学性能的影响.上述研究为蜂窝材料的研究提供了可靠的理论依据，但是关于基体材料的力学性能产生的影响并未涉及.大多数工程材料在初始屈服之后都会呈现应变强化[7]，Liu等[8,9]对四种基材模型的金属泡沫进行冲击载荷下的仿真模拟，该研究证明基材的应变强化效应会对蜂窝材料的力学性能产生一定影响，具体的影响规律还需进一步探究.

目前，二维多孔材料的力学行为分析多采用有限元方法.传统的实验方法虽然同样能得到可靠的数据和结果，但是试验量庞大，不同材料参数的试样难以收集并且无法保证本研究中样品结构参数保持一致的需求.Ruan等[10]、Zheng等[11]、Ali等[12]、孙德强等[13]基于有限元分析软件对二维多孔材料的力学行为进行了大量的模拟仿真计算，并验证了所建模型的可靠性，本文将基于这些研究模型，以正六边形蜂窝为例，采用有限元法来研究基材的应变强化效应对蜂窝共面缓冲性能的影响.

1　有限元模型与数据分析方法

1.1有限元模型

参考文献[10-13]中的有限元模型，在ANSYS/LS-DYNA软件中建立的正六边形蜂窝共面冲击有限元计算模型，如图1所示.蜂窝样品放置在水平设置的上压板和固定支撑板之间，x1和x2皆为蜂窝的共面方向，垂直于x1x2平面为异面方向.上压板和支撑板定义为无任何变形的刚体，支撑板固定，使上压板以恒定的加载速度沿x1方向向下运动向蜂窝样品施加载荷.在建立仿真模型中假设样件为完全规则的正六边形结构，材料为无裂纹、孔洞及各种初始缺陷的理想材料，整个模型单面无摩擦自动接触，设定样件与上压板和固定支撑板之间存在摩擦力，摩擦系数都为0.02，样品异面方向位移约束为0.采用4节点壳单元Shell163对模型进行网格划分，有限单元边长为0.5 mm.蜂窝样品单元数量为15×15，正六边形胞元的结构参数恒定，其边长l=3 mm，胞壁厚度t=0.1 mm，样品沿异面方向的厚度b=10 mm。基体材料为双线性应变硬化材料，其相关力学参数为：密度ρ=2 700 kg/m3，杨氏模量E=70 Gpa，屈服应力σy=292 MPa，泊松比v=0.35.

另外，模型中基体材料指定双线性应变强化材料模型，其应力σ和应变ε关系式如下[14]：

σ=Eε0≤ε≤εy

σy+ET(ε-εy)εy≤ε≤εf

(1)

式(1)中：σy是屈服应力；εy是屈服应变；ET是塑性强化模量，为了方便起见，本文采用塑形系数(=ET/E)作为材料强化参数[15]，分别取0、 0.01、 0.03、 0.05、 0.07、 0.09和0.1,当=0时，即表示材料为弹性理想塑性材料，其余均为弹性-线性应变强化材料.

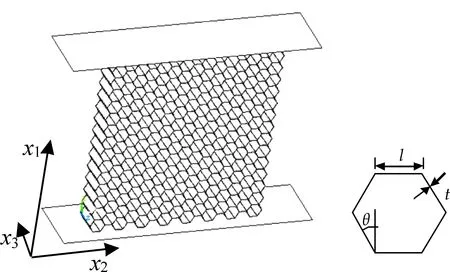
图1　正六边形蜂窝芯材共面冲击有限元模型

1.2　数据分析方法

利用所建立的有限元模型进行大量的模拟计算后，将所得数据用后处理软件LSPREPOSTED直接得出上压板与样品间沿压缩方向的作用力与时间曲线F-t和位移与时间曲线u-t，通过变换坐标轴获得F-u曲线；利用式(2)和F-u曲线可以得到σ-ε曲线 .

σ=F/A,ε=u/h

(2)

式(2)中：σ、ε为样品关于压缩作用力F的应力、应变；A为沿x1方向上样品的横截面积；h为样品沿x1方向上的长度.

利用LSPREPOSTED软件还可直接获得样品动能与时间曲线K-t、内能与时间曲线I-t、总能量吸收与时间曲线E-t，处理后最终得到动能、内能、总能量吸收与应变的曲线K-ε、I-ε、E-ε.

以上曲线此处不列出讨论，蜂窝样品σ-ε曲线和总能量吸收曲线E-ε将在下文作详细分析.

2　结果与讨论

2.1变形模式

不同的冲击速度下，正六边形蜂窝表现出不同的变形模式，表1列出了当ε=0.2，分别为0、0.05、0.1时，蜂窝样品在不同冲击速度下的变形图.从图可以看出,低速下(v=3 m/s)，样品出现“X”型局部变形带，随着值得增大，处于X变形带上的胞元局部坍塌程度减小，胞元完整性更高，并且局部变形弥散到更多的胞元，当=0.05时，上压板和支撑板附近都出现了X型变形带，而当=0.1时，已不能明显观察到X型变形带，只有靠近上下刚板的胞元发生了坍塌；中速下(v=30 m/s)，出现了开口朝上的“V”型局部变形带；高速冲击下(v=30 m/s)，样品呈“一”字型坍塌.

班干部选拔制度不科学也是班级管理制度不完善的重要表现。班干部选拔主要有任命、轮值、选举三种方式。这三种方式都看重学生的道德品质、学习成绩与能力素质，又都有各自的特点和适用的条件。许多班主任往往忽视了班级的具体情况，不能结合实际选拔班干部。比如，有的班主任为了省事省力，往往采取直接任命的方式确定班干部人选，摒弃轮值和选举的方式，难以激发大学生参与班级自主管理的积极性和主观能动性。由于缺乏参与意识和锻炼机会，班级大部分学生对班级管理漠不关心，班级管理不得不回归传统管理的老路。

表1　=0，=0.05，=0.1时蜂窝芯材在不同冲击速度下ε=0.2 时的变形模式图

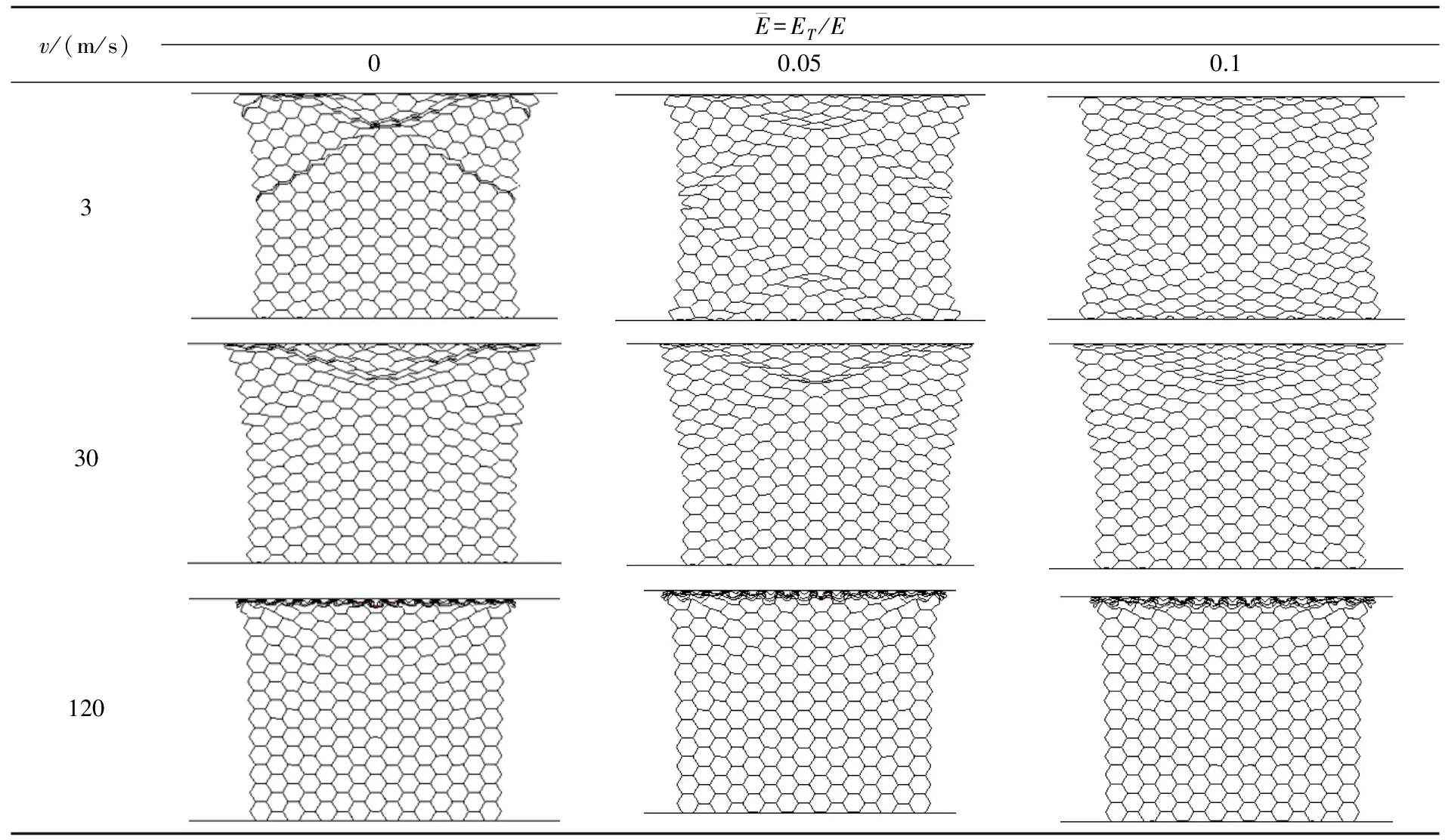
表1　=0，=0.05，=0.1时蜂窝芯材在不同冲击速度下ε=0.2 时的变形模式图

v/(m/s)E=ET/E00．050．1330120

2.2　动态峰应力

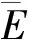
图分别为0,0.05,0.1时蜂窝芯材共面冲击应力-应变曲线

根据平台区的动态峰应力公式(3)，可计算得到不同加载速度(分别为3、10、30、50、70、90和120 m/s)下样品的动态峰应力，如表2所示.

(3)

式(3)中：σp为蜂窝动态峰应力；ε0为初始应变；εD为密实化应变.

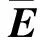
表2　不同值的正六边形蜂窝在不同冲击速度下的动态峰应力　　　　　　MPa

σp=σp0+Av2

(4)

式(4)中：σp为蜂窝的动态峰应力；σp0为静态峰应力；A关系系数 ；v为加载速度.

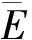
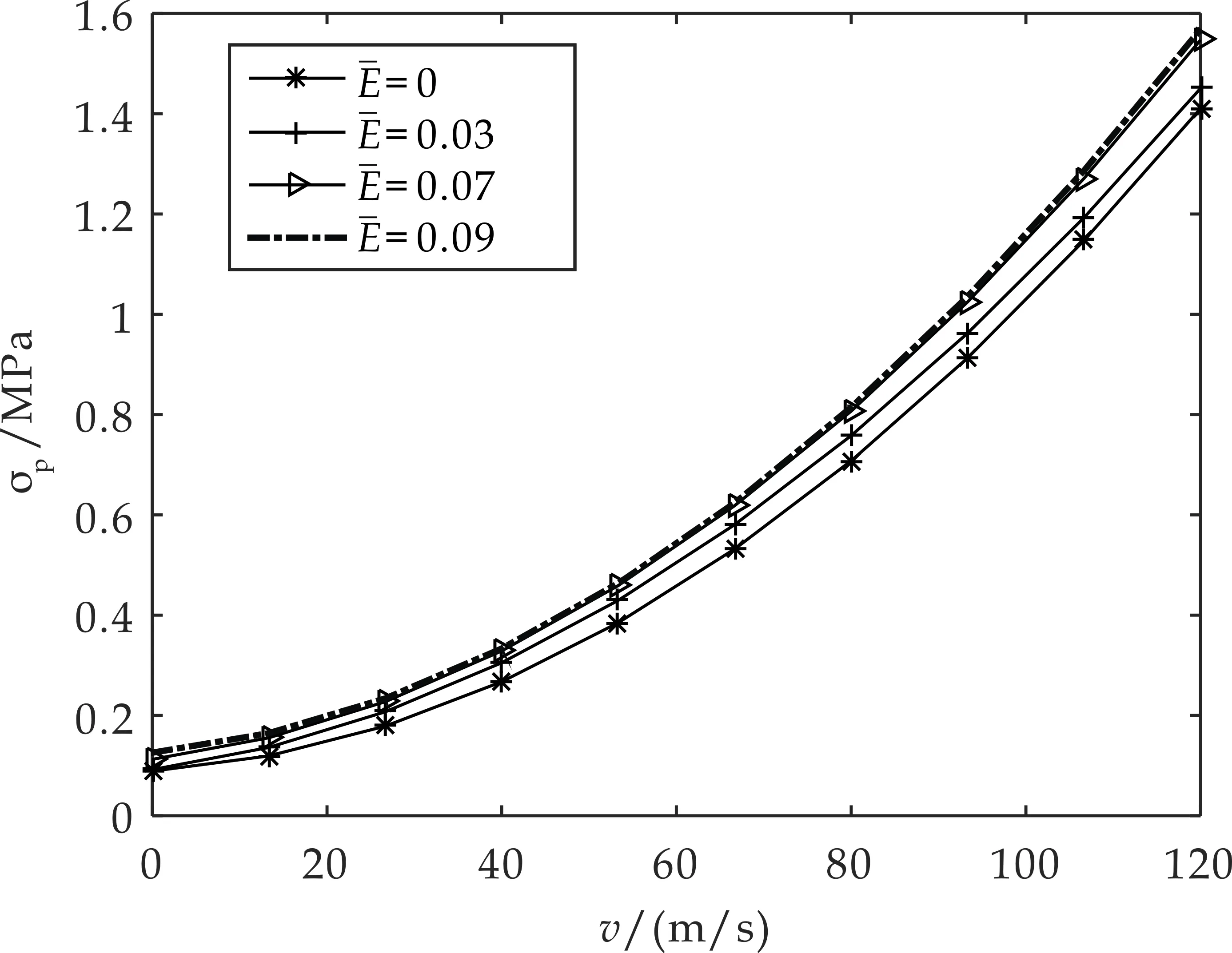
图3　动态峰应力-冲击速度拟合曲线

为了进一步讨论基体材料对蜂窝共面冲击响应的影响，定义λ来表示与弹性理想塑性材料相比较，弹-线性强化材料引起的蜂窝动态峰应力的相对增长.

λ=(σ弹-线性强化-σ0)/σ0

(5)

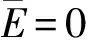
表3　动态峰应力的相对增加量λ

2.3　能量吸收

3　结论

为了研究基体材料的应变强化效应对蜂窝力学性能的影响，对结构参数完全相同而基体材料分别为弹性理想塑性材料和弹性-线性应变强化材料的正六边形蜂窝进行共面冲击载荷下的模拟仿真，获得各自的变形模式图，并对仿真数据进行后处理获得应力应变曲线，动态峰应力以及能量吸收图.分析讨论以上结果，得到如下结论：

(1)材料的应变强化效应能够使蜂窝整体变形趋于均匀化，但对变形模式的类型影响不大，变形模式主要决定于加载速度的大小.

(2)材料的应变强化效应能够引起正六边形蜂窝动态峰应力和总能量吸收的增长，尤其在低速冲击下，能够有效提高蜂窝的缓冲性能，但这种增长趋势随着加载速度的增加逐渐减弱.

[1] Gibson L J,Ashby M F.Cellular solids:Structure and properties[M].2nd.London:Cambridge University Press,1997.

[2] 孙德强.多孔缓冲材料有限元结构分析与设计方法[M].北京:化学工业出版社,2014.

[3] Mahmoudabadi M Z,Sadighi M.A theoretical and experimental study on metal hexagonal honeycomb crushing under quasi-static and low velocity impact loading[J].Materials Science & Engineering A,2011,528(15):4 958-4 966.

[4] 孙德强,张卫红,孙玉瑾,等.蜂窝铝芯的弹性模量和材料效率分析[J].力学与实践,2008,30(1):35-40.

[5] 孙德强,高田莉,王庆庆,等.一种确定六边形蜂窝芯材共异面弹性模量的简单有限元法[J].陕西科技大学学报(自然科学版),2014,32(2):130-133.

[6] 胡玲玲,蒋玲.胞孔构型对金属蜂窝动态力学性能的影响机理[J].爆炸与冲击,2014,34(1):41-46.

[7] 余同希.塑性结构的动力学模型[M].北京:北京大学出版社,2002.

[8] Liu Y D,Yu J L,Zheng Z J,et al.A numerical study on the rate sensitivity of cellular metals[J].International Journal of Solids & Structures,2009,46(22-23):3 988-3 998.

[9] 刘耀东.多孔金属材料率效应的数值分析与动态压缩行为的理论研究[D].安徽:中国科学技术大学,2010.

[10] Ruan D,Lu G,Wang B，et al.In-plane dynamic crushing of honeycombs-a finite element study[J].International Journal of Impact Engineering,2003,28(2):161-182.

[11] Zheng Z,YU J,LI J.Dynamic crushing of 2D cellular structures:A finite element study[J].International Journal of Impact Engineering,2005,32(1):650-664.

[12] Ali M,Qamhiyah A,Flugrad D,et al.Theoretical and finite element study of a compact energy absorber[J].Advances in Engineering Software,2008,39(2):95-106.

[13] Sun D,Zhang W.Mean in-plane plateau stresses of hexagonal honeycomb cores under impact loadings[J].Composite Structures,2009,91(2):168-185.

[14] 余同希,卢国兴,华云龙.材料与结构的能量吸收:耐撞性包装安全防护[M].北京：化学工业出版社,2006.

[15] Mousanezhad D,Ghosh R,Ajdari A,et al.Impact resistance and energy absorption of regular and functionally graded hexagonal honeycombs with cell wall material strain hardening[J].International Journal of Mechanical Sciences,2014,89:413-422.

[16] Reid S R,Peng C.Dynamic uniaxial crushing of wood[J].International Journal of Impact Engineering,1997,19(5-6):531-570.