中国股市动量和反转策略的尾部风险分析
2018-04-11王小华
王小华,刘 阳,黄 卓
(1.中央财经大学 中国经济与管理研究院,北京 100871;2.中国国际金融有限公司,北京 100004;3.北京大学 国家发展研究院,北京 100871)
0 引言
金融市场有效市场假说认为,市场中的所有相关信息均能够在证券价格中充分及时地体现出来,投资者只能获得风险调整后的平均收益[1]。自20世纪80年代以来,学者们发现了许多市场异象[2],对有效市场假说提出了挑战,其中一个著名的异象就是股票价格的动量效应[3]和反转效应[4]。动量效应是指收益率会延续原来的运动方向,过去收益率较高的投资组合在未来仍会获得较高收益,而过去收益率较低的投资组合在未来获得较低收益。反转效应则正好相反。基于上述两种效应,投资者可以仅依据股票过去一段时间的收益状况建立投资策略获取超额收益,这显然违背了有效市场假说。由于动量和反转效应针对的信息集仅包括价格序列,从而对最容易被人接受的弱有效市场假说构成了挑战。
我国目前对于动量和反转效应的研究大多参照国外的方法使用中国市场数据进行实证研究。由于采用了不同的研究时间、数据频率以及对数据的处理方法,因此所得到的结果也不相同。例如在月度频率上,王永宏和赵学军(2001)[5]发现了收益反转的特征,但是朱战宇等(2003)[6]则没有发现这种效应,而鲁臻和邹恒甫(2007)[7]则发现了动量效应。近两年开始有学者关注动量和反转策略的尾部风险问题。Daniel(2011)[8]发现美国市场动量收益最低的时候大都发生在过去两年市场低迷的时候,尤其是当经济出现严重危机导致市场大幅下跌时。当市场处于熊市,波动率又很大的时候,原有的动量收益出现了反转,作者将其称之为“Momentum Crash”。Daniel(2012)[9]提出了一个马尔科夫模型来捕捉历史收益率和当期收益率对于动量策略的影响,发现动量策略下的极端损失更容易发生在市场动荡期当中。本文借鉴了Daniel(2012)[9]提出的一个包含平静状态和动荡状态的两个隐性状态的马尔科夫模型,用来刻画持有期1周的短期动量策略收益率的动态过程,并且基于该模型对动量策略的尾部风险进行了研究。
1 数据和方法
相较于发达国家,国内股票市场发展时间较短,偏好短期交易的个人投资者占比较高,因此本文采用周度频率数据作为研究对象。所有数据均来自于RESSET金融研究数据库。在个股与市场收益率方面,本文选取的时间区间从1995年1月开始,到2012年9月为止,所有个股均采用RESSET股票综合数据库中按分红情况调整后的收益率。本文剔除了每只股票最初30个交易周的交易数据,同时还剔除了过去1年当中交易周数小于30周的股票。
本文沿袭了Jegadeesh和Titman(1993)[3]的方法,定义某一周之前的J周(含当周)为形成期,该周之后的K周为持有期。在本文当中,J和K取值为1、2、3、4、12、26和52,两两组合形成49种策略,其中4周以内的策略用于考察短期的周度动量和反转现象,4周及4周以上的策略用于考察中长期的月度动量和反转现象。对于每一种策略,以形成期周均收益率在前20%的股票为赢者组合,后20%的股票为输者组合,动量策略组合定义为做多赢者组合同时做空输者组合,如果在持有期当中,动量策略组合的收益率显著大于零,则说明国内股市存在动量效应,反之则存在反转效应。
在尾部风险的分析方面,本文采用了Daniel等(2012)[9]提出的模型之一,把历史收益率的变动用一个隐性的马尔科夫过程进行描述,然后将其添加到动量策略收益与当期收益率的模型当中,来综合考察市场历史状况和当期市场涨跌对动量策略组合收益的影响。
定义St为第t期时的市场状态,st为这一状态的实现值。本文假设市场只存在两种状态:平静C和动荡T。这两种状态本身是不可观测的,但是在每一期,市场处于平静期还是动荡期会存在一个概率,并且这两种状态之间存在着一个稳定的转移概率,使得市场在这两种状态之间进行转换。

动量策略组合和市场组合的收益率以及波动率都是市场状态的函数,于是动量策略组合的收益率可以写成如下形式:分别服从独立同分布的标准正态分布,σmom、σM分别代表动量策略组合的残差收益的波动率。虚拟变量Iupt取1时,代表与动量组合同一周的市场收益率为正。
根据上述模型的构造过程,该模型的待估计参数组合θ主要包括以下14个参数:
市场处于平静期时:
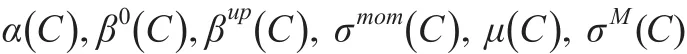
市场处于动荡期时:
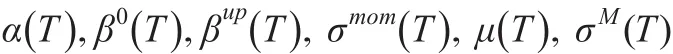
市场状态的转移概率:

用来估计上述参数使用到的数据主要包括三个序列:动量策略组合的收益率、市场收益率以及利用市场收益构造的虚拟变量。为了估计上述参数,本文采用极大似然估计的方法,为此需要构造似然函数。
每一期市场中可以观察到的变量就是估计参数时需要的三个变量:和,定义yt为上述三个变量的组合。每一期市场历史的信息集Ft-1包含了过去全部可观察的变量,即
下面给出似然函数的迭代过程:

其中,给定当期市场状态St=st和历史信息集Ft-1,yt的概率密度函数的形式为:

根据对动量策略组合收益率和市场收益率的构造定义:
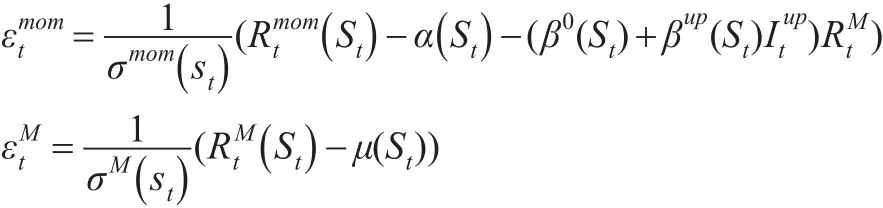
给定历史信息集Ft-1,当期市场状态St=st的概率为:

在式(2)最后一步推导过程当中,Pr(St=st|St-1=T)和Pr(St=st|St-1=C)是待估计的转移概率,而后面的两个分式的分子和分母则分别与式(1)中的Pr(yt|Ft-1)、Pr(yt,St=C|Ft-1)和Pr(yt,St=T|Ft-1)三项形成了迭代关系,至此,整个条件极大似然函数的迭代过程计算完毕。
为了估计参数θ,需要最大化对数似然函数:
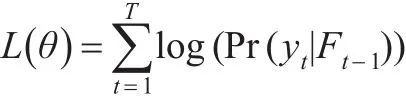
最后,本文还考察了市场状态与尾部风险之间的关系。尽管每一期平静和动荡两种状态无法通过参数估计的结果进行准确划分,但是基于历史信息集,每一期市场处于两种状态的概率却可以计算出来,作为衡量市场状态的重要指标。在计算状态概率时,本文使用了样本内和样本外两种方法。样本内方法是使用全部可得的动量策略组合和市场组合收益率估计模型参数,然后根据模型的迭代关系和收益率数据计算各期的状态概率。样本外的方法在模型参数估计以及计算状态概率时,仅使用了当期之前的全部收益率数据,因此有效地避免了样本内计算的问题。本文在实际计算时,采用了不同持有期和形成期策略下最后400个周作为样本外预测的观察区间。
2 实证结果及分析
2.1 国内股票市场动量反转策略的表现
下页表1整理了49组不同形成期和持有期策略下动量策略组合的收益情况,表格中的均值为周度收益,单位为10-2。在全部49种策略当中,有40个组合的收益率为负值,其中有13个组合的收益率在5%的显著性水平下显著为负。具体来看,反转效应的强弱与持有期存在比较明显的关系。持有期在半年以上的14种组合周均收益均在-0.1%以上,并且反转效应均不显著,有5个组合还体现出了微弱的动量效应。在持有期为1周的组合反转效应体现得最为明显,反转收益的极值出现在持有期和形成期均为1周的超短期组合,周均收益为-0.53%。
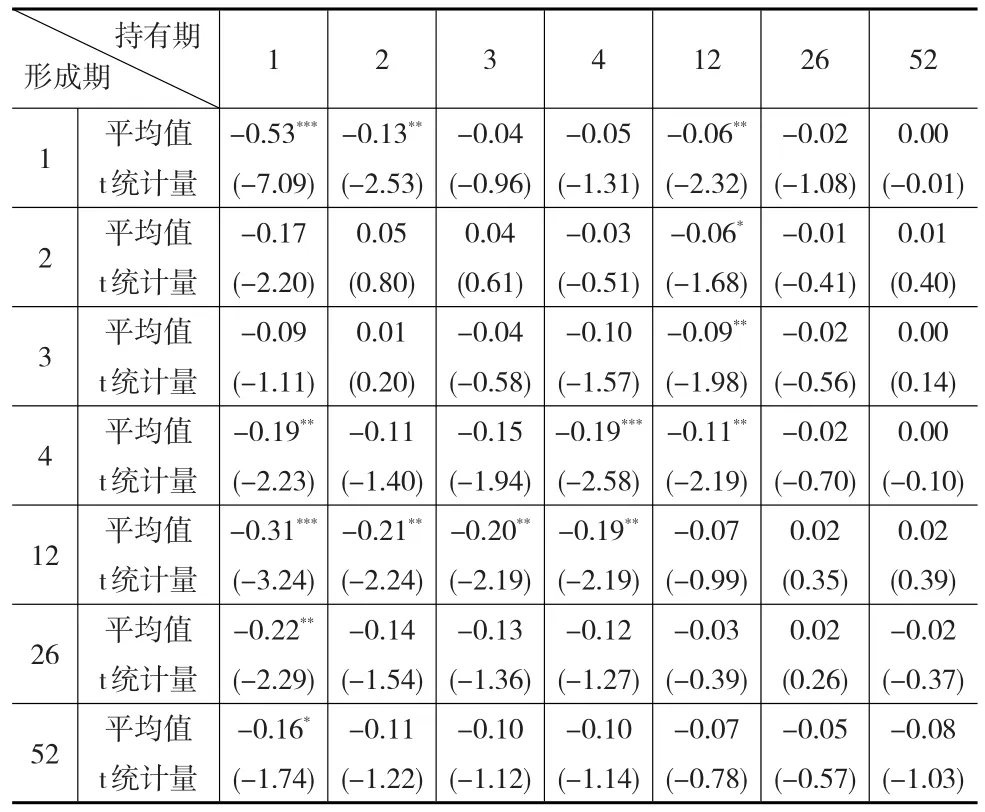
表1 49种动量策略组合收益率
2.2 动量策略的尾部风险
根据上文对于国内动量策略收益率的实证结果,在持有期为1周的组合反转效应体现得最为明显,因此本文将研究的重点放在持有期为1周的7种策略上。
表2给出了持有期为1周的7种动量策略收益率的描述性统计量的情况。7种策略的平均收益率均在0~1%之间,波动率在3%以内。从偏度的角度看,形成期在1个月及1个月以内的策略具有较高的正偏度,这说明右边的尾部相对于左边的尾部要长。从极值来看,动量策略组合单周的最大收益均超过了10%,其中形成期26周的策略最高,达到15.06%,单周最大跌幅也均在9%以上,其中形成期52周的策略的单周最大跌幅达到17.29%,这些极端收益的存在表明动量策略本身有一定的尾部风险。

表2 动量策略周度收益的描述性统计
从表2提供的峰度数值来看,全部7种策略均具有较高的峰度,这说明动量策略的收益率具有厚尾效应。表3则将这种尾部风险与正态分布进行了详细的比较。如果动量策略的周度收益服从正态分布,那么持有期在4周和4周以下的4种策略单周收益率的绝对值超过9%的概率均在万分之一左右,也就是说,在样本个数均少于900周的情况下,单周收益率的绝对值超过9%的样本数量应趋近于零,但实际情况却并非如此。4种策略下均存在单周收益率的绝对值超过9%的样本,形成期3周的策略单周收益率超过9%的样本数达到了3个,持有期在4周以上的3种策略也同样存在着超出正态分布水平的极端收益。这进一步印证了动量策略尾部风险的存在性。

表3 动量策略周度收益的尾部风险
2.3 马尔科夫模型的实证结果
表4给出了马尔科夫模型的极大似然估计结果,其中α、σmom、μ和σM四个参数估计值的单位为10-2,转移概率指当期状态延续到下一期相同状态时的概率,括号中的数值为参数的t统计量。
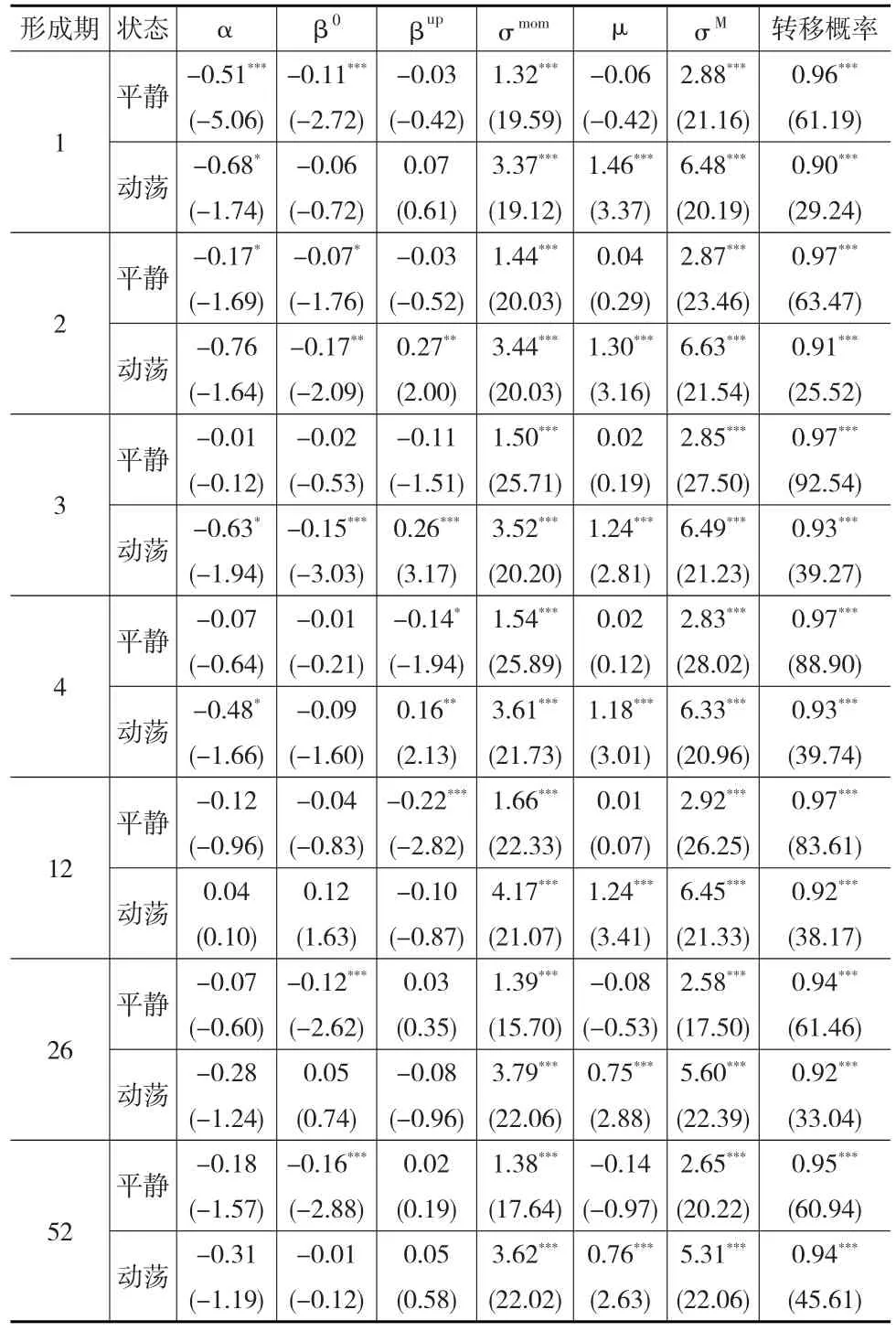
表4 马尔科夫模型参数估计
市场状态的特征体现在动量策略组合以及市场组合的波动率上,在全部7种持有期下,两种市场状态下的波动率均非常显著,动荡期的波动率要大于平静期。市场状态的动态演变过程体现在相邻两期相同状态的转移概率上。两个转移概率均超过90%,体现了动荡状态和平静状态都具有良好的持续性。市场状态的这种延续性说明他们相较于股票的价格和收益率更容易预测,这为马尔科夫模型的样本外预测奠定了基础。此外,对于平静期而言,状态延续的概率要高于动荡期,这说明平静状态比动荡状态更加稳定。
虽然每一期的市场状态的实现值无法观察,但是通过模型估计的参数和历史收益率数据可以计算给定历史信息集,每一期市场处于这两种状态的概率。若将市场处在平静状态的概率超过50%的时期定义为平静期,而将市场处在动荡状态的概率超过50%的时期定义为动荡期,表5则分别汇总了两种市场状态下动量策略收益率以及处于动荡期和平静期的天数。在全部7种策略下,动荡期的天数都少于平静期,这与相邻两期相同状态的转移概率的结果保持一致:平静状态延续到下期的概率比动荡状态更高,从而使得平静状态概率超过50%的天数更多。而从平静期和动荡期动量策略收益率的描述性统计量来看,动荡期的动量策略的收益率均低于平静期,但是波动率却要高于平静期。

表5 两种市场状态下的动量策略收益率
2.4 马尔科夫模型市场状态与动量策略的尾部风险
本文采用了样本内和样本外两种方法计算了每一期市场处于两种状态的概率,并且考察了动量策略尾部风险和市场状态之间的关系。无论在样本内还是样本外,动量策略的极端收益发生在马尔科夫模型计算的动荡期的概率更高,马尔科夫模型刻画的市场状态可以较好地捕捉动量策略的尾部风险。在不同形成期的7种策略体现的结果较为一致,因此本文以形成期4周的策略为例介绍了主要的结果和结论,并把其他策略的结果放在最后作为参考。


图1 动荡状态概率与动量策略组合收益率的散点图(形成期4周)
图1分别给出了形成期4周的动量策略用样本内方法和样本外方法计算的市场状态概率与当期动量策略收益率之间的散点图。
表6和表7则分别统计了样本内和样本外方法计算的动荡状态概率超过一定临界值时对动量策略的极端损失和收益的覆盖情况。表6和表7当中的第一列是给定历史信息集,动荡状态概率的临界值,以10%作为步长,第二列则是动荡状态概率超过给定临界值时的样本周数,表格的第二行给出了极端损失或者极端收益的临界值,以收益率的绝对值超过5%为限,以1%为步长。表格内其他行列交叉点表格中数字的分母部分为动量策略收益率超过给定临界值的样本个数,分子部分为这种样本落在动荡期的样本个数。

表6 动荡状态概率与动量策略组合极端收益率(样本内,形成期4周)

表7 动荡状态概率与动量策略组合极端收益率(样本外,形成期4周)
在表6中,以动荡状态超过50%定义为动荡期,极端损失落在动荡期的概率最小值为78.9%(15/19,收益率低于-5%),而且随着极端损失临界值的降低,极端损失落在动荡期的概率越来越高,而动量策略收益率低于-8%的3个样本不仅全部落在了动荡期,而且处在动荡状态的概率全部超过了90%。极端收益落在动荡期的概率最小值为77.8%(14/18,收益率高于5%)。动量策略收益率超过9%的2个样本全部落在了动荡期,而且处在动荡状态的概率均超过了90%,但动量策略收益率超过8%的10个样本当中只有8个样本落在了动荡期,也只有5个样本处在动荡状态的概率超过了90%。相同收益率临界值情况下,极端收益落在动荡状态概率超过50%和90%的概率,均没有超过极端损失落在相同条件下的概率,也就是说,马尔科夫模型定义的动荡状态对于极端损失的覆盖效果更好。
从表7来看,采用样本外方法计算的动荡期对于极端损失和收益的覆盖效果比样本内的结果要差,但是仍然至少覆盖了66.7%的尾部风险。极端损失落在动荡期的概率最小值为50%,动量策略收益率低于-7%的4个样本仅有2个样本处在动荡状态的概率超过了90%。在表7中,极端收益的结果与极端损失的结果类似。极端损失落在动荡期的概率最小值为66.7%。动量策略收益率超过8%的3个样本中有2个样本落在了动荡期,并且这2个样本处在动荡状态的概率均超过了80%,但没有达到90%。在样本外方法下,马尔科夫模型定义的动荡状态对于极端损失的覆盖效果也要优于极端收益。
3 结论
本文沿用了Jegadeesh和Titman(1993)[3]提出的对于动量效应的研究方法,利用国内股票市场的1995年1月到2012年9月的周度交易数据,研究了国内股市的动量效应。中国股票市场整体上体现为反转效应,做多输者组合,做空赢者组合的反转策略多数情况下可以获得正回报,动量效应体现得比较微弱。在国内采用动量和反转策略在收益和损失两个方向上均存在一定的尾部风险,而且这种尾部风险存在于多种形成期的策略之下。为了对这种尾部风险进行分析,本文采用了一个包含平静状态和动荡状态的两个隐性状态的马尔科夫模型,用来刻画持有期1周的动量组合收益率的动态过程。本文的实证结果表明,极端收益和损失更容易发生在市场处在动荡状态的情况下,在平静状态下出现尾部风险的概率较低。这在一定程度上对动量策略的尾部风险进行了解释。
参考文献:
[1]Fama E F.Efficient Capital Markets:A Review of Theory and Empirical Work[J].Journal of Finance,1970,25(2).
[2]Banz,Rolf W.The Relationship Between Return and Market Value of Common Stocks[J].Journal of Finance Economics,1981,(9).
[3]Jegadeesh N,Titman S.Returns to Buying Winners and Selling Losers:Implications for Stock Market Efficiency[J].The Journal of Finance,1993,48(1).
[4]DeBondt W F M,Thaler R.Does the Stock Market Overreact?[J].The Journal of Finance,1985,40(3).
[5]王永宏,赵学军.中国股市“惯性策略”和“反转策略”的实证分析[J].经济研究,2001,(6).
[6]朱战宇,吴冲锋,王承炜.不同检验周期下中国股市价格动量的盈利性研究[J].世界经济,2003,8(8).
[7]鲁臻,邹恒甫.中国股市的惯性与反转效应研究[J].经济研究,2007,9(13).
[8]Daniel K.Momentum crashes[J].Columbia Business School Research Paper,2011,11(3).
[9]Daniel K,Jagannathan R,Kim S.Tail Risk in Momentum Strategy Returns[R].National Bureau of Economic Research,2012.
