表面处理对柔轮材料力学性能影响的有限元分析

祝晋旋，王家序, 2，周青华，周博，龙见炳



表面处理对柔轮材料力学性能影响的有限元分析

祝晋旋1，王家序1, 2，周青华1，周博1，龙见炳3

(1. 四川大学 空天科学与工程学院，四川 成都，610065； 2. 重庆大学 机械传动国家重点实验室，重庆，400040； 3. 贵州群建精密机械有限公司 技术部，贵州 遵义，563003)

以柔轮常用15-5ph不锈钢为对象，研究不同表面处理工艺对柔轮材料力学性能的影响规律。利用纳米压痕仪开展15-5ph不锈钢试件压入实验，将得到的载荷−深度曲线与有限元模拟结果进行对比，验证有限元压入模型的有效性。在此基础上，开展常见表面处理工艺影响柔轮材料力学性能的有限元建模与分析。研究结果表明：涂层弹性模量的增加将提高涂层−基体系统的等效硬度及刚度；渗碳层厚度的适当增大可减小柔轮基体应力而不影响柔轮的啮合精度；由喷丸产生的残余压应力越大，基体材料等效硬度越大，并可带来材料等效刚度的一定提高。

谐波减速器；表面处理；柔轮；有限元分析

谐波减速器与常规齿轮传动相比，具有传动比大、体积小、质量轻和传动精度高等优点[1]，广泛运用于航空航天、工业机器人等领域。柔轮是谐波减速器关键零部件之一，其齿面磨损是谐波减速器传动性能退化的主要原因[2]。工程中通常通过一些表面处理工艺如涂层、渗碳/氮、喷丸等提高柔轮齿面的耐磨损能力。同时，柔轮材料经过表面处理后，其力学性能或等效力学性能也将发生改变，会对谐波减速器的运行性能产生影响。例如，软涂层的施加可使齿面材料等效硬度减小，增大柔轮与刚轮齿面啮合时的接触面积，进而减少接触压力及齿面磨损；渗碳/氮可使齿面材料硬度增大，减小减速器的运行回差，提高运行精度。因此，开展表面处理工艺对柔轮材料力学性能影响研究对于更好地掌握谐波减速器服役行为具有重要意义。表面处理工艺只改变柔轮表层材料性能。然而对表层材料，使用传统的力学实验法难以有效获得其力学性能，必须依赖新型材料力学实验方法。微/纳米压痕法是近几十年来逐渐发展起来的一种新型材料测试技术，具有载荷小、分辨率高的特点，不仅可以在微/纳米尺度范围内精确测量材料的硬度、弹性模量等力学性能，还可以提供材料表面的力学性能和变形行为等信息，是测试经历表面处理材料力学性能的理想方法[3−4]。许多研究者提出了各种利用压痕实验获得材料性能的方法[5−14]，其中以OLIVER等[5]于1992年提出的通过压痕技术测量弹性模量和硬度的方法最具代表性，已被广泛应用于微观尺度下材料性能的测试。有限元方法作为可有效分析各种工程问题的重要工具，近年来在微/纳米压入模拟方面已得到广泛应用。有限元方法能与压痕实验结合，对压入过程进行数值模拟，并能方便地研究特定参数对压入过程的影响，从而大幅减小实验工作量和成本[15]。王晓宇等[16]利用有限元方法对不同薄膜参数下的薄膜/基体系统的力学性能进行了模拟研究；张帆等[17]采用有限元方法研究了摩擦因素对微压痕实验的影响；马永等[18]结合有限元方法讨论了不锈钢基体对Ti及Cr薄膜的影响规律；WARREN等[15]结合纳米压痕实验和有限元方法，对机加工表面引起的材料参数变化及影响规律进行了研究；JEONG等[19]利用有限元技术研究了压头变形量对材料硬度测量的影响；WALTER等[20]利用有限元方法研究了表面粗糙度对薄膜压痕的影响。本文作者以在谐波柔轮中广泛使用的15-5ph不锈钢材料为研究对象，使用有限元方法模拟压入过程，并与实验结果对比证实有限元压入模型的正确性。在此基础上开展不同表面处理工艺对柔轮材料力学性能影响规律的研究，研究结果将为柔轮材料表面工艺的优化设计提供理论指导。

1 压痕实验与有限元建模

1.1 压痕实验

以谐波减速器柔轮材料为研究对象，选取15-5ph长方体块作为实验试件，开展柔轮材料力学性能的 研究。

压痕实验采用Anton Paar公司的TTX−NHT2纳米压痕仪。该压痕仪最大压入载荷为0.5 N。待测试试件为长×宽×厚为30 mm×30 mm×11 mm的长方体块。表面经过抛光处理，粗糙度a小于0.2 µm。实验采用三棱锥形Berkovich压头。

1.2 有限元建模

根据LI等[21]的研究，使用半角为70.3°的圆锥形压头和Berkovich压头分别进行相同压入深度的压痕实验，二者得到的载荷−深度曲线一致，即可认为半角为70.3°的圆锥形压头在纳米压痕实验中与Berkovich压头是等效的。因圆锥形压头的结构和载荷在压痕实验中具有对称性，有限元模拟时可将三维模型简化为二维轴对称模型，大幅减少模型求解时间，并易于加密接触区域网格以提高求解精度。基于上述优点，采用二维轴对称模型对压入过程进行模拟。

所建立有限元模型的网格分布如图1所示。为保证求解精度，在接触区域采用细化网格，单元类型为CAX3；非接触区域适当增大网格尺寸，单元类型为CAX4。模型共18 496个节点，28 225个单元。因纳米压痕实验中使用压头为金刚石压头，其硬度和刚度远比试件材料的大，在压入过程中变形量非常小，故在有限元模型中将其简化为刚体。模型的边界条件按轴对称边界条件设置，被压材料沿对称轴方向上所有节点水平位移为0，下表面上所有节点的轴向位移为0，压头只允许沿竖直方向移动。在有限元模型中，使用力加载和位移加载可以得到一样的结果，两者相互等效。由于在有限元模型中位移加载方式较力加载方式更易计算收敛，故本文采用位移加载方式模拟实验采用的力加载方式，以减小模型收敛的难度。根据实验结果，有限元模型位移加载为压头沿轴负方向移动1.199 3 µm。

图1 有限元压入模型及网格划分

实验用15-5ph不锈钢弹性模量为200 GPa，屈服强度为1 907.3 MPa，泊松比为0.3。将有限元模拟结果与实验得到的载荷−深度曲线进行对比，如图2所示。从图2可以看出：有限元模拟结果与实验结果具有较好的一致性，由此证实了有限元模拟压入过程的有效性和本文所建立有限元模型的正确性。

图2 有限元与实验得到的载荷−深度曲线对比

2 结果与讨论

以表面涂层、渗碳/氮以及喷丸等几种常见的表面处理工艺为例，基于有限元方法分析表面处理工艺参数对柔轮材料力学性能的影响。

2.1 涂层对柔轮材料力学性能的影响分析

涂层是表面处理方法中极为重要的技术之一，它是运用表面冶金强化或表面镀膜强化对材料表面进行防护或修复的技术[22]。涂层材料、厚度及涂层层数的选取是涂层工艺设计中极为重要的一环。针对表面涂层工艺下的有限元压入模拟均基于以下假设：

1) 涂层与基体理想固结；

2) 涂层材料各向同性；

3) 涂层在基材上制备均匀，不会产生局部应力过大现象。

2.1.1 涂层弹性模量的影响

设定涂层厚度为1.25 µm，涂层的弹性模量分别为50，100，200和400 GPa。图3所示为涂层具备不同弹性模量时涂层−基体系统的载荷−深度曲线。由图3可知：在相同压入深度时，随着涂层弹性模量的增大，压头受到的反作用力变大，即随着涂层弹性模量的增大，涂层−基体系统的等效硬度也随之变大。另一方面，压痕曲线卸载部分的斜率也随着涂层弹性模量的增大而增大。根据压痕理论，材料的接触刚度为压痕曲线卸载部分的斜率。因此，压痕卸载曲线表明随着涂层弹性模量的增大，涂层−基体系统的刚度将随之增大，有利于柔轮啮合精度的保持。

图3 涂层弹性模量对载荷−深度曲线的影响

图4所示为最大压深时，不同弹性模量涂层−基体系统内部von Mises应力分布情况。从图4可以看出：当涂层弹性模量为100 GPa及200 GPa时，涂层−基体系统的最大应力均为2 050 MPa，但两者的应力分布则不同。涂层弹性模量为100 GPa时，涂层−基体系统的最大应力位于基体中，涂层上的应力相对较小。这是因为软涂层的屈服强度比基体的小，涂层在达到自身的屈服极限后应力不再线性增加。而当涂层弹性模量为200 GPa时，即涂层材料为基体本身时，两者的屈服性能一样，因而涂层−基体系统的应力分布是连续的。对于涂层弹性模量为400 GPa的情况，涂层−基体系统的最大应力为3 815 MPa。与软涂层类似，因涂层屈服强度比基体的大，因而最大应力位于涂层上而不是基体中。综上，外载作用下，在变形量足够大时，涂层−基体系统的应力及分布取决于涂层与基体之间的材料属性差异。

图4 涂层弹性模量不同时涂层−基体系统内部应力分布

不同外载作用下，涂层−基体系统的应力场反应往往更能说明涂层对基体材料力学性能的影响。图5所示为不同加载深度时基体最大von Mises应力的变化曲线。从图5可以看出：涂层弹性模量越大，相同压入深度时，基体应力越大，同时基体的应力越容易达到最大值。谐波减速器在实际使用中，选取弹性模量较小的软涂层，可以有效减小基体的应力，从而有效保护柔轮基体。因此，仅从保护基体的角度来看，软涂层对基体的保护作用大于硬涂层。

图5 不同涂层弹性模量下基体最大von Mises应力随压入深度变化曲线

2.1.2 涂层厚度的影响

设定涂层材料的弹性模量为100 GPa，在此基础上改变涂层厚度，研究不同涂层厚度对柔轮基体材料力学性能的影响规律。涂层厚度分别设定为0.50，1.25，2.00，2.75，3.50和4.25 µm。

图6所示为不同涂层厚度时涂层−基体系统的载荷−深度曲线。由图6可知：在相同压入深度时，涂层厚度越大，压头受到的反作用力越小，说明软涂层厚度越大，涂层−基体系统的等效硬度越小。这是因为软涂层自身硬度比基体的小，随着涂层厚度的增加，涂层−基体系统将越来越多地表现出涂层的力学性能。从图6还可以看出：压痕曲线卸载部分的斜率随着涂层厚度的增加而逐渐减小，说明涂层−基体系统的等效弹性模量随着涂层厚度的增加而减小，这可能使谐波减速器的刚轮和柔轮在啮合时变形增大，不利于啮合精度的保持。

图6 不同涂层厚度对载荷−深度曲线的影响

图7所示为不同涂层厚度下基体最大von Mises应力随压入深度变化的曲线。从图7可以看出：随着涂层厚度的增大，基体的应力达到最大值所需要的压入深度越大。因此，与前节结论一致，增大软涂层厚度可以有效地保护基体。但需要注意的是，工程中不能一味地增大涂层厚度，一方面是由于涂层成本比较高，另一方面软涂层厚度增加对减速器啮合精度的保持会产生不利影响。因此，对涂层厚度的选取应根据减速器的使用工况从多方面进行综合考虑。

图7 不同涂层厚度下基体最大von Mises应力随压入深度变化曲线

2.1.3 涂层层数的影响

除单层涂层外，工程中也常采用多层涂层对材料表面进行处理，以得到合适的强化表面。设定涂层总厚度1.25 µm不变，研究涂层层数对涂层−基体系统力学性能的影响规律。多层涂层的材料参数设置如表1所示，涂层沿深度方向逐渐接近基体弹性模量。

图8所示为涂层层数不同时的涂层−基体系统的载荷−深度曲线。从图8可以看出：单涂层与多涂层表现差异明显，并且随着涂层层数的增加，压头上的反作用力越大。然而，对于多涂层情形时，载荷−深度曲线虽然非常相似，但仍存在随着涂层层数的增加，作用在压头上的反作用力也随之变大的规律。总体而言，相对于单层涂层而言，多涂层方案可以有效增加涂层−基体系统的等效硬度。而对于多层涂层，涂层−基体系统的等效硬度变化并不大。因此，工程实践中如无特殊需求，选取两层涂层较为合适。

表1 多层涂层材料的弹性模量

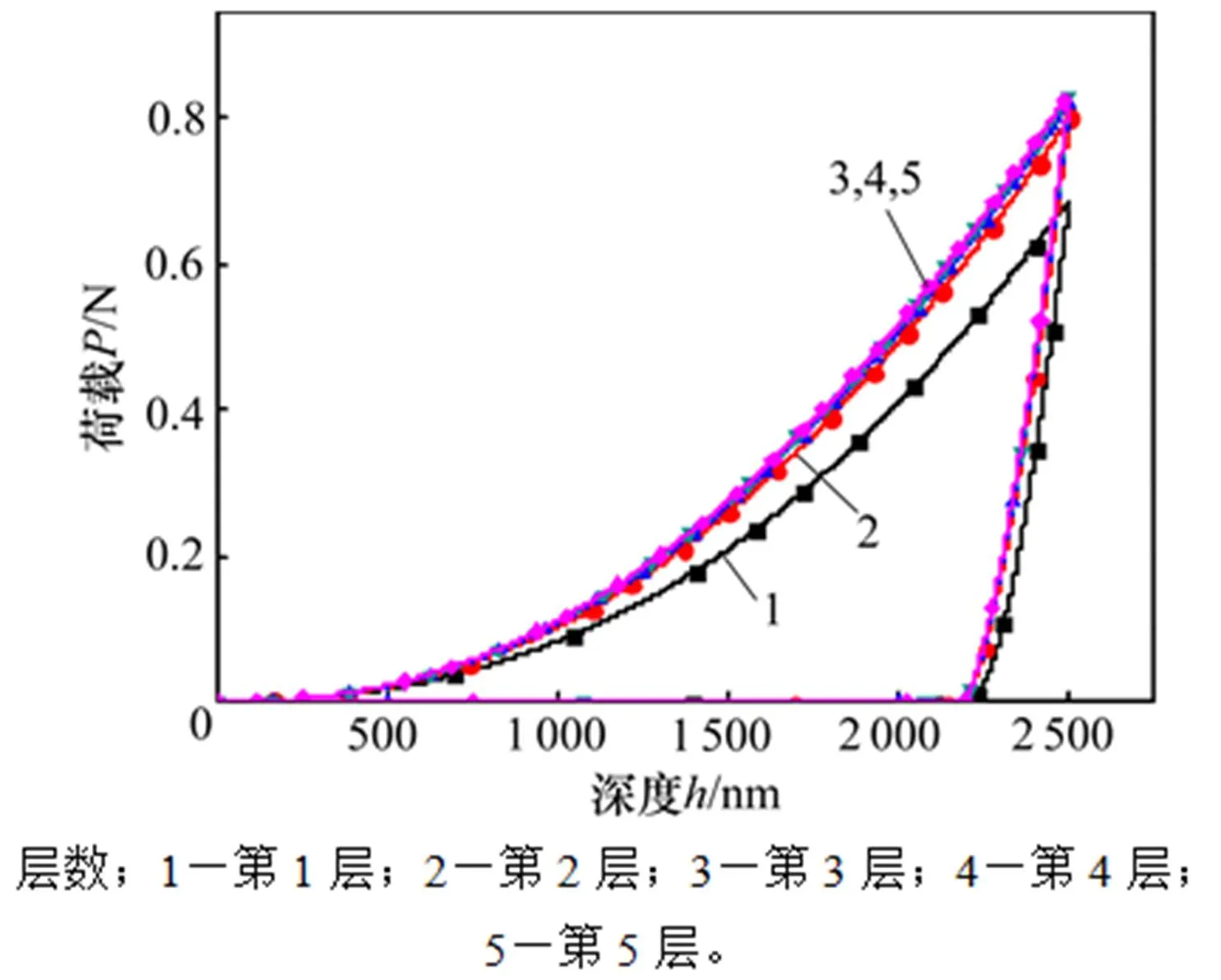
图8 不同涂层层数对载荷−深度曲线的影响

2.2 渗碳对柔轮材料力学性能影响分析

渗碳热处理广泛应用于承受着高负荷、高磨损和高疲劳抗力的零件生产[23]，是一种重要的齿轮表面处理技术。柔轮在特定应用中由于耐磨性需求，也会采用浅层渗碳工艺。渗碳热处理工艺中，采用合适的工艺方法可以控制渗碳表面的碳浓度，从而控制渗碳层的硬度。假设渗碳层的碳浓度可以得到完美控制，并可以形成弹性模量及屈服强度呈连续梯度变化的渗碳层。

2.2.1 渗碳层厚度的影响

以渗碳层的表层为起始层，弹性模量为400 GPa，经渗碳层与基体的交界层为终止层，弹性模量为200 GPa，弹性模量由起始层到终止层均匀连续变化。渗碳层厚度分别设定为0.50，1.25，2.00，2.75，3.50和4.25 µm。

图9所示为渗碳层厚度不同时的渗碳层−基体系统的载荷−深度曲线。从图9可以看出：改变渗碳层厚度，涂层−基体系统的载荷−深度曲线的变化并不大，说明改变梯度材料厚度并不能明显改变渗碳层−基体系统的力学性能。

图9 不同渗碳厚度对载荷−深度曲线的影响

不同渗碳层厚度下基体最大von Mises应力−压入深度变化曲线如图10所示。从图10可以看出：随着渗碳层厚度的增大，基体的应力达到最大值所需要的压入深度越大，这与涂层厚度的规律类似。不同的是，渗碳层的硬度一般要大于基体，渗碳层厚度可以适当增大，可以对柔轮基体形成保护，而不必担心影响柔轮的啮合精度。

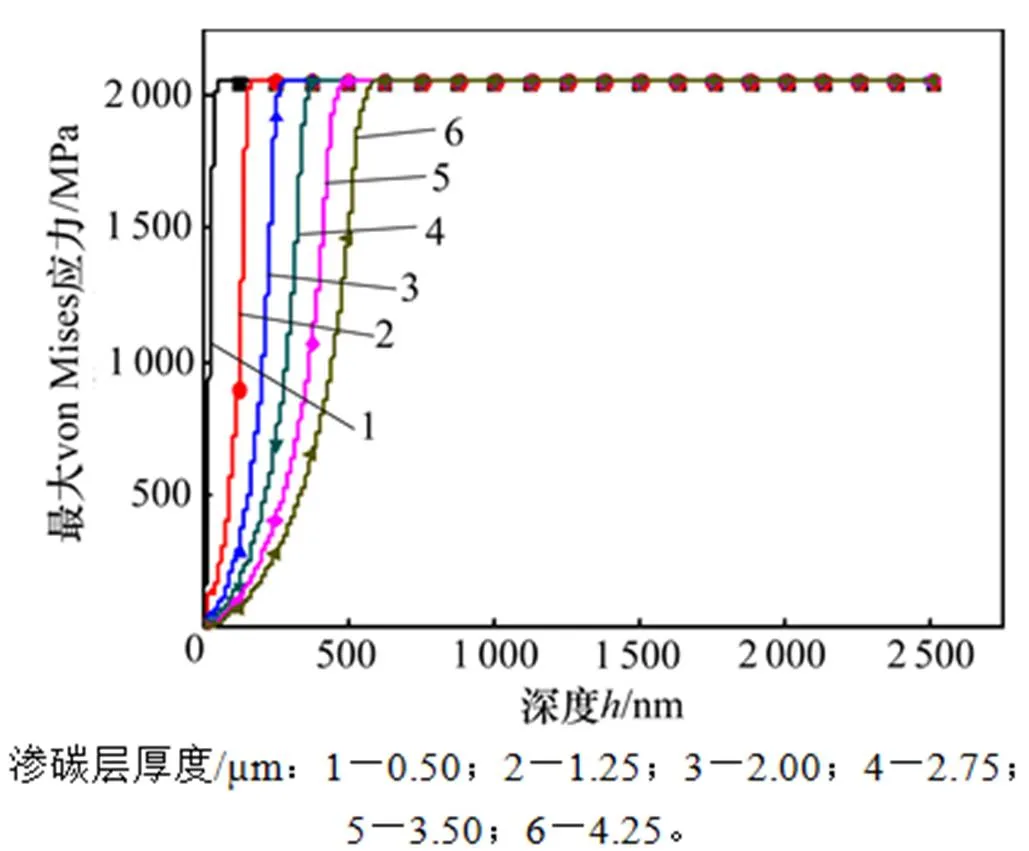
图10 不同渗碳厚度下基体最大von Mises应力随压入深度变化曲线

2.2.2 渗碳层弹性模量的影响

在渗碳层厚度相同的情况下，控制碳浓度在渗碳层中的分布，可得到由表层到底层弹性模量呈不同梯度变化的渗碳层。设定渗碳层厚度为1.25 µm，渗碳层表层弹性模量分别为250，300，350和400 GPa，底层弹性模量则均为200 GPa。不同材料梯度对载荷−深度曲线的影响如图11所示。由图11可知：改变渗碳层材料梯度变化规律，渗碳层−基体系统的载荷−深度曲线的变化甚为微小，因此，以改变渗碳梯度方式来改变渗碳层−基体系统在力学方面的性能的作用有限。

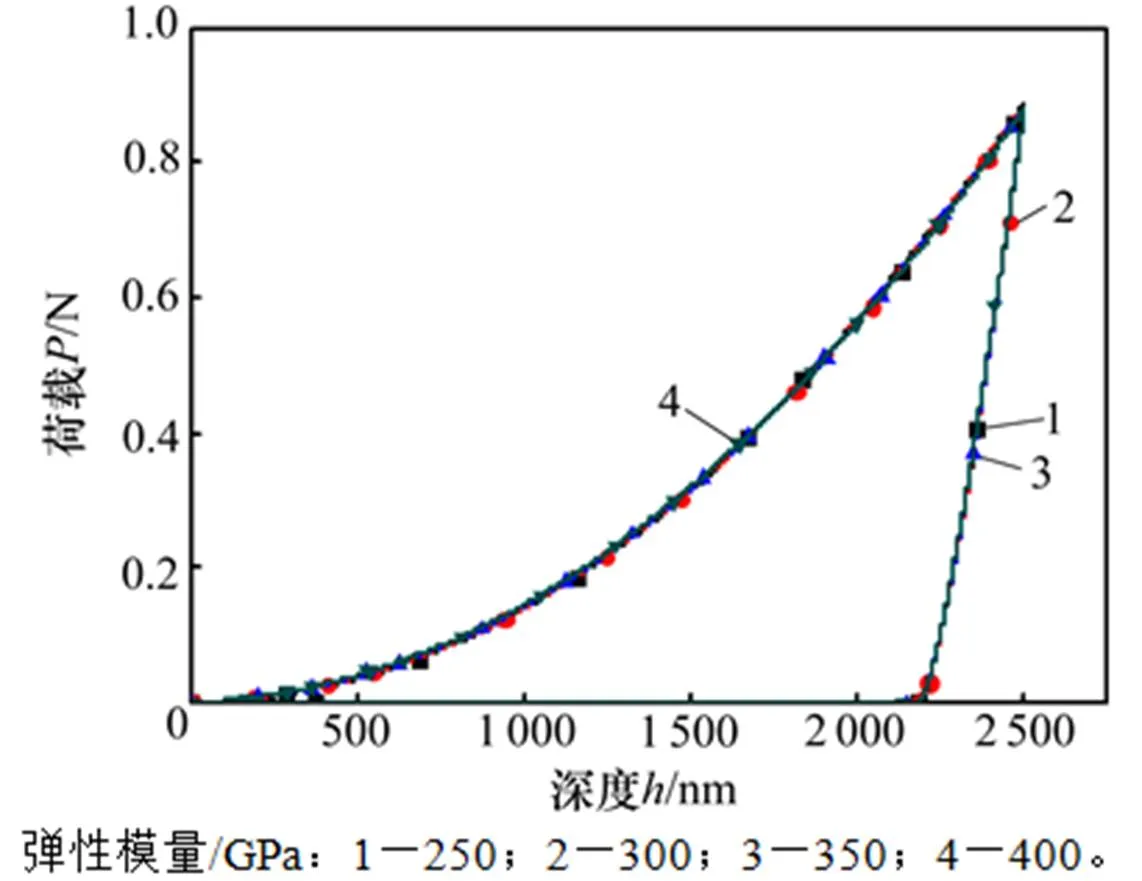
图11 不同材料梯度对载荷−深度曲线的影响

2.3 喷丸的影响

喷丸即通过丸粒轰击工件表面并植入残余应力，以达到提高零件机械强度以及耐磨性的目的[24]。与涂层、渗碳类似，经过喷丸处理后，零部件表面的材料力学性能同样会发生改变。其中最重要的改变就是喷丸将引起表层材料中较大的残余压应力。此外，针对柔轮材料的热/表面处理工艺中均会产生残余应力 分布。

因喷丸对试样组织的影响一般在表层几十微米的深度范围内，故采用在距离压入表面20 µm的基体材料区域中施加相等的残余压应力来模拟喷丸造成的残余压应力。将残余压应力分别设定为200，400，600和800 MPa，并与不存在残余应力的情况进行对比，得到了载荷−深度曲线(如图12所示)。从图12可以看出：压入相同深度时，随着材料内部残余压应力的增大，压头的受到的反作用力随之增大，即残余压应力能增加材料的等效硬度，且残余压应力越大，等效硬度越大。分析结果同时也反映出如果试件中存在残余应力，将明显影响压痕实验对材料力学性能的测量精度。因此，对某种未知材料进行力学性能测定时，要保证待测试样不存在残余应力，否则将影响对试样力学性能测定结果的准确性。

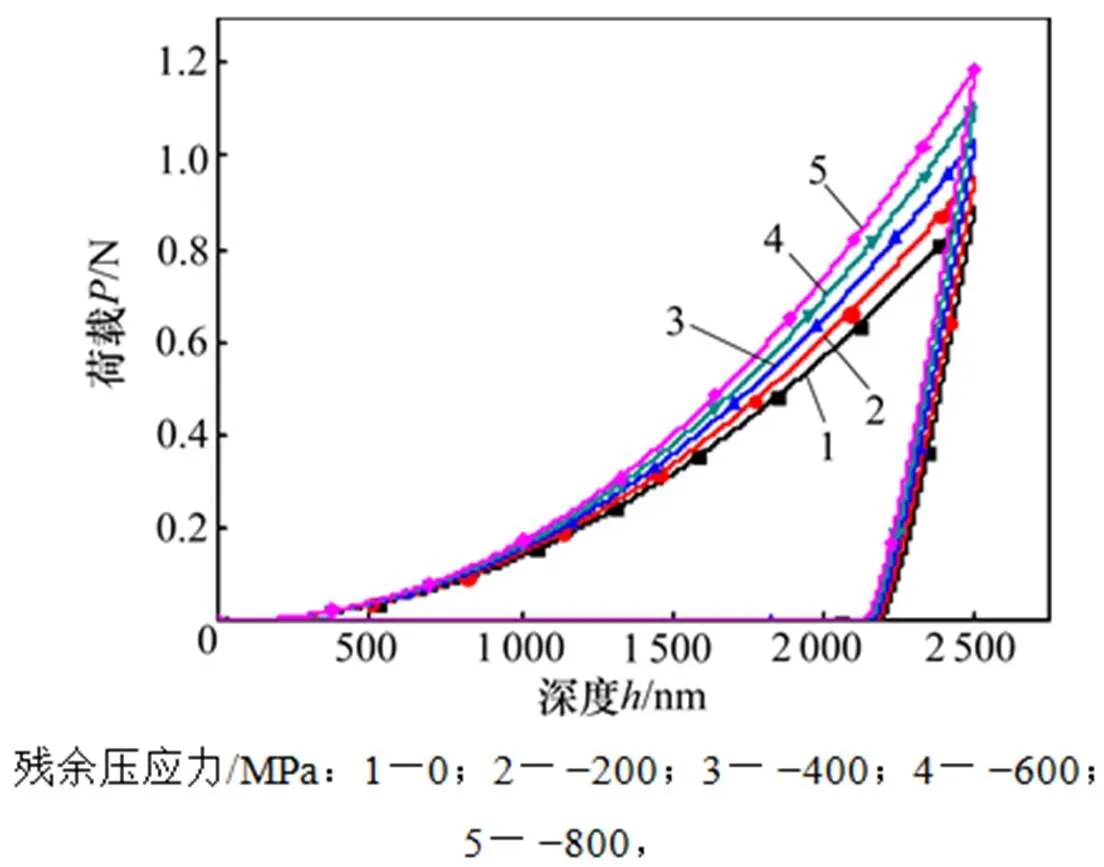
图12 不同预设残余压应力对载荷−深度曲线的影响

表2所示为基体存在残余应力时残余深度与最大压深的比值。从表2可以看出：随着残余压应力的增大，基体的残余深度呈现出逐渐减小的趋势，说明残余压应力在一定程度上可以提高材料的等效刚度。

表2 不同预设残余应力下残余深度与最大压入深度的比值

3 结论

1) 对15-5ph不锈钢试件进行压入实验，并将实验结果与有限元模拟结果进行对比，验证了有限元模拟压入过程的有效性及文中所建有限元模型的正确性。

2) 随着涂层弹性模量的增大，涂层−基体系统的等效硬度及刚度也随之增大；涂层−基体系统的等效弹性模量随着软涂层厚度的增加而减小；相对双层涂层，多层涂层对涂层−基体系统的等效力学性能改变有限。

3) 改变梯度渗碳层厚度不能明显改变渗碳层−基体系统的力学性能，但渗碳层厚度的适当增大，可减小柔轮基体应力而不影响柔轮的啮合精度；渗碳层厚度相同时，改变渗碳梯度对渗碳层−基体系统力学性能影响不大。

4) 喷丸造成的残余压应力能增加材料的等效硬度，残余压应力越大，等效硬度越大；且喷丸在一定程度上可以提高材料的等效刚度。

[1] FUSARO R L. Preventing spacecraft failures due to tribological problems[R]. Cleveland: Glenn Research Center, NASA, 2001: 1−20.

[2] 夏田, 江鹏, 马超, 等. 谐波减速器柔轮摩擦磨损及失效机理研究进展[J]. 机械传动, 2016, 40(1): 173−176. XIA Tian, JIANG Peng, MA Chao, et al. Research advance of the failure mechanism and friction wear of flexible wheel of harmonic reducer[J]. Journal of Mechanical Transmission, 2016, 40(1): 173−176.

[3] FANG T H, JIAN SH R, CHU D S. Nanomechanical properties of TiC, TiN and TiCN thin films using scanning probe microscopy and nanoindentation[J]. Applied Surface Science, 2004, 228(1): 365−372.

[4] CHEN S H, LIU L, WANG T. Investigation of the mechanical properties of thin films by nanoindentation, considering the effects of thickness and different coating-substrate combinations[J]. Surface & Coatings Technology, 2005, 191(1): 25−32.

[5] OLIVER W C, PHARR G M. An improved technique for determine hardness and elastic modulus using load and displacement sensing indentation experiments[J]. Journal of Materials Research, 1992, 7(6): 1564−1583.

[6] CHENG Y T, CHENG C M. Relationships between hardness, elastic modulus, and the work of indentation[J]. Applied Physics Letters, 1998, 73(5): 614−616.

[7] DAO M, CHOLLACOOP N, Van VLIET K J, et al. Computational modeling of the forward and reverse problems in instrumented sharp indentation[J]. Acta Materialia, 2001, 49: 3899−3918.

[8] MA D J, ONG C H W, WONG S F. New relationship between Young’s modulus and nonideally sharp indentation parameters[J]. Journal of Materials Research, 2004, 19(7): 2144−2151.

[9] MENČÍK J. Determination of mechanical properties by instrumented indentation[J]. Meccanica, 2007, 42(1): 19−29.

[10] SABER-SAMANDARI S, GROSS K A. Effect of angled indentation on mechanical properties[J]. Journal of the European Ceramic Society, 2009, 29(12): 2461−2467.

[11] KIM H H, CHO S H, KANG C G. Evaluation of microstructure and mechanical properties by using nano/micro-indentation and nanoscratch during aging treatment of rheo-forged Al 6061 alloy[J]. Materials Science & Engineering A, 2008, 485(1/2): 272−281.

[12] SUN G, XU F, LI G, et al. Determination of mechanical properties of the weld line by combining micro-indentation with inverse modeling[J]. Computational Materials Science, 2014, 85(4): 347–362.

[13] SHEDBALE A S, SINGH I V, MISHRA B K, et al. Evaluation of mechanical properties using spherical ball indentation and coupled finite element–element-free galerkin approach[J]. Mechanics of Advanced Materials & Structures, 2016, 23(7): 832−843.

[14] LI Y, STEVENS P, SUN M, et al. Improvement of predicting mechanical properties from spherical indentation test[J]. International Journal of Mechanical Sciences, 2016, 117: 182−196.

[15] WARREN A W, GUO Y B. Machined surface properties determined by nanoindentation: Experimental and FEA studies on the effects of surface integrity and tip geometry[J]. Surface & Coatings Technology, 2006, 201: 423−433.

[16] 王晓宇, 王金良, 彭洪勇. 有限元分析薄膜/基底在纳米压痕过程中的力学性能[J]. 人工晶体学报, 2014, 43(2): 327−332. WANG Xiaoyu, WANG Jinliang, PENG Hongyong. Finite element analysis on the mechanical properties of the film/substrate system in the process of nanoindentation[J]. Journal of Synthetic Crystals, 2014, 43(2): 327−332.

[17] 张帆, 黄克智, 黄永刚, 等. 摩擦因素对微压痕实验的影响[J]. 工程力学, 2006, 23(S1): 1−6. ZHANG Fan, HWANG Kehchih, HUANG Yonggang, et al. Friction effect on indentation[J]. Engineering Mechanics, 2006, 23(S1): 1−6.

[18] 马永, 于海峰, 田林海, 等. 有限元法分析不锈钢基体对Ti及Cr薄膜的影响[J]. 稀有金属材料与工程, 2014, 41(S2): 553−556. MA Yong, YU Haifeng, TIAN Linhai, et al. Effect of AISI-304 SS substrate on Ti and Cr thin films with finite element simulation[J]. Rate Metal Materails and Engineering, 2014, 41(S2): 553−556.

[19] JEONG S M, LEE H L. Finite element analysis of the tip deformation effect on nanoindentation hardness[J]. Thin Solid Films, 2005, 492(1): 173−179.

[20] WALTER C, ANTRETTER T, DANIEL R, et al. Finite element simulation of the of surface roughness on nanoindentation of thin films with spherical indenters[J]. Surface & Coating Technology, 2007, 202(4): 1103−1107.

[21] LI Min, CHEN Weimin, LIANG Naigang, et al. A numerical study of indentation using indenters of different geometry[J]. Journal of Materials Research, 2004, 19(1): 73−78.

[22] 胡传炘. 涂层技术原理及应用[M]. 北京: 化学工业出版社, 2000: 1−10. HU Chuanxin. Principle and application of coating technology[M]. Beijing: Chemical Industry Press, 2000: 1−10.

[23] 朱祖昌, 许雯, 王洪. 国内外渗碳和渗氮工艺的新进展(一)[J]. 热处理技术与装备, 2013, 34(4): 1−8.ZHU Zuchang, XU Wen, WANG Hong. Novel development of carburizing and nitriding technology at home and abroad (1)[J]. Heat Treatment Technology and Equipment, 2013, 34(4): 1−8.

[24] 孙希泰. 材料表面强化技术[M]. 北京: 化学工业出版社, 2005: 296−297.SUN Xitai. Surface hardening technology[M]. Beijing: Chemical Industry Press, 2005: 296−297.

(编辑 赵俊)

Finite element analysis on influence of surface treatments on mechanics of flexible gear material

ZHU Jinxuan1, WANG Jiaxu1, 2, ZHOU Qinghua1, ZHOU Bo1, LONG Jianbing3

(1. School of Aeronautics & Astronautics, Sichuan University, Chengdu 610065, China; 2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China; 3. Technology Department, Guizhou Qunjian Precision Machinery Co. Ltd, Zunyi 563003, China.)

The influence of different surface treatment processes on the mechanics of 15-5ph stainless steel, which is commonly used for flexible gear, was studied. Firstly, a 15-5ph stainless steel specimen was tested by a nano-indentation tester. The obtained load−displacement curve was compared with that simulated by finite element method, verifying the effectiveness of the indentation model established by the finite element method. Based on the above results, the influence of different surface treatments on the flexible gear material was modeled and analyzed. The results show that increasing coating’s elastic modulus can increase the equivalent hardness and stiffness of coating-matrix system; and that increasing carburizing layer thickness appropriately reduces the stress of flexible gear matrix without affecting engage precision. If the residual compressive stress caused by shot peening becomes larger, the equivalent hardness of the matrix material gets larger, and in the meanwhile, the equivalent stiffness will be improved to some extent.

harmonic drive; surface treatment; flexible gear; finite element analysis

TH132.43

A

10.11817/j.issn.1672-7207.2018.03.011

1672−7207(2018)03−0592−08

2017−03−05；

2017−05−30

国家自然科学基金资助项目(51405316，51435001)；国家高技术研究发展计划(863计划)项目(2015AA043001)；航空科学基金资助项目(20150219001) (Projects(51405316, 51435001) supported by the National Natural Science Foundation of China; Project(2015AA043001) supported by the National High Technology Research and Development Program (863 Program) of China; Project(20150219001) supported by the Aeronautical Science Foundation of China)

周青华，副研究员，从事空间摩擦学与可靠性工程、多尺度优化设计理论研究；E-mail: qh.zhou@foxmail.com