基于概念密度泛函理论磷酸酯类反应性物质毒性预测
2018-04-10丁晓琴丁俊杰李大禹潘里裴承新
丁晓琴,丁俊杰,李大禹,潘里,裴承新
1 引言
大多数有机磷酸酯类化合物都是乙酰胆碱酯酶不可逆抑制剂。不可逆抑制剂不同于一般的配体与受体相互作用,它涉及到旧化学键的断裂和新化学键的形成,即发生化学反应的过程。因此在构建与受体相互作用的化学反应性物质的定量构效关系(QSAR)或定量构性关系(QSPR)方程时,会遇到一些独特的困难与问题1,2。目前,QSAR使用的描述参数大多数是非反应性的,例如传统的立体参数、电性参数、疏水参数,以及后来不断发展的各种分子结构性质描述参数等3-7,这些参数中的多数没有涉及到化合物在发生化学反应过程中的电子转移变化,从而不能有效和精确地描述化合物在体内与酶或受体等发生化学反应的作用机制,进而导致构建的反应性物质的 QSAR或QSPR模型预测性能较差。
随着量子化学理论、计算方法以及计算机技术的迅速发展,特别是近十几年来概念密度泛函理论(Conceptual Density Functional Theory,CDFT)的发展,使得化学反应性物质的毒性虚拟评估成为可能。概念密度泛函理论是密度泛函理论(DFT)的一个重要分支,又称为密度泛函活性理论或化学密度泛函理论8-11。它是从 DFT理论中把与化学相关的概念和原理提取出来,通过理论推导,获得参数的计算方法12-14。这些参数主要包括电负性、硬度、软度、福井函数、亲电性等一系列新型的量子化学描述符指数。一方面通过分子的化学势来描述分子在体系中的反应性能;另一方面通过分子中各个原子的电荷密度来描述体系中可能发生化学反应的重点部位15-19。概念密度泛函理论方法得到的一系列新型电子结构描述参数,是一类新的专门用于描述化学反应性物质的结构指数。本文应用概念密度泛函理论,对磷酸脂类乙酰胆碱酯酶不可逆抑制剂的反应性指数进行系统的理论计算,探索该类描述指数在构建精确 QSPR模型方面的应用,进而实现对磷酸酯类反应性物质毒性的高精度预测。这方面的研究内容在国内外还未见相关的报道。
2 理论与计算方法
2.1 理论
在概念密度泛函理论中,通过两种微扰对分子体系基态能量Ε的影响,来研究各种物理化学性质的变化。根据Hohenberg-Kohn定理,两种微扰一个是体系总电子数Ν的变化,另一个是外势ν的变化,分别以dΝ微扰和dν微扰表示。对于分子体系,外势 ν通常指原子核形成的库伦势,外势的变化可以是几何构型或构象的改变,也可以是与其它分子相互作用时相对位置的变化。在微扰的影响下,体系性质的改变可以用敏感度系数(sensitivity coefficient)来表示。我们感兴趣的敏感度系数是体系基态对微扰dΝ和微扰dr的一阶、二阶响应函数的变化,甚至三阶和更高价的响应函数(其真正的物理和化学意义正在探索研究和发展过程中)。通过对分子体系的能量泛函Ε[ρ(r)]=Ε[Ν, r]求微商,可以得到各种敏感度系数,包括化学势、电负性、硬度、软度、福井函数等等。下面对本文研究密切相关的几个反应性参数进行简要说明:
一阶响应函数:可以获得化学势 μ和电子密度ρ等。
化学势:

电子密度:

根据有限差分原理,化学势近似从计算分子垂直电离势I和亲和势A中获得。化学势μ的负值是电负性χ。
二阶响应函数:可以获得体系硬度、软度、福井函数等。
整体硬度:

体系整体硬度(global hardness, η)表示的是当外势不变,化学势随着电子数目的改变而变化的速率。
整体软度:

体系整体软度(global softness, S)与体系整体硬度之间存在倒数关系。
亲电指数:

局域硬度20:

局域硬度又称硬度密度(hardness density),描述在外势不变的条件下,体系化学势随 r处电子密度改变而改变的难易程度。
局域软度:

局域软度用以衡量在外势不变的情况下,体系某点的电子密度对体系化学势微扰的敏感程度。整体软度与局域软度的关系S是:S = ∫s(r)dr,而局域软度则是:
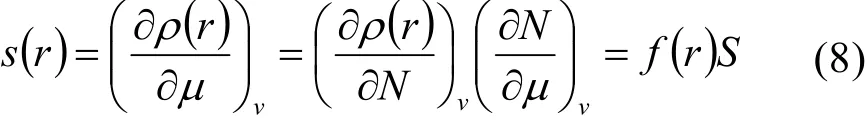
上式局域软度包含了福井函数和整体软度的信息,即包含了相对反应物而言的整体反应性-硬度或软度。
福井函数:

福井函数用来描述分子内的反应顺序,即同一个分子结构中不同位置的相对反应活性信息,而局域软度可用来研究分子间的反应顺序。这两个都是量子化学反应性最重要的定量描述参数。同时,局域软度还可度量体系化学势对某区域外势微扰的敏感程度,因此有可能包含分子中不同位置相对反应性的信息。
福井函数是一个局域性质,即分子中不同的位置有不同的值。因此,福井函数为研究化学反应的区域选择性或确定生物体系的活性中心提供了有力的工具。表示在外势不变的条件下,分子体系的总电子数发生改变时,分子中区域j点的电子数变化率;或者分子体系的总电荷发生改变时,区域j点的电荷变化率。应用有限差分近似,福井函数f(r)可表示为,
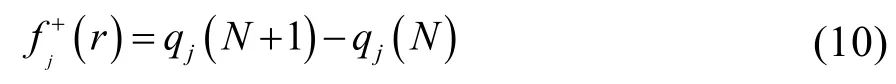
亲核福井函数:表示当分子得到1个电子时,第j原子的电荷变化率。

亲电福井函数:表示当分子失去1个电子时,第j原子的电荷变化率。
自由基攻击福井函数:

表示当分子的某一原子受到自由基攻击时的电荷变化率。
上式中 qj(Ν),qj(Ν + 1),qj(Ν - 1)分别表示分子为中性、阴离子和阳离子时,分子中原子j所带的电荷;fj+(r)和 fj-(r)分别为亲核进攻指数和亲电进攻指数,表示分子中的原子j给电子和得电子能力的强弱,而 fj0(r)为自由基攻击指数,其值大小反映自由基进攻的能力。
前线分子轨道是控制化学反应的难易程度、反应区域及立体选择性的重要因素:最高占有轨道(HOMO)控制着亲电反应位置,而最低空轨道(LUMO)是控制着亲核反应位置。
2.2 计算方法
本文通过对磷酸酯类化合物的结构性质分析,选择了 15个具有大鼠腹腔半数致死剂量(LD50)活性的各种结构类型化合物作为训练集21,包括有机磷酸酯类杀虫剂和部分神经性毒剂,毒性范围跨越 5个数量级以上。首先分别在气相和水溶液相(CPCM模型)条件下,采用B3LYP/6-311++G(2d,3p)基组对分子进行了结构优化。然后我们采用 MP2/6-311++G(2d,3p)及B3LYP/6-311++G(2d,3p)两个基组,分别在气相和水溶液条件下,进行分子结构描述参数计算。其中,NBO性质分别进行了中性分子(分子的电子数为Ν),得到一个电子(电子数为Ν + 1),失去一个电子(电子数为Ν - 1)条件下的计算。所有训练集和测试集分子的最低能量构象的结构与原子编号参见Supporting Information-图 S1。
计算得到分子的整体描述参数有:分子的垂直电离势I、垂直亲和势A、电子化学势μ、绝对硬度 η、亲电性指数 ω以及分子的前线轨道能量等。分子局域描述指数有:收敛的原子福井函数、原子NBO净电荷以及Wiberg键级等。上述计算获得的整体和局域的分子描述参数和疏水性参数等原始计算结果详见 Supporting Information-图S2。
采用上述计算的参数,应用逐步回归统计分析方法,构建四个条件(MP2和B3LYP、气相和溶液相)的线性方程,确定最合理的计算条件,化合物的毒性采用大鼠腹腔半数致死剂量的负对数(pLD50)。在此基础上,进一步采用遗传最小偏二乘方法(G/PLS),构建线性/非线性QSPR方程,主成分数分别设为 1-6,方程的长度设为 3-10,优化并选择合理的方程组用于测试集的毒性预测。
本文分子模型的构建采用GaussView 5.09软件,量子化学计算采用Gaussian09软件22,在曙光TC3600刀片服务器上完成。相关统计分析采用Cerius2软件23完成。另外应用ACD/Lab12.024学术下载版软件和HyperChem7.025评估程序计算了分子疏水性logP值、分子体积、表面积等参数。
3 结果与讨论
3.1 分子反应性分析
计算结果表明,四个计算条件得到的结果,整体趋势基本一致。为了便于说明,现将其中的一个条件,即:B3LYP/6-311++G(2d,3p)/gas的计算结果列于表 1-表 3(仅列出 15个训练集化合物的计算结果,包括了部分叔胺氮游离态和质子化态的结果)。
从上述结果可见:大多数分子的亲电反应中心都在磷原子上。但也有例外情况,如一些计算结果反映出化学反应有可能甚至优先发生在碳原子上,这可能与发生化学反应的类型有关;反应中心磷原子上的正电荷和磷的亲电进攻反应性并没有明显的相关性;分子中的最低键级,并不一定就是与酶反应中的离去基团,与得失电子后,分子键级的变化过程有关。例如含有 P―S键或P―N键的分子,在Ν - 1个电子的状态下,其键级的降低变化就比较大;任何单个反应性指数与毒性似乎没有明显的相关规律,这可能与其作用机制和动力学过程中的复杂性有关,多种因素的共同作用引起乙酰胆碱酯酶的活性抑制、毒性及老化。
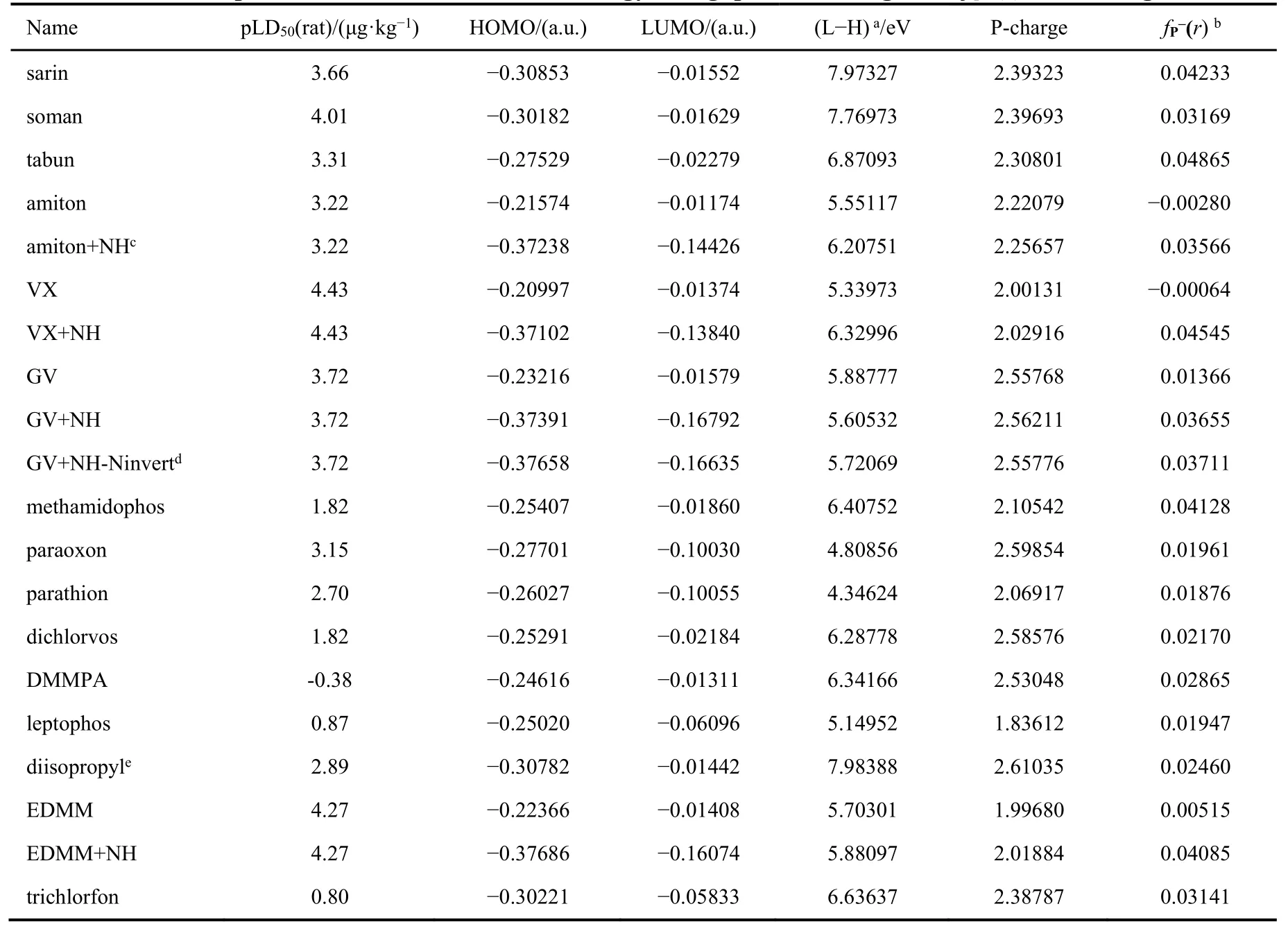
表1 训练集分子的pLD50毒性、前线轨道能量和能差、磷原子的NBO电荷和亲电反应指数fp-(r)Table 1 The pLD50 value, frontier orbital energy and gap, NBO charge and fp-(r) in training sets.

表2 训练集分子整体反应性指数Table 2 The global reactivity index for the training sets at B3LYP/6-311++G(2d,3p)/gas level.
3.2 氮原子不同质子化状态及构象对分子反应性影响
3.2.1质子化状态对分子反应性影响
Amiton、VX、GV和 EDMM 四个分子(化学结构见Supporting Information-S1),离去基团侧链上的乙胺基叔氮原子质子化成为胺基阳离子后,反应性指数计算结果的共同特点是:分子的HOMO和LUMO轨道能量显著降低,能量差增加;磷原子上的正电性增加;在气相和溶液相状态下,MP2方法计算氮原子的不同质子化状态都预测到磷中心的亲电反应性,而B3LYP方法在氮原子的非质子化状态,气相和溶液相都没有预测到磷中心的亲电反应性,氮原子质子化后,磷原子的亲电性发生了明显的转化,由非亲电反应中心转到较强的亲电反应中心;同时,分子的垂直电离势I增加、亲和势 A降低、I-A的能差显著增加,绝对硬度η增强、亲电性ω有所降低,说明质子化后,磷中心的亲电进攻反应性增强。
3.2.2构象对分子反应性影响
相同分子和质子化状态,不同构象的反应性指数计算结果表明,对大多数分子性质,例如前线轨道能量、原子电荷、键级、分子整体的反应性指数等,计算结果有微小的差别,相对于其它的误差,对回归结果不会产生本质的影响,采用分子的最低能量构象计算分子性质即可。但 MP2方法有时对构象的反应过分敏感,在同一个分子中,具有相同性质的碳,构象位置上稍有差异,对原子的亲电反应性就产生不可思议的差别,例如在二异丙基氟磷酸酯(Diisopropyl)分子中,两个P―O―C键上的碳原子亲电反应性应该基本类似,但计算结果显示,C6具有仅次于磷的第二个亲电反应中心的性质,另一个C8则基本没有亲电反应性,结果见表4。而B3LYP方法,在气相和溶液相都没有预测到C6和C8的亲电反应性的较大差异。
另一个方面,在大多数分子中磷中心的亲电反应性的计算值,MP2方法明显要高于B3LYP方法计算结果,在分子的键级变化方面也有类似的问题,说明MP2方法计算结果的不稳定性。

表3 关键原子间NBO键级及它们的得失1个电子后变化率Table 3 Pivotal NBO bond order and their variability after obtaining 1e or losing 1e.
3.3 反应性指数的QSPR研究
3.3.1QSPR方程构建
根据分子总体反应性指数分析,以及氮原子离子化状态、分子构象对反应性指数的影响,我们首先建立氮原子为质子化状态的 QSPR方程。应用逐步回归分析方法,分别构建训练集化合物在四组条件下计算的描述符与毒性pLD50的QSPR方程,得到方程 13至方程 16,其中 r2是回归方程的决定系数,Ftest值是显著性检验,XV_r2是交叉验证相关系数,BS_r2是 Bootstrap方法相关系数,Νobs表示构建方程时训练集的个数。
方程13 (B3LYP/gas):

方程14 (B3LYP/water):
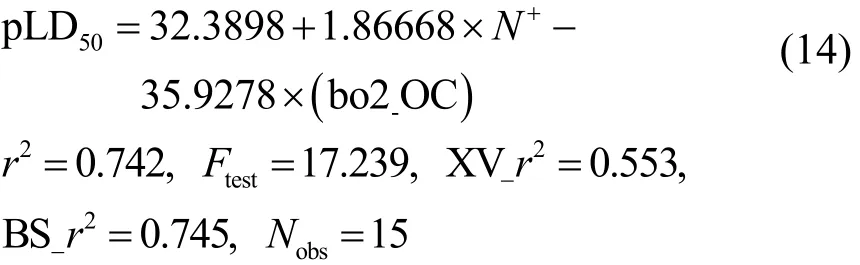
方程15 (MP2/gas):
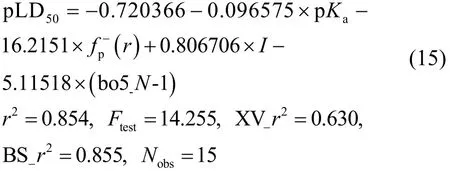
方程16 (MP2/water):

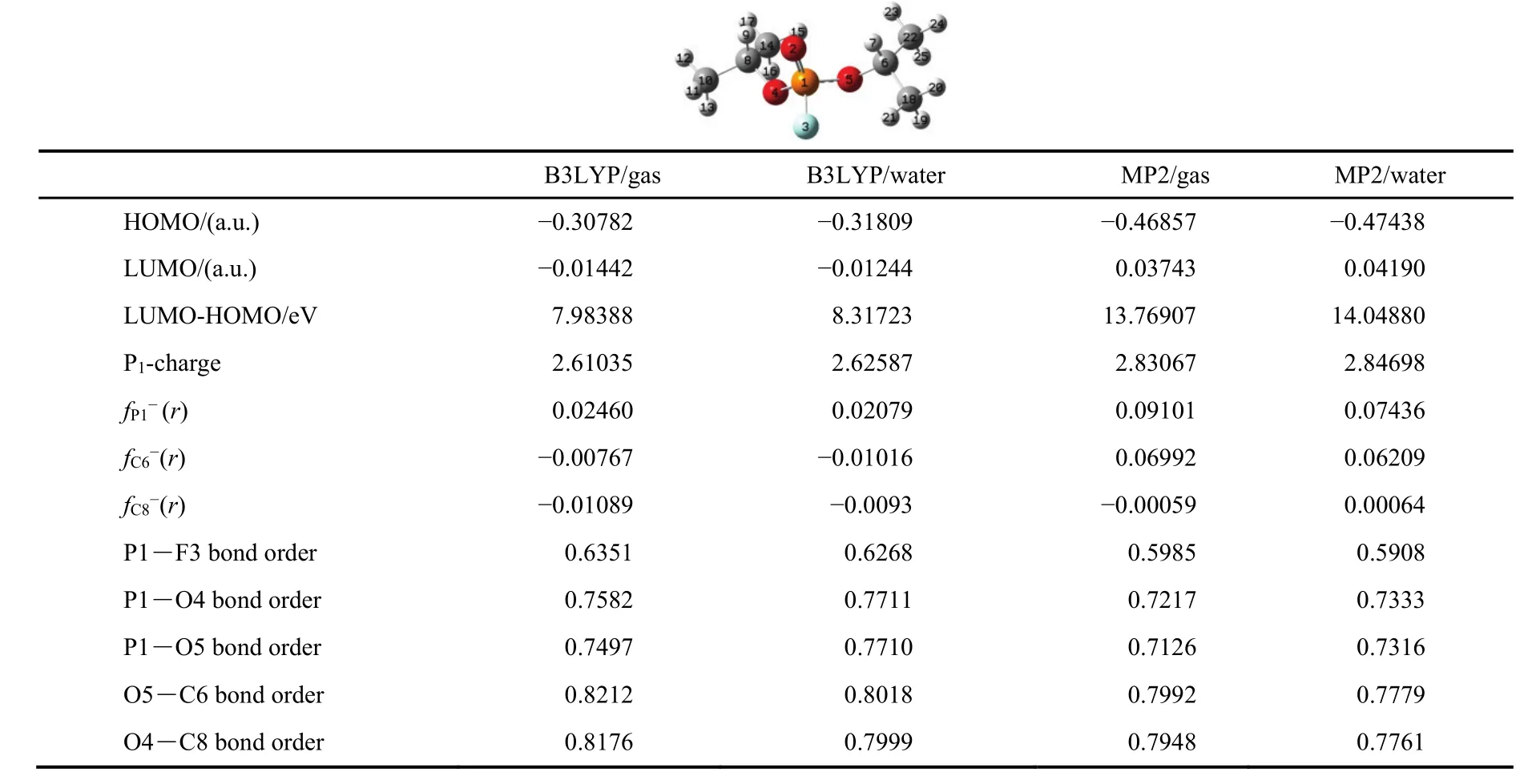
表4 二异丙基氟磷酸酯优化结构及四组条件的计算结果比较Table 4 Optimizing structure, atomic number of diisopropyl phosphofluoridate and comparison of calculation results with four different calculating level.
从前四个方程可以看出,B3LYP和MP2气相条件的计算结果要优于溶液相条件的结果,其原因可能是由于QSPR方程的毒性采用LD50,LD50反应的是所发生的反应在体内蛋白分子环境中进行,蛋白环境下的介电常数要远小于水环境,因此气相的计算结果更为可靠。且两个气相计算结果中,B3LYP/gas条件的计算结果更优于MP2得到的结果,其交叉验证相关系数XV_r2= 0.722,为四组条件的最佳结果。为了深入地比较分析,我们同时采用逐步回归方法,对相同计算参数下的 B3LYP/gas方法,氮非质子化形式计算的描述符进行了回归,得到了方程17。
方程17 (B3LYP/gas,氮非质子化):

方程17的决定系数和交叉验证相关系数等都有明显的下降,即采用氮的非质子化形式,相关性远不如采用氮的质子化形式。
同时,我们采用G/PLS统计回归方法,构建QSPR方程,通过变化主成分数和方程长度,合理地选择方程,并分别采用线性回归、样条函数回归、线性和样条函数的结合回归、非线性回归等多种方法进行统计分析。结果表明,直接采用线性回归,不如采用样条函数回归及线性和样条函数结合的回归获得的结果好;另外,因非线性回归的结果较差,故没有采纳。
3.3.2QSPR方程的pLD50预测
根据上述比较分析,我们选择方程13作为预测方程组的QSPR方程之一。同时,选择G/PLS方程中,满足 r2> 0.89; XV_r2> 0.83; BS_r2>0.89条件的10个方程组,共11个方程构成预测方程组,对含15个化合物的训练集和含6个化合物的测试集进行 pLD50的预测,其结果见表 5中Pred.1CDFT的预测结果,(详细参见 Supporting Informtion-S3)。
为了系统比较分析,我们同时采用Cerius2软件中的方法22,进行传统2D-QSPR参数计算、方程组构建与毒性预测,其结果见上表 5中 Pred.2 2D-QSPR的预测结果,(详细参见 Supporting Informtion-S3,其逐步回归方程18在表5注释中列出)。从逐步回归的2D-QSPR方程看出,r2= 1,且其 Ftest很大,出现显著的过拟合现象,显然不合理。从表 5可以看出,基于概念密度泛函方法的预测结果,明显优于采用常规的2D-QSPR方法,除化合物TEP的预测误差稍大外,其余三个化合物都相当不错;而常规的2D-QSPR方法有三个化合物的预测误差较大,只有一个化合物的预测结果较好。测试集中24-optfreq和27-optfreq化合物用这两种方法的预测结果具有显著地差别,CDFT方法预测结果毒性相对较高,而常规的2D-QSPR预测结果的毒性较低。但据文献报道26,这两个化合物是实验测定酶抑制活性logki最高的两个化合物,这与基于CDFT方法的预测结果基本吻合。
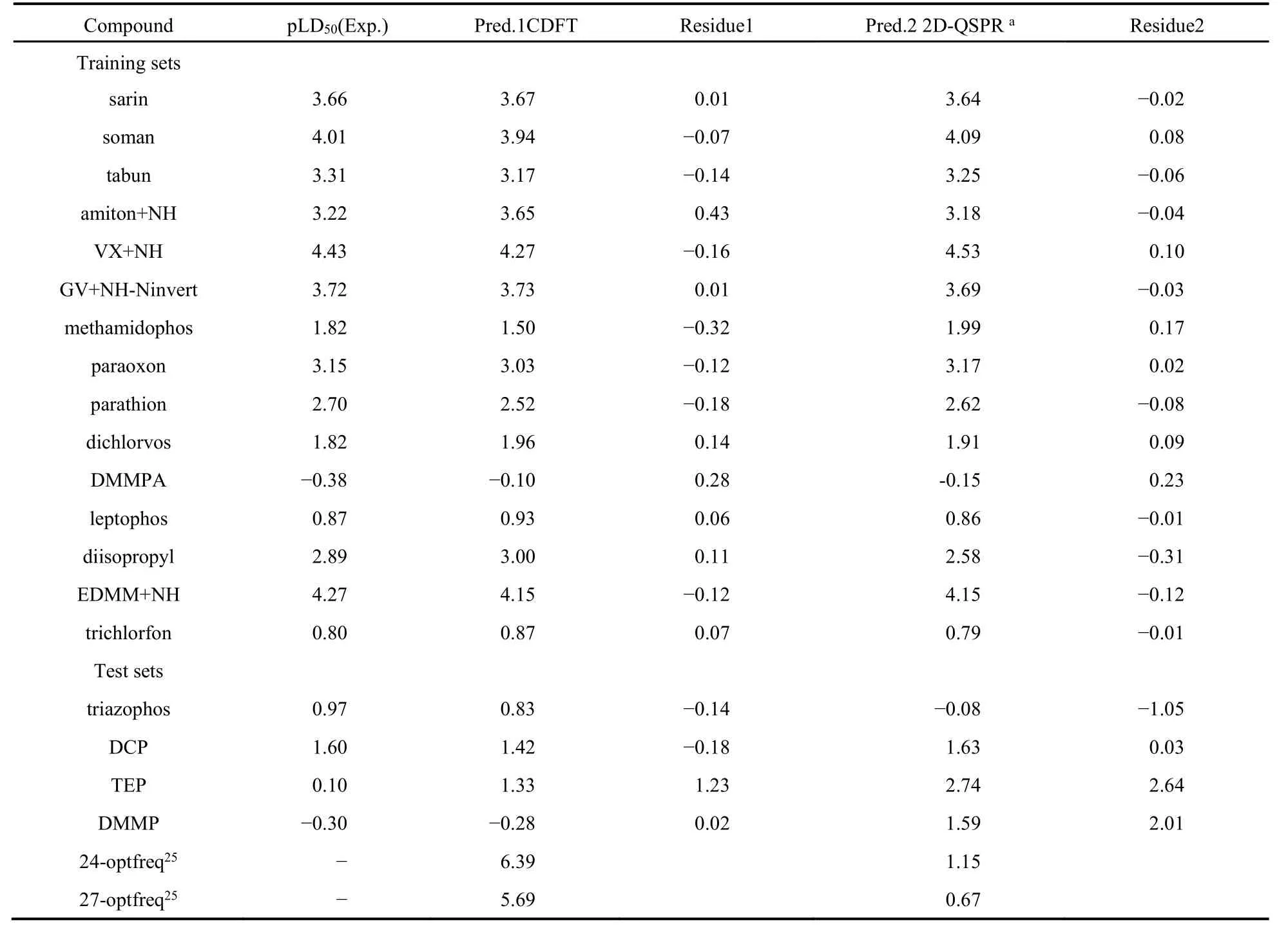
表5 根据CDFT和传统2D-QSPR方法,方程组对训练集和测试集化合物pLD50预测结果Table 5 pLD50 prediction results for the training set and the test set with the established equations average based on CDFT method and conventional 2D-QSPR.

根据以上研究,我们初步得出以下结果:离去基团乙胺基上氮的质子化形式是与乙酰胆碱酯酶相互结合的重要区域;以质子化形式进行该类分子的反应性指数理论计算和 QSPR方程构建是合理的。氮的质子化不仅增加一个受体负电区相互作用的结合点,同时增强了以磷原子为中心亲电进攻的反应性能;从对构象的敏感性和 QSPR方程的计算结果分析,B3LYP/6-311++G(2d,3p)/气相条件的结果更能准确地反应结构与毒性的差异,而MP2/6-311++G(2d,3p)的气相和水溶液相条件得到的结果,对反应性能的差异表现过于敏感,使得计算结果不稳定。
4 结论
通过对训练集和测试集化合物的反应性指数理论计算,QSPR方程组构建,以及外部测试集预测和交叉验证预测,我们发现应用基于概念密度泛函理论的化学反应性指数,进行乙酰胆碱酯酶不可逆抑制剂的毒性预测是完全可行的。研究结果表明:①大多数化合物的亲电进攻的反应中心发生在磷原子上,某些化合物的乙胺基氮原子上的质子化状态,能显著地增强磷原子的亲电性;②总的来看,构象对反应性描述指数的计算结果影响较小,但MP2方法有时对构象反应过分敏感,相似环境的原子计算值差别较大;③B3LYP/6-311++G(2d,3p)/gas条件得到的结果优于其它条件;④应用基于概念密度泛函理论的反应性描述指数构建的 QSPR模型,能够更准确地表达分子结构与毒性之间关系。
概念密度泛函方法提出的物理量具有明确的物理意义,能很好描述化学反应性的结构特点,因此越来越受到理论化学与(药物)应用化学家的广泛关注与重视。由于磷酸酯类反应性物质的高毒性,使得实验的危险系数高,数据资料不全或难以获得。所以采用计算机虚拟评估,应用构建的高精度 QSPR模型,预测未知化合物的毒性,是一个很好的选择。概念密度泛函理论在材料、药物化学等领域的QSA(T)R应用,仅在最近几年才略有文献报道,并有持续增长的趋势。本文将最新发展的量子力学概念密度泛函理论方法,应用于这类特殊反应性化合物的毒理性能评估和环境毒理评价,为减少动物的使用量,节约资源,降低环境污染等做一些努力。可望为探索磷酸酯类不可逆抑制剂与乙酰胆碱酯酶的作用机制开拓新思路,并为评估该类化合物的生态和环境毒性提供理论依据。
Supporting lnformation:available free of charge νia the internet at http://www.whxb.pku.edu.cn.
(1) Mekenyan, O. G.; Veith, G. D. SAR and QSAR in Εnνiron. Res.1994, 2, 129. doi: 10.1080/10629369408028844
(2) Katagi, K. Reν. Εnνiron. Contam. Toxicol. 2002, 175, 79.doi: 10.1007/978-1-4757-4260-2
(3) Karelson, M.; Lobanov, V. S. Chem. Reν. 1996, 96, 1027.doi: 10.1021/cr950202r
(4) Donald, M. M.; Karen, M. B.; Irwin, K.; Richard, E. S. Arch.Toxicol. 2006, 80, 756. doi: 10.1007/s00204-006-0120-2
(5) Ding, J. J.; Ding, X. Q.; Pan, L.; Chen, J. S. Acta. Phys. -Chim. Sin.2014, 30, 2157. [丁俊杰, 丁晓琴, 李大禹, 潘里, 陈冀胜. 物理化学学报, 2014, 30, 2157.] doi: 10.3866/PKU.WHXB201409171
(6) Ding, J. J.; Ding, X. Q.; Zhao, L. F.; Chen, J. S. Acta Pharm. Sin.2005, 40, 340. [丁俊杰, 丁晓琴, 赵立峰, 陈冀胜. 药学学报,2005, 40, 340.] doi: 10.3321/j.issn:0513-4870.2005.04.011
(7) Katritzky, A. R.; Kuanar, M.; Slavov, S.; Dennis Hall, C. Chem. Reν.2010, 110, 5714. doi: 10.1021/cr900238d
(8) Parr, R. G.; Yang, W. Annu. Reν. Phys. Chern. 1995, 46, 701.doi: 10.1146/annurev.pc.46.100195.003413
(9) John, C. H. J. Am. Chem. Soc. 2010, 132, 7558.doi: 10.1021/ja1030744
(10) Geerlings, P. K.; De Profit, F.; Langenaeker, W. Chem. Reν. 2003,103, 1793. doi: 10.1021/cr990029p
(11) Liu, S. -B. Acta Phys. -Chim. Sin. 2009, 25, 5. [刘述斌. 物理化学学报, 2009, 25, 5.] doi: 10.3866/PKU.WHXB20090332
(12) Bueno, P. R.; Miranda, D.A. Phys. Chem. Chem. Phys. 2017, 19,6184. doi: 10.1039/c6cp02504h.
(13) James, S. M. A.; Junia, M.; Paul, W. A. J. Chem. Theory Comput.2007, 3, 358. doi: 10.1021/ct600164j
(14) Pérez, P.; Yepes, D.; Jaque, P.; Chamorro, E.; Domingo, L. R.;Rojas, R. S.; Toro-Labbé, A. Phys. Chem. Chem. Phys. 2015, 17,10715. doi: 10.1039/c5cp00306g
(15) Domingo. L. R.; Ríos-Gutiérrez. M.; Pérez P. Molecules 2016, 21,748. doi: 10.3390/molecules21060748
(16) Chattaraj, P. K.; Roy, D. R. Chem. Reν. 2007, 107, PR46.doi: 10.1021/cr078014b
(17) Sablon, N.; Proft, F. D.; Ayers, P. W.; Geerlings, P. K. J. Chem.Theory Comput. 2010, 6, 3671. doi: 10.1021/ct1004577
(18) Tim, F.; Sablon, N.; Proft, F. D.; Ayers, P. W.; Geerlings, P. K.J. Chem. Theory Comput. 2008, 4, 1065. doi: 10.1021/ct800027e
(19) Semenyuk, Y. P.; Morozov, P. G.; Burov, O. N.; Kletskii, M. K.;Lisovin, A. V.; Kurbatov, S. V.; Terrier, F. Tetrahedron 2016, 72,2254. doi: 10.1016/j.tet.2016.03.024
(20) Ayers, P. W.; Parr, R. G. J. Chem. Phys. 2008, 128, 184108.doi: 10.1063/1.2918731
(21) http://www.drugfuture.com/toxic/search.aspx. (accessed March 28,2013).
(22) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb,M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.;Petersson, G. A.; et al. Gaussian 09, Revision B.04; Wallingford CT,Pittsburgh, PA: Gaussian Inc., 2009.
(23) Cerius2, Version 4.5; Accelrys Inc.: San Diego, CA 92121, USA,1999.
(24) ACD lab 12.0 software; Advanced Chemistry Development, Inc.:Canada, 2010.
(25) HyperChem7.0 (Beta1.04 for Evaluation copy) Software; Hypercube,Inc.: Gainesville, 2002.
(26) Victor, E. K.; Eugene, N. M.; Anatoly, G. A. QSAR & Comb. Sci.2009, 6-7, 664. doi: 10.1002/qsar.200860117
