结合零空间交与多播的K用户BC网络分析

王　越， 刘　锋， 曾连荪

(上海海事大学 信息工程学院， 上海 201306)

众所周知，通过采用多输入多输出(Multiple-Input Multiple-Output，MIMO)空间复用技术在多条独立的链路中传输不同的数据码流，可以成倍地提高数据的吞吐量．但是，使用多输入多输出技术的系统仍然受到消息之间的相互干扰，使得系统性能受到影响．对于无线网络系统的容量研究是十分困难的，因此考虑从另一个角度——自由度来衡量系统的容量大小．有关多输入多输出的单播网络研究已经非常多了，如广播信道(Broadcast Channel，BC)[1-3]、互扰信道(Interference Channel，IC)[4]、X信道(X Channel，XC)[5]等，但是有关多播网络的研究相对比较少．文献[6]提出多播的概念，并且导出网络的可达区域以及外界; 文献[7]提出的结合多播的模型改善了系统的频谱和能量效率; 文献[8]介绍了一种在移动系统中的多输入多输出多播和广播方案可伸缩视频编码的传输，可改善个人用户的信道质量．在多输入多输出网络中，自由度主要受到干扰的影响，尤其是多播网络，干扰消息主要来自网络内部和网络之间．因此，对多播网络的干扰处理并获得更大的自由度的研究是非常必要的．处理干扰的方法有很多种，如干扰中和、干扰对齐和迫零等，笔者提出并使用结合零空间交[9]的迫零方案来消除干扰．该方案的主要思想是: 针对多播网络的同一个接收端存在多个干扰消息，通过收发端合理的天线配置，使得多个干扰消息对应的零空间可以取得交空间，再将多个干扰消息同时置于这个交空间中，这样就可以使得干扰消息迫零，从而在接收端可以解码出期望信号．

在以往的研究中已经使用迫零方法得到了单播的广播信道、互扰信道、X信道等简单模型的自由度．然而对于更加复杂的多播信道的自由度，研究仍然较少．所以，笔者考虑将迫零方法引入到多播系统中，以便展开对多播理论的深入研究．

笔者主要研究的是多播的K用户广播信道网络的自由度，这是一种新的广播信道模型．不同于以往的简单单播广播信道模型，笔者提出的模型采用“循环模式”为每个接收端分配期望消息，同时，采用结合零空间交的迫零方案，将同一个接收端的多个干扰消息置于对应零空间的交空间中，以实现同时迫零多个干扰消息．

图1　K用户广播信道多播网络的系统模型

1　系统模型

K用户广播信道多播网络自由度研究的系统模型如图1所示．

系统模型的发送端发送K个消息，每个接收端均接收到K-N个期望消息和N个干扰消息．由于在每个接收端都存在N个干扰消息，所以要使用某种方法消除接收端的N个干扰消息．在这里，使用笔者提出的迫零方案——零空间交，使接收端的干扰消息全部迫零，以消除干扰消息．

对期望消息与干扰消息的简要说明: {W1，W2，W3，…，WK-1，WK}是发送端发送的K个消息．接收端1共收到K个消息，其中有K-N个期望信号，分别是{W1，WN+2，WN+3， …，WK-1，WK}，其他N个消息都是干扰消息; 接收端2共收到K个消息，其中有K-N个期望信号，分别是{W1，W2，WN+3，WN+4，…，WK-1，WK}，其他N个消息都是干扰消息; 其他接收端情况依此类推．

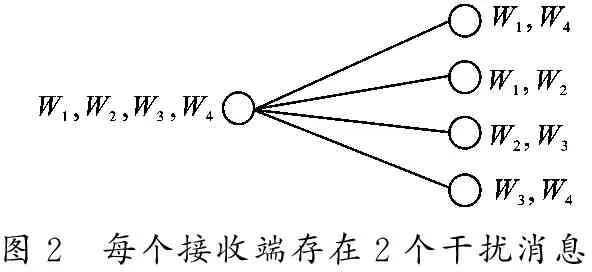
图2 每个接收端存在2个干扰消息

针对接收端信号采用“循环模式”: 对于发送端信号{W1，W2，W3，…，WK-1，WK}，将W1发送给从第1个接收端开始的共N个接收端;将W2发送给从第2个接收端开始的共N个接收端; 依此类推，即可得到笔者提出的“循环模式”系统模型．图2给出了一个采用“循环模式”的系统模型．

多播K用户广播信道网络的系统模型的输入输出关系为

Yj=HjX+Zj,

(1)

其中，Yj代表的是维度为(K-N)×1、第j(j=1，2，3，…，K)个接收端的输出信号;Hj代表的是发送端到接收端j、维度为 (K-N)×K的信道矩阵;X表示广播信道模型的发送信号;Zj表示 (K-N)×1 维信道的加性高斯白噪声．

对这种多播系统模型的自由度定义为多播网络系统的自由度就是系统接收端解码消息的总数．根据多播系统模型的自由度大小，可间接衡量系统的容量大小，也是判定系统模型性能优劣的一个重要指标．

2　方案分析与设计

针对上面提出的系统模型，采用了结合零空间交的迫零方案，分析如何从带有干扰消息的信号中解码出期望消息，同时得到系统的自由度大小．为了便于分析，先从4用户模型开始向一般模型过渡逐步分析．

2.1　4用户情况

2.1.1每个接收端存在2个干扰消息的情况

在图2中，发送端发送4个消息，每个接收端根据“循环模式”分别从发送的4个消息中接收2个期望消息，同时消除另外2个干扰消息．其中，发送端至少配置5根天线，接收端均配置2根天线．

该模型采用迫零方法来处理干扰消息，从而解码出期望消息．具体就是，接收端1有两个干扰消息W1和W4，只有2个期望信号W2和W3; 其他类似．设波束成形向量F= [f1,f2,f3,f4]5×4．该模型的输入输出关系满足式(1)．其中，Hk的维度为 2×5 ; 消息信号矩阵S的维度为 4×1．

要实现迫零某个干扰信号，只要将该干扰信号置于信道矩阵构成的零空间的交空间．针对当前模型来说，接收端3和4的干扰消息W1置于H3和H4构成的零空间的交空间中; 接收端1和4的干扰消息W2置于H1和H4构成的零空间的交空间中; 接收端1和2的干扰消息W3置于H1和H2构成的零空间的交空间中; 接收端2和3的干扰消息W4置于H2和H3构成的零空间的交空间中．

首先给出一个关于零空间交的引理，如下．

由上述引理可导出一条重要结论．若(m+p)×n矩阵C的秩r=rank(C)，则它的右奇异向量{ν1，ν2，…，νn}中，与n-r个零奇异值对应的右奇异向量{νr+1，νr+2，…，νn}构成零空间的交 null(A)∩ null(B)的标准正交基．若零空间的交存在，则必有n-r≥ 1; 而矩阵C是满秩的，有r= min(m+p，n)．由此可以得到关系式

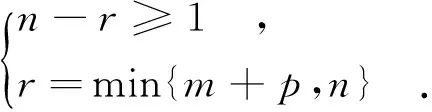
(2)

简化后得到零空间交的重要结论:n≥m+p+1． 再依据上述引理，可设Q1= [H3;H4]，Q2= [H1;H4]，Q3= [H1;H2]，Q4= [H2;H3]，维度均为 4×5，则波束成形向量满足:

fi∈null(Qi)．

(3)

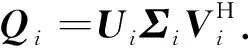
(4)

其中，Vij(i=1， 2， 3，4;j=5)表示取矩阵Vi的第5列．

通过上述简单分析，可以找到当前信道模型的波束成形向量，使得每个接收端的干扰消息迫零，同时可以得到当前模型的自由度为 2×4=8．

图3 每个接收端存在1个干扰消息

2.1.2每个接收端存在1个干扰消息的情况

在图3中，发送端发送4个消息，每个接收端根据“循环模式”分别从发送的4个消息中接收3个期望消息，同时消除1个干扰消息．其中，发送端至少配置4根天线，接收端均配置3根天线．

对于该情况，每个接收端只有1个干扰消息，不存在零空间交，可看成零空间交的退化情况．同样使用上一小节的方式迫零干扰消息，获得期望信号．同时，可得当前的4用户模型自由度为 4×3= 12．

2.2　K用户情况

上节主要分析了4用户模型，并给出了如何使每个接收端的干扰消息迫零，同时也指出了对应模型的自由度．考虑到实际工程中应尽量节省成本，依据上节提出的迫零方案，下面将针对更一般的K(K>3) 用户系统模型，分析如何最优配置天线以实现迫零干扰，同时简要分析一般模型的自由度大小．

2.2.1最优天线配置

K用户系统模型如图1所示．对于接收端，可以配置天线数量与期望信号数量相同，即每个接收端均配置K-N根天线．下面来分析发送端的天线数量的最优配置问题．

定理对于多播K用户广播信道网络，每个接收端都配K-N根天线，则使用结合零空间交的迫零方案，发送端至少配置NK- (N2-1) 根天线，即可在每个接收端收到K-N个期望消息，并迫零N个干扰信号，同时系统模型的自由度为 (K-N)K．

证明对于笔者提出的“循环模式”的系统模型，不妨从信道维度来分析天线的具体配置问题，并假设发送端至少配置L根天线，才可以实现在每个接收端获取对应的K-N个消息，同时消除N个干扰消息．已知Hi(i=1， 2， 3，…)表示发送端到接收端的信道矩阵，其维度用 (K-N)×L表示．

与4用户情况类似，在每个接收端要实现存在N个干扰消息的接收消息中获得K-N个期望消息，就必须将干扰消息置于对应信道矩阵的零空间交中．即接收端1至N的干扰消息W1置于{H1，H2，…，HN}构成的零空间; 接收端2至N+1 的干扰消息W2置于{H2，H3，…，HN+1}构成的零空间;以此类推．同时，可以确定对应信道矩阵的维度为N(K-N)×L．

再根据引理及其导出结论:n≥m+p+1，可以确定n和m+p表示上述零空间的维度，即n=L且m+p=N(K-N)，因此可以得出L≥N(K-N)+1．即得证当前模型的发送端最优天线配置为N(K-N)+1 根．又因为每个接收端均解码出K-N个消息，因此可以确定该系统模型的自由度为K(K-N)．

2.2.2干扰处理分析

上一小节已经详细分析了K用户模型的最优天线配置问题，接下来展开分析如何实现在接收端消除干扰，以便获取相应的期望消息．在这里采用迫零方案，关键在于将干扰消息同时置于多个信道矩阵构成的零空间中，实现将干扰迫零．具体的分析如下．

假设波束成形向量F=[f1，f2，f3，…，fK-1，fK]．将发送消息Wi(i=1， 2， 3， 4，…，K)看成干扰消息时，必然对应N个接收端将该消息视为干扰消息，将N个接收端对应信道矩阵组合起来，并用Q表示，形如Q= [H2;H3]．

对图1所示的模型，不妨用Q1表示干扰消息W1对应的组合信道矩阵．以此类推，可得到QK表示干扰消息WK对应的组合信道矩阵．从而得出波束成形的列向量与组合信道矩阵Qi(i=1， 2， 3， 4，…，K)之间的关系:

fi∈null(Qi)．

(5)

(6)

其中，m=N(K-N)+1，Vim表示取Vi(i=1，2，3，…，K)的第m列向量．

通过上述分析，可以找到使干扰消息迫零的波束成形向量F，进而每个接收端可以解码出期望消息，同时消除干扰消息．

2.2.3复杂度分析

依据前面的天线配置方案及干扰处理，在这里对系统的复杂度展开分析．根据矩阵理论可知: 对于秩为r的m×n的矩阵A，对A进行奇异值分解或求取广义逆，其复杂度均为O(mnr); 同时，对于m×n的矩阵A和n×p的矩阵B，两者相乘的复杂度为O(mnp)．

首先分析发送端的复杂度．构成零空间的组合矩阵的维度可从前面得知为N(K-N)×L，对该组合矩阵进行奇异值分解，可以得到为获得每个发送消息对应的波束成形向量的计算过程的复杂度为O(N(K-N)2L)，其中L就是发送端最低天线配置数量，即L取值N(K-N)+1．又因为该广播信道网络发送K个消息，因此发送端的总复杂度CT=O(KN(K-N)2L)，即

CT=O(KN(K-N)2(N(K-N)+1))=O(KN2(K-N)3)．

(7)

然后分析接收端的复杂度．在每个接收端通过使用HkF的广义逆实现线性编码方案，其中Hk的维度为 (K-N)×L，F的维度为L×K．首先，Hk与F相乘的复杂度为O((K-N)LK)，再对HkF进行广义逆计算，其复杂度为O(K(K-N)2)．因此，每个接收端的总复杂度CR=O((K-N)LK)+O(K(K-N)2)，即

CR=O(KN(K-N)2+K(K-N)2)=O(KN(K-N)2)．

(8)

对于整个广播信道网络而言，总的系统复杂度C=CT+CRK．将式(7)和式(8)代入，并经过整理之后，可以得到

C=O(KN2(K-N)3+K2N(K-N)2)=O(KN2(K-N)3)．

(9)

整个多播广播信道网络总的系统复杂度如式(9)的结论．

3　仿真与分析

依据前面的方案分析，在本节使用了Matlab对广播信道网络模型进行了仿真分析．假设每个信道为不相关的瑞利衰落信道，发送端的发送功率为P，发送端在满足总的功率限制下，对每个用户的发送功率平均分配，每个用户接收端噪声方差都相同且设为σ2．同时，假设发送端可获知它所发送的所有用户的无差错等效信道状态信息，每个用户同样可获知接收端到发送端的信道状态信息．

用户i的消息经过一列处理之后，在接收端的接收信噪比为

RSINRi=Pe/(σ2+Pi),

(10)

其中，Pe表示每个接收端的期望消息功率，Pi表示每个接收端的干扰消息功率．用户i的期望消息的速率为

Ri=lb(1+RSINRi)．

(11)

因此，可以得到系统的总和速率为

(12)

依据上述对和速率的分析，可以对系统的和速率[10]进行分析，并得到仿真结果，如图4和图5．

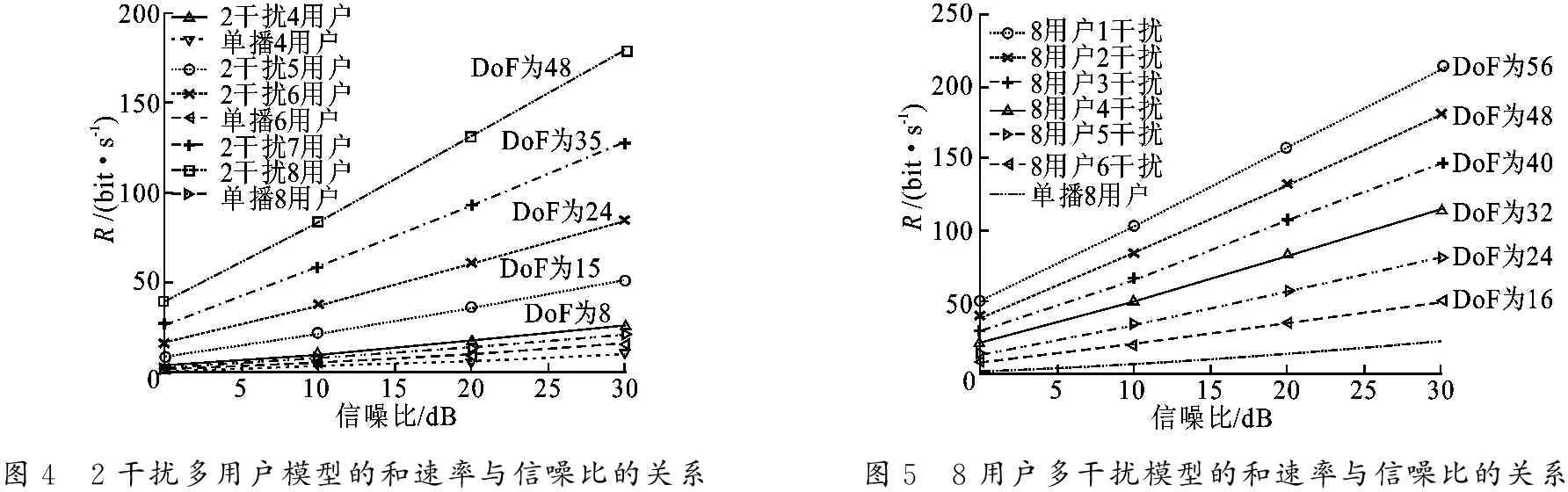
图4 2干扰多用户模型的和速率与信噪比的关系图5 8用户多干扰模型的和速率与信噪比的关系

图4描述的是每个接收端均有2个干扰消息的多用户系统的和速率与信噪比之间的变化关系．当用户数从4增加到8时，系统的自由度相应地从8增加到48．从图中可以看出，在固定每个接收端的干扰消息数量N的情况下，系统自由度随着用户数K增加而增加，并且仿真结果与理论结果一致．

图5描述的是8用户多干扰消息的系统的和速率与信噪比之间的变化关系．当每个接收端的干扰消息数量相同且从1个增加到6个干扰消息时，对应的自由度大小从56减少到16．从图中可以看出，在固定用户数的情况下，系统自由度随着干扰消息数N增加而线性减少．这个结果同样与理论结果一致．

图4和图5中还描述了单播多用户的和速率随着信噪比的变化关系．从图中可以看出，在相同信噪比条件下，多播广播信道网络的和速率明显高于单播广播信道网络的．

对比两幅图不难得出，如果期望获取更大的系统自由度，可以从两个角度考虑问题:控制用户数量，使其尽量得多;控制每个接收端的干扰消息数量，使其尽可能得少．

4　结 束 语

笔者尝试采用以零空间交为基础构造一种新的对干扰消息迫零方案，研究了多播的K用户广播信道网络模型．与常见单播广播信道网络模型相比较，笔者提出的模型具有更高的系统性能和速率．同时，笔者提出的模型采用“循环模式”的天线配置方式，使接收端的干扰消息数量可控，从而可给出一般化模型的统一的最优天线配置方案．在结合迫零方法和天线配置方案的基础上，证明了笔者提出的模型的正确性及方案的可行性，并针对这种模型进行了仿真分析，验证了理论与实际结果的一致性．同时，该迫零方案也可应用于每个接收端的干扰消息数量不等的模型，这部分内容可单独深入研究．下一步的工作可将本方案应用于其他系统中，如用户数量与发送消息数量不等的多播广播信道系统，或多播互扰信道系统，或多播X信道系统，以便更深入地研究多播问题．

参考文献：

[1] YANG M H, JEON S W , KIM D K. Linear Degrees of Freedom of MIMO Broadcast Channels with Reconfigurable Antennas in the Absence of CSIT[J]. IEEE Transactions on Information Theory , 2017, 63(1): 320-335.

[2]李钊, 杨家玮, 姚俊良, 等. 采用独立分量分析的多用户MIMO下行传输策略[J]. 西安电子科技大学学报, 2010, 37(2): 192-196.

LI Zhao, YANG Jiawei, YAO Junliang, et al. Multiuser MIMO Downlink Transmission Strategy Using Independent Component Analysis[J]. Journal of Xidian University, 2010, 37(2): 192-196.

[3]RASSOULI B, HAO C, CLERCKX B. DoF Analysis of the MIMO Broadcast Channel with Alternating/Hybrid CSIT[J]. IEEE Transactions on Information Theory, 2016, 62(3): 1312-1325.

[4]GOU T, JAFAR S A. Degrees of Freedom of theKUserM×NMIMO Interference Channel[J]. IEEE Transactions on Information Theory, 2010, 56(12): 6040-6057.

[5]JAFAR S A, SHAMAI S. Degrees of Freedom Region of the MIMO X Channel[J]. IEEE Transactions on Information Theory, 2008, 54(1): 151-170.

[6]ZAMANIGHOMI M, WANG Z D. Degrees of Freedom Region of Wireless X Networks Based on Real Interference Alignment[J]. IEEE Transactions on Information Theory, 2016 , 62(4): 1931-1941.

[8]CHOI Y I, KANG C G. MIMO Transmission Scheme for Scalable Video Broadcast and Multicast Service[C]//Proceedings of the 2016 International Conference on Information and Communication Technology Convergence. Piscataway: IEEE, 2016: 365-367.

[9]张贤达. 矩阵分析与应用[M]. 2版. 北京：清华大学出版社, 2013: 601-613.

[10]YANG Z, CUI J J, LEI X, et al. Impact of Factor Graph on Average Sum Rate for Uplink Sparse Code Multiple Access Systems[J]. IEEE Access, 2016, 4: 6585-6590.