On the generation of drift flows in wall-bounded flows transiting to turbulence Paul Manneville*

Generically the transition to turbulence in flows along solid walls, so-called wall-bounded flows, can be triggered at Reynolds numbers well below the value at which the laminar base flow profiles are linearly unstable [1, 2]. The existence of nontrivial solutions to the Navier-Stokes equations (NSEs) competing with the stable base flow, is believed to be well understood in terms of self-regenerating coherent structures [3]. The corresponding process, called SSP [3, 4], involvesstreamwise vorticesinducingstreamwise streaksby lift-up, the so-produced mean flow distortion being subsequently unstable in a way that closes the cycle by feeding the vortices present at start. At least at the moderate Reynolds numbers where the transition to turbulence takes place, this plausible general sequence has a high degree of applicability.

Such nontrivial flow regimes arise from saddle-node bifurcations in state space but their coexistence with laminar base flow has also to be appreciated in physical space. An important feature of transitional planar or nearly planar wall-bounded flows is indeed the separation of the full space into turbulent and laminar regions separated by sharp fluctuating interfaces, in the form ofturbulent spotsnear the global stability thresholdand more complicated laminar-turbulentpatternsat larger values of the Reynolds number. Formally, this can be understood as resulting from a modulation in space of the strength of the SSP mechanism, active in turbulent domains and switched off in the surrounding laminar flow. This modulation of the mechanism's intensity is in general detectable up to a limit above which a regime of uniform turbulence calledfeatureless[5] is recovered.The transition from modulated to featureless turbulence may then be marked by a well-defined threshold usually denoted,and laminar-turbulent coexistence be observed in an intervalof finite width. For example, in plane Couette flow (PCF,the shear flow between counter-translating parallel plates at distanceand relative speed, for which), the transitional range extends fromtoand a periodic modulation of the turbulence intensity is observed in the form of bands alternatively laminar and turbulent, oblique with respect to the streamwise direction [2, 6].

Both around turbulent patches or between turbulent bands,near-laminar flow is the superposition of the base flow and large scale corrections believed to play an important role in the overall structure of turbulence [7]. These corrections have components that do not average to zero in the wall-normal direction,which makes them capable of transporting coherent structures as a whole, subsequently acting on oblique spot growth [8, 9].For that reason, they will be calleddrift flowsin the following.Oblique growth and the oblique laminar-turbulent organization clearly break the original spanwise symmetry of the problem statistically restored beyond. The aim of this note is to bring hints on the origin of these flows and their relation to symmetry breaking at a local level, i.e. the minimal flow unit (MFU), the scale introduced by Jiménez and Moin [10] below which coherent structures with sizable lifetimes are no longer observed. The MFU is defined in the context of numerical simulations with wall-parallel periodic boundary conditions at distancesandtypically of the same order of magnitude as the wall-normal characteristic size, viz. the gapfor PCF. It is the privileged scale at which transitional coherent structures are studied [11]and arguments from dynamical systems and chaos theory are developed [12].

Great progress in the understanding of the SSP has been obtained thanks to Waleffe [4] who built an analytical, relatively simple, model accounting for it within the MFU framework,called WA97 in the following. It was obtained as a first-harmonic truncation of a Galerkin expansion of the NSEs with stress-free boundary conditions in a plane Couette-like geometry, sometimes calledWaleffe flow[13]. A straightforward analysis using trigonometric basis functions yielded WA97 as a system of 8 differential equations governing 8 mode amplitudes that was next reduced to a 4-dimensional system, the one studied in greatest detail. The four amplitudes retained were explicitly associated to a mean flow distortion, the streaks and vortices amplitudes and the amplitude of a combined mode effective in closing the system appropriately. By construction WA97, whether reduced or not, preserves the spanwise symmetry of the flow configuration.My purpose will be to generalize Waleffe's approach to allow for drift flows observed in numerical simulations [8] or experiments[9]. In some sense, this can be viewed as an analytical counterpart to the numerical approach developed by Kreilos et al. [14]who studied drifting patterns at MFU size in related transitional flows.

The Galerkin approach to be used is a weighted-residual method analyzing the problem at hand by expanding its fields and governing equations onto functional bases. When pushed at high orders, it can serve as a numerical simulation method with good convergence properties [15]. It is however usually not developed as such in computational fluid dynamics and alternate methods are used, e.g. [16], more straightforward but rather working as black-boxes not amenable to analytical developments. Here, the aim is therefore not to apprehend theabstractstructure of state space within the MFU framework in detail through the accurate determination of exact solutions to the NSEs like in Ref. [11]. On the contrary, and much in the spirit of Waleffe's seminal work [4], I will attempt to uncover theconcretelocal source of mean-flow corrections involved in the symmetry breaking typically observed at transitional values of. To this aim, I will consider the Galerkin method rather as a systematic reductive modeling strategy of the primitive equations, achieved by truncating the expansion at the lowest possible but still significant order, so low that it can still be handled analytically while clear physical significance can be given to the mode amplitudes retained.

In accordance with the wide generality of the SSP for the base flows of interest, systems with similar structures can be derived with differences only appearing in the value of the coefficients.Since trigonometric relations between the basis functions used to deal with the stress-free boundary conditions for Waleffe flow[4] artificially kill some nonlinear interactions, in order to work with a slightly less restrictive case, I will consider standard PCF driven by no-slip conditions at the plates. On another hand, I will follow Waleffe in his restriction to a first-harmonic approximation of the MFU dynamics to describe the wall-parallel periodic dependence of the state variables. A cursory presentation of the model, the full expression of which is developed in the Appendix, is first given. Its main properties are then discussed before some perspectives on laminar-turbulent patterning in transitional wall-bounded flow are presented from a more general standpoint.

The modeling approach starts from the velocity-vorticity formulation of the NSEs written for the perturbation to the base flow as detailed in Ref. [18], p.155. Though the wall-normal and wall-parallel directions can be treated simultaneously in the Galerkin approach as originally done by Waleffe [4], here I will first deal with the wall-normal direction making use of results in Refs. [19, 20], and next with the wall-parallel direction and the periodic conditions corresponding to the MFU definition. Simulations of PCF have shown that a representation of the flow at lowest significant order contains about 90% of the perturbation energy for transitional Reynolds numbers[21, App.B], accordingly I will just consider the corresponding minimal functional set, like for WA97:

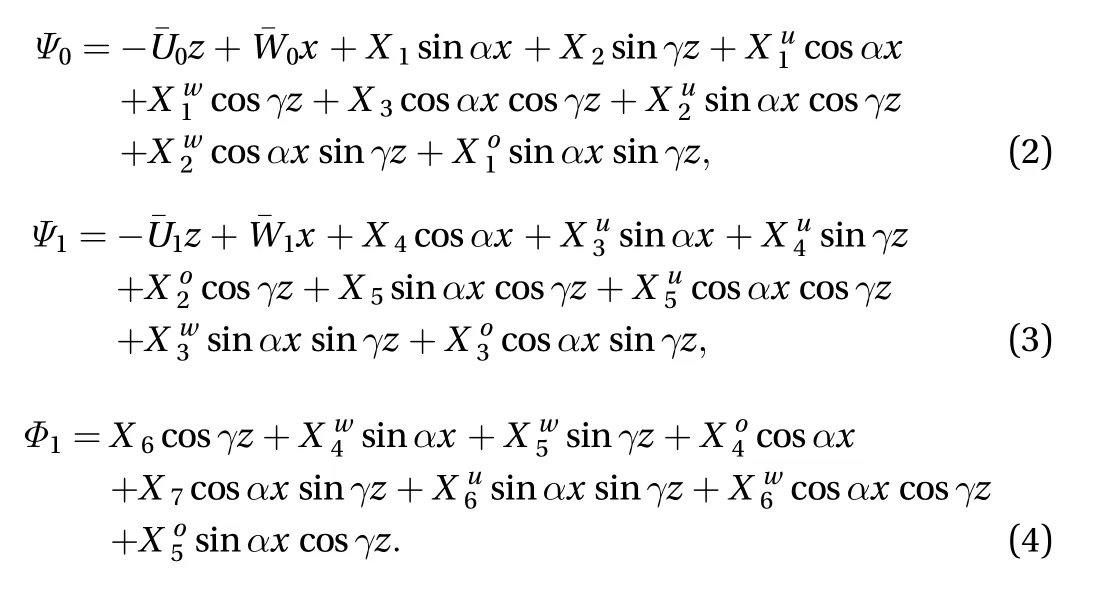
The velocity components are retrieved from the expression of the streamfunctionsand velocity potentialthrough:

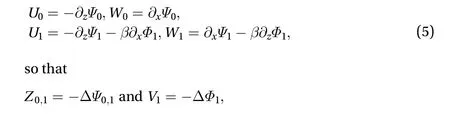
A set of 28 equations for the 28 unknowns is obtained by mere separation of harmonics. It displays all the properties, liftup, viscous dissipation, quadratic advection nonlinearities, linear stability of the base flow, expected from NSEs for wallbounded shear flows within the MFU framework. It formally reads:

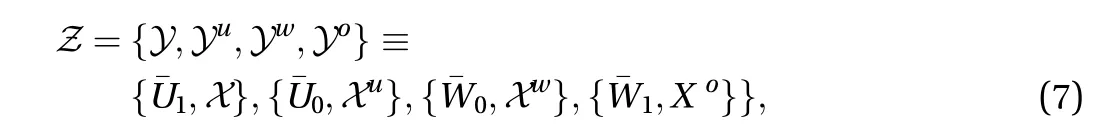
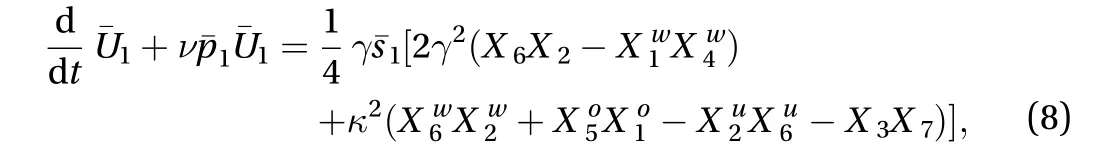
My second sample is Eq. (A.26) governing, a spanwise mean flow correction absent from WA97:

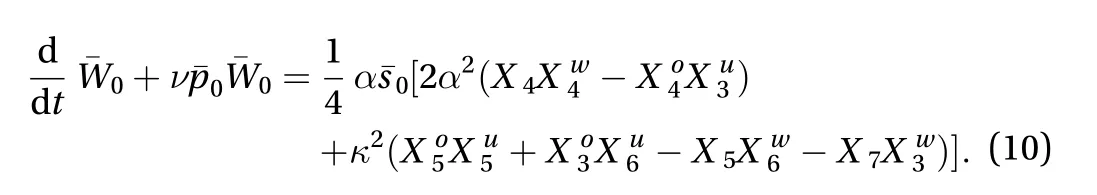
The two last equations in this group, Eq. (A.25) forand Eq.(A.28) for, follow the same simple pattern. The third sample is Eq. (A.2), the equation governing thestreakamplitude:

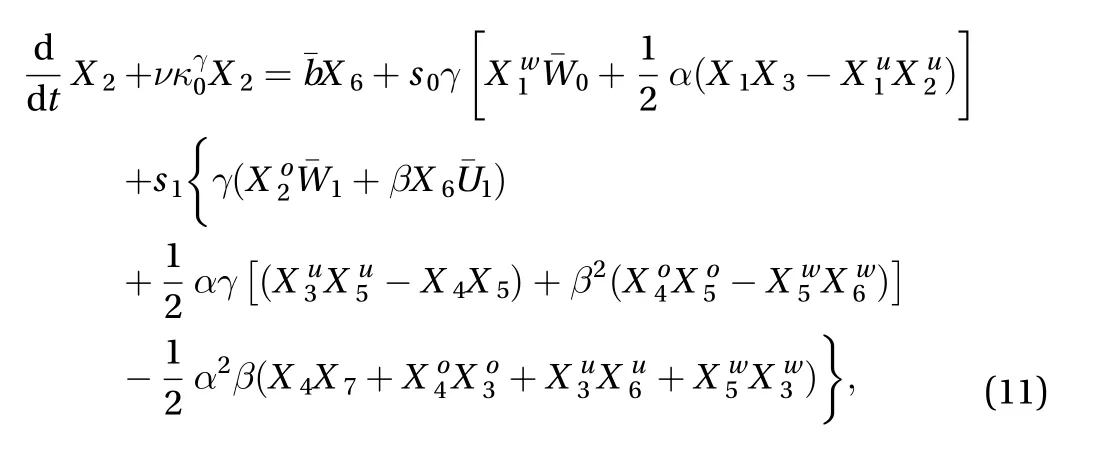
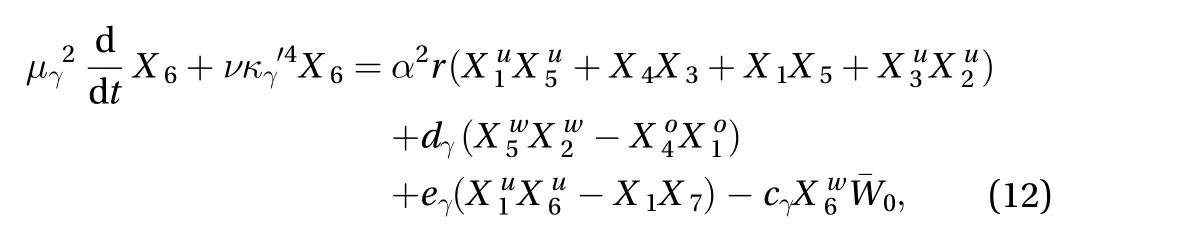
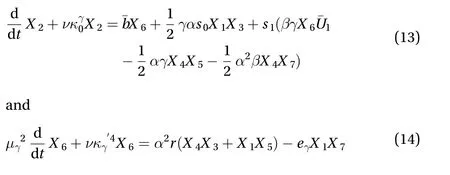
strictly corresponding to Waleffe's equations (10-2) and (10-3).When comparing his system to the corresponding one extracted from Eqs. (A.1)-(A.28), a single difference appears in Eq. (A.9) forthat reads

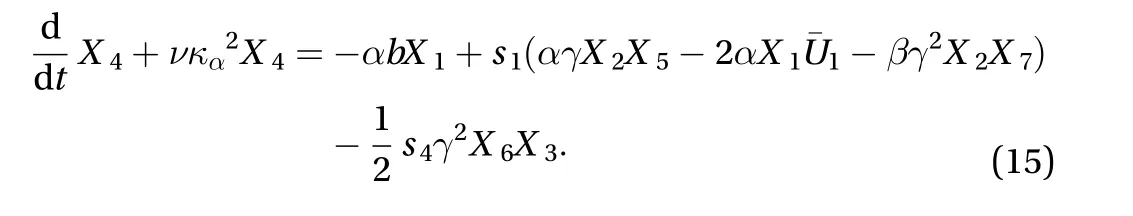
In WA97,is variableand the corresponding equation is Waleffe's equation (10-6) with the same terms as in Eq. (15) but lacks the last one,, i.e., that disappears owing to an accidental cancellation from trigonometric relations as noticed earlier. The detailed consequences of this observation have however not been scrutinized in detail.

Before considering the virtues and limitations of model Eq.(6), let me stress that, within the 1st-harmonic MFU assumption,its expression and detailed structure are quite general so that its applicability is not restricted to PCF or Waleffe flow. On the contrary, it should rather be understood as implementing the SSP on an extended footing that includes drift flows.

More importantly, the choiceis associated with specific spatial resonances between the different flow components. This resonance condition can be retrieved in each and every solution to the full system, whatever its time dependence, by performing an arbitrary time-independent translation,. Similar observations have been made in the literature, see Ref. [14] and references quoted. Here I will take a down-to-earth but instructive viewpoint and first note that this implies relations between the equations of the full system.For example, a translation byamounts to performing the changesand, which straightforwardly explains the similarity of equations forand,Eqs. (A.1) and (A.3),and, Eqs. (A.5) and (A.6), etc. with identical coefficients and signs modifications linked to the minus sign in the second change. An immediate consequence is that the dynamics restricted tois also closed. The case of-translation can be treated in the same way,showing that the subspaceis similarly invariant. Inspecting the full expression of Eqs. (A.1-A.28) finally shows that the subspaceis also invariant but with no obvious relation to translational properties.

On general grounds, the knowledge of the structure of phase space takes advantage of the stability properties of solutions known. As a consequence of the identification of invariant subspaces above and the quadratic nature of the nonlinearities, it follows from standardlinear analysis that the stability operator around a solution in has a block diagonal structure. The firstblock accounts■ for th■estability of the solution as if the system was restricted to, as dealt with in Ref. [4]. It corresponds toamplitudeperturbations. The two nex■tblocks a■re for infinitesimal perturbations living inand. These subspaces being associated with translations as discussed above, the related linear modes correspond tophaseperturbations.

For example, let us consider the effect of an infinitesimal translationon an arbritrary solution.At leading order the solution readswithwith. The components ofare,,,,,, and. It is indeed readily checked that the right hand side of Eq. (A.18) governingcancels identically for such a perturbation, which implies. Next forthat the right hand side of Eq. (10) also van-In addition, the equations governing all the non-zero components ofare identical to the equations for the corresponding component ofapart from appropriateof perturbationin Eq.

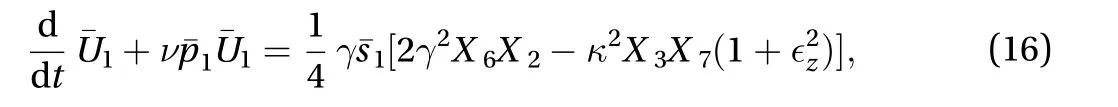
which shows that the dynamics ofis preserved at leading order. Accordingly, perturbations corresponding to an infinitesimal-translation are neutral and do not generate drift flow, as expected. The same argument can be developed for infinitesimal streamwise translations, with identification of theand proof of the absenceHowever, perturbations along the so-obtained eigenvectorsand, while neutral, are extremely special and it is immediately seen that arbitraryexpected to generate some non trivial drift flow. It suffices to look at Eq. (10), for convenience rewritten by dropping all irrelevant higher order terms as:

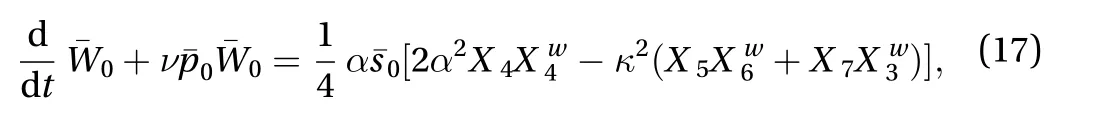
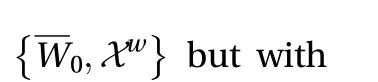
Periodic boundary conditions inherent in the MFU assumption maintain the fiction of a solution that would be uniformly developed in space. In actual systems with wall-parallel dimensions much larger than the wall-normal scale, itself typical of the size of the MFU, the intensity of the SSP can be modulated, especially in the turbulent spot regime aroundwhere the turbulence level varies from 0 to 1 in space, and in oblique banded laminar-turbulent patterns up to. In the stability analysis sketched above, spanwise and streamwise translations could be treated separately. This is no longer the case more generally since the corresponding drift flows are coupled by the continuity equation, an important condition at the heart of the Duguet-Schlatter argument about the obliqueness of laminar-turbulent interfaces [8], here expressed as [19]:

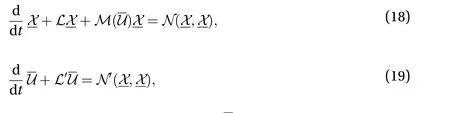
highlighting the origin and role ofU.

When dealing with modulations, we have to face the difficulty that, owing to the sub-critical character of transition, there is no systematic multiscale approach available. Nontrivial solutions emerge abruptly and steep interfaces in physical space separate different flow regimes, in sharp contrast with the case of supercritical bifurcations as pointed out by Pomeau [22]. The first reason is that there is no linear marginal stability condition to work with: the coherence length that controls the diffusion of modulations near threshold is indeed directly obtained from its curvature at the critical point. The second reason is that supercriticality implies a controllable saturation of the solution's amplitude. Both circumstances permit a rigorous and systematic perturbation approach [23, Chaps. 8-10], and none holds in the present case.

The spatial coexistence of laminar and turbulent flows is particularly difficult to apprehend from the primitive equations. An approachviaanalogical modeling in terms of reaction-diffusion(RD) systems [24], developed by Barkley [25, 26], has been particularly fruitful to account for the transitional range of pipe flow.In that model, the production of turbulence was considered as the result of a reaction and diffusion was introduced phenomenologically to treat the spatial coexistence of the two states, laminar or turbulent. Soon after the earliest developments of that work, I used the same RD framework but in the context of a Turing instability, i.e. a pattern-forming mechanism controlled by diffusion rates with sufficiently different orders of magnitude[24]. In my model [27], the local reaction terms were expressed using the reduced (4-dimensional) WA97 model [4], while its variables were allowed to diffuse with widely different turbulent viscosities in one direction of space. As a result, a Turing bifurcation was obtained at decreasing, defining a thresholdbelow which a pattern was present down to somecorresponding to a general breakdown toward laminar flow. Whereas it seems reasonable to use the variables into treat turbulence production at a local scale, the structure of Eqs. (18, 19) clearly shows that the simple heuristic assumption of a diffusionviaturbulent viscosities is unable to properly render the possible role of drift flows on pattern formation. On the other hand, a model equivalent to the spatiotemporal Galerkin system described in the Appendix was numerically studied by Lagha and myself in Ref. [28]. Filtering out the small scales, we could next determine the dynamic(s of larg）e-scale flows, in particular their drift-flow componentaround turbulent spots. They were obtained analytically as a response to Reynolds stresses given from the outside, not as stemming from some local dynamics possibly obtained within a MFU framework as examined here.

We can therefore infer that a combination of the two approaches, small scale dynamics including the feedback of large scales flows, should provide a satisfactory, now self-contained,description of laminar-turbulent coexistence in the transitional regime. Numerical simulations of Galerkin models truncated at different levels however suggest that the lowest nontrivial, threefield, level is insufficient to recover an organized laminar-turbulent band pattern, for PCF [20] as well as for Waleffe flow [13],and that we are requested to consider at least seven fields in order to obtain oblique bands in arange of finite width[20]. Working with a higher level model at the MFU scale, further incorporating the effect of space modulations, and of course simplifying the cumbersome so-obtained model appropriately,e.g. through adiabatic elimination of fast variables, is likely the only way to really explain the occurrence of laminar-turbulent pattern analytically. A RD picture [25-27] would emerge, mostly directed at the understanding of the transition from featureless turbulence to banded turbulence atupon decreasing. It would be derived from the NSEs and would replace the naive introduction of turbulent viscosities by a clean account of drift flows, hopefully containing the mechanism for a Turing instability. The approach is not limited to PCF or Waleffe flow and should provide a generic interpretation to laminar-turbulent coexistence in the transitional range for a wide range of wallbounded flows of practical interest, as can be anticipated from the universal structure of Galerkin approximations to the NSEs,the relevance of the SSP in producing nontrivial states already at the MFU scale and moderate Reynolds numbers, and the ubiquitous presence of drift flows.

I would like to thank Profs. G. Kawahara and M. Shimizu(Osaka University, Japan) and Dr. Y. Duguet (Computer Science Laboratory for Mechanics and Engineering Sciences (LIMSI),France) for discussions related to this work within the framework of the TransTurb JSPS-CNRS exchange program.

Appendix

Galerkin three-field modelAs explained in the text, we model PCF by severely truncating a Galerkin expansion of the no-slip problem starting with the velocity-vorticity formulation of Navier-Stokes equations written for the perturbation to a general streamwise laminar base flow[18]. These equations read:

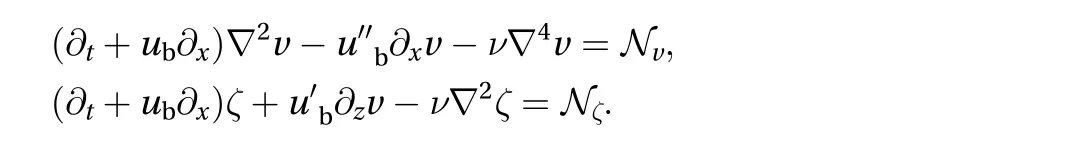
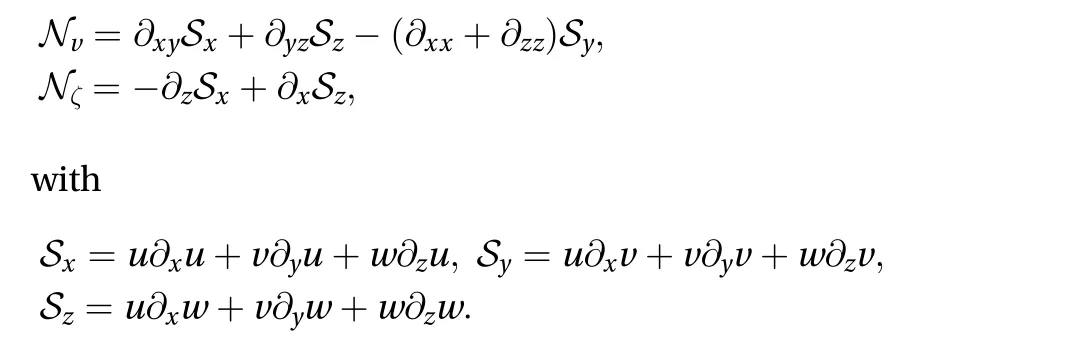
The perturbation velocity field is then expanded onto a convenient orthonormal polynomial basis as explained in Ref. [20]from which extract the lowest-order consistent set:

For linear terms:

?

from which it can be seen that the velocity profile of the stressfree case is much less dissipative than the no-slip profile as expected owing to the absence of boundary layers close to the walls.

For nonlinear terms:

?

Minor differences with coefficients given in Ref. [19] may be noticed, all stemming from the fact that we use the velocityvorticity formulation of Ref. [20] rather than the Navier-Stokes equations in primitive variables and a subsequent treatment of the pressure field in Ref. [19].

First-harmonic approximation in the MFU contextwall-normal vorticity components deriving from these fields read:

U0=¯U0-∂z~Ψ0，W0=¯W0+∂x~Ψ0，

U1=¯U1-∂z~Ψ1-β∂xΦ1，V1=-ΔΦ1，W1=¯W1+∂x~Ψ1-β∂zΦ1

Z0=∂zU0-∂xW0=-Δ~Ψ0，Z1=∂zU1-∂xW1=-Δ~Ψ1，

The model involves wave-vectorsandas parameters,andbeing the wall-parallel dimensions of the MFU. The first-harmonic guess reads (2-4). The velocity and

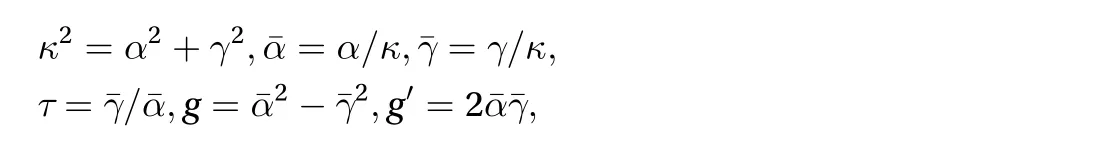
Equations have been derived using MATHEMATICA.

Equations stemming from the dynamics of

[1]S. Grossmann, The onset of shear flow turbulence, Rev. Mod.Phys. 72 (2000) 603–618.

[2]P. Manneville, Transition to turbulence in wall-bounded flows:Where do we stand?, Mech. Eng. Rev. Bull. JSME 3 (2016) 15-00684.

[3]J. Hamilton, J. Kim, F. Waleffe, Regeneration mechanisms of near-wall turbulence structures, J. Fluid Mech. 287 (1995)317–348.

[4]F. Waleffe, On a self-sustaining process in shear flows, Phys.Fluids 9 (1997) 883–900.

[5]C. Andereck, S. Liu, H. Swinney, Flow regines in a circular Couette system with independently rotating cylinders, J. Fluid Mech. 164 (1986) 155–183.

[6]A. Prigent, G. Grégoire, H. Chaté, O. Dauchot, Long-wavelength modulation of turbulent shear flows, Physica D 174 (2003)100–113.

[7]D. Barkley, L. Tuckerman, Mean flow of turbulent-laminar patterns in plane Couette flow, J. Fluid Mech. 576 (2007) 109–137.

[8]Y. Duguet, P. Schlatter, Oblique laminar-turbulent interfaces in plane shear flows, Phys. Rev. Lett. 110 (2013) 034502.

[9]M. Couliou, R. Monchaux, Growth dynamics of turbulent spots in plane Couette flow, J. Fluid Mech. 819 (2017) 1–20.

[10]J. Jimenez, P. Moin, The minimal flow unit in near wall turbulence, J. Fluid Mech. 225 (1991) 213–240.

[11]J. Gibson, J. Halcrow, P. Cvitanović, Equilibrium and travellingwave solutions of plane Couette flow, J. Fluid Mech. 638 (2009)243–266.

[12]G. Kawahara, M. Uhlmann, L. van Veen, The significance of simple invariant solutions in turbulent flows, Ann. Rev. Fluid Mech. 44 (2012) 203–225.

[13]M. Chantry, L. Tuckerman, D. Barkley, Turbulent-laminar patterns in shear flows without walls, J. Fluid Mech. 791 (2016) R8.

[14]T. Kreilos, S. Zammert, B. Eckhardt, Comoving frames and symmetry-related motions in parallel shear flows, J. Fluid Mech.751 (2014) 685–697.

[15]B. Finlayson, The method of weighted residuals and variational principles, with applications in fluid mechanics, heat and mass transfer, Academic Press, 1972.

[16]J. Gibson, Channelflow: a spectral Navier-Stokes simulator in C++, Tech. rep. , Georgia Institute of Technology (2008).http://www.Channelflow.org

[17]P. Schmid, D. Henningson, Stability and transition in shear flows, Springer, 2001.

[18]M. Lagha, P. Manneville, Modeling transitional plane Couette flow, Eur. Phys. J. B 58 (2007) 433–447.

[19]K. Seshasayanan, P. Manneville, Laminar-turbulent patterning in wall-bounded shear flows: a Galerkin model, Fluid Dyn. Res.47 (2015) 035512.

[20]P. Manneville, On the transition to turbulence of wall-bounded flows in general, and plane Couette flow in particular, Eur. J.Mech. B/Fluids 49 (2015) 345–362.

[21]Y. Pomeau, The transition to turbulence in parallel flow: a personal view, C. R. Mécanique 343 (2015) 210–218.

[22]P. Manneville, Dissipative structures and weak turbulence,Academic Press, Boston 1990.

[23]B. Murray, Mathematical biology, Springer-Verlag, 1993.

[24]D. Barkley, Simplifying the complexity of pipe flow, Phys. Rev. E 84 (2011) 016309.

[25]D. Barkley, Theoretical perspective on the route to turbulence in a pipe, J. Fluid Mech. 803 (2016) P1.

[26]P. Manneville, Turbulent patterns in wall-bounded flows: a Turing instability?, Eur. Phys. Lett. 98 (2012) 64001.

[27]M. Lagha, P. Manneville, Modeling of plane Couette flow: I.large scale flow around turbulent spots, Phys. Fluids 19 (2007)095105.