A new spallation mechanism of thermal barrier coatings on aero-engine turbine blades

Bo Yun, Christopher M. Hrvey, Rchel C. Thomson, Gry W. Critchlow, Simon Wng,*

aDepartment of Aeronautical and Automotive Engineering, Loughborough University, Loughborough, Leicestershire LE11 3TU, UK

bDepartment of Materials Engineering, Loughborough University, Loughborough, Leicestershire LE11 3TU, UK

cSchool of Mechanical and Equipment Engineering, Hebei University of Engineering, Handan 056038, China

Thermal barrier coatings (TBCs) can protect the engine components from high and prolonged heat loads, improve the durability and the engine energy efficiency [1, 2]. In the layered TBC system, an yttria stablized zirconia (YSZ) ceramic top coat is bonded on the metallic substrate by either an overlay or a diffusion bond coat. During thermal exposure, a layer of thermally grown oxide (TGO) is generated at the interface between the top coat and the bond coat.

TBCs can degrade and spall off from the alloy substrate at elevated temperatures or room temperature, then the exposed substrate will be oxidized and melted [3, 4]. The mechanisms of this spontaneous spallation failure are very complex and have stimulated considerable research studies with various considerations including sintering [5], oxidation [6], interface adhesion degradation [7], thermal stress due to the mismatch in coefficient of thermal expansion between the coating and the substrate [8], creep [9], and interface undulation geometry [4]. In the previous experiments, such as indentation test [10, 11], bending and buckling test [12, 13], scratch test [14] and push-out test [15],coupon samples were out of the blade shape; for the samples that cut from the blade, minor flaws could appear during preparation. The stress and strain fields in coupon samples may then be different from those in the intact blades. Therefore, the entire blades were tested in the present study. Specially, the top coat was coated by the electron-beam physical vapour deposition technique, and bonded by a/′ Pt-diffused bond coat which exhibits negligible rumpling due to the high creep resistance in heating-cooling cycles [16].

Extensive analytical and numerical studies have been carried out in last few decades for the spallation behaviour of TBC.Most studies are based on buckling driven delamination [4, 6,10-13, 17-19]. However, the buckling driven approach is insufficient to reveal the essential mechanics as discussed in the work[20, 21]. Wang, Harvey et al. [22, 23] recently developed a mechanical model, which hypothesized that pockets of energy concentration (PECs) resulted from pockets of interfaces stresses,and would be the driving energy for constant room temperature spallation failure. The aim of the current study is to apply the mechanical model in the work [22, 23] to study the spallation of TBCs, and compare the analytical predictions with experimental measurements.

It is believed that an introduction to the mechanical model by Wang, Harvey et al. [22, 23] is helpful to understand the present work.

Figure 1 sketches a circular separation blister of TBC with radiusRBand thicknessh. The subscript B represents the edge of the blister.

Fig. 1. A circular separation blister of TBC.

The blister grows when the driving force at the crack tip, i.e.,energy release rate (ERR) overcomes the fracture toughness. Different fracture partition theories lead to different mode mixity[24, 25]. The following derivations are based on the classical plate partition theory [24, 26, 27]. Using the linear fracture criterion, the blister energy at growth is

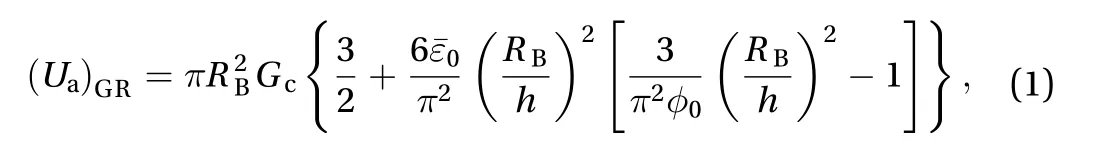
After nucleation, the blister grows slowly until the radius reaches the characteristic buckling length. Then, unstable growth starts at

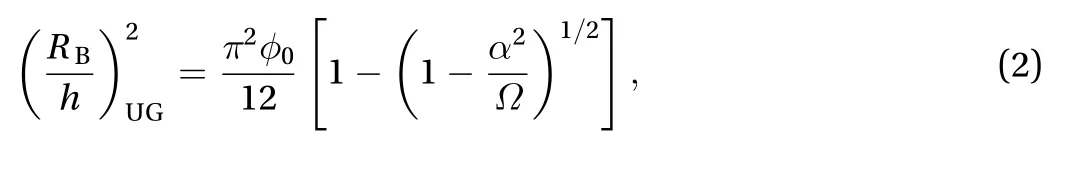
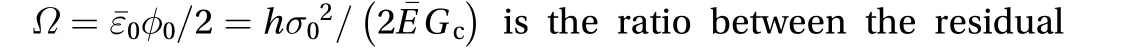
It is worth noting that the mentioned characteristic buckling is different from the bifurcation type buckling. In the conventional approach for buckling-driven delamination, the amplitudeAof the blister is zero at the instant of the buckling. However, the amplitudeAof the blister hereby is with a finite value. Hence, it is expected that the non-bifurcation type buckling occurs well before the bifurcation type buckling.

The violent unstable growth rapidly enlarges the size of the blister, and the blister energy will increase to a maximum value as suggested by Eq. (1). If the PECs are insufficient to supply the blister to arrive the maximum value, then the blister will stop growing. After the maximum value, the blister energy will decrease and transform into the kinetic energy. If the blister energy becomes zero and the kinetic energy of the blister due to the fast-unstable growth is large enough to break the blister edges,then the blister will spall off from the substrate. The spallation radius is calculated as

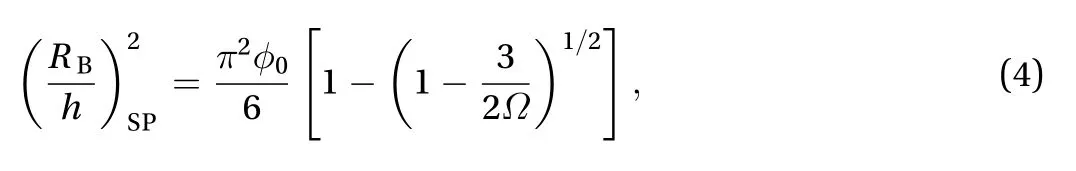
with SP denoting spallation. From Eq. (4), it is seen thathas to be larger than 3/2 for spallation to occur. When, Eq.(6) becomes

The blister amplitudeAis given in Eq. (6) below.

It is worth noting that only the blister radiusRBwas measured whilst the amplitudeA(out-of-plane displacement) was not measured in the present work since only one digital camera was used in the experiment.

The above derivations can be equally applied for either classical plate partition theory [24, 26, 27] or first-order shear-deformable plate partition theory [26, 27] or 2D elasticity plate partition theory [25, 28, 29]. However, the interface fracture toughnessGcneeds to be taken as,andrespectively for the three partition theories, whereis the critical mode I fracture toughness and.

The task now is to compare the blister radius between the analytical predictions and experimental measurements. First,the experimental method and the coating blister development is described as follows.

The specimen is the first-stage blade from a high-pressure turbine. It includes a single crystal CMSX-4 Ni-based superalloy substrate, and a Pt-diffusion bond coat. The α-alumina dominated oxides are generated at the interface between the bond coat and top coat during heating. The YSZ top coat has an average Young’s modulus of 30–40 GPa [30, 31]. The TGO’s Young’s modulus is around 380–400 GPa [17], and its thickness is 2–5 μm[12, 17, 31]. From the SEM observation of the spalled pieces in the present study, it is confirmed that spallation occurred at the interface between the TGO and the bond coat. Moreover, the thickness of the top coat and the TGO were found to be 138 μm and 5 μm respectively. For the present preliminary study, an equivalent Young’s modulus for the combined TBC and TGO thin layer is calculated by equating the effective in-plane stiffness in the radial direction, i.e.,. Takingand400 GPa gives the value of the equivalent Young’s modulus as. The Poisson's ratio is assumed to be 0.22. The compressive residual stress was generated during cooling, and the typical thermal expansion mismatch between the top coat and the Ni-substrate is 4 ppm·°C-1.

There were seven heating-cooling cycles (total 220 hours) in the experiments. The furnace was pre-heated at temperature of 1135°C, in which the specimen was isothermally oxidized. In the first thermal cycle, the heating duration was 100 hours, after which the specimen was cooled down to the room temperature under the laboratory condition in approximate 45 mins, and then it was kept for 195 mins at room temperature for failure observation, and no spallation failure occurred, hence about 0.05 kg·m-2water was gently sprayed by a sprayer on the convex surface of the blade. The specimen was observed for subsequent four hours at room temperature and no spallation occurrence. In the second thermal cycle, the heating duration was changed to be 20 hours. Again, after four hours when the specimen was moved out of the furnace, water was gently sprayed by a sprayer on the convex surface, and the specimen was kept for additional four days. No spallation occurrence. In the subsequent five heating-cooling cycles, the same procedure as the second thermal cycle was conducted, except that water was not sprayed any more. In the seventh thermal cycle, the specimen convex surface spalled shortly after the surface temperature had reached the room temperature.

The convex surface of the specimen maintained well in the first six thermal cycles, although being water sprayed in the first two cycles, which is in agreement with the work in Ref. [32]. The studies [33, 34] also show that water vapour in high volume percentage has largely no effect on the lifetime of the electron-beam physical vapour deposition technique (EB-PVD) TBCs with Ptdiffusion (/’) aluminide bond coat for various cycles with different oxidation duration. Therefore, a typical value of the mode-I interfacial fracture toughness is taken as 8.4 J∙m-2at the interface between the TGO and bond coat [12] and the fracture toughness ratiois taken to be 5 [35].

A digital camera was placed to the region near the convex surface, which is close to the trailing edge. Recording started once the specimen was moved out of the furnace. Note that the blister appeared and spalled at room temperature as described below, and hence the black body radiation effect is negligible and not considered in the present study. Figure 2 shows a sequence of optical and processed images for a blister development including nucleation, stable growth and unstable growth,brunching, and spallation on the convex surface. The stages of blister development are described according to radius growth rate.

The images of Fig. 2(b)-2(h) show the spallation failure process, in which the colour values were subtracted by the underlying colour of the reference image Fig. 2(a) [36]. It is seen that the blister appeared on the convex surface close to the blade trailing edge, which can be considered as a planar region. Although the compound subtract image-processing technique cannot capture the blister nucleation stage, there is a small spot in Fig. 2(b)observed, which is just discernible (circled in red) and can be regarded as the blister nucleation. It is seen that the size of this spot is much smaller than the buckling radius of 2.15 mm that is usually assumed in the conventional buckling approach from Eq. (3) with=1.22 (see Table 1 as follows). Although Eq. (6)shows that the height of the blister at this moment is very small,it is obviously not zero as usually assumed in the conventional buckling approach. For nucleation, the PECs need to provide the blister energyas given in Eq. (1). After nucleation, the blister grew steadily to the radius about 1.1 mm as shown in Fig. 2(c). The steady growth took about 1 s. It is worth noting that the nucleation and steady growth are driven by PECs.After the steady stage, an unstable growth occurred, and the blister abruptly grew in the shape shown in Fig. 2(d) within 0.033 s. This unstable growth is driven by both PECs and buckling. Although the blister is not a standard circular blister in Fig. 2(d), it is seen the right-half circle in Fig. 2(d) was developed from the circular blister in Fig. 2(c) and the radius was measured to be 2.5 mm.

Images (e) to (g) in Fig. 2 show the further unstable growth of the blister, which was still driven by PECs and buckling. The radius of the right-half circle of the blister in Fig. 2(e) was 2.8 mm.After 0.033 s, the blister branched as shown in image Fig. 2(f);however, the right-half blister remained circular with radius about 2.8 mm. Following that, the blister continued its unstable growth both in the branching directions and the right-half circular direction. The right-half circle radius in Fig. 2(g) was measured as 3.1 mm. Ridge cracks were also observed in Fig. 2(g).After about 1 s, both the blister and ridge cracks extended again and the radius of the right-half circle was measured as 3.3 mm.12 s after image Fig. 2(h), the branches extended very rapidly and detached from the substrate. The blister radius just prior to this was still 3.3 mm, and is regarded as the spallation radius.

Analytical predictions and experimental results from previous observations are compared as follows. Based on the material properties,are calculated:,, and, with CP, SP and 2D representing classical plate partition theory, first-order shear-deformable plate partition theory, and 2D elasticity plate partition theory, respectively. It is seen that all the three values are larger thanrequired by Eq.(2) and 1.5 required by Eq. (4). Therefore, the blister radii for the initiation of unstable growth can be predicted by Eqs. (2) and(3), and for the spallation can be predicted by Eqs. (4) and (5), as recorded in Table 1.

It is seen that the radius for the initiation of the unstable growth from experimental observation is very close to the analyt-ical prediction when taking=0.625 and is far smaller than 2.15 mm usually that is assumed in the conventional buckling approach from Eq. (3) with=1.22. The predictions for the spallation radius are also very close to the experimental result from all the three partition theories. Since, the Eq. (3) gives good approximation to Eq. (2), also, the Eq. (5) gives good approximation to Eq. (4), as seen in Table 1. This experimental observation clearly confirms the new spallation failure mechanism of thin layer materials which is hypothesized in the latest work [22, 23] for the study of thin film spallation. That is,the spallation of coating blister is driven by PECs and buckling.

In conclusion, spallation of EB-PVD TBCs with Pt-diffusion aluminide bond coat in aero-engine turbine blades can occur at constant room temperature after cooling down from the elevated temperature. The experimental measurements for the blister radius are compared with the analytical predictions from the PEC mechanical models [22, 23], specifically on the blister unstable growth and spallation. When the buckling parameterαis taken to be 0.652 representing a simple support blister edge condition, there is an excellent agreement between the measured and predicted unstable growth radius. Also, there is an excellent agreement between the measured and predicted spallation radius. Moreover, the nucleation radius is much smaller than the traditional buckling radius assumed in the conventional approach. The experimental work clearly demonstrates that the spallation of EB-PVD TBCs is driven by PEC – a new spallation failure mechanism.

Fig. 2. Sequence of optical and processed images showing the nucleation (b), stable growth (b-c) and unstable growth (c-g), branching (e-f)and spallation (h) of a blister on the EB-PVD TBC convex surface.

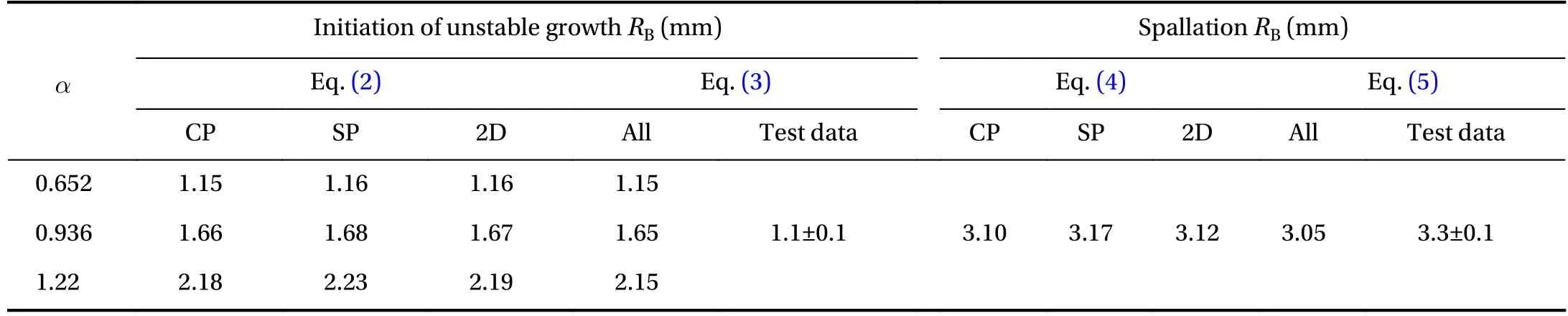
Table 1 Blister radius comparison for intitiaton of unstable growth and spallation.

[1]N.P. Padture, M. Gell, E.H. Jordan, Thermal barrier coatings for gas-turbine engine applications, Science. 296 (2002) 280–284.

[2]D.R. Clarke, M. Oechsner, N.P. Padture, Thermal-barrier coat-ings for more efficient gas-turbine engines, MRS Bull. 37 (2012)891–898.

[3]A.G. Evans, D.R. Clarke, C.G. Levi, The influence of oxides on the performance of advanced gas turbines, J. Eur. Ceram. Soc.28 (2008) 1405–1419.

[4]A.G. Evans, D.R. Mumm, J.W. Hutchinson, et al., Mechanisms controlling the durability of thermal barrier coatings, Prog. Mater. Sci. 46 (2001) 505–553.

[5]X. Zhao, X. Wang, P. Xiao, Sintering and failure behaviour of EB-PVD thermal barrier coating after isothermal treatment,Surf. Coatings Technol. 200 (2006) 5946–5955.

[6]L. Rémy, C. Guerre, I. Rouzou, et al., Assessment of TBC Oxidation-Induced Degradation Using Compression Tests, Oxid.Met. 81 (2014) 3–15.

[7]P.-Y. Théry, M. Poulain, M. Dupeux, et al., Spallation of two thermal barrier coating systems: experimental study of adhesion and energetic approach to lifetime during cyclic oxidation,J. Mater. Sci. 44 (2009) 1726–1733.

[8]M. Martena, D. Botto, P. Fino, et al., Modelling of TBC system failure: Stress distribution as a function of TGO thickness and thermal expansion mismatch, Eng. Fail. Anal. 13 (2006)409–426.

[9]D.S. Balint, S.-S. Kim, Y.-F. Liu, et al., Anisotropic TGO rumpling in EB-PVD thermal barrier coatings under in-phase thermomechanical loading, Acta Mater. 59 (2011) 2544–2555.

[10]Y. Liu, V. Vidal, S. Le Roux, et al., Influence of isothermal and cyclic oxidation on the apparent interfacial toughness in thermal barrier coating systems, J. Eur. Ceram. Soc. 35 (2015)4269–4275.

[11]H. Bhatnagar, S. Ghosh, M.E. Walter, Parametric studies of failure mechanisms in elastic EB-PVD thermal barrier coatings using FEM, Int. J. Solids Struct. 43 (2006) 4384–4406.

[12]X. Zhao, J. Liu, D.S. Rickerby, et al., Evolution of interfacial toughness of a thermal barrier system with a Pt-diffused/′bond coat, Acta Mater. 59 (2011) 6401–6411.

[13]J.-R. Vaunois, M. Poulain, P. Kanouté, et al., Development of bending tests for near shear mode interfacial toughness measurement of EB-PVD thermal barrier coatings, Eng. Fract. Mech.171 (2017) 110–134.

[14]L. He, Z. Xu, X. Cao, et al., Adhesive strength of new thermal barrier coatings of rare earth zirconates, Vacuum. 83 (2009)1388–1392.

[15]M., Delamination toughness of electron beam physical vapor deposition (EB-PVD) Y2O3-ZrO2 thermal barrier coatings by the pushout method: Effect of thermal cycling temperature, J.Mater. Res. 23 (2008) 2382–2392.

[16]D.S. Rickerby, S.R. Bell, R. Wing, Article including thermal barrier coated superalloy substrate, 1999.

[17]J.-S. Wang, A.G. Evans, Measurement and analysis of buckling and buckle propagation in compressed oxide layers on superalloy substrates, Acta Mater. 46 (1998) 4993–5005.

[18]S.R. Choi, J.W. Hutchinson, A.G. Evans, Delamination of multilayer thermal barrier coatings, Mech. Mater. 31 (1999)431–447.

[19]J.-W. Guo, L. Yang, Y.-C. Zhou, et al., Reliability assessment on interfacial failure of thermal barrier coatings, Acta Mech. Sin.32 (2016) 915–924.

[20]V.K. Tolpygo, D.R. Clarke, Spalling failure of α-alumina films grown by oxidation: I. Dependence on cooling rate and metal thickness, Mater. Sci. Eng. A. 278 (2000) 142–150.

[21]V.K. Tolpygo, D.R. Clarke, Spalling failure of α-alumina films grown by oxidation. II. Decohesion nucleation and growth, Mater. Sci. Eng. A. 278 (2000) 151–161.

[22]C.M. Harvey, B. Wang, S. Wang, Spallation of thin films driven by pockets of energy concentration, Theor. Appl. Fract. Mech.92 (2017) 1–12.

[23]S. Wang, C.M. Harvey, B. Wang, Room temperature spallation of α-alumina films grown by oxidation, Eng. Fract. Mech. 178(2017) 401–415.

[24]S. Wang, C. Harvey, A theory of one-dimensional fracture,Compos. Struct. 94 (2012) 758–767.

[25]J.D. Wood, C.M. Harvey, S. Wang, Partition of mixed-mode fractures in 2D elastic orthotropic laminated beams under general loading, Compos. Struct. 149 (2016) 239–246.

[26]C.M. Harvey, S. Wang, Mixed-mode partition theories for onedimensional delamination in laminated composite beams, Eng.Fract. Mech. 96 (2012) 737–759.

[27]S. Wang, C.M. Harvey, Mixed mode partition theories for one dimensional fracture, Eng. Fract. Mech. 79 (2012) 329–352.

[28]J.W. Hutchinson, Z. Suo, Mixed Mode Cracking in Layered Materials, in: Adv. Appl. Mech., 1991: pp. 63–191.doi:10.1016/S0065-2156(08)70164-9.

[29]C.M. Harvey, J.D. Wood, S. Wang, et al., A novel method for the partition of mixed-mode fractures in 2D elastic laminated unidirectional composite beams, Compos. Struct. 116 (2014)589–594.

[30]E.P. Busso, Z.Q. Qian, M.P. Taylor, et al., The influence of bondcoat and topcoat mechanical properties on stress development in thermal barrier coating systems, Acta Mater. 57 (2009)2349–2361.

[31]D. Liu, C. Rinaldi, P.E.J. Flewitt, Effect of substrate curvature on the evolution of microstructure and residual stresses in EBPVDTBC, J. Eur. Ceram. Soc. 35 (2015) 2563–2575.

[32]M. Brossard, B. Bouchaud, G. Bonnet, et al., Early stages of high temperature cyclic oxidation of an electrodeposited ceria coating on nickel superalloys under water-drop tests, in: Oxid. Met.,2014: pp. 95–104. doi:10.1007/s11085-013-9426-7.

[33]K.A. Unocic, B.A. Pint, Effect of water vapor on thermally grown alumina scales on bond coatings, Surf. Coatings Technol. 215(2013) 30–38.

[34]B.A. Pint, K.A. Unocic, J.A. Haynes, The Effect of Environment on TBC Lifetime, in: ASME Turbo Expo 2015 Turbine Tech.Conf. Expo., 2015: p. V006T21A013. doi:10.1115/GT2015-43762.

[35]N.A. Fleck, A.C.F. Cocks, S. Lampenscherf, Thermal shock resistance of air plasma sprayed thermal barrier coatings, J. Eur.Ceram. Soc. 34 (2014) 2687–2694.

[36]J.I. Greenberg, T.I. Kolb, C. Steele, et al., Adobe Premiere Pro Studio Techniques, Adobe Press, 2013.