Thermoelastic vibrations in a thin elliptic annulus plate with elastic supports

Vinod Vrghese, Tr Dhkte*, Llsingh Khls

aDepartment of Mathematics, Smt Sushilabai Rajkamalji Bharti Science College, Arni, Yavatmal, India

bDepartment of Mathematics, Mahatma Gandhi Science College, Armori, Gadchiroli, India

The thermoelastic vibration analysis is necessitated in many engineerings science applications such as design and computation of structures and mechanical devices, maintenance or predictions of breakdown. These reasons make the study of thermoelastic vibrations in structures and the control of their behaviour under dynamic loads an interesting study. There are a significant number of circumstances in which it is possible to diminish, but not to remove the dynamic forces that excite a system provoking a vibratory behaviour on it. Even loads produced by an earthquake or by wind are unpredictable variables that subject structures to variable dynamic loads. Hence, the displacements caused by dynamic loads, either in the form of thermal or pressure, need to be reduced. This thermoelastic analysis becomes relevant not only for the prediction of thermal displacements, and the related deformations and tensions, but also for their control. Therefore, some theoretical studies concerning the problems of various elastic structural vibrations using different methods have been testified so far. Compared to the cases of rectangular and circular plates, the transverse vibration characteristics of elliptical plates has far less been studied,due to the complexity of obtaining an analytic solution as well as the inadequacy of computational tools for finding numerical solutions. In this paper, we propose a theoretical problem of thermoelastic vibrations in a thin elliptic annulus plate with elastic supports that are used in a variety of engineering applications due to its suitable adaptability with experimental results.

A short history of the research investigations associated with the thermoelastic vibrations insights using various operational and approximate methods like the Ritz energy method,Galerkin’s method, finite element models and perturbation theory are reviewed that is used to solve the system. Several authors have studied the flexural vibration problems in elliptic structures since the pioneering works of Mathieu on the vibration of elliptic membranes in the nineteenth century. For example,Chen et al. [1] introduced three displacement functions to decompose three displacement components so that the three-dimensional equations of motion of a transversely isotropic body are uncoupled. Further expanding these functions in terms of orthogonal series, the equations of free vibration problem of a transversely isotropic cylindrical shell with ends simply supported are simplified. Sato [2, 3] obtained solutions for composite elliptical membrane consisting of confocal elliptical parts under certain conditions during free as well as forced vibration analysis. Hutchinson and El-Azhari [4] use exact series solutions to the exact governing equations and present highly accurate resonance frequencies of stress-free cylinders by the linear three-dimensional theory of elasticity. Yii and Buchanan [5] use the finite element method to study the effect of Poisson’s ratio on the resonance frequencies of free finite hollow cylinders. El-Raheb[6] analyses inhomogeneous hollow cylinders with normal components of time-dependent displacement and stress specified over different parts of the same surface. Gaunaurd and Everstine [7] analyse a hollow elastic cylinder encased in a tube and subject to uniform static compression at the ends. Hasheminejad and Mirzaei [8] analyse a simply supported elastic circular cylinder of finite length with an eccentrically located inner circular cavity, zero stress on the curved surfaces, and shear diaphragm end conditions. Haider [9] investigated the nonlinear forced vibrations of a thermally loaded annular plate with clamped-clamped immovable boundary conditions in the presence of a three-to-one internal resonance between the first and second axisymmetric modes. Kukla [10] investigated the thermally induced vibration of a homogeneous thin circular plate and obtained the solution by using the Green’s function method. Recently an excellent article by Yao et al. [11] provides a detailed analysis of free vibration of the clamped elliptical plate,when temperature and stress fields are coupled, with the utilisation of Galerkin’s method. Youssef [12] investigated the generalised thermoelastic vibration of a bounded nano-beam resonator induced by ramp type of heating using Laplace transforms. Bera[13] developed an approximate theory which can seem quite appropriate for handling issues of plates, significantly in elliptical coordinates system, both for simple and arbitrary shapes. The solution of problems with bending of a plate was adopted by the rough arrange of the outline of the deflected surface of the plate being physically compatible with the kind of fastening at the boundary, the character of the surface loads, and also the geometrical form of the plate. Hasheminejad et al. [14] formulated eigenfunction expansion in terms of transcendental Mathieu and modified Mathieu functions employed to present the first known exact time-domain series solution for transverse vibrations of a uniform elastic membrane of elliptical shape under arbitrary loading and initial conditions. Ebenezer and Ravichandran [15] analysed free vibrations of cylinders with free or fixed boundaries and forced vibrations of cylinders with specified non-uniform displacement or stress on the boundaries using three series solutions. Kukla [16] derived the Green’s function of the Helmholtz operator in an elliptical region and obtained a solution in the form of a double series of Mathieu functions. Very recently, Bhad et al. [17, 18] and Dhakate [19] determined the thermally induced transverse vibration of a uniform thin elliptical object using few new integral transform methods. Though, it has been proved that ample cases of thermoelastic vibration in solids have led to various technical problems in mechanical applications in which heat produced is rapidly sought to be transferred or dissipated.In fact, the thermally induced strain due to cyclic changes in temperature within the flexible range of plate produces a response to transverse vibration in objects. From the above reviews of previous literature indicates that there exist some notable analytical procedures that utilise various analytic, semi-analytic, or approximate numerical methods to investigate the vibrational characteristics. The thermally induced vibration problem in elliptical profile with various complicating effects has received no rigorous analytical or numerical solutions describing the thermoelastic response of solid or annular elliptical structures. The primary purpose of the current work is to take advantage of unified integral transform technique by use of Mathieu functions and modified Mathieu functions to fill this significant gap to obtain the exact solution.The presented analytical model is of both academic and technical interest primarily due to its inherent value as a canonical problem in structural thermodynamics and can serve as the benchmark for the evaluation of other solutions obtained by approximate computational techniques or asymptotic approaches.It can form an invaluable guide for design engineers in assessing the effects of changing the plate eccentricity and edge conditions for elliptical structural components in various physical and technological applications.

This study aims to determine the thermal bending stresses using the exact formal solution of the partial differential equation prevailing the transverse vibration in terms of Mathieu functions and modified Mathieu functions. During problem formulation, we have initially solved heat conduction equation using the integral operation method. Secondly, we shall study the thermoelastic symmetrical vibration with elastic supported boundaries conditions using the theory of integral transform. Finally,the analytical solution for the thermal stress components is obtained based on resultant bending moments per unit width. Results of four other cases corresponding to the constant temperature distribution and temperature prescribed to a point on the upper face of the disk have been briefly described. The results presented here will be more useful in engineering problems particularly in vibrational analysis and in determining the state of strain in elliptical disk constituting foundations for reactors,pressure vessels, furnaces, etc.

It is assumed that a thin elliptical annulus plate is occupying the spaceunder transient temperature state having internal heat source within it, while supports at the boundaries as non-rigid. The geometry of the elliptical annulus plate indicates that an elliptic-cylindrical coordinate systemis the most appropriate choices of the reference frame, which are related to the rectilin-ear coordinate systemby the relation,,. The curves= constant represent a family of confocal hyperbolas while the curvesξ= constant constitute a family of confocal ellipses. Both sets of curves intersect each other orthogonally at every point in space. Now, we assume that the boundary ofDis comprised of two confocal ellipses. The semi-major axis from inner long diameterto outer long diameter, whereas semi-minor axis moves from the inner short diameterto the outer short diameter. The length 2cis the distance between their common foci as shown in the geometrical configuration described in Fig. 1, which can be

The heat conduction equation and boundary conditions are given as

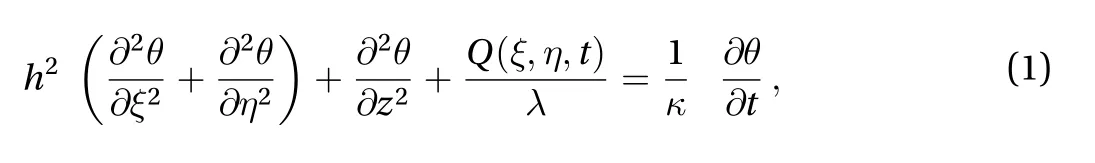
The heat generation term is assumed in the form

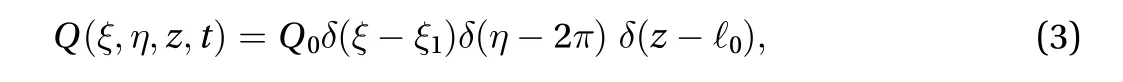
The temperature distribution in the elliptical plate is obtained as a solution of the Eq. (1) with the following initial and boundary conditions

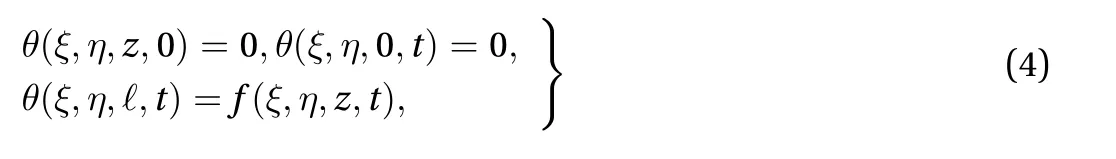
During the formulation we assume few postulates that (i) the thickness of the elliptical annulus plate is small compared to the other dimensions of the plate, (ii) strain is nil at the middle surface of the plate, (iii) transverse shear and normal strains are neglected during investigation, (iv) shear stress is small compared to other stress, influence of shear and rotary inertia is neglected, and (v) finally the temperature distribution depends upon variable position and time. The differential equation for the transverse displacement of an elliptical annulus plate with small amplitude, in elliptic-cylindrical coordinate system and with the restriction that the transverse displacement of a point on the middle plane can be considered in two parts: the quasistatic solution, in which inertia effects and damping are disregarded, satisfying the equation

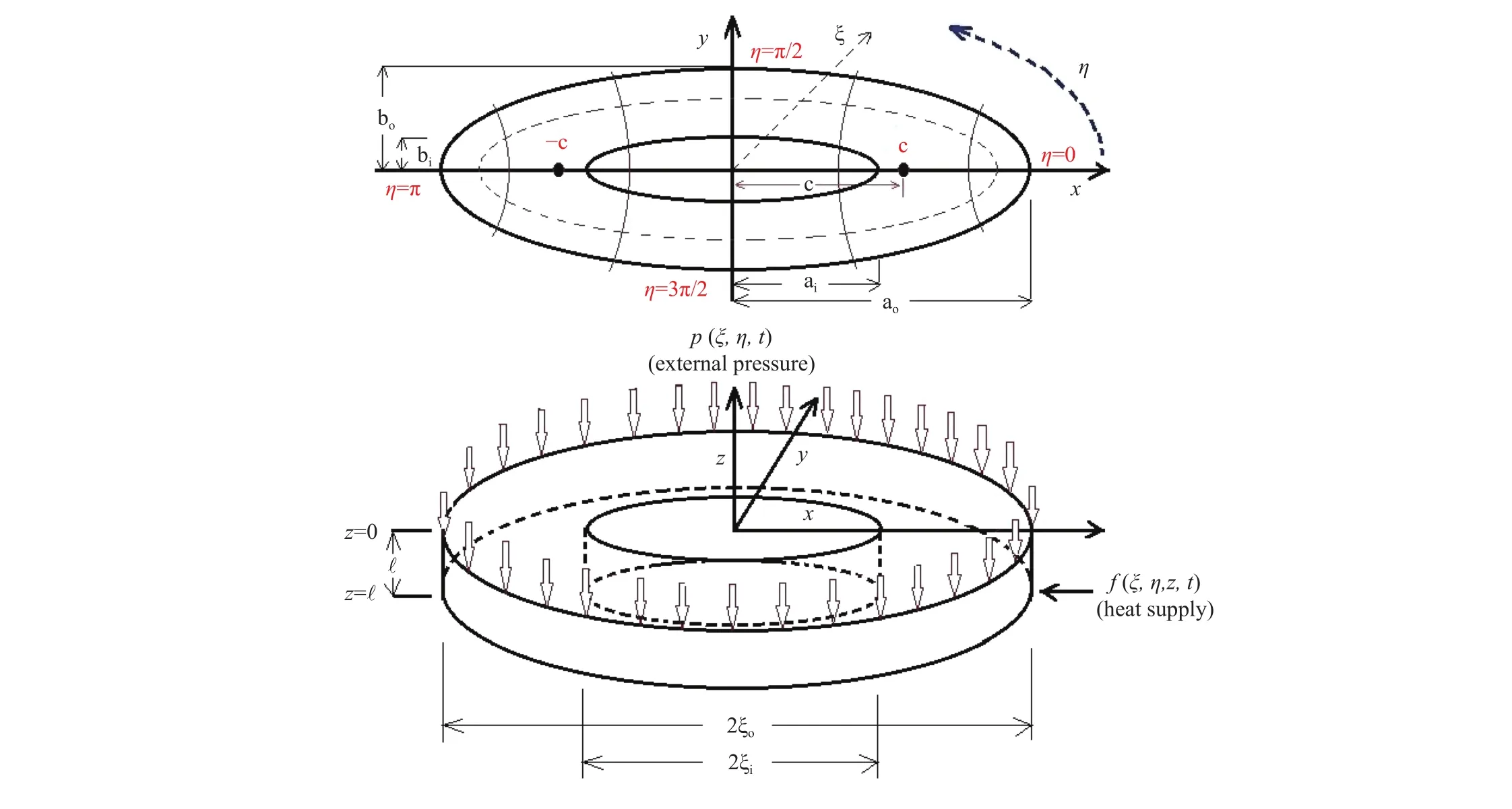
Fig. 1. Elliptic geometry of the problem

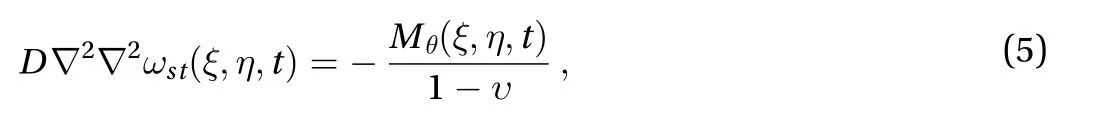
moreover, the dynamic solutionsatisfying the equation

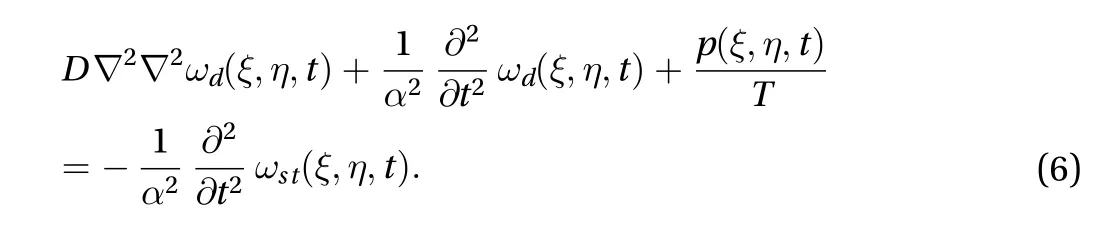
Now putting together both Eqs. (5) and (6), yields the complete solution as

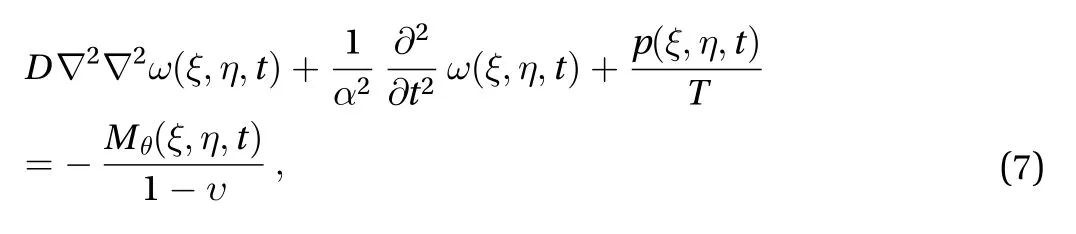
If we suppose that the boundaries of the thin annulus plate,submerged in a non-viscous medium, then the boundary conditions, expressed in mathematical forms, as

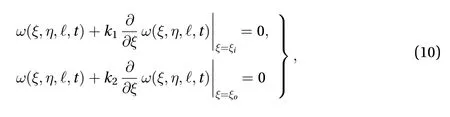
moreover, the initial conditions as

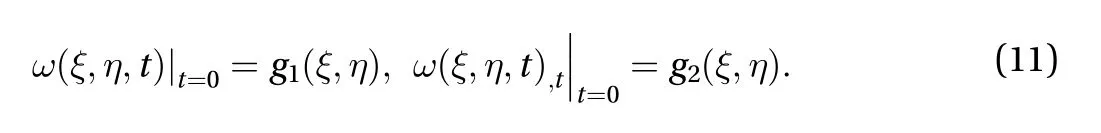
The maximum normal stresses acting on those sections are parallel toorplanes. Furthermore, the thermal stress components can be determined using small deflection and resultant moment as

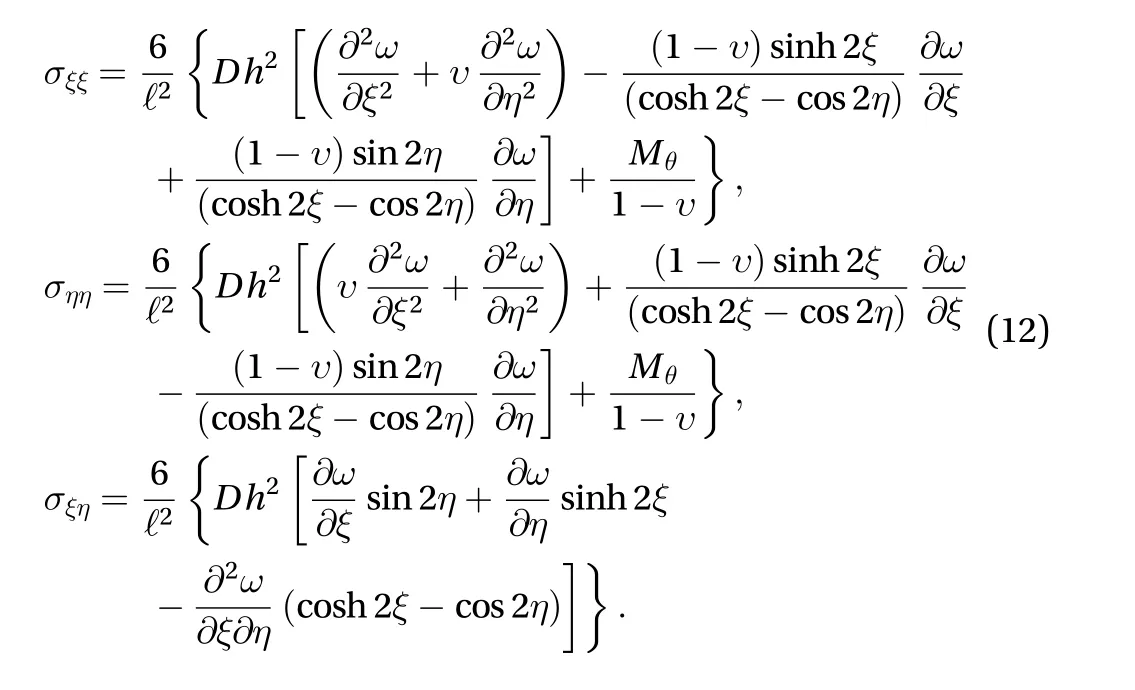
Equations (1)-(12) constitute the mathematical formulation of the problem under consideration.as

To solve fundamental differential Eq. (1), firstly we introduce the here a finite transform (refer Appendix) over the variables

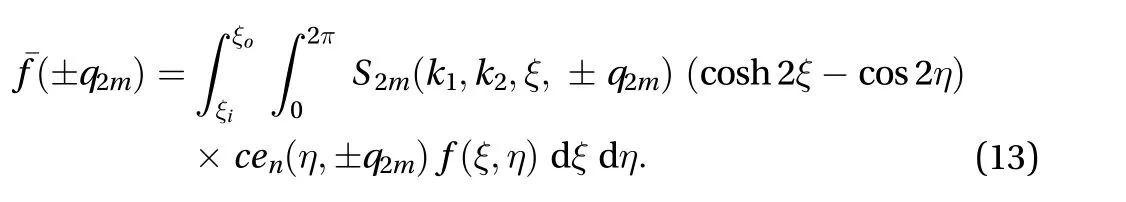
In this way, we may define the inversion theorem of Eq. (13)in the form

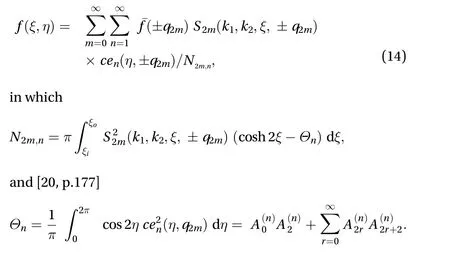
The notations of the Mathieu functions used in this paper follow those adopted by McLachlan [20]. So, the symbolsanddenote the Mathieu and modified Mathieu functions of ordernandmrespectively. The prime (′) attachedandrepresent theandderivatives respectively. The symbolsare the Fourier coefficients of the Mathieu functions. On applying an integral transform to the differential Eq. (13), and taking into account the boundary conditions (4), the differential Eq.(1) transformed into

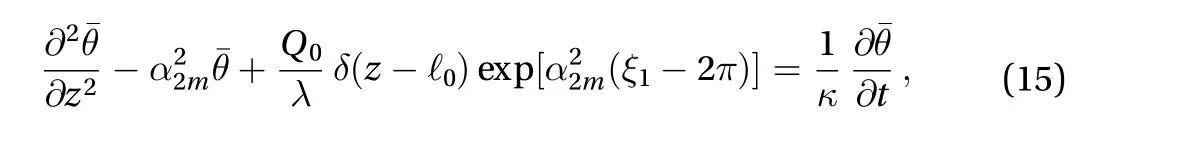
with initial and boundary conditions

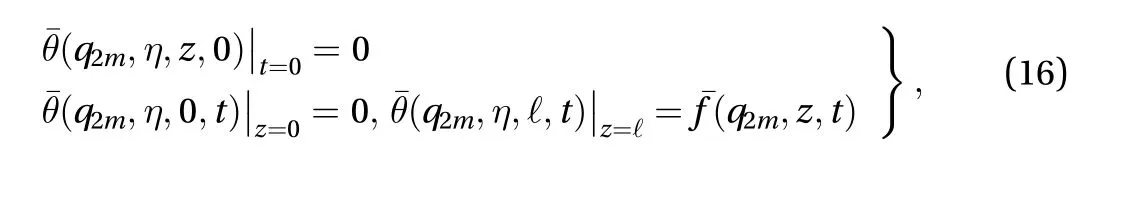
Applying Fourier sine transform to the Eq. (16), using the boundary conditions (16), one yield,

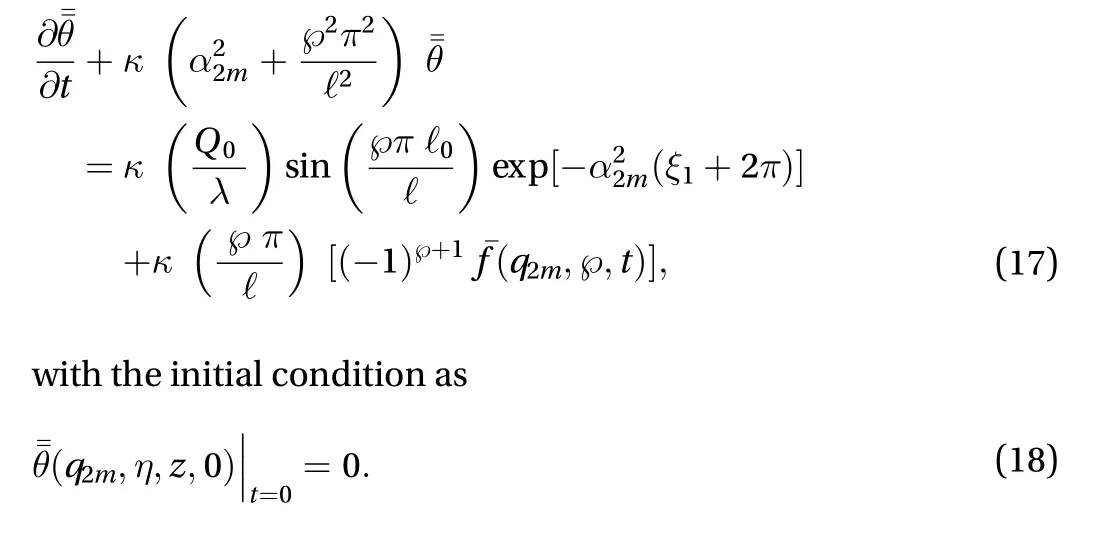
Applying Laplace transform to the Eq. (17), and taking into account the condition Eq. (18), the equation after mathematical simplification reduces to

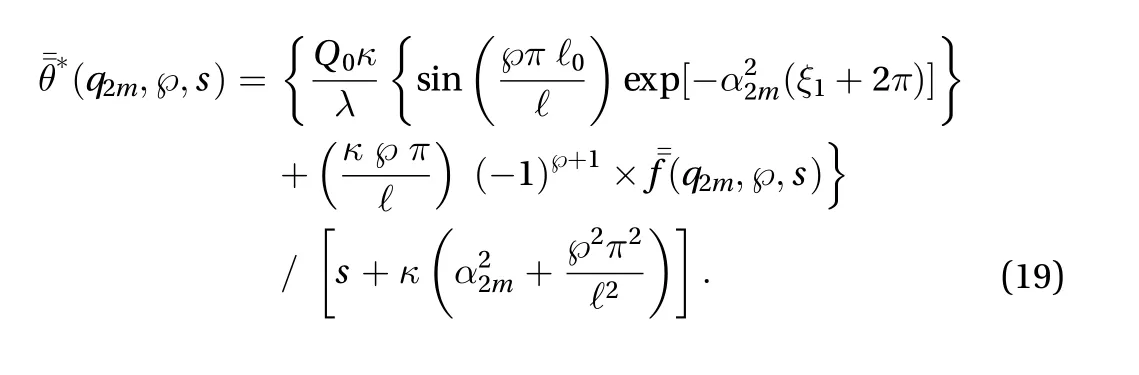
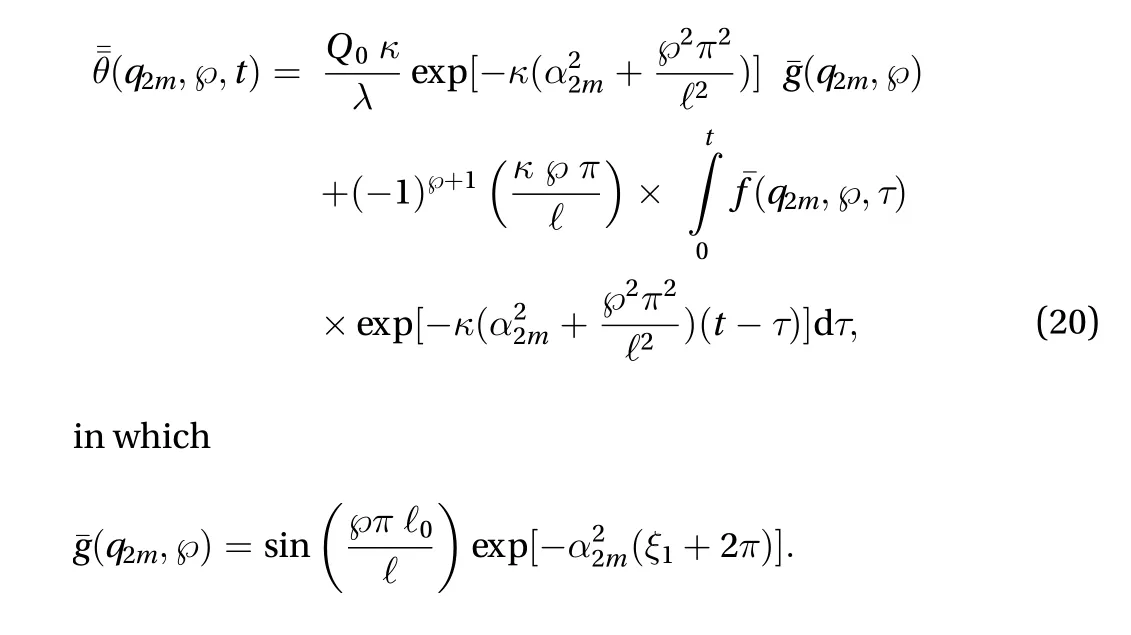
Applying inverse Laplace transform on Eq. (19), one obtains

Applying inversion theorem of the finite Fourier Sine transform on Eq. (20), one obtains,

Applying inversion theorem of the transformed rules defined by Eq. (14) on Eq. (21), the temperature is obtained as,

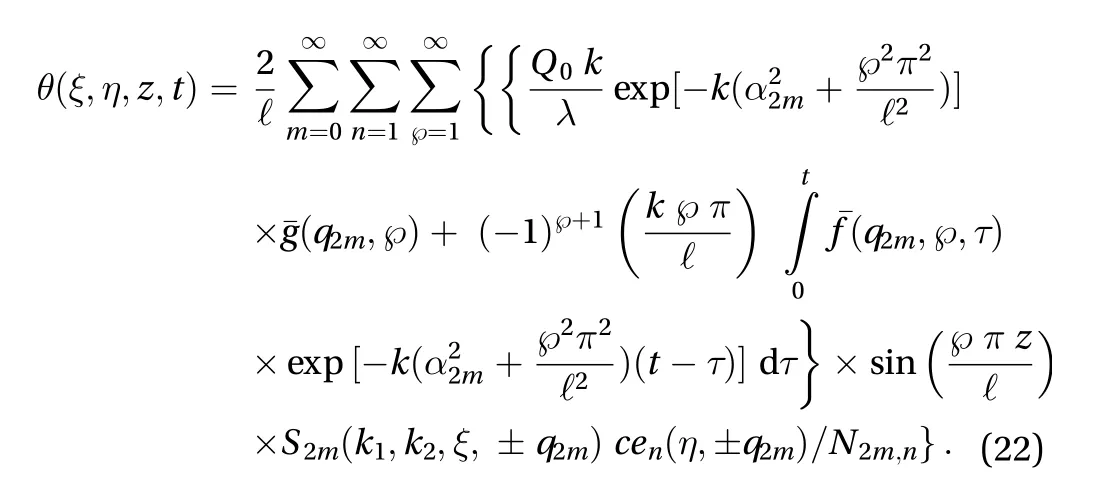
The function is given in Eq. (22) represents the temperature at every instant and at all the points of the elliptic annulus plate of finite height under conditions of radiation type on the surface.

Substituting the Eq. (22) in Eq. (8), the thermally induced resultant moment is obtained as

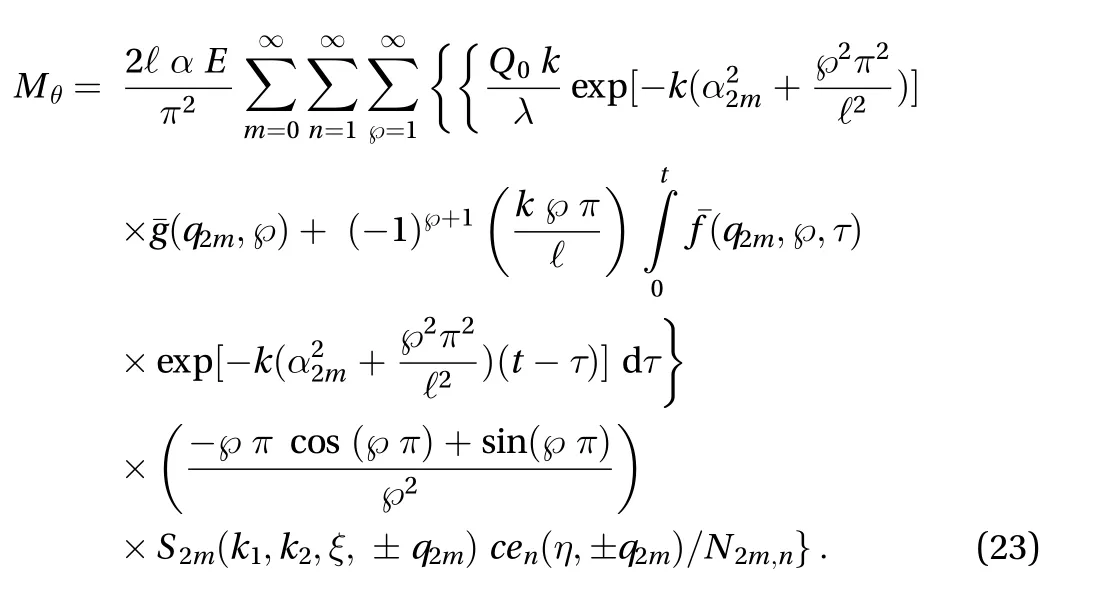
In order to solve fourth order differential Eq. (7), using another integral transformation (refer Appendix) of ordermandnover the variableξandηas

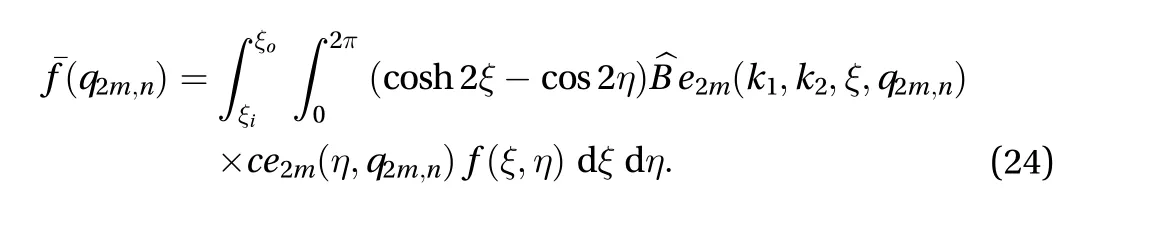
The inversion theorem of Eq. (24) is

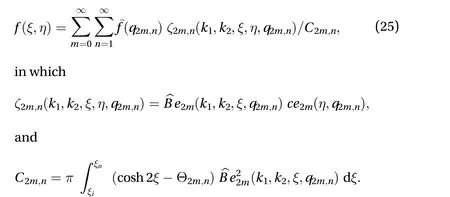
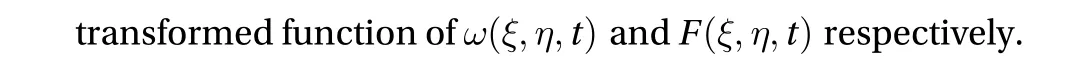
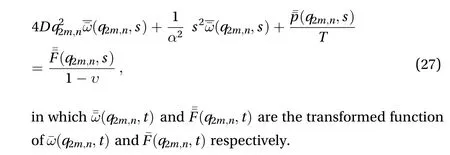
Using Laplace transform on Eq. (26), the differential equation is reduced to

Using the inverse Laplace theorem and the inverse theorem defined in Eq. (25), one obtains,

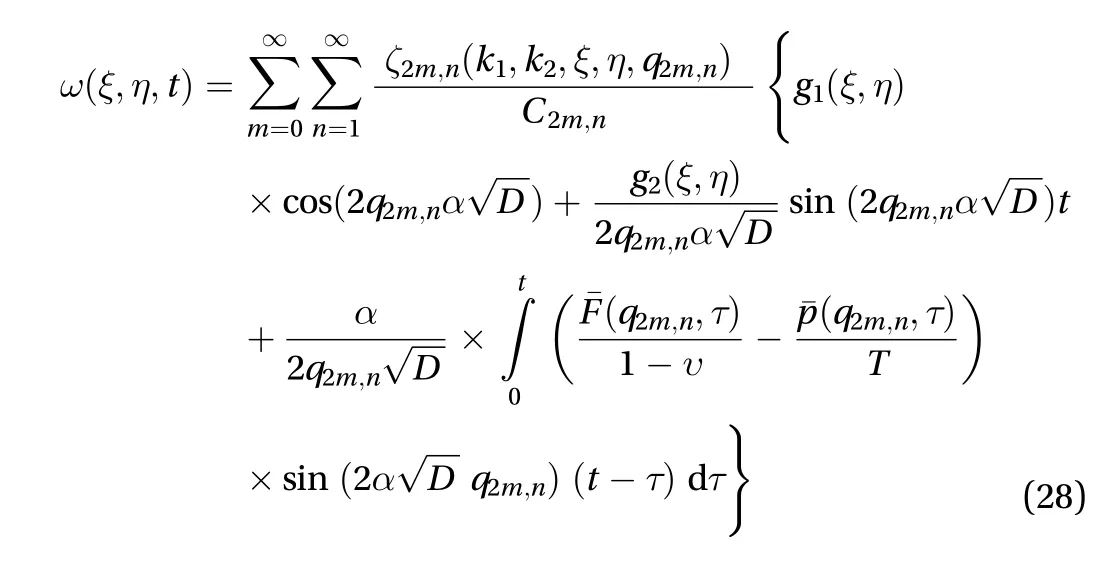
The resulting equation of stresses can be obtained by substituting Eqs. (23) and (28). The equations of stresses are rather lengthy, and the same has been omitted here for the sake of brevity but have been considered during graphical discussion using MATHEMATICA software.

When the elliptical annulus plate tends degenerates into a circular annulus plate with the thickness, internal radius, and outer radius, occupying the space, where,in such a way that,and[20] and takingindependent of. For that we take,

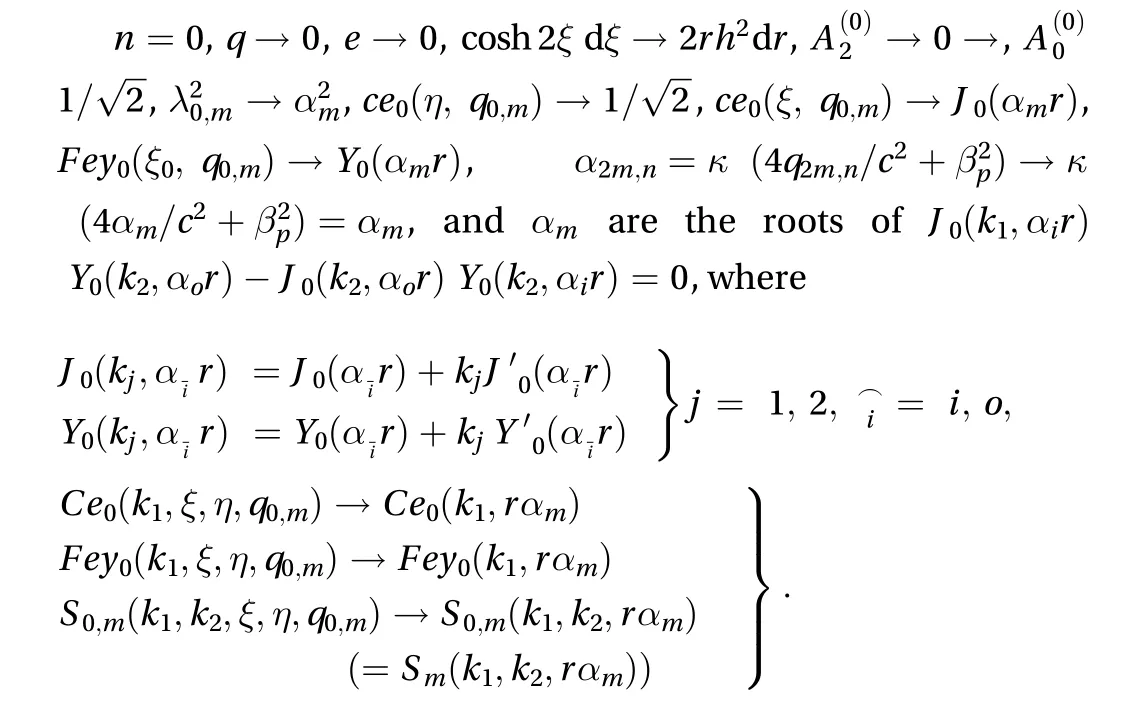
Equation (22) degenerates into temperature distribution in hollow circular disc

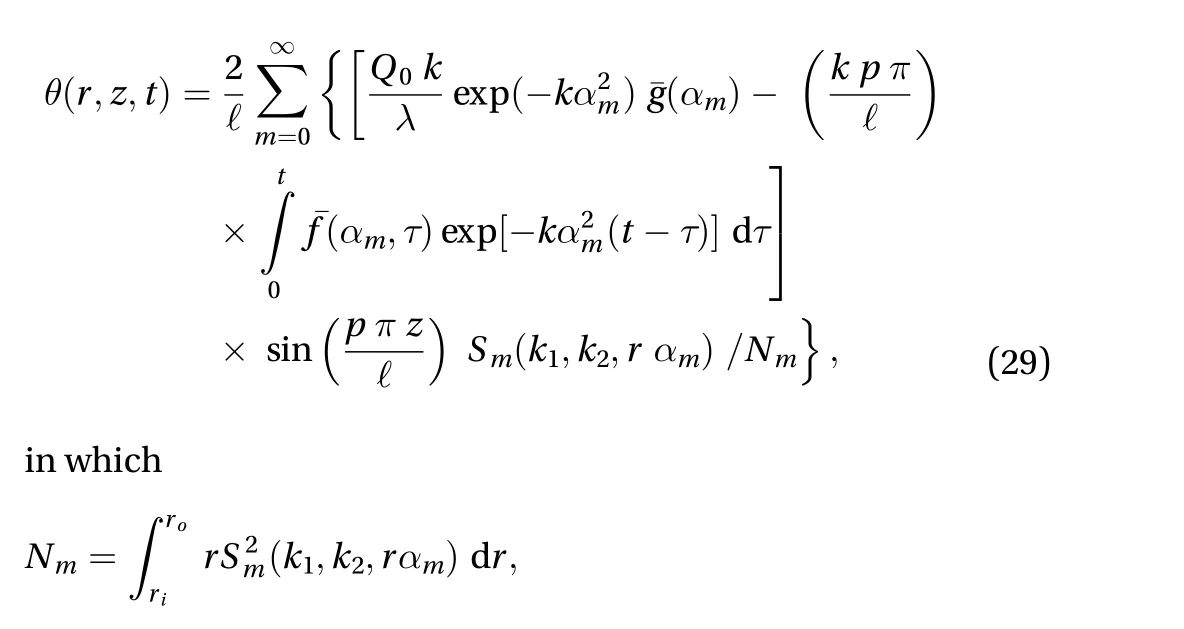
moreover, the kernel can be defined as

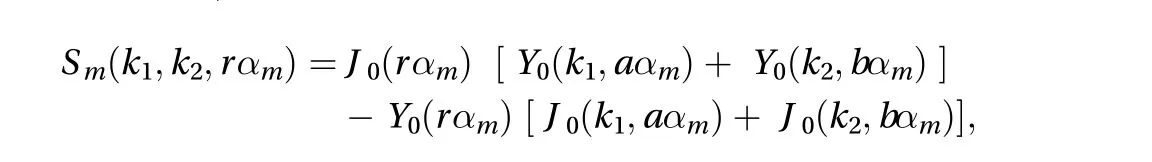
Suppose the elliptical annulus plate is subjected with a point impulsive sectional heat supply and applied pressure over the portionthat is varying with the time, that is to say

By substitution of this expression into Eqs. (22) and (28), we arrive at the results

By using Eqs. (31) and (32), we get the equations for the resultant moment and thermal stresses.

For the sake of simplicity of calculation, we introduce the following dimensionless values

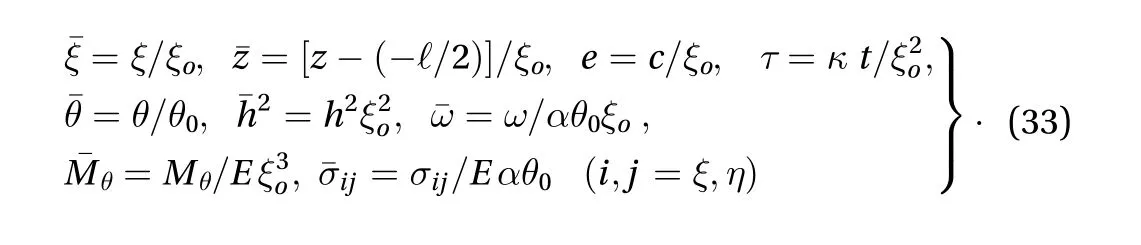
The mathematical computations have been carried out for Aluminum (pure) elliptic annulus plate with the thermo-mechanical properties are considered as modulus of elasticityE= 70 GPa, Poisson’s ratioυ= 0.35, thermal expansion coefficientα=23×10-6K-1, thermal diffusivityκ= 84.18×10-6m2∙s-1, densityϱ=2712 kg/m3and thermal conductivityλ= 204.2 W∙m-1∙K-1. The, 0.3987, 0.889, 1.5792, 2.4694, 3.5550, 4.8861,6.3467, 7.9993, 9.8696, 11.9523, 14.2322, 16.6792, 19.0234,21.2164, 23.6036, 25.0374, 27.7169, 29.2712, 31.0449 are the positive and real roots of the. Substituting the value of Eq. (33) in temperature Eq. (31), thermal deflection, thermal moment, and elements of stresses, we obtained the expressions for the temperature, deflection, resultant moment and thermal stresses respectively for our numerical calculation. The physical parameter as= 0.3 m,= 1 m,= 0.05 m, and reference temperatureas 150 °C. For numerical thermoelastic analysis, we have considered various values of time as, a fixed value). To examine the influence of heating on the plate, the numerical calculations were performed for all the variables, and numerical calculations are depicted in the following figures with the help of MATHEMATICA software. Plotted figures below illustrates the numerical results of temperature, deflection and stresses of an elliptic annulus plate subjected to a thicknessin which one face is at the zero temperature while the other face has prescribed temperature.

Figures 2–11 illustrates the numerical results of temperature distribution, thermal deflection and stresses on elliptic annulus plate due to the internal heat generation within the solid, under thermal boundary condition that is subjected to a known temperature at any instant timeτ. As shown in Fig. 2, the temperature increases as the time proceeds along the radial direction and is greatest at the other edge of the plate due to the combined energy of internal heat generation and known temperature. Figure 3 shows that the temperature distribution along the-direction for different values of time, which is maximum towards outer edge due to energised heat supply.

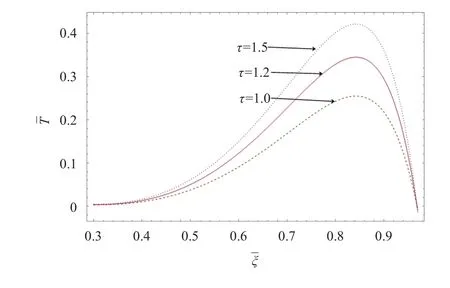
Fig. 2. Temperature distribution along radial direction for different values.

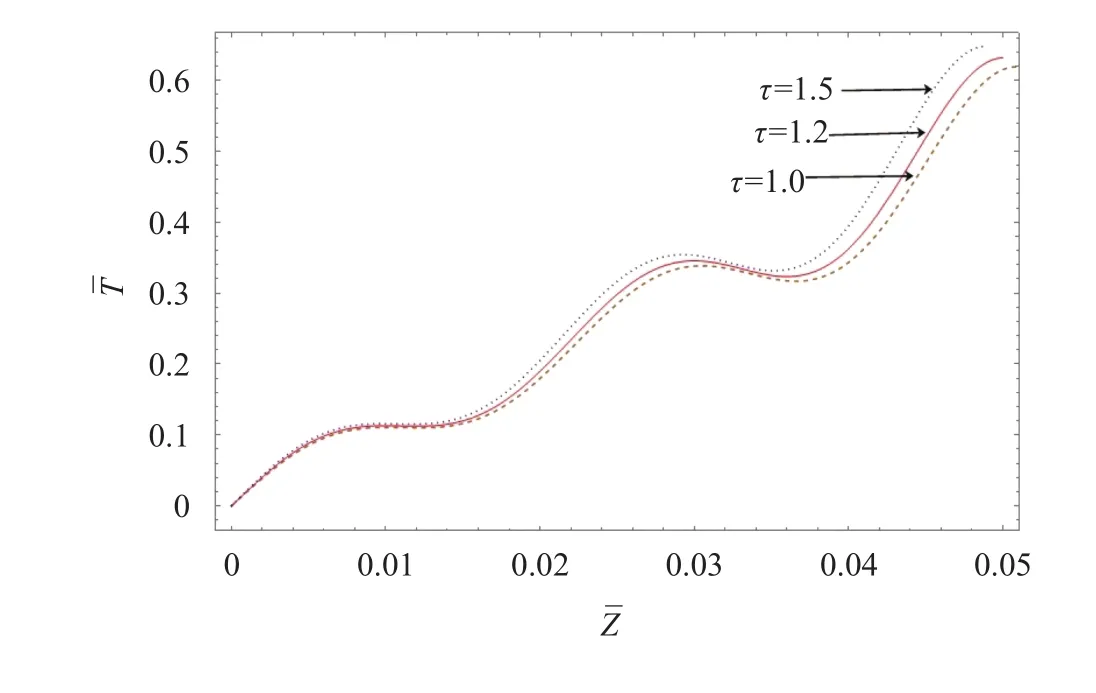
Fig. 3. Temperature distribution along- direction for different values.

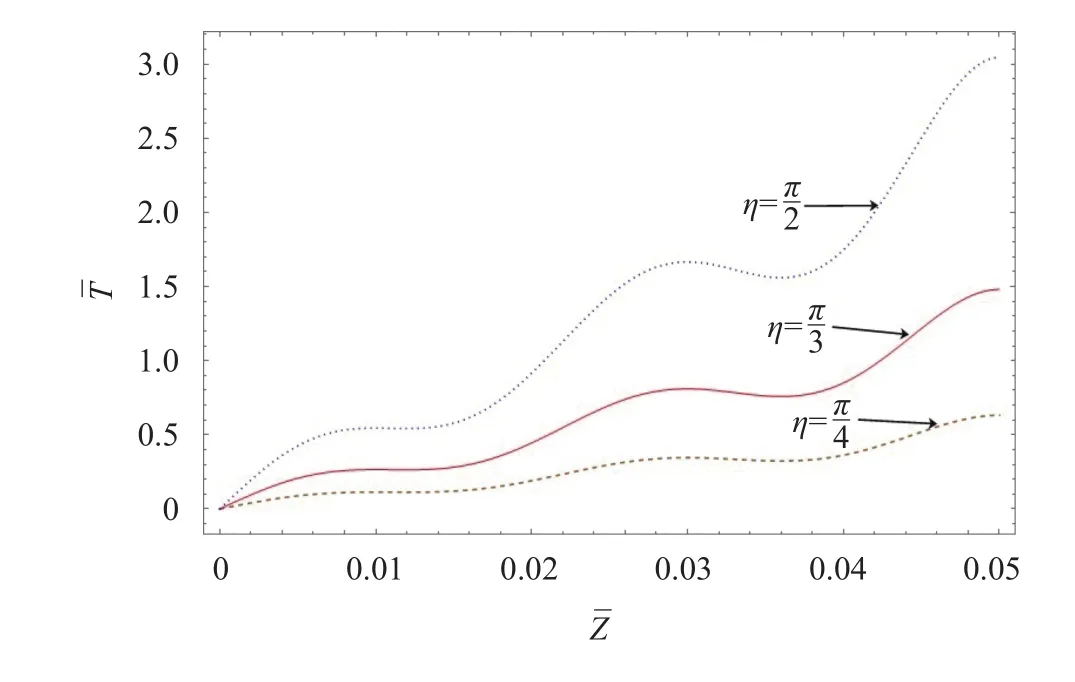
Fig. 4. Temperature distribution along- direction for different values.

Fig. 5. Thermal deflection along radial direction for different.

Figure 4 depicts that the temperature distribution along-direction for different values ofηattains maximum expansion at its outer core. There is an increment in the rate of heat propaga-tion with a thickness which leads to compressive force in the inner part and expands more on the outer surface whenever graph was plotted for temperature distributions, stress functions and deflection.

Figures 5 and 6 illustrate that the thermal deflection distribution over the plate with elastic supported edges. Figure 5 shows that the changes of thermal deflection along-direction for different time parameter. The deflection is highest at the other edge of the plate due to the combined effect of internal and external supplied energy. Figure 6 depicts that the thermal deflection along withfor different values ofattains a maximum at the outer edge and minimum at the inner edge of the disc satisfying boundary condition of first equation of (29).

Figure 7-9 shows the variation of thermal radial stress,tangential stressand shear stressalong the radial direction for different time parameter. From Fig. 7, the large compressive stress occurs at the inner edge while the tensile stress occurs at the outer edge which drops along the radial direction.From Fig. 8, it is observed that the maximum tensile stress occurs at outer core of the plate due to the combined energy of internal heat generation and external energy supply. From Fig. 9, It is clear that at the early stage, maximum stress occurs. It is almost zero in the interior to the plate, then attains minimum to-wards outer curve along the radial axis.

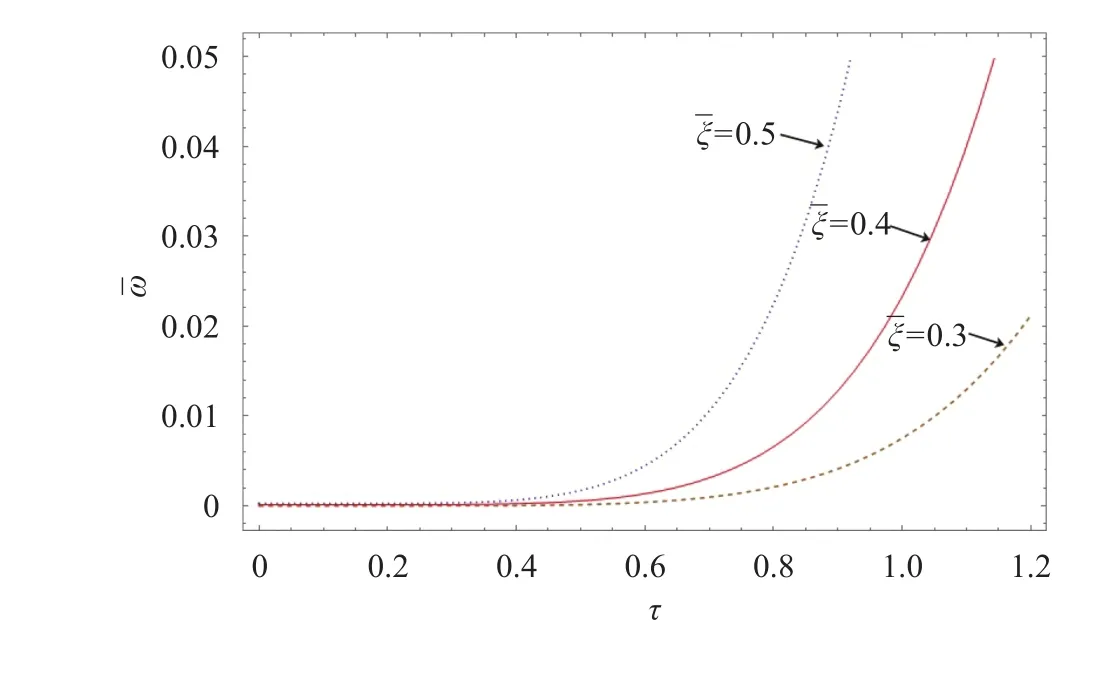
Fig. 6. Thermal deflection along timeτ for differen

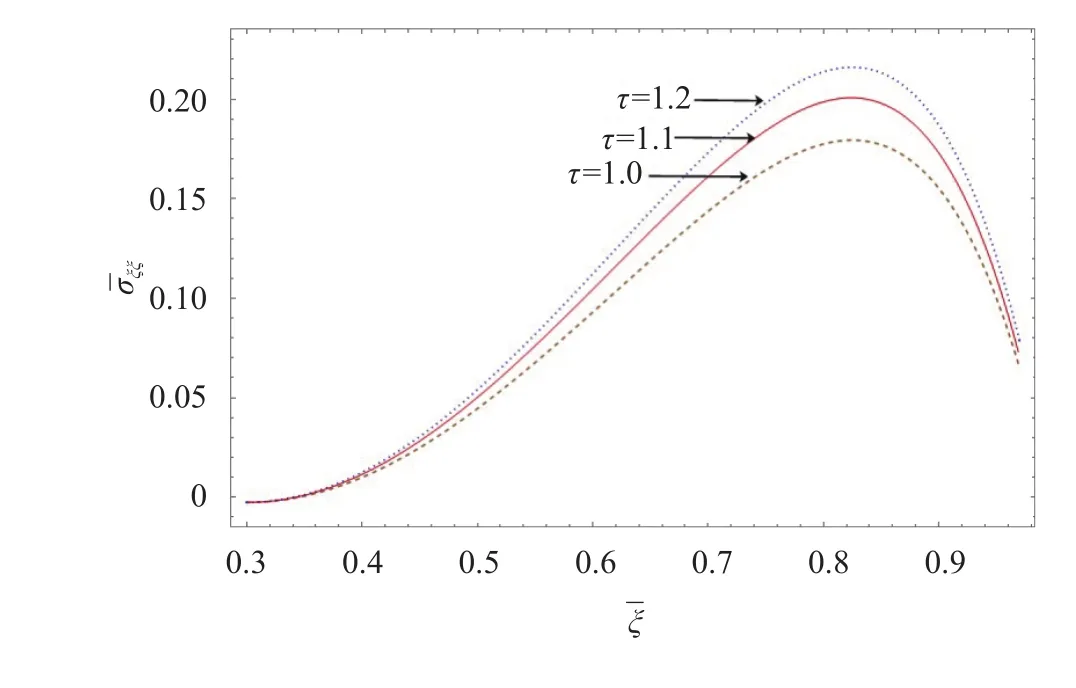
Fig. 7. Radial stress along radial direction for different.

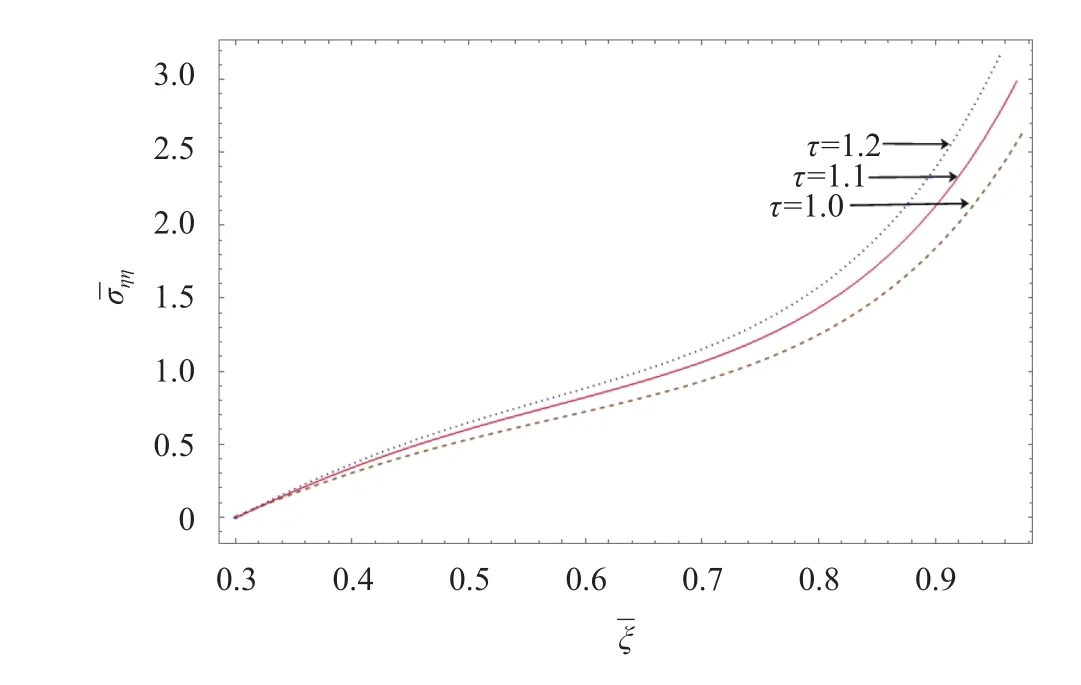
Fig. 8. Tangential stress along radial direction for different.

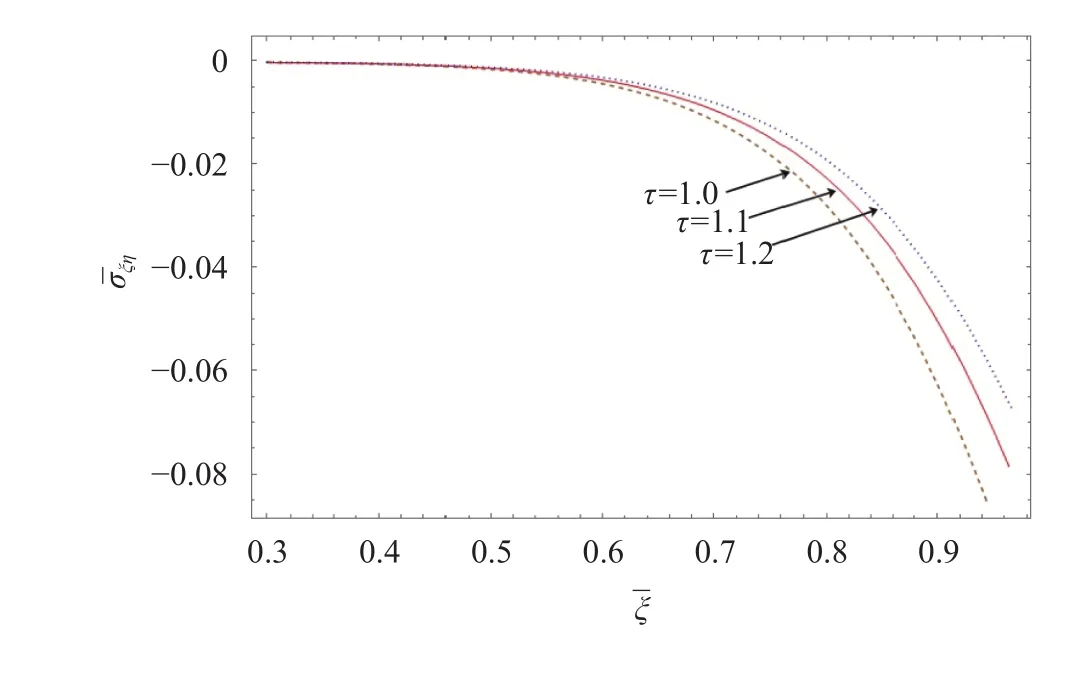
Fig. 9. Shear stress along radial direction for different.

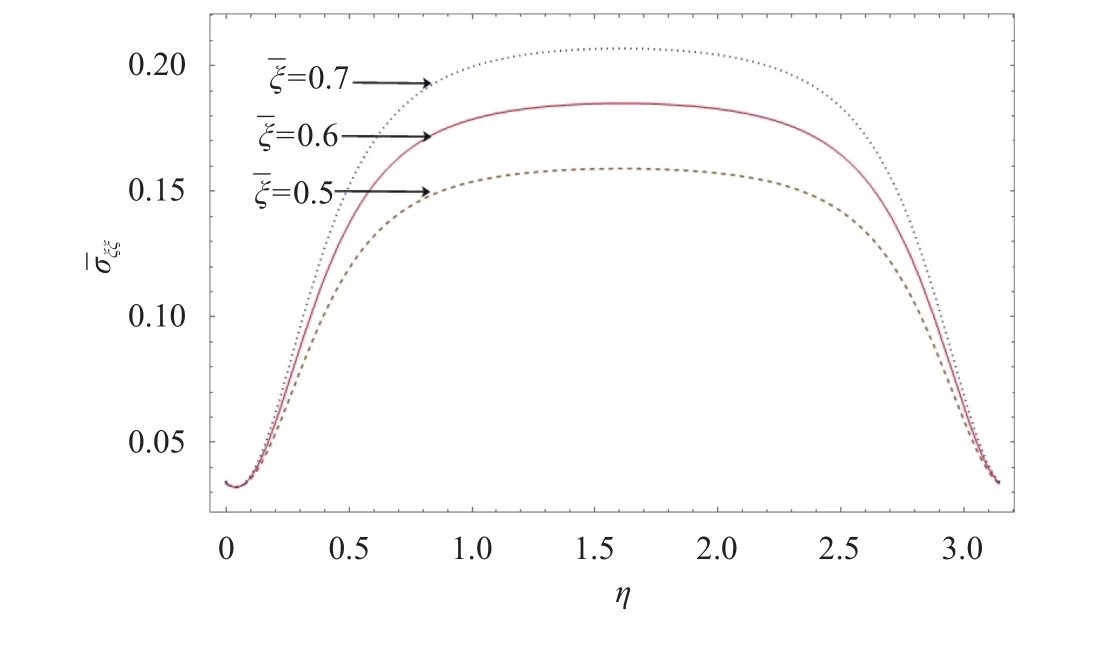
Fig. 10. Radial stress along angular direction for different.

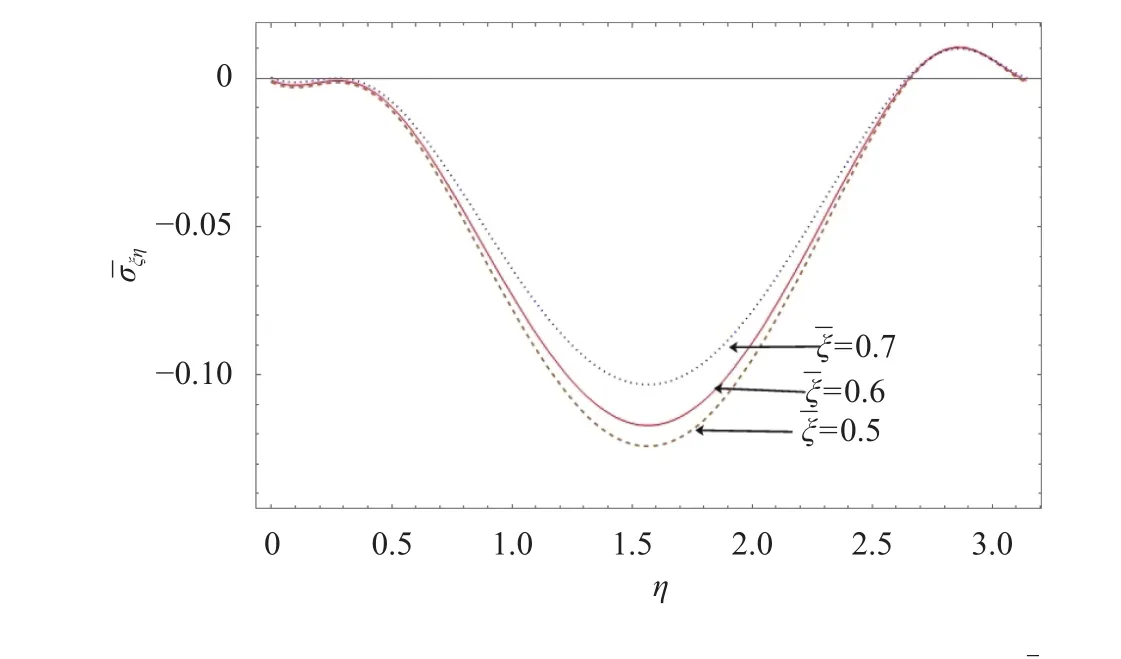
Fig. 11. Shear stress along angular direction for different.

Figures 10 and 11 illustrates the thermal radial stress,shear stressalong the angular direction for different values of. it is evident from the Fig. 10 that at the early stage, radial stress increases gradually and maximum radial stress occur at the midcore and suddenly attains minimum value. The similar curve nature was observed for the angular stress along the angular direction for different values ofand has been omitted here for the sake of brevity. It is observed from Fig. 11 that shear stress has significant influence of negative forces at the mid-core forη- direction.

Particular cases:

Meanwhile, above method can be readily applied to degenerate the other exciting cases also. For example, we consider the three following results as

Case 1:

Let us consider the case in which the applied pressure is one whose intensity decreases exponentially with the time and acts on a circular line and taking sectional heat supply with uniform temperature distribution assuming thatis constant, that is to say

By substitution of this expression (35) into Eq. (28), we arrive at the result

Case 2:

Let us consider the case in which the applied pressure and sectional heat supply whose intensity is of sinusoidal type with the time and acts on a circular line and taking sectional heat supply with uniform temperature distribution assuming thatis constant, that is to say

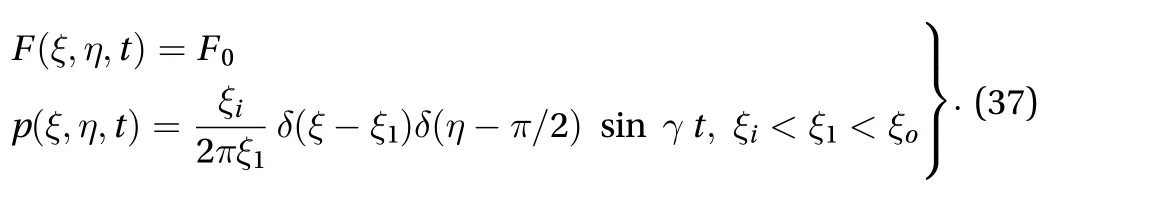
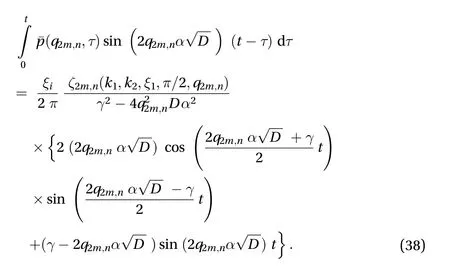
By substitution of this expression (38) into Eq. (28), the solution is

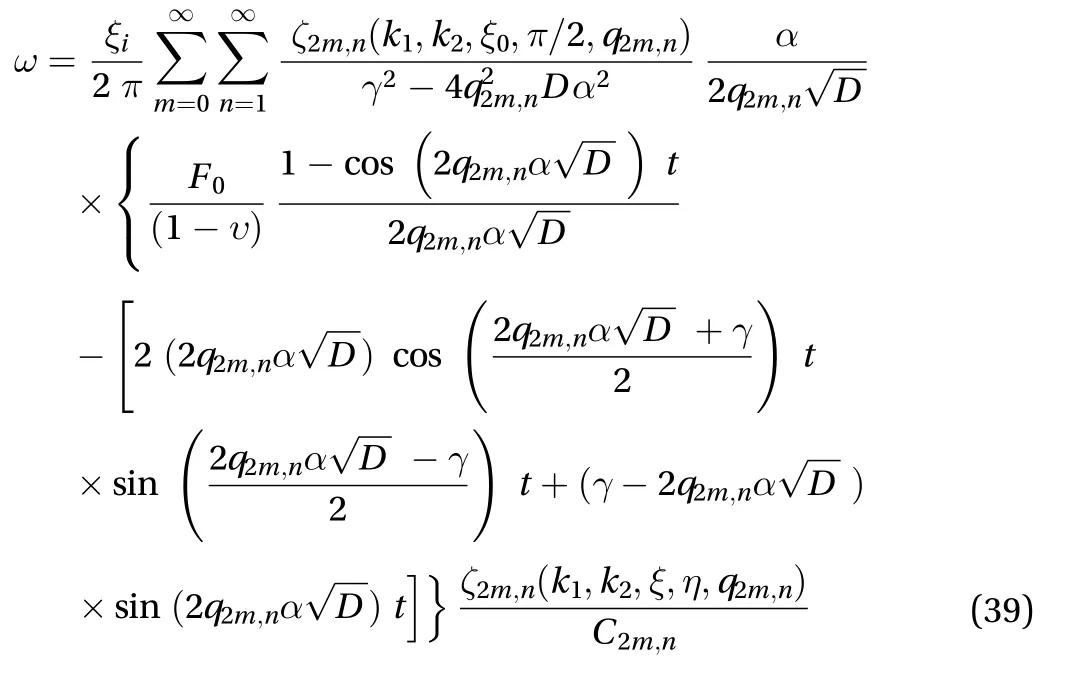
Case 3:

Now, we shall study the vibrations produced in the plate by application of a pressure and sectional heat supply whose intensity is constant type, that is to say

Then the solution takes the appearance as

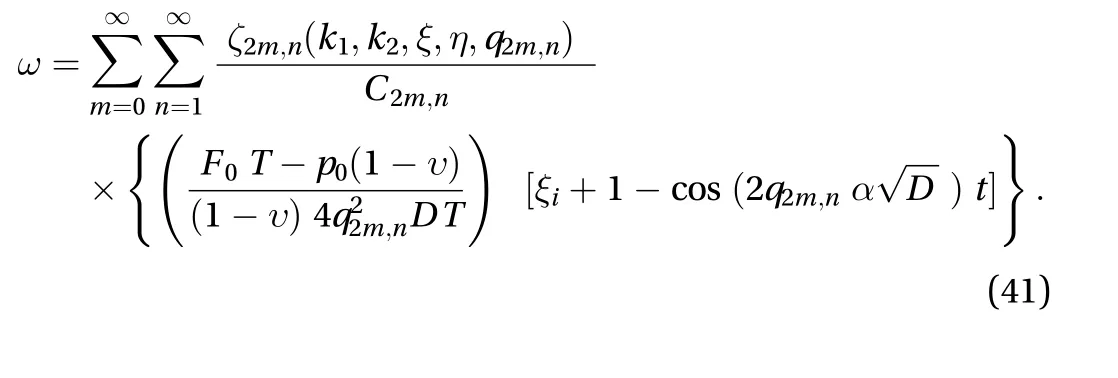
Case 4: Thermal buckling(as a special case with no foundation)

Assuming the harmonic vibration of the natural angular frequency and substitutingand, into Eq. (7), at the onset of buckling, the differential equilibrium equation can be given as

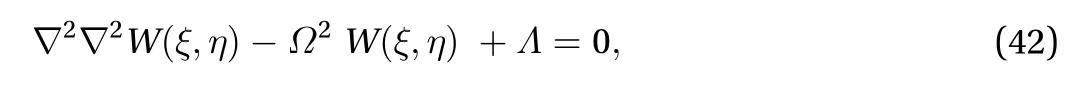
with elastic supports boundary condition

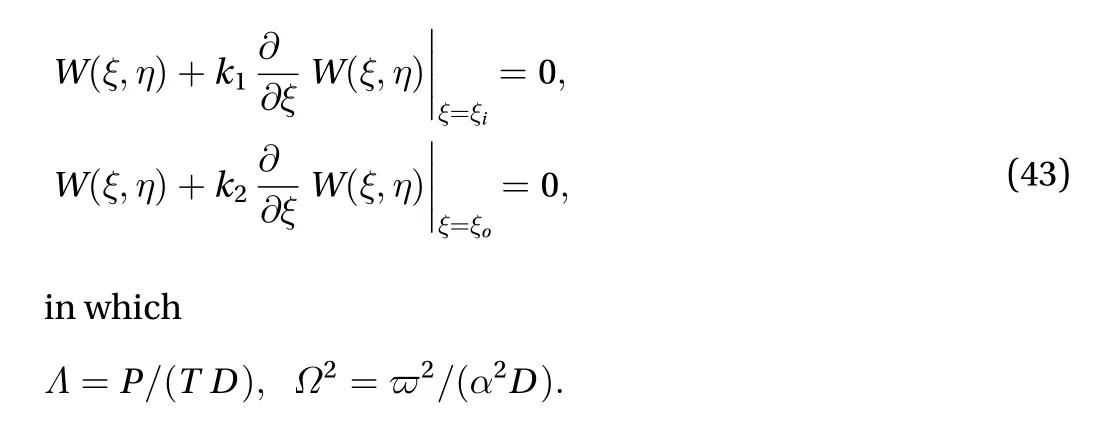
Applying the integral transform defined in Eq. (24) and its inversion theorem which is defined in Eq. (25) to the differential Eq. (42), and taking into account the boundary conditions (43),the solution of the differential equation is obtained as

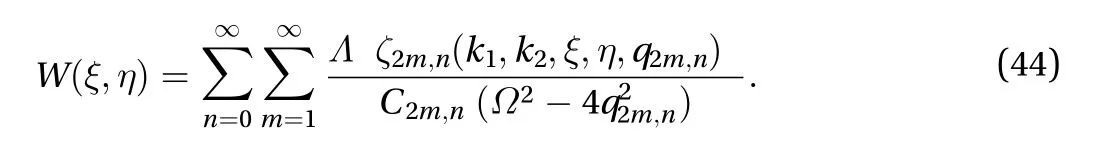
In this article, we have described the theoretical treatment of dynamic thermally induced vibration with its deflection and its associated stresses. The temperature distribution and the deflection in the form of ordinary and modified Mathieu functions are used to determine thermal stresses by proposed operational methods. The analytical technique proposed here is relatively straightforward and widely applicable compared to the methods proposed by other researchers. The results obtained while carrying research are described as follows

• The advantage of this approach is its generality and its mathematical power to handle different types of mechanical and thermal boundary conditions during large deflection under thermal loading.

• The maximum tensile stress shifting from the outer surface due to maximum expansion of an outer part of the plate, its absolute value increases with the radius. This expansion could be due to heat, stress, concentration or available internal heat sources under known temperature field.

• The value of radial stressshows a discontinuity at the boundaries whereas plateau type curve at the middle part along the angular direction.

• Finally, the maximum tensile stress occurs in the circular core on the major axis as compared to the elliptical core indicating the distribution of weak heating. This maximum stress might be due to insufficient penetration of heat through the elliptical inner surface.

• The aforementioned large deflection concept can be beneficial in the field of micro-devices or micro-system applications,planar continuum robots, predicting the elastoplastic bending and so forth.

Appendix

(I) In order to solve hyperbolic type of differential equation oforder as given by

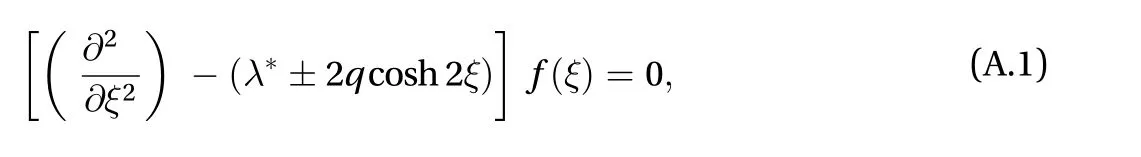
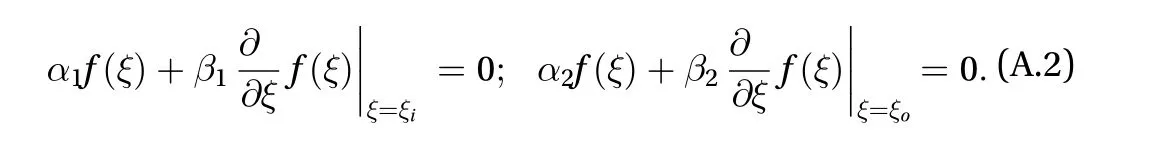
We firstly introduce the integral transform of orderover the variableas

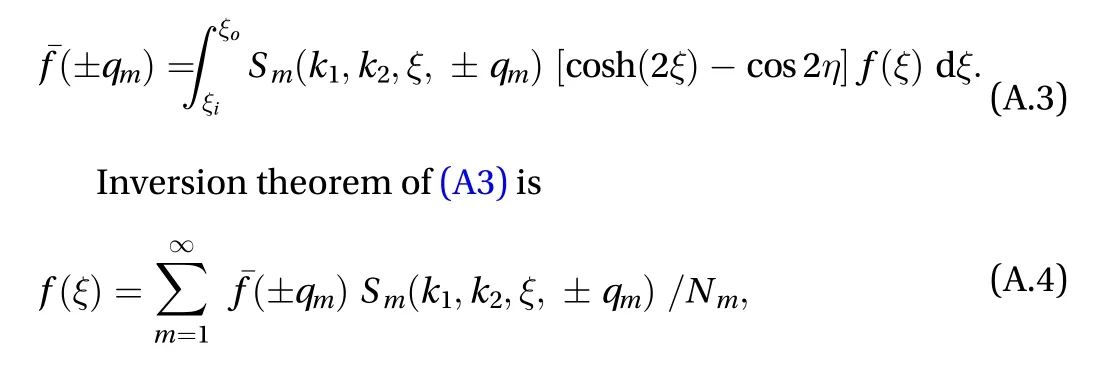
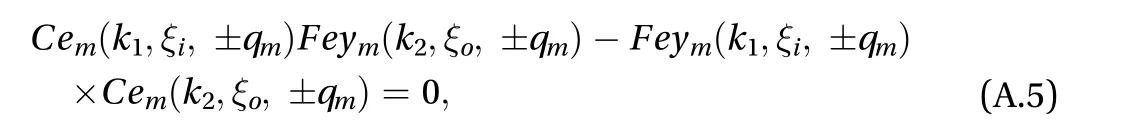
where the kernel is defined as

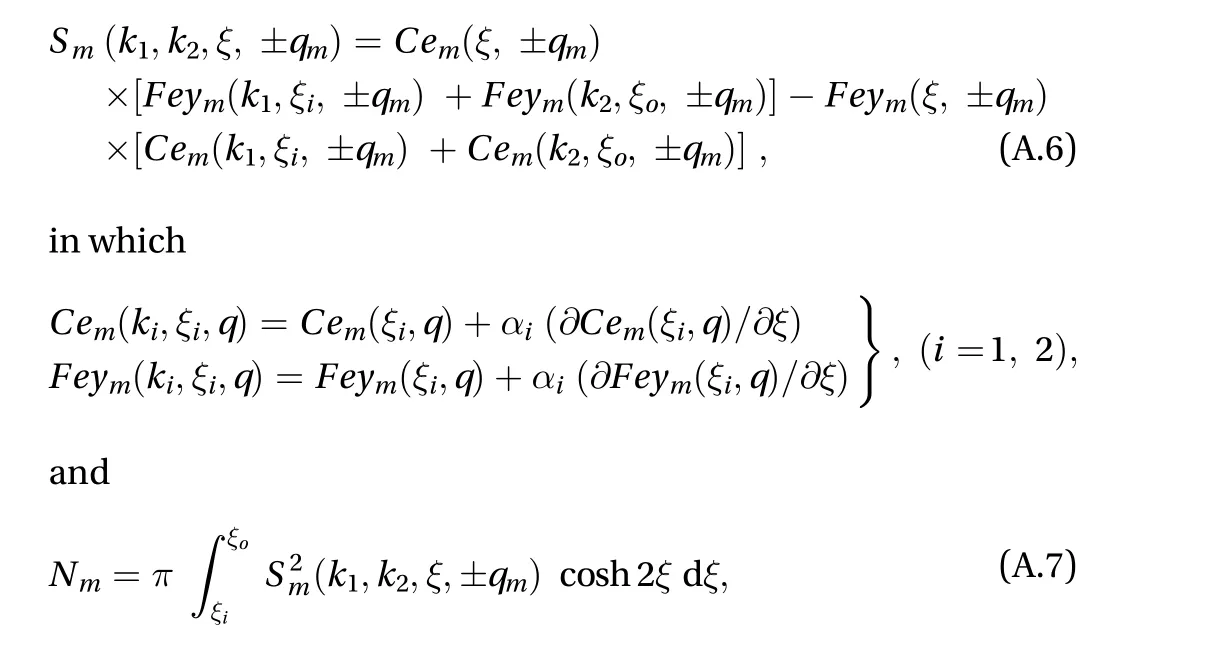
(II) Now considering an another integral transform proposed by Sugano [23] that can be defined as

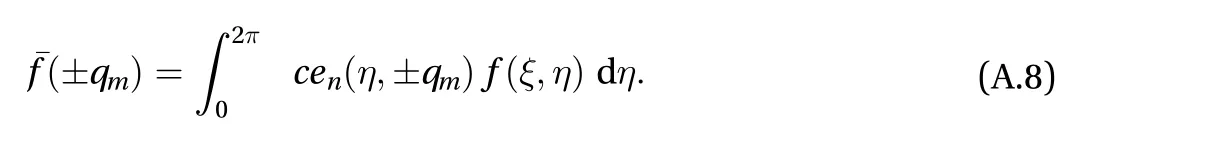
Inversion theorem of (A7) is

(III) Analogous to Mathieu transform defined by Gupta [22,pp.780], we introduce a finite transform which contains a unified kernel as

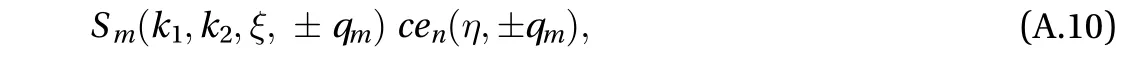
(IV) As a prerequisite integral transform proposed by the author [19], the kernelcan be defined taking into account the boundary conditionsand

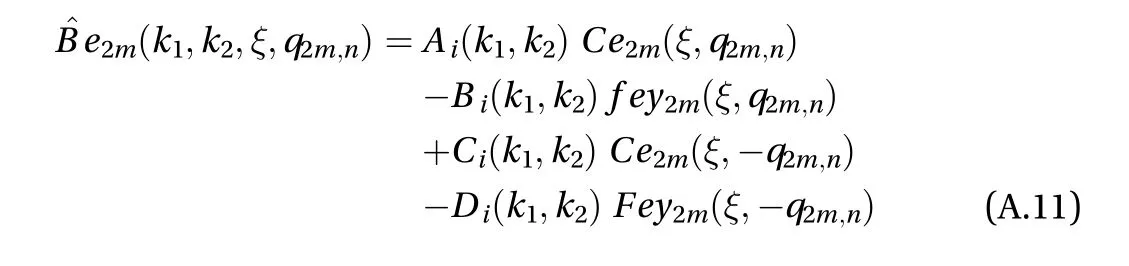
[1]W. Q. Chen, J. Ying, Q. D. Yang, Free vibrations of transversely isotropic cylinders and cylindrical shells, Journal of Pressure Vessel 120 (1998) 321–324.

[2]K. Sato, Free vibration analysis of a composite elliptical membrane consisting of confocal elliptical parts, J. Sound Vib. 34(1974) 161–171.

[3]K. Sato, Forced vibration analysis of a composite elliptical membrane consisting of confocal elliptical parts, J. Phys. Soc.Jpn. 40 (1976) 1199–1206.

[4]J. R. Hutchinson, S. A. El-Azhari, Vibrations of free hollow circular cylinders, J. Appl. Mech. 53 (1986) 641–646.

[5]C. B. Y. Yii, G. R. Buchanan, The effect of the Poisson ratio on the vibration of hollow circular finite-length cylinders, J. Sound Vib. 248 (2001) 187–194.

[6]M. El-Raheb, Transient response of a hollow cylinder with radial and axial material inhomogeneity, J. Acoust. Soc. Am. 119(2006) 2738–2749.

[7]G. C. Gaunaurd, G. C. Everstine, Elasticity solution for an axially compressed and encased cylindrical specimen, Int. J.Mech. Sci. 49 (2007) 116–121.

[8]S. M. Hasheminejad, Y. Mirzaei, Free vibration analysis of an eccentric hollow cylinder using exact 3D elasticity theory, J.Sound Vib. 326 (2009) 687–702.

[9]N. A. Haider, H. N. Ali, Modal interactions in the vibrations of a heat annular plate, International Journal of Non-Linear Mechanics 39 (2004) 1671–1685.

[10]J. Kidawa-Kukla, Application of the Green’s function method to the problem of thermally induced vibration of a circular plate,Scientific Research of the Institute of Mathematics and Computer Science 1 (2010) 53–60.

[11]X. Yao, Q. Han, L. Dai, Free vibration of elliptical plates in uniform temperature field, Proceedings of international design engineering technical conferences & computers and information in engineering conference, Long Beach, California, USA,September 24-28 (2005) 1-6.

[12]H. M. Youssef, K. A. Elsibai, Vibration of nano beam induced by ramp type heating, World Journal of Nano Science and Engineering 1 (2011) 37–44.

[13]R. K. Bera, Thermally Induced Vibration-Elliptic Plates, in R. B.Hetnarski (ed.), Encyclopedia of Thermal Stresses, Springer,Dordrecht, (2014) pp. 5522–5537.

[14]S. M. Hasheminejad, S. Rezaei, P. Hosseini, Exact solution for dynamic response of an elastic elliptical membrane, Thin-Walled Structures 49 (2011) 371–378.

[15]D. D. Ebenezer, K. Ravichandran, Free and forced vibrations of hollow elastic cylinders of finite length, J. Acoust. Soc. Am. 137(2015) 2927–2938.

[16]S. Kukla, Green’s function for vibration problems of an elliptical membrane, Scientific Research of the Institute of Mathematics and Computer Science 2 (2011) 129–134.

[17]P. Bhad, V. Varghese, L. Singh, Thermoelastic theories on elliptical profile objects: An overview and perspective, International Journal of Advances in Applied Mathematics and Mechanics 4(2016) 12–60.

[18]P. Bhad, V. Varghese, L. Khalsa, Thermoelastic-induced vibrations on an elliptical disk with internal heat sources, Journal of Thermal Stresses 40 (2017) 502–516.

[19]T. Dhakate, V. Varghese, L. Khalsa, Integral transform approach for solving dynamic thermal vibrations in the elliptical disk, Journal of Thermal Stresses 40 (2017) 1093–1110.

[20]N. W. McLachlan, Theory and Application of Mathieu function,Clarendon press, Oxford 298 (1947) 367–368.

[21]P. M. Morse, H. Feshbach, Methods of theoretical physics, Mc-Graw-Hill Book Company, Inc., New York-Toronto-London(1953).

[22]R. K. Gupta, A finite transform involving Mathieu functions and its application, Proc. Net. Inst. Sc., India, Part A 30 (1964)779–795.

[23]Y. Sugano, Y. Kondoh, An analytical solution for a plane thermal stress problem expressed in elliptical coordinates,Transactions of the Japan Society of Mechanical Engineers Series A 54 (1988) 2099–2105.

[24]R. Kumar, N.K. Lamba, V. Varghese, Analysis of thermoelastic disc with radiation conditions on the curved surfaces, Materials Physics and Mechanics 16 (2013) 175–186.