基于神经网络前馈的无人直升机非线性鲁棒控制设计*

鲜 斌， 郑国周， 刘世博

(天津大学 电气与自动化工程学院，天津300072)

0 引 言

作为一种旋翼无人机,无人直升机可实现包括垂直起降、悬停和低空飞行在内的多种机动飞行任务，其在军用、民用领域有着广泛的应用[1,2]。然而，无人直升机是一个非线性、强耦合，且具有多种不确定性的欠驱动系统，针对该系统的控制设计正受到国内外研究机构的广泛关注[3～5]。

线性控制方法是目前无人直升机控制领域应用较多的方法，包括：比例—积分—微分(proportion integration differentiation,PID)控制算法[6]、线性二次型(linear quadratic regulator,LQR)控制算法[7]、H∞控制算法等[8]。然而上述方法控制设计过程中所做的平衡点线性化降低了系统在远离工作平衡点时的控制性能。为提高无人直升机的大范围姿态控制性能，以及实现对系统不确定性的补偿及对外界扰动的抑制，文献[9]基于Backstepping方法设计了无人直升机非线性控制器，实现了直升机的位置与姿态的连续跟踪；文献[10]基于动态反馈线性化对无人直升机的纵向通道进行了非线性控制设计。然而以上的控制设计均以无人机系统参数已知为前提。文献[11] 设计了非线性控制算法实现在无人直升机的质量、惯量矩阵以及气动阻尼不确定下的自适应控制。一些智能控制算法也被应用于无人直升机的控制。文献[12]基于强化学习的神经网络控制设计了无人直升机的姿态与高度控制器，数值仿真验证了设计算法的有效性。文献[13]基于模糊逻辑控制算法设计了无人直升机位置与姿态控制器，仿真显示所设计控制器具有一定扰动抑制能力。

本文针对无人直升机姿态控制设计了一种基于神经网络前馈的非线性鲁棒控制器。设计了三层神经网络对系统中的不确定项进行估计并在控制器中进行不确定性的补偿。此外，控制器包含符号函数积分项，可实现一定程度的扰动抑制。基于Lyapunov分析方法证明了闭环系统的半全局收敛。三自由度无人直升机姿态镇定实验验证了算法的有效性。

1 无人直升机姿态动力学模型

如图1所示，无人直升机可视为一个包含3个平动自由度以及3个转动自由度的刚体，其运动可由两个坐标系表示：右手惯性坐标系FI={oIxTyIzI} 和直升机体坐标系FB={oBxByBzB}。以η=[φθψ]T表示无人直升机的翻滚、俯仰和偏航欧拉角向量，体坐标系到惯性坐标系的旋转矩阵记为R，平移矩阵记为S[3]。

图1 无人直升机示意

直升机姿态动力学模型表示如下

(1)

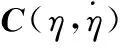
直升机的转矩输入与旋翼挥舞角a,b和尾桨推力TT∈R间的关系可表示如下

τ=S-T(Avc+B)

(2)

式中vc=[abTT]T；A为三维可逆矩阵；B为常数向量。对悬停状态下的挥舞角和尾桨模型作近似化处理得

(3)

根据式(3)，旋翼动力学模型表达式可写为τ=S-T(ACδ+B)，C∈R3×3为常数矩阵。

2 基于神经网络的非线性连续鲁棒控制设计

为实现基于神经网络的直升机姿态鲁棒跟踪控制器设计，定义姿态角跟踪误差e1=ηd-η，其中ηd=[φdθdψd]T为期望姿态轨迹。进行如下假设：期望姿态角有界、光滑且其姿态角加速度有界，即

(4)

式中ζdp,ζdv和ζda为有界正常数。

定义误差的滤波信号

(5)

对r的表达式求导，左乘M(η)并代入姿态动力学模型与旋翼动力学模型，可得

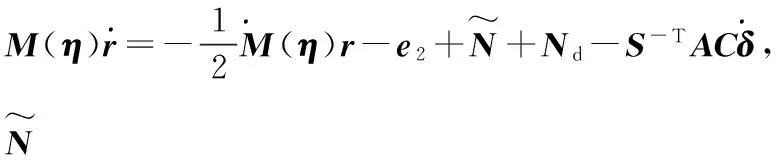
(6)

式中N为定义的辅助函数;Nd为N对应期望姿态轨迹时的值。

根据对参考姿态轨迹的假设式(4)，可证Nd(t),d(t)∈L∞。进一步地

(7)

设计控制输入信号δ(t)如下

(8)

其中非线性鲁棒反馈项u定义如下

u=(Ks+I)r+βSgn(e2)

(9)

对Nd用三层神经网络进行逼近

Nd=WTσ(VTχ)+ε(χ)

(10)

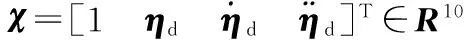
(11)

式中ω1(t)和ω2(t)为辅助滤波信号；φ1和φ2∈R为正常数；T∈R10×10是对角正定的增益矩阵。由式(11)可以得到

(12)

(13)

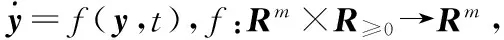
(14)

式中 ∀t≥0，∀y∈D，W1(y)，W2(y)为连续正定函数，W(y)为一致连续半正定函数；若式(14)成立，且y(0)∈S，则下式成立

W(y(t))→0,t→∞

(15)

其中域S定义如下

(16)

式中δ为正常数。

定理: 若控制增益Ks足够大，则本文设计的控制器式(8)保证闭环系统的姿态角收敛，即e1(t)→0,当t→∞。

证明: 将控制器式(8)、式(9)代入姿态动力学方程式(6)，则可得闭环系统姿态动力学方程

M(η)=

βSgn(e2)

(17)

定义辅助能量函数

(18)

根据文献[14]，若选择其中控制器式(8)增益α，β满足

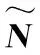
则可证明得到P(t)≥0。

定义Lyapunov函数如下

(20)

其中惯性矩阵M(η)满足以下条件

m1‖ξ‖2≤ξTM(η)ξ≤m2‖ξ‖2

(21)

考虑式(21)，则可对式(18)放缩得到

λ1‖y‖2≤V≤λ2‖y‖2

(22)

式中λ1,λ2为正常数。对V求一阶时间导数，并代入式(17)以及e2,r的定义得

(23)

(24)

更进一步

(25)

考虑式(25)， 若增益矩阵Ks选择满足以下任一条件

(26)

对式(22)～式(26)引用引理1，可得V的上下界函数

W1(y)=λ1‖y‖2,W2(y)=λ2‖y‖2,W(y)=γ‖z‖2

(27)

考虑式(26)，定义区域D

根据式(20)～式(26)，由于

V(y(t),t)∈L∞

可得e1(t),e2(t),r(t)∈L∞。由式(7)、式(17)、式(26)可得(y)∈L∞。根据e2的定义，e2(t)∈L∞，则W(y(t))一致连续。定义区域S如下

则由引理1得，当t→∞,y(0)∈S时‖z‖2→0,e1→0。

若控制增益Ks足够大，吸引域可增大以包含更多的初始状态，如此则可实现系统在半全局的域内姿态角控制误差收敛。

3 非线性姿态控制镇定实验

为验证所设计控制算法的有效性，在自主设计的三自由度实验平台上进行直升机的姿态镇定实验。实验平台如图2所示，其中，无人直升机为TREX—450小型电动直升机，机身长640 mm,主桨长度为710 mm,机体质量为648 g，有效载荷500 g。机载传感器采用Xsens公司的MITI姿态航向参考系统。台架对直升机机体的姿态运动阻碍小，并可将姿态角限制在安全范围内。实验控制器参数为：α=diag{0.9,0.9,0.6},β=diag{0.12,0.12,0.02},Ks=diag{2.24,2.36,0.5},φ1=400,φ2=100,T=diag{45,45,30,45,45,45,45,39,48,45}。

图2 三自由度无人直升机实验平台

控制目标为镇定姿态角至ηd=[0° 0° -100°]T。实验中，无人机经手动起飞，从20 s开始切换进入自动控制状态。为分析控制策略在外界风扰下的鲁棒控制性能，本文设计了扰动对比实验：在60～100 s过程中加入风速约5m/s的阵风扰动。实验结果如图3～图5所示。

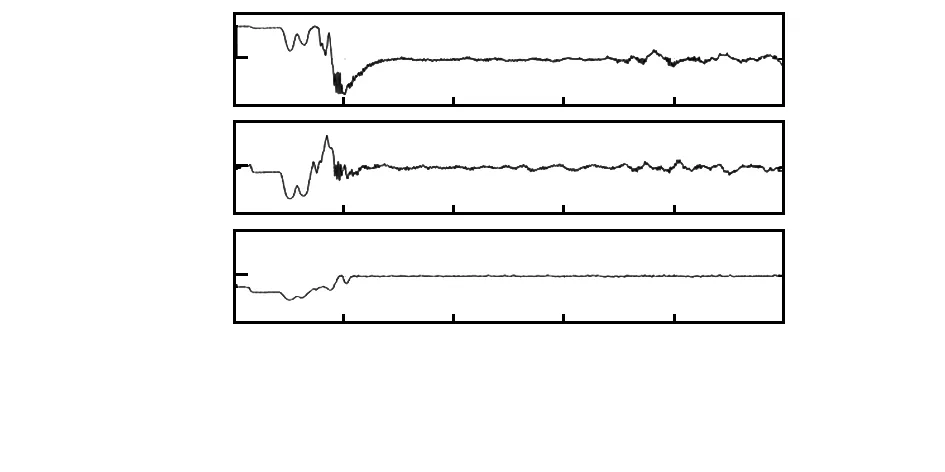
图3 直升机姿态角

图4 直升机姿态角速度

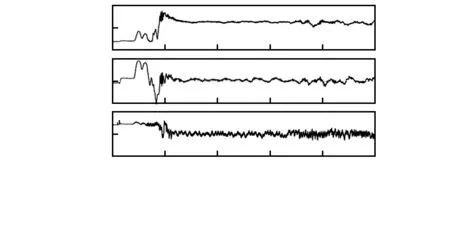
图5 控制输入

从图3可知，当风扰未加入时(对应时间刻度20～60 s)，无人机的姿态镇定取得了较好的控制效果，滚转角、俯仰角和偏航角镇定精度分别控制在±1 °, ±1.2°和±2 °以内。扰动加入阵风扰动时，控制算法实现了良好的姿态控制与扰动抑制效果，相应的姿态角控制精度均为±2°。从图3、图4可知，无人直升机的姿态角速度控制与系统控制输入均在合理范围之内。

4 结束语

针对无人直升机的姿态控制问题，设计了一种基于神经网络前馈的非线性鲁棒控制算法,闭环系统稳定性经Lyapunov分析方法证明。实验结果表明所设计控制算法实现了良好的无人直升机姿态控制效果。

参考文献:

[1] 任小璐，伊国兴，王常虹.一种微小型无人飞行器系统的建模与仿真[J].传感器与微系统， 2008，27(10):36-38.

[2] 郑晓平， 波，李 平，等.小型无人直升机着陆高度单目视觉测量方法[J].传感器与微系统，2013,32(2)：131-134.

[3] Cai G W,Chen B M,Lee T H.Unmanned rotorcraft systems[M].London:Springer-Verlag,2011:259-263.

[4] 王 勇，郭润夏，淡 斌.基于LMI的无人直升机自带解耦鲁棒控制器设计[J].自动化技术与应用，2013,32(7)：10-13.

[5] 杨万君，崔艳华，王旭宁.无人机多机并行测控与数传技术研究[J].无线电工程，2013,43(8)：16-18.

[6] Shim D H,Kim H J,Sastry S.Control system design for rotorcraft-based unmanned aerial vehicles using time-domain system identification[C]∥Proceedings of the IEEE International Conference on Control Applications,2000:808-813.

[7] Schirrer A,Westermayer C,Hemedi M,et al.LQ-based design of the inner loop lateral control for a large flexible BWB-type aircraft[C]∥Proceedings of the IEEE International Conference on Control Applications,2010:1850-1855.

[8] La Civita M,Papageorigious G,Messner W C,et al.Design and flight testing of a gain-scheduledH∞loop shaping(13)for wide envelope flight of a robotic helicopter[C]∥American Control Conference,2003:4195-4200.

[9] Ahmed B,Pota H R,Garratt M.Flight control of a rotary wing UAV using backstepping[J].International Journal of Robust and Nonlinear Control,2010，20(6):639-658.

[10] Morales J G B,Cortes H R,Linares R C.Nonlinear control for the longitudinal dynamics of a small scale helicopter[C]∥European Control Conference,2013:3870-3875.

[11] Diao C,Xian B,Yin Q,et al.A nonlinear adaptive control approach for quadrotor UAVs[C]∥Proceedings of the 8th Asian Control Conference,2011:223-228.

[12] Lee D J,Bang H.Reinforcement learning based neuro-control systems for an unmanned helicopter[C]∥International Conference on Control,Automation and Systems,2010:2537-2540.

[13] Limnaios G,Tsourveloudis N.Fuzzy logic(13)for a mini coaxial indoor helicopter[J].Journal of Intelligent & Robotic Systems,2012,65(1):187-201.

[14] Xian B,Dawson D M,Queiroz M S.A continuous asymptotic tracking control strategy for uncertain nonlinear systems[J].IEEE Transactions on Automatic Control,2004,49(7):1206-1211.