一种针孔相机与三维激光雷达外参标定方法*
2018-04-09正勇卜春光
正勇,卜春光, 刘 宸
(1.中国科学院 沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;2.中国科学院大学,北京 100049; 3.沈阳理工大学 机械工程学院,辽宁 沈阳 110016)
0 引 言
外参标定方法可以分为在线标定[1~3]与离线标定两大类。在线标定法是在无人车运行过程中实时校准外参矩阵,能够修正行驶过程中颠簸等因素造成外参偏移,但需要通过离线标定或者人工测量的方式得到初始值以提高收敛速率。离线标定分成如下三类:棋盘格法;特殊几何外形标定体法;角点法。
Zhang Q[4]提出了一种基于黑白棋盘格的外参标定方法[5],方法简单可靠,但该方法并不能直接得到完整的旋转矩阵,并不是最优的三维旋转群SO(3),另外该方法通过代数方法推导而来,没有明确的几何意义。Park S U等人[6]将Zhang Q的方法推广至三维激光雷达与相机标定问题,但未优化标定结果,也未对标定参数、结果等进行分析。Vasconcelos F等人[7]提出了一种新的基于棋盘格的二维激光雷达与相机标定方法[8],方法较Zhang Q的方法有更精确的初始解,可以有效降低采样帧数较小情况下迭代优化过程中解发散的概率,但计算量大,整个算法也较为复杂。Unnikrishnan R等人[9]在CMU的2005年技术报告中提出了一种基于平面对应性的三维激光雷达与相机的外参标定方法,利用平面对应性分别求解平移与旋转分量,求解公式十分简洁,但也存在一些不足:利用数学方法推导出求解公式,求解过程不直观明了;未分析外参精度;未分析失效情况;只优化外参矩阵,未利用点云、图像数据对内外参进行全局优化。
本文针对对偶空间中面变换矩阵的分解,提出了一种新的基于平面对应性的外参标定方法。该方法求解原理、推导过程简单,更加简单易懂。仿真结果表明:本文方法有很好的初始解,在样本数量较小的情况下仍然可以得到稳定精确的解。
1 外参求解
图1为包含相机、三维激光雷达、棋盘格标定板的标定系统。考虑原点分别在O、O′的相机坐标系和激光坐标系。外参标定问题即为求解欧几里得变换T,使得
(1)
式中Q,Q′分别为点在相机坐标系和激光坐标系中的非齐次表示;R为3×3旋转矩阵;t为3×1平移向量。
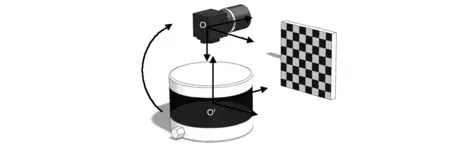
图1 坐标系定义
1.1 线性求解
如果2个笛卡尔坐标系下点的射影变换方程为X′=Y×X,在该变换下面П变换为[9]
Π′=T-T×Π
(2)
对于外参标定问题,变换T为欧氏变换矩阵,在对偶空间中
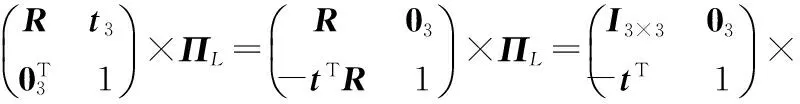
(3)
使用张正友相机标定法和随机一致性采样(random sample consensus,RANSAC)[10]分别从图像和点云中提取棋盘面在相机坐标系和激光坐标系下的齐次表示ΠC,ΠL
Si=-tTRΠLi
(4)
(5)

本文提出的外参矩阵标定算法可以分解成:
1)使用RANSAC和张正友相机标定法分别计算出棋盘面在激光坐标系和相机坐标系下的齐次表示ΠLi,ΠCi,其中,i=1…N;


4)联立式(4)、式(5),计算欧氏矩阵平移分量。

图2 对偶空间中欧氏变换分解
1.2 非线性优化
使用非线性优化的方法最小化棋盘格在相机和激光坐标系下的重投影误差以提高外参、相机内参标定精度。
(6)

e=κeL+eC
(7)
式中κ为权值,相机成像重投影误差一般为0.2个像素,当激光雷达的误差为±0.03 m的时候,κ可以选择10。最后,使用Levenberg-marquardt方法优化初始标定结果。
1.3 失效分析
1)如果某次标定样本所有帧的棋盘面相互平行或者趋近平行,那么面在对偶空间中的非齐次表示归一化后将重合或者趋近重合,因此,无法标定出旋转分量。
2)棋盘面经过相机或者激光雷达原点,这种情况下无法提取棋盘面在激光或者相机坐标系下的表示。若已知面坐标,理论上可以求解出外参的旋转分量,但不能求解平移分量。
2 仿真实验
2.1 仿真参数
为了对比不同算法标定精度,在MATLAB下进行了仿真实验,仿真参数如表1所示。
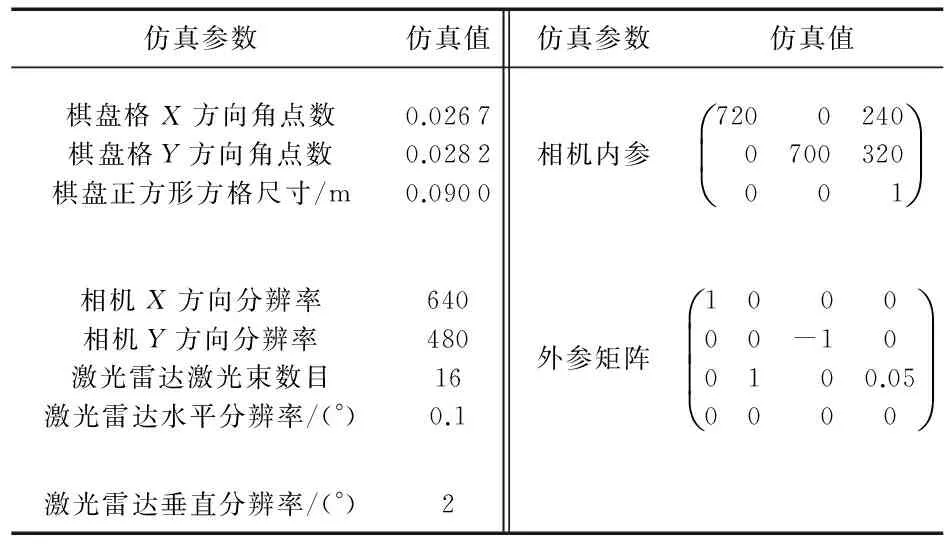
表1 MATLAB仿真参数
以激光坐标系Y′O′Z′作为垂直面,X′O′Y′作为水平面,在水平视场角60°、垂直视场角60°内,生成一距离激光坐标系原点2~4 m的点为棋盘格坐标系原点,棋盘格坐标系相对于激光坐标系RPY角分别在±30°,±90°,90°±30°范围内,如果棋盘格所有角点都能在相机成像面上成像,则记录一帧数据。
对于原始不含噪声的仿真数据,本文方法能准确标定出外参矩阵。
对棋盘格角点添加±0.5个像素的随机噪声,每个激光束采样到的距离信息添加±0.03 m的随机噪声以模拟真实数据。
2.2 仿真结果
仿真实验对比3种标定算法未优化结果:本文方法、文献[8]方法、文献[5]方法。仿真系统对标定结果的评价函数为
(8)
(9)
(10)
式(8)~式(10)分别为外参矩阵平移分量、旋转分量、外参矩阵与真值差的2-范式。
图3、表2分析了采样帧数对标定结果的影响(每组实验重复500次)。根据式(10)的评价指标,随着采样帧数增加,3种算法500次实验误差均值、均方根值均在降低,当采样帧数大于11帧时,标定误差趋于稳定。

图3 不同采样帧数对变换矩阵影响

采样帧数均值本文方法文献[8]文献[5]均方根本文方法文献[8]文献[5]50.0700.0723.0800.0870.0924.42060.0530.0540.9620.0450.0461.48270.0430.0440.4050.0290.0290.60780.0370.0390.2190.0310.0320.29190.0320.0340.1370.0220.0230.181100.0280.0290.0990.0190.0190.108110.0270.0280.0770.0170.0170.073120.0230.0240.0660.0130.0140.055130.0230.0240.0530.0140.0150.047140.0210.0220.0470.0120.0130.035150.0210.0220.0450.0120.0120.033
图4分析了不同算法标定精度。每次采样11帧数据,根据式(8)~式(10)评价3种算法平移分量、旋转分量、变换矩阵误差,重复实验500次。通过对比可以看出,相对于文献[5]的方法,本文以及文献[8]的方法有明显的优势。对比表3~表5的数据,相对于文献[8]的方法,本文方法在平移分量与整个变换矩阵精度上稍占优势,在旋转分量上精度稍低,2种方法精度相同。

图4 不同算法标定误差对比
图5为根据式(7)计算的重投影误差。随着采样帧数的提高,重投影误差逐渐降低。从重投影误差也可以看出本文与文献[8]精度上明显优于文献[5]的方法。
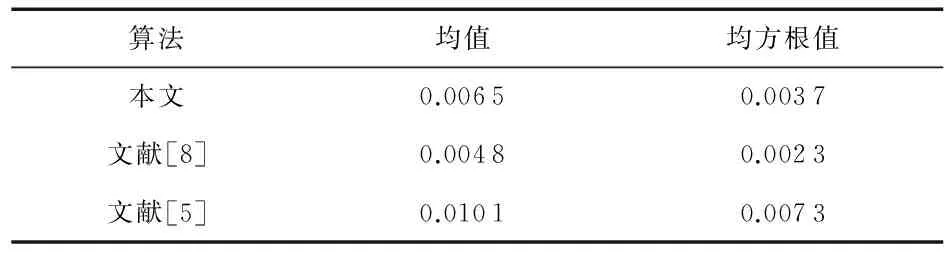
表3 不同算法旋转误差对比
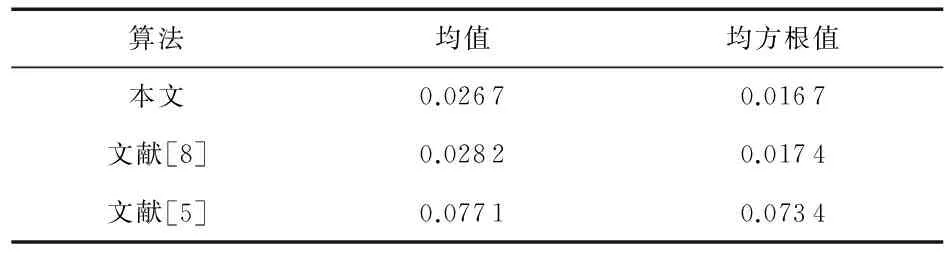
表4 不同算法平移误差对比

表5 不同算法变换矩阵误差对比

图5 重投影误差
图6分析了本文方法旋转分量、平移分量、变换矩阵精度随采样帧数提高的变化情况。采样帧数较少时,外参矩阵精度较低,当采样帧数增加时,误差均值、均方根值均降低,说明标定误差在逐步降低并且标定一次获取高精度标定结果的概率在增加,当采样帧数大于11时,解的精度趋于稳定,但依旧随着采样帧数的增加而缓慢提高。

图6 不同采样帧数对本文方法3种误差的影响
2.3 仿真结果分析
仿真实验对比的3种算法均基于平面对应性。本文与文献[8]的方法未优化解精度相似,且明显优于文献[5]的方法。经分析比较,文献[5]采用了原始的点云数据,而另外2种方法采用了最小二乘法提取出的平面坐标,消除了部分噪声,因此,相同数据源下精度更高。
3 真实数据标定
本文方法在如图7(a)所示的转台上测试,转台使用Pointgrey FL3—GE—03S2C—C工业千兆以太网相机以及Velodyne VLP—16三维激光雷达。激光雷达共有16个激光束,垂直分辨率为0.2°,水平分辨率为0.1°~0.4°,最远探测距离为100 m并且能保证典型距离下±0.03m的精度。相机的分辨率为640×480,搭配工业低畸变焦距4 mm的镜头。黑白棋盘格标定板尺寸为9×9,每个棋盘格的大小为90 mm×90 mm。获取12帧图像、点云数据,人工指定棋盘面在点云中的位置,使用0.03 m允许误差的RANSAC算法分割出棋盘面。图7(b)为激光雷达采集的一帧完整数据,方框标记为标定板在点云中的位置。图7(c)为根据本文方法标定出外参矩阵后将激光点云投影到图像上的结果,从棋盘格边界位置可以看出,标定结果较为精准。图8为本次标定实验优化算法每次迭代后的重投影误差曲线,取κ=10。

图7 实验台及投影结果

图8 重投影误差随迭代次数变化曲线
4 结 论
提出了一种新的基于平面对应性的方法标定三维激光雷达与相机之间的外参矩阵,引入了对偶空间中面变换矩阵的分解,求解过程直观明了。利用该方法原理解释了外参标定过程中失效场景原因。对比3种算法标定误差的仿真实验表明:本文方法可以得到高精度外参矩阵,且在数据较少(最少3帧)的情况下依然可以标定出外参。利用点云、图像数据对内外参进行全局优化并使用真实数据验证了本文算法可靠性。
参考文献:
[1] Rodríguez-Garavito C H,Ponz A,García F,et al.Automatic laser and camera extrinsic calibration for data fusion using road plane[C]∥2014 the 17th International Conference on Information Fusion,IEEE,2014:1-6.
[2] Levinson J,Thrun S.Automatic online calibration of cameras and lasers[C]∥Robotics:Science and Systems,2013:24-28.
[3] 王伟华,宋申民.一种简易的摄像机标定方法[J].自动化技术与应用,2010,29(1):101-103.
[4] Zhang Q,Pless R.Extrinsic calibration of a camera and laser range finder(improves camera calibration)[C]∥Proceedings of 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems,IROS 2004,IEEE,2004:2301-2306.
[5] Zhang Z A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.
[6] Park S U,Chung M J.Extrinsic calibration between a 3D laser scanner and a camera using PCA method[C]∥2012 the 9th International Conference on Ubiquitous Robots and Ambient Intelligence(URAI),2012.
[7] Vasconcelos F.A minimal solution for the extrinsic calibration of a camera and a laser-rangefinder[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2012,34(11):2097-2107.
