基于Lebedev网格的TTI介质二维三分量正演模拟

刘东洋　彭苏萍　师素珍　赵太郎

(中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083)

1　引言

随着地震勘探面临的勘探目标越来越复杂，地震波在各向异性介质中的传播规律成为研究热点。沉积岩地层由于受矿物颗粒、裂隙、晶体等的排列和周期性的薄层等因素的影响而普遍呈现各向异性特征。在理论研究中通常使用VTI和HTI介质模型分别描述由周期性薄互层和由定向排列的垂直裂隙引起的各向异性介质。但是当介质的本构坐标系与观测坐标系存在一定角度时就会引起极大的观测误差，因此需要根据Tsvankin等[1]的研究，对VTI介质进行坐标变换，以获得TTI介质的弹性系数矩阵。

常采用数值模拟方法研究地震波传播规律，有限差分法是其中最常用的方法。Alterman等[2]最早给出了均匀各向同性介质的二维二阶波动方程有限差分算法。Virieux[3，4]基于一阶速度—应力方程提出了交错网格方法，将应力和速度分别定义在不同的网格体系上，并对时间进行交错，与常规网格法相比差分精度提高了4倍。Dalain[5]给出了求解声波方程的高阶差分方法，该方法降低了单位波长内的网格点数，提高了计算效率。Graves[6]提出了三维交错网格有限差分模拟方法。董良国等[7]提出了一阶弹性波波动方程交错网格高阶有限差分解法，同时给出了相应的稳定性条件。裴正林等[8-10]采用高阶交错网格有限差分算法对三维各向异性介质进行数值模拟，并推导了三维各向异性介质完全匹配层(PML)边界条件公式和相应的交错网格差分格式。李东等[11]利用交错网格有限差分法对煤储层双相各向异性介质进行数值模拟，并用于煤层气富集区。综上所述，对于各向异性介质的研究多采用交错网格方法，但是在交错网格中每个变量的不同分量都是交错定义的，对于没有定义的点需要进行变量插值，从而降低了模拟精度。为此，笔者在前人的研究基础上，给出了TTI介质的二维三分量应力—速度弹性波方程的Lebedev网格有限差分解法，并对地震波在单层各向异性介质以及含透镜体的复杂介质中的传播特征进行了数值模拟，验证了Lebedev网格有限差分算法的有效性。

2　方法原理

2.1　TTI介质二维三分量应力—速度方程

(1)

式中：v、σ分别代表速度和应力；Cij为TTI介质弹性张量系数矩阵的元素。

2.2　TTI介质Lebedev网格有限差分格式

在使用常规交错网格进行数值模拟时，由于需要对未定义在交错位置上的变量进行复杂的插值计算，极大地降低了运行效率，同时引入了数值误差，降低了运算精度[12，13]。为此，人们基于Lebedev的思想提出了Lebedev网格[14-16]，该网格的特点是将应力、速度分量定义在同一网格上，但是应力、速度分量在网格点上交错分布，相当于把需要插值的分量直接在网格点上定义，可以准确计算每个变量在各个方向的数值，而无需进行插值。根据Lebedev网格变量示意图(图1)，可对式(1)进行网格离散，由此得到Lebedev网格机制下TTI介质波动方程的有限差分格式

(2a)

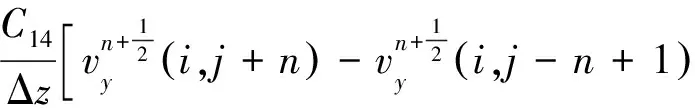
(2b)

图1　Lebedev网格变量分布示意图

2.3　稳定条件

在数值模拟过程中，如果选取的离散参数不合适，那么数值计算结果会出现巨大偏差，严重时会造成数值溢出而使计算无法进行，因此稳定性问题是数值模拟过程中求解波动方程的重要问题。对于Lebedev网格有限差分技术，Lisitas等[16]给出了时间二阶、空间2N阶差分精度下的Lebedev网格稳定性条件

(3)

式中： Δt为时间步长；vmax=max(vi)(i=1、2、3)表示三种波在TTI介质中传播的最大速度；Δx、Δy、Δz分别为对应方向的空间步长。

由于Lebedev网格是在传统交错网格未定义的网格点上增加了相应变量，因此这两种网格的稳定性条件基本相同，但是在理论上Lebedev网格稳定性条件的适用性更广泛[18-21]。

2.4　吸收边界条件

在数值模拟过程中，由于计算空间有限，所以使模拟波场在传播到计算边界时会发生反射现象，增加了波场干扰，从而影响模拟效果。因此需要引入人工边界，使波场在边界附近的能量逐渐衰减。由于在特定情况下传统的PML吸收边界条件会因为具有指数增长解而存在不稳定现象，因此本文采用多轴完全匹配层(M-PML)进行边界处理。M-PML吸收边界条件由传统的PML吸收边界条件发展而来，传统的PML吸收边界条件方法通过引入衰减因子d、分裂变量而实现。M-PML吸收边界条件方法是对传统PML吸收边界条件进行一般化扩展，并在多个方向上同时引入衰减因子。以垂直x轴的匹配层中的vx为例，有

(4)

式中：vx1、vx2分别为垂直于边界和平行于边界的vx；dx、dz为衰减因子，dx的取法与传统PML中的衰减因子相同，dz=P1*dx(P1为稳定性因子)。

同理，在垂直y轴的匹配层中存在稳定性因子P2，稳定性因子的取值通常根据经验获得，不同介质模型对应的稳定性因子不同，本文的稳定性因子取为P1=P2=0.32。特别地，当稳定性因子都为零时，M-PML吸收边界退化为常规PML吸收边界[17]。

3　正演模拟

3.1　单层介质模型

为了验证Lebedev网格算法的有效性及稳定性，通过模拟TTI介质分析Lebedev网格有限差分技术的模拟效果与波场特征。随着主频升高会使图像分辨率增强，但是过高的主频则会产生严重的数值频散现象。同时子波主频的选取受空间和时间采样间隔的影响，即：当采样间隔较小时需要选取较高的子波主频以提高波形分辨率；当采样间隔较大时可以采用较低的子波主频以压制频散效果。因此在保证模拟质量的前提下，为了尽可能地提高图像分辨率，采用主频为100Hz的Ricker子波，震源位于模型中心，其他物性参数如表1所示，其中Cij表示弹性系数， φ为方位角， θ为极化角。

表1　TTI介质物性参数

注：Cij的单位为109kg·m-1·s-2, 密度ρ的单位为g·cm-3

图2为TTI介质二维三分量波场快照和炮记录。在图中可以清晰地分辨TTI介质中的qP波、qSV波、qSH波，其中x分量(图2a)和z分量(图2c)的纵波能量较强，y分量(图2b)的纵波能量较弱，在TTI介质中存在横波分裂现象，因此三个分量的横波在两个对角线方向出现分叉；从炮记录中可以看出，纵波速度最大，qSH波速度最小，这些特征皆符合波场传播规律，因此Lebedev网格很好地模拟了地震波在TTI介质中的传播特征(图2d～图2f)；地震波沿对称轴方向的传播速度明显小于垂直于对称轴方向，这也从侧面验证了Lebedev网格算法的有效性。

3.2　吸收边界效果分析

为测试M-PML吸收边界处理效果，采用单层TTI介质进行波场模拟。采用爆炸震源激发，震源位于模型中心，主频为80Hz，其他物性参数如表1所示。图3为未加M-PML吸收边界条件的TTI介质二维三分量波场快照和炮记录。由图可见，qP波在边界处产生了强反射现象，由于震源的埋深大于四分之一地震波长，因此在边界位置还产生了qP波虚反射(图3b、图3c)，严重干扰了数值模拟结果。图4为加M-PML吸收边界条件的TTI介质二维三分量波场快照和炮记录，可见边界处的反射波和虚反射全部消失。图5为PML与M-PML吸收边界的x、z分量波场快照。 由图可见，横波在PML吸收边界的左上方出现不稳定波场反射(图5a)，在M-PML吸收边界条件的波场传播较为稳定，未出现杂乱反射(图5b)。因此M-PML吸收边界条件的处理效果较理想。

图2　TTI介质二维三分量波场快照(t=40ms)和炮记录

图3　未加M-PML吸收边界条件的TTI介质二维三分量波场快照(t=100ms)和炮记录

图5　PML(a)与M-PML吸收边界(b)的x(左)、z分量(右)波场快照(t=80ms)

图6　透镜体介质模型示意图

模型尺寸为400m×400m，网格分为两部分，白色区域为TTI介质，黑色部分为透镜体(各向同性介质)，x、z方向的空间采样间隔均为1m，时间采样间隔为0.1ms，采用爆炸震源激发，主频为80Hz，震源位于中心

3.3　透镜体模型

在沉积岩发育地区由于断层、风化和侵蚀等作用的影响，在地下介质中可形成一种中间厚、边缘薄的区域性地带，因形似一枚透镜，故称作透镜体。透镜体一般是由矿物变质形成的，因此研究透镜体模型(图6)可为矿产资源开发提供一定的模型基础。采用非均匀TTI介质进行波场模拟，具体物性参数见表2。图7为非均匀TTI介质在40、50、60ms的x、y、z分量波场快照。由图可见：在40ms时，纵波在透镜体处发生了明显的反射，可以观察到透镜体顶面的反射波(图7a)；在50ms和60ms时，横波在透镜体处也发生反射，同时出现了纵波在透镜体底面的反射波，在透镜体的两端出现绕射波(图7b、图7c)，因此基于Lebedev网格得到的波场快照符合地震波传播规律。

表2　透镜体模型物性参数

注：Cij单位为109kg·m-1·s-2, 密度ρ的单位为g·cm-3

图7　非均匀TTI介质在40ms(a)、50ms(b)、60ms(c)的x(左)、y(中)、z分量(右)波场快照

3.4　Lebedev网格与传统交错网格对比

为验证Lebedev网格的运行优势，应用双层介质模型(图8)从运行效率和差分精度两方面对Lebedev网格与传统交错网格进行对比、分析。图9、图10分别为由传统交错网格有限差分与Lebedev网格有限差分得到的双层各向同性介质在0.4s的x、z分量波场快照，运行时间分别为497.107s和362.068s，故后者的运行效率提高了27%。由图可见：由于数值插值的影响，前者存在明显的数值频散，模拟精度较低，地震波在下层介质中的波形显示也较模糊(图9)；后者基本不存在数值频散，波形显示也较清晰，模拟精度明显提高(图10)。

图8　双层介质模型示意图

设定双层的各向同性介质模型，模型尺寸为400m×400m，模型分为上、下两层，下层介质的速度和密度较大。x、z方向的空间采样间隔均为10m，时间采样间隔为1ms，采用爆炸震源激发，震源位于中心，主频为30Hz

图9　双层各向同性介质传统交错网格有限差分在0.4s的x(a)、z(b)分量波场快照

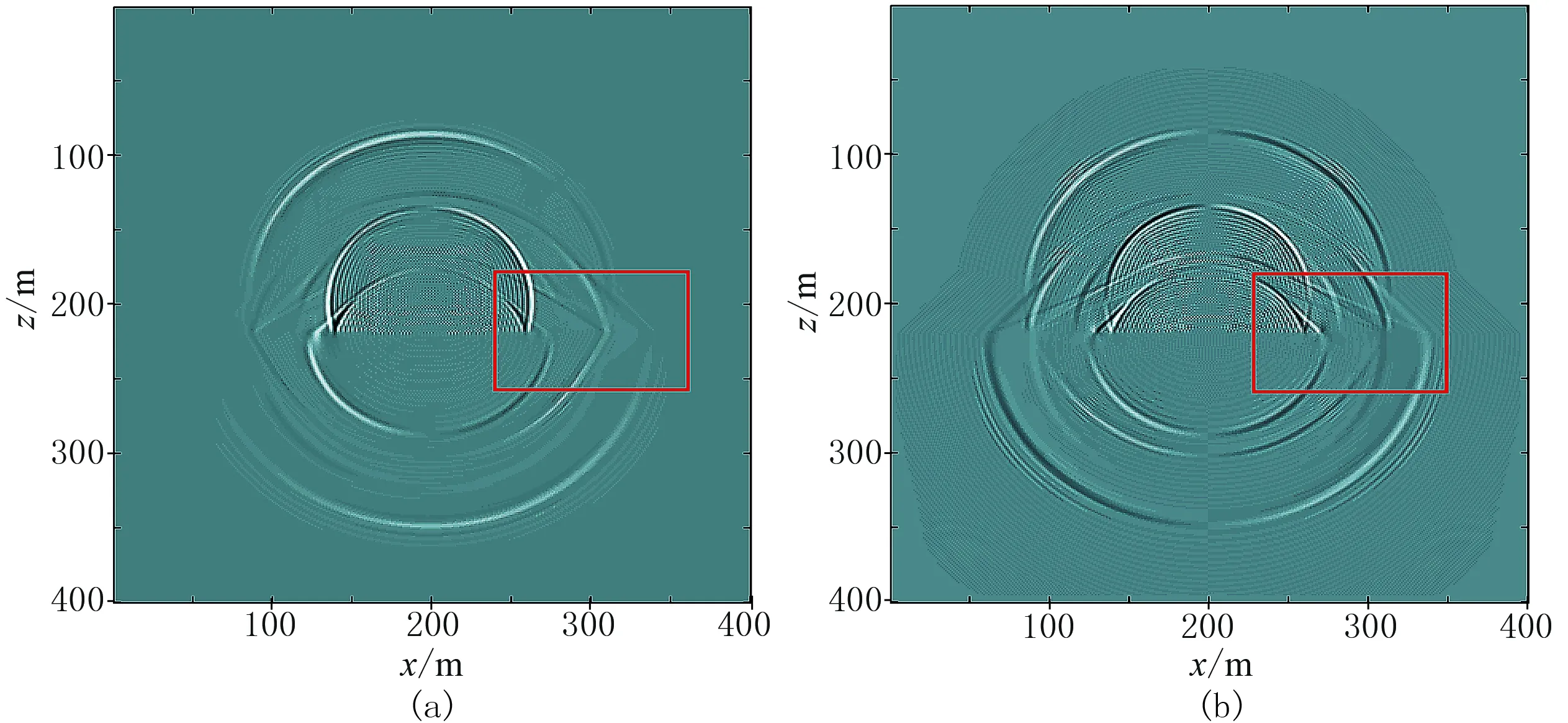
图10　双层各向同性介质Lebedev网格有限差分在0.4s的x(a)、z(b)分量波场快照

4　结束语

文中基于Lebedev网格对TTI介质二维三分量的应力—速度方程进行了高精度差分离散处理，并分别对单层和复杂TTI介质模型进行了正演模拟，得到以下认识：①由于Lebedev网格对各向异性介质的弹性波方程做离散时无需进行波场插值，与传统交错网格有限差分方法相比，模拟精度更高；对TTI介质进行模拟时可以清晰地观察到纵波、快横波和慢横波，并且快、慢横波的偏振方向相反，在单炮记录中观测到的三种波的速度特征也符合波场传播规律。②引入多轴完全匹配层(M-PML)吸收边界条件后，在不影响模拟效果的情况下边界反射现象被有效地压制，因此M-PML吸收边界是一种有效的边界条件。③在复杂介质条件下，使用Lebedev网格的模拟结果依然符合实际情况，因此Lebedev网格适用于各向异性介质模型的波场数值模拟。

[1]Tsvankin I,Thomsen L.Inversion of reflection traveltimes for transverse isotropy.Geophysics,1995,60(4):1095-1107.

[2]Alterman Z,Karal F C.Propagation of elastic waves in layered media by finite difference methods.Bulletin of the Seismological Society of America,1968,58(1):367-398.

[3]Virieux J.SH wave propagation in heterogeneous media: velocity-stress finite-difference method.Geophysics,1984,49(11):1933-1942.

[4]Virieux J.P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method.Geophysics,1986,51(4):889-901.

[5]Dablain M A.The application of high-order differencing to scalar wave equation.Geophysics,1986,51(1):54-66.

[6]Graves R W.Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences.Bulletin of the Seismological Society of America,1996,86(4):1091-1106.

[7]董良国,马在田,曹景忠等.一阶弹性波方程交错网格高阶差分解法.地球物理学报,2000,43(3):411-419.

Dong Liangguo,Ma Zaitian,Cao Jingzhong et al.Study on stability of staggered grid high order difference method for first order elastic wave equation.Chinese Journal of Geophysics,2000,43(3):411-419.

[8]裴正林.三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟.中国石油大学学报(自然科学版),2004,28(5):23-29.

Pei Zhenglin.Numerical simulation of elastic wave equation with staggered grid high-order finite difference method in three dimensional anisotropic medium.Journal of China University of Petroleum(Edition of Natural Science),2004,28(5):23-29.

[9]裴正林,董玉珊,彭苏萍.裂隙煤层弹性波场方位各向异性特征数值模拟研究.石油地球物理勘探,2007,42(6):665-672.

Pei Zhenglin,Dong Yushan,Peng Suping.Numerical simulation of azimuthal anisotropy of elastic wave field in fractured seams.OGP,2007,42(6):665-672.

[10]裴正林.层状各向异性介质中横波分裂和再分裂数值模拟.石油地球物理勘探,2006,41(1):17-25.

Pei Zhenglin.Numerical simulation of splitting and splitting of transverse wave in layered anisotropic media.OGP,2006,41(1):17-25.

[11]李东,董守华,赵小翠等.煤储层双相EDA介质的地震波场模拟.地球物理学进展,2011,26(2):654-663.

Li Dong,Dong Shouhua,Zhao Xiaocui et al.Simulation of seismic wave field in coal reservoir with dual phase EDA medium.Progress in Geophysics,2011,26(2):654-663.

[12]王宏伟,彭苏萍,杜文凤等.HTI构造煤方位AVO正演.石油地球物理勘探,2014,49(6):1122-1130.

Wang Hongwei,Peng Suping,Du Wenfeng et al.HTI structural coal orientation AVO forward.OGP,2014,49(6):1122-1130.

[13]镇晶晶,刘洋,李敏.几种裂缝模型的波场传播特征比较.石油地球物理勘探,2012,47(6):908-917.

Zhen Jingjing,Liu Yang,Li Min.Comparison of wave field characteristics among the fracture rock models.OGP,2012,47(6):908-917.

[14]Lebedev V I.Difference analogues of orthogonal decompositions,basic differential operators and some boundary problems of mathematical physics I.USSR Computational Mathematics and Mathematical Phy-sics,1964,4(3):69-92.

[15]Bernth H,Chapman C.A comparison of finite-difference grids for anisotropic elastic modeling.SEG Technical Program Expanded Abstracts,2010,29:2916-2920.

[16]Lisitsa V,Vishnevskiy D.Lebedev scheme for the numerical simulation of wave propagation in 3D anisotropic elasticity.Geophysical Prospecting,2010,58(4):619-635.

[17]林朋,彭苏萍,卢勇旭等.基于旋转交错网格的双相各向异性介质二维三分量波场模拟.煤炭学报,2016,41(5):1203-1211.

Lin Peng,Peng Suping,Lu Yongxu et al.Study on 2D/3C wave propagation in two-phase anisotropic media using the rotated staggered-grid method.Journal of China Coal Society,2010,58(4):619-635.

[18]李娜,黄建平,李振春等.Lebedev网格改进差分系数TTI介质正演模拟方法研究.地球物理学报,2014,57(1):261-269.

Li Na,Huang Jianping,Li Zhenchun et al.Research on Lebedev mesh modified differential coefficient TTI forward modeling method.Chinese Journal of Geophysics,2014,57(1):261-269.

[19]李娜,李振春,黄建平等.Lebedev网格与标准交错网格耦合机制下的复杂各向异性正演模拟.石油地球物理勘探,2014,49(1):121-131.

Li Na,Li Zhenchun,Huang Jianping et al.Complex anisotropic forward modeling based on Lebedev mesh and standard staggered mesh coupling mechanism.OGP,2014,49(1):121-131.

[20]黄建平,杨宇,李振春等.基于M-PML边界的Lebedev网格起伏地表正演模拟方法及稳定性分析.中国

石油大学学报(自然科学版),2016,40(4):47-56.

Huang Jianping,Yang Yu,Li Zhenchun et al.Forward modeling method and stability analysis of Lebedev grid based on M-PML boundary.Journal of China University of Petroleum(Edition of Natural Science),2016,40(4):47-56.

[21]杨宇,黄建平,雷建设等.Lebedev网格黏弹性介质起伏地表正演模拟.石油地球物理勘探,2016,51(4):698-706.

Yang Yu,Huang Jianping,Lei Jianshe et al.Forward modeling of viscoelastic medium in Lebedev lattice.OGP,2016,51(4):698-706.

[22]杨庆节,刘财,耿美霞等.交错网格任意阶导数有限差分格式及差分系数推导.吉林大学学报,2014,44(1):375-385.

Yang Qingjie,Liu Cai,Geng Meixia et al.Staggered grid finite difference scheme and coefficients deduction of any number of derivatives.Journal of Jilin University(Earth Science Edition),2014,44(1):375-385.

[23]王洋,刘洪,张衡等.一种全局优化的隐式交错网格有限差分算法及其在弹性波数值模拟中的应用.地球物理学报.2015,58(7):2508-2524.

Wang Yang,Liu Hong,Zhang Heng et al.A global optimized implicit staggered grid finite difference algorithm and its application in numerical simulation of elastic wave.Chinese Journal of Geophysics,2015,58(7):2508-2524.

[24]尹志恒,狄帮让,魏建新等.裂隙参数对纵波能量衰减影响的物理模型研究.石油地球物理勘探,2012,47(5):728-734.

Yin Zhiheng,Di Bangrang,Wei Jianxin et al.P-wave attenuation by fracture parameter on physical models.OGP,2012,47(5):728-734.

[25]沈金松,詹林森,马超.裂缝等效介质模型对裂缝结构和充填介质参数的适应性.吉林大学学报:地球科学版,2013,43(3):993-1003.

Shen Jinsong,Zhan Linsen,Ma Chao.The applicability of fracture effective model to diffeerent parameters of fracture geometric strutures and media filled in fracture pores.Journal of Jinlin University(Earth Science Edition),2013,43(3):993-1003.

[26]姚振岸,孙成禹,谢俊法等.黏弹TTI介质旋转交错网格微地震波场模拟.石油地球物理勘探,2017,52(2):253-263.

Yao Zhen’an,Sun Chengyu,Xie Junfa et al.Simulation of micro-seismic wave field in viscous TTI medium rotating staggered.OGP,2017,52(2):253-263.