基于等效交错网格的流固耦合介质地震波模拟

吴建鲁　吴国忱　王　伟　何　京

(①中国石油大学(华东)，山东青岛 266580； ②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071； ③中海石油(中国)有限公司天津分公司渤海石油研究院,天津塘沽 300459)

1　引言

流固耦合介质在现实世界中普遍存在，包括海洋环境、河流、坝体和船舶等。地震波在流固耦合介质中的数值模拟，一直是研究热点和难点。Hou等[1]将流固耦合介质地震波数值模拟方法分为两种： ①单一方程法，即在流相和固相中采用相同的地震波波动方程，利用一阶速度—应力方程针对流固耦合介质进行地震波数值模拟[2-7]，不必考虑界面的几何特征，实现方法简单，但是由于方程中的变量较多(各向同性条件下二维情况为5个，三维情况为9个)，计算效率相对较低； ②双方程耦合方法，即分别用声波方程和弹性波方程描述地震波在液相和固相介质中的传播，并利用连续性条件将两种介质联系起来，但需要精确考虑流固耦合介质的界面信息。Stephen[5，8]和Sochackid等[9]利用流固界面的应力、应变连续性条件采用有限差分方法对声学和弹性介质的纯位移方程耦合进行了正演模拟，虽然短时间内波场传播十分稳定，但随着传播时间的增加，界面耦合近似误差积累逐渐导致地震波传播不稳定； 另外，界面处耦合差分方法很难适用于高阶格式，极大地限制了空间差分步长的选择。Lee等[10]结合流固界面连续性条件利用单元网格有限差分数值法模拟了水平界面情况下的地震波传播，同样该方法很难推广到高阶差分格式，限制了实际应用。曲英明等[11]和Qu等[12]利用一阶速度—应力方程将该方法推广到海底起伏模型情况，克服了起伏界面模拟时的阶梯散射波场干扰。Komatitsch等[13]利用谱元法数值模拟了水平及起伏海底条件的地震波传播，模拟结果相对稳定； Carcione等[14]利用伪谱法分析了海底不同形式波的传播特征； Zhang[15]结合有限差分和有限元方法进行了单元格子法流固界面地震波数值模拟方法研究，该方法对起伏不规则海底界面适用性相对较强； 宣领宽等[16]考虑了四边形单元的双线性特性并结合变步长思想进一步提高了数值模拟精度。Choi等[17]在二阶声压波动理论和弹性位移波动理论框架下采用频率域有限元方法模拟了流固耦合介质地震波传播，Bae等[18，19]将该方法应用于不同形式下的全波形反演，进一步验证了方法的稳定性和有效性。Yu等[20，21]通过声压与应力参数的定量关系将传统的一阶速度—应力方程变换为一阶速度—应力—压力方程，并用于海上各向同性和VTI介质的逆时偏移。

上述方法中采用一阶速度—应力波动方程模拟精度相对较高且流固界面模拟稳定，但是在现有计算环境下进行实际应用时，势必会面临计算量大、计算效率相对较低的问题[17，22-24]。基于有限元、谱元和单元格子法采用双方程耦合方法可以有效地模拟流固边界处的地震波传播，但是该方法需要进行精确的网格剖分，尤其针对复杂三维情况下的剖分需要特别留意，以免引入不必要的误差[25-27]。Bartolo等[28，29]借助交错网格差分思想提出了针对二阶声压标量波方程和二阶纯位移波动方程的时间域等效交错差分正演模拟，该方法不但和一阶交错差分具有同样的差分精度，而且含有的参数变量较少，节省了大量内存，提高了正演模拟效率。本文借助等效交错网格思想并充分考虑密度参数空间变化对地震波传播的影响，在流相介质和固相介质中分别采用非均质情况二阶声压标量波、二阶纯位移控制方程，为提高地震波在流固相介质中传播的精度和稳定性，在流固耦合界面处采用一阶位移—应力弹性波动方程作为流相和固相之间的转换过渡层，并详细说明了过渡层与上、下介质进行时间和空间差分的耦合方法。利用该方法对不同模型进行测试并与一阶交错网格速度—应力方程的结果进行对比，证明了方法的准确性和稳定性。

2　流固耦合介质正演模拟方法

2.1　流固耦合介质波动方程

在各向同性非均质情况下，流体中剪切应力为零，一般用声压参数和位移矢量进行刻画，流相中的物理参数一般包括两个：模量(K)和密度(ρ)，通过一阶速度—压力方程可得非均质情况下声压标量波的波动方程

(1)

其二维形式为

(2)

式中：P为压力；K为液相的体积模量；S(x，t)为震源函数；ρ为密度。

在非均质条件下各向同性二阶纯位移波动方程为

(3)

其二维形式为

(4)

式中：u(x，t)=[U(x，z，t)，W(x，z，t)]为位移向量；λ和μ为拉梅系数；F=(fx，fz)为震源函数。

2.2　等效交错网格思想

以二维为例，如图1所示，传统的交错网格差分格式是在空间和时间上应力(τxx，τzz，τxz)和速度(vx，vz)交错更新，每次都需要保存至少两个时刻的所有参数值，而等效交错网格在利用其周围应力或应变信息时，又可以采用其本身的差分格式来代替，从而实现仅含有纯压力(应力)或纯位移交错差分思想。式(4)中x方向空间四阶、时间二阶的差分格式为

图1　传统交错和等效交错网格差分格式示意图

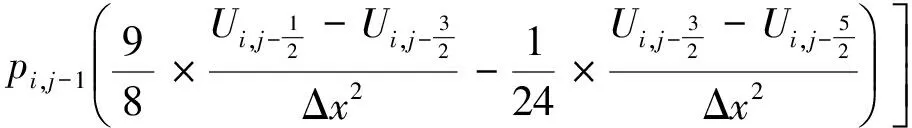
(5)

(6)

式中：Δx和Δz分别为x和z方向的网格间隔；p为介质的弹性参数或弹性参数的组合。式(2)和式(4)中的其他偏微分项的差分格式与式(5)和式(6)类似，不再赘述。

2.3　基于交错网格流固界面过渡层

借助交错网格可以稳定数值模拟地震波在流固界面传播的特点，在流固界面处采用一阶位移—应力波动方程差分模拟，与上覆流相中的声压标量波方程和下伏固相中的纯位移弹性波方程的等效交错网格格式耦合差分，如图2所示。假设流固界面为水平界面，Δt为时间间隔，NfΔz为流固界面的深度，从深度(Nf-4)Δz到(Nf+5)Δz为常规交错网格的区域。假设已知(n-1)Δt时刻从0到NfΔz之间的压力分量、从(Nf-10)Δz到(Nf+8)Δz之间的应力分量和从(Nf-6)Δz到NzΔz处位移分量(Nz为模型z方向网格数)，首先应用应力—位移关系(式(8))和弹性波位移方程(式(4))分别更新从(Nf-10)Δz到(Nf+4)Δz之间和从(Nf+5)Δz到NzΔz之间nΔt时刻的位移分量，再利用应力—位移关系式(式(8))更新从(Nf-3)Δz到(Nf+8)Δz之间nΔt时刻的应力分量，利用式(2)和压力—应力连续方程(式(7))分别更新从0到(Nf-4)Δz之间和从(Nf-3)Δz到NfΔz之间nΔt时刻的压力分量，最后利用式(7)更新(Nf-10)Δz到(Nf-4)Δz之间nΔt时刻的应力分量，从而完成nΔt时刻所有变量的更新工作。利用上述流程可完成所有时刻的变量计算工作，进而完成正演模拟工作。

(7)

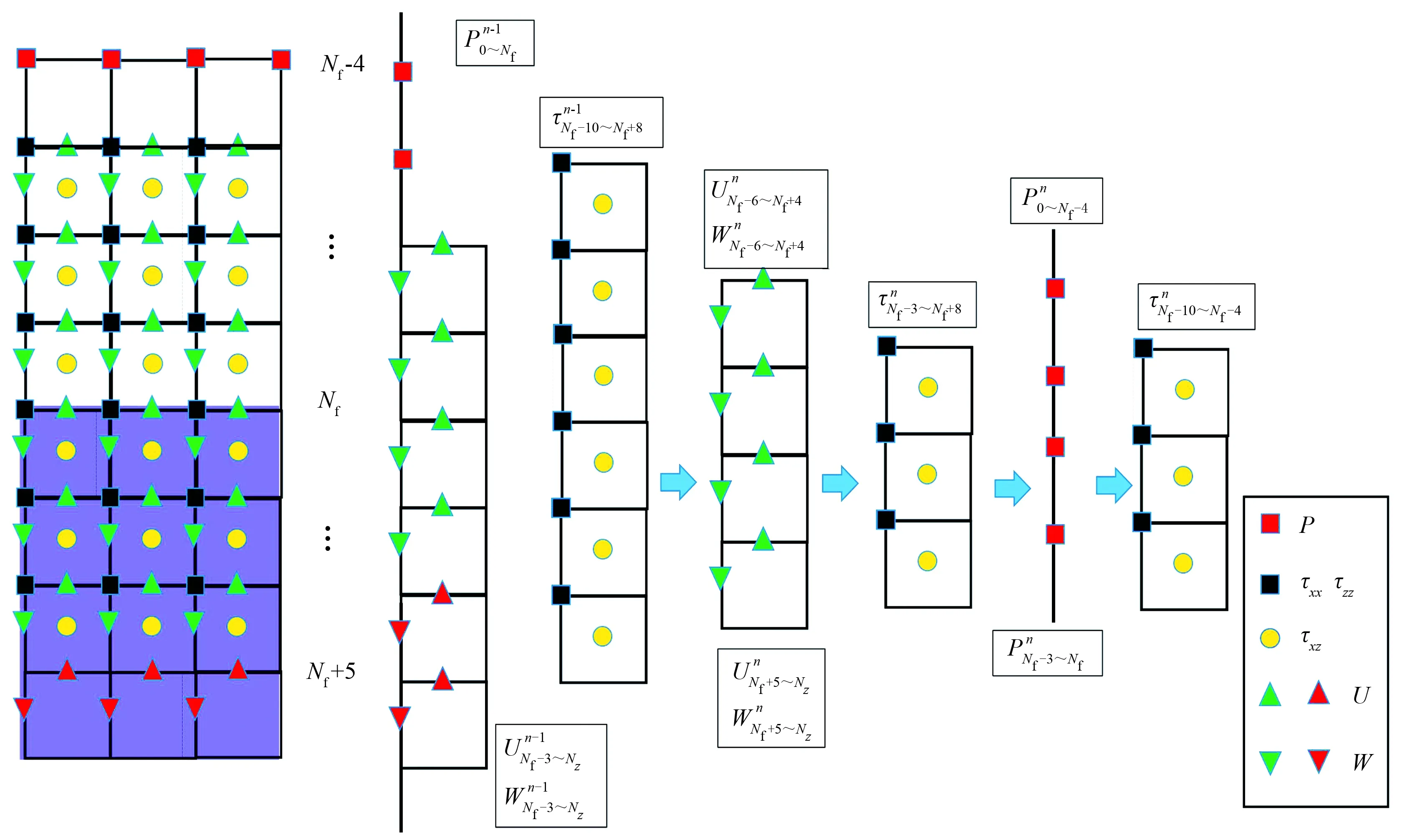
图2　基于交错网格过渡层与上、下等效交错网格耦合过程示意图

(8)

流固界面处的常规交错网格和上、下等效交错网格之间的衔接部分同样采用交错网格差分格式，实现了模型整个区域都采用交错网格差分思想，一方面保证了地震波在流、固相之间传播的稳定性，同时也保证了数值模拟的精度。本文在流相和固相中采用二阶常规PML吸收边界条件，在过渡层中采用一阶常规PML吸收边界条件。本文方法可以推广到更高阶的差分格式。

3　数值模拟结果

3.1　流固双层模型

首先，通过流固双层模型数值模拟验证本文正演方法的优势。图3为流固双层速度模型示意图，五角星代表炮点位置，距离水面60m，三角形代表声压分量接收点位置，距离水面120m。另外在海底接收水平和垂直位移分量，x与z方向的网格间隔均为6m，选用主频为20Hz的雷克子波激发，时间采样间隔为0.2ms，记录时间为1.2s。表1为本文等效交错网格(ESG)方法与传统交错网格差分(SSG)方法运行内存和计算时间的对比，可见ESG方法极大地降低了正演模拟的内存需求，约为SSG方法的三分之一。另一方面，由于耦合情况下的ESG方法只需在液相和固相中分别使用纯声压和位移弹性波动方程，提高了计算效率，ESG方法相比于SSG方法运行时间缩短了四分之一。

表1　两种方法内存及运行时间对比

同时为验证本文等效交错方法(ESG)数值模拟的准确性，对图3中的模型进行细网格剖分以便求取更为精确的数值模拟结果(可近似为解析解)，空间网格间距为1m， 时间间隔为0.05ms， 模型大小和炮点信息不变。图4为粗、细网格模拟的声压分量、水平位移及垂直位移记录对比，两种网格获得的模拟结果基本相同。为进一步研究两种方法模拟结果的波形一致性，抽取x方向900m处的单道进行比较(图5)。由于正演模拟中不可避免的空间频散和时间频散造成了二者振幅和相位的细微差异，但在误差允许的范围之内，说明了等效交错网格方法的准确性。图6为等效交错方法模拟的0.5s时刻流固双层模型的波场快照，液相为压力波场，固相为位移波场。流相和固相中的反射、透射波以及首波的模拟结果十分清晰，从另一个方面也说明了本文针对流固耦合介质地震波数值模拟方法的准确性。

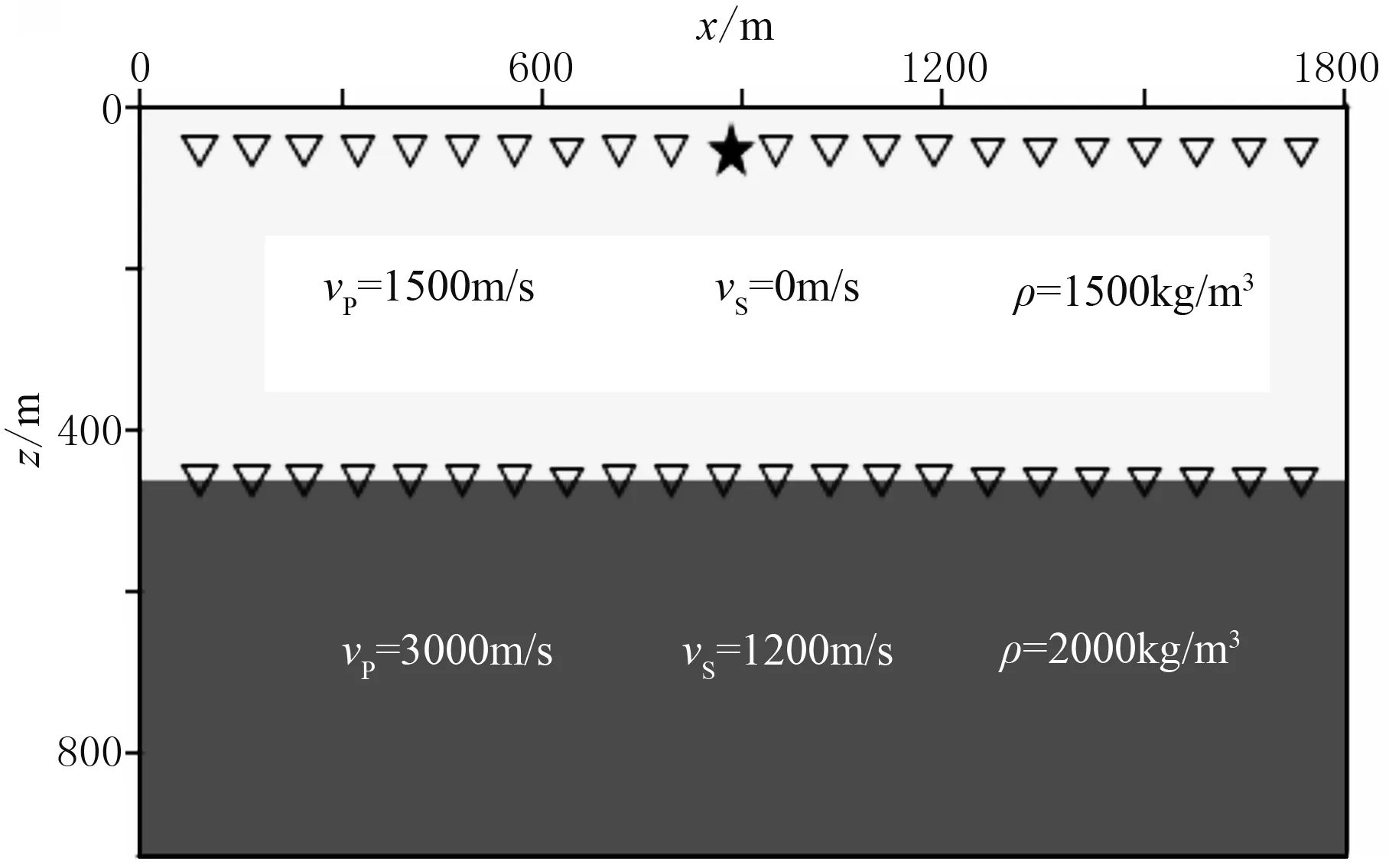
图3　流固双层模型

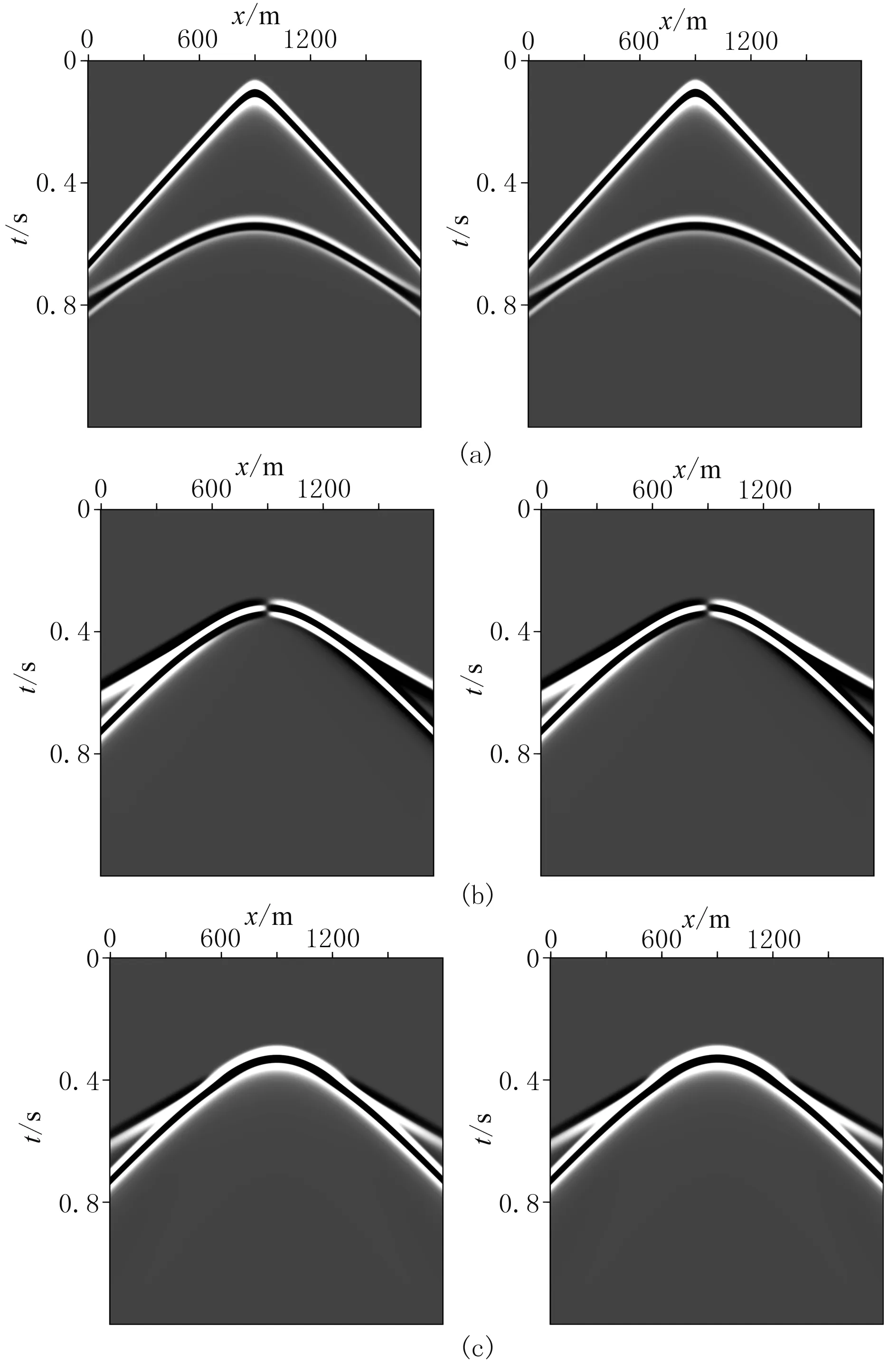
图4　　　　双层模型6m(左)和1m(右)网格间距ESG方法模拟结果对比

图5　　　　双层模型6m(黑色)和1m(红色)网格间距ESG方法模拟的x方向900m处地震记录

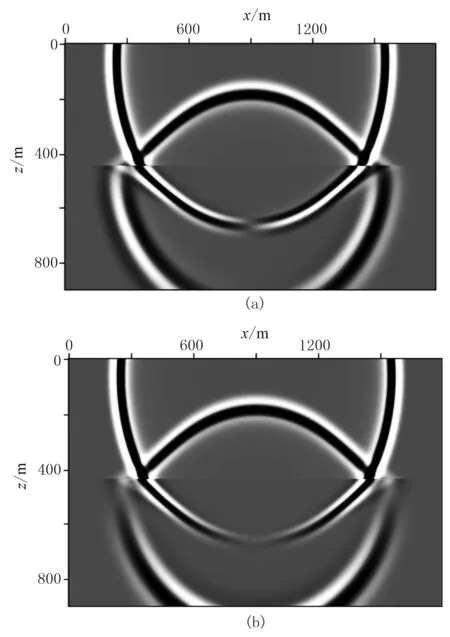
图6　双层模型ESG方法模拟的0.5s波场快照

3.2　Marmousi 2模型

为进一步验证和说明本文方法对复杂模型的适用性和稳定性，采用复杂的Marmousi 2模型(图7)进行测试。需要特别指出的是，为保证模型的模拟精度，本文未考虑原始模型中海底松软低速层的影响。模型网格数为2401×1201，两个方向的网格间距均为5m，水层的厚度为900m，在水面下50m激发主频为20Hz的雷克子波，检波器的设置在水下60m。图8为炮点位于x=6000m处利用等效交错网格(ESG)和传统交错网格(SSG)方法模拟的地震记录，两种方法都采用时间二阶和空间四阶差分格式。图9为检波器位于x=5000m处单道记录的对比，可以发现，两种方法模拟的地震信号基本一致。图10为Marmousi 2模型2.0s时刻的波场快照，可见本文提出的流固介质等效交错网格方法在复杂模型中对变速构造的模拟结果稳定，且与传统交错网格方法的空间精度相同。

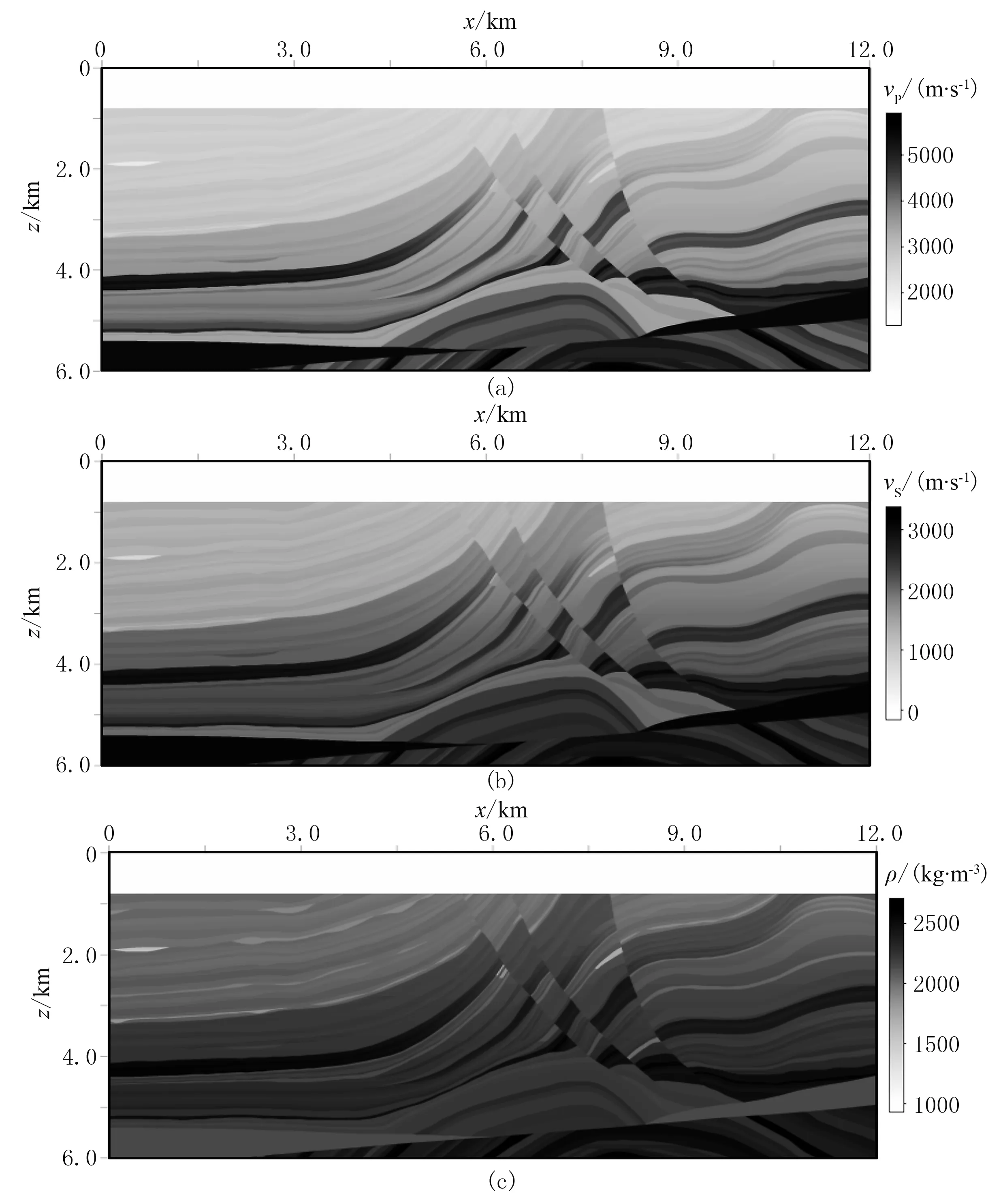
图7　Marmousi 2模型

图8　ESG方法(a)和SSG方法(b)模拟的Marmousi 2模型单炮记录

图9　　　　ESG方法和SSG方法模拟的Marmousi 2模型单道记录(a)及其局部放大(b)

图10　Marmousi 2模型ESG方法模拟的2.0s波场快照

4　分析与结论

本文借助等效交错网格的思想，给出了流固耦合介质正演模拟方法，流相介质由声压标量波方程控制，固相介质由二阶纯位移弹性波方程控制，在流固界面附近采用传统的一阶位移—应力交错网格作为过渡层，从而实现流固介质地震波正演模拟。

(1)与传统的交错网格正演模拟相比，本文提出的流固耦合介质正演模拟在保持与传统交错网格方法相同模拟精度的前提下，尽可能地减少了正演过程中的变量，降低了内存需求，提高了计算效率。

(2)通过简单流固双层模型和复杂Marmousi 2模型试算，不仅验证了等效交错网格和传统交错网格具有相同的模拟精度，而且说明了本文所述方法的准确性和稳定性。

(3)该方法同样可以推广到三维情况下，并且相对于传统的交错网格有限差分方法，本文的流固耦合地震波数值模拟方法对于海上的地震偏移和全波形反演等的研究和应用有较好的适用性。

(4)当海底界面为非水平时，则必须增加过渡层的层数，使得海底界面在过渡层之内即可。

[1]Hou G，Wang J and Layton A.Numerical methods for f-structure interaction — a review.Computer Physics Communications，2012，12(2):337-377.

[2]Virieux J.P-SV wave propagation in heterogeneous media：Velocity-stress finite-difference method.Geophysics，1986，51(4):889-901.

[3]Burns D R and Stephen R A.Three-dimensional numerical modeling of geoacoustic scattering from seafloor topography.The Journal of the Acoustical Society of America，1990，88(5)：2338-2345.

[4]Dougherty M E and Stephen R A.Seismo/acoustic propagation through rough seafloors.The Journal of the Acoustical Society of America，1991，90(5):2637-2651.

[5]Stephen R A.A review of finite difference methods for seismo-acoustics problems at the seafloor.Reviews of Geophysics，1988，26(3)：445-458.

[6]Van Vossen R，Robertsson J and Chapman C.Finite-difference modeling of wave propagation in a f-solid configuration.Geophysics，2002，67(2)：618-624.

[7]De Basabe J D and Sen M K.A comparison of finite-difference and spectral-element methods for elastic wave propagation in media with a f-solid interface.Geophysical Journal International，2015，200(1)：278-298.

[8]Stephen R A.A comparison of finite difference and reflectivity seismograms for marine models.Geophy-sical Journal International，1983，72(1)：39-57.

[9]Sochacki J S.Interface conditions for acoustic and elastic wave propagation.Geophysics，1991，56(2)：168-181.

[10]Lee H，Lim S and Min D.2D time-domain acoustic-elastic coupled modeling：a cell-based finite-difference method.Geosciences Journal，2010，13(4):407-414.

[11]曲英铭，黄建平，李振春等.基于单元交错网格的变坐标系正演模拟方法在声—弹介质中的应用.石油物探，2015，54(5)：582-591.

Qu Yingming，Huang Jianping and Li Zhenchun et al.The application of variable coordinate system forward modeling using cell-based staggered grids in acoustic-elastic coupled medium.GPP，2015，54(5)：582-591.

[12]Qu Y，Huang J and Li Z et al.A hybrid grid method in an auxiliary coordinate system for irregular f-solid interface modeling.Geophysical Journal International，2017，208(3)：1540-1556.

[13]Komatitsch D，Barnes C and Tromp J.Wave propagation near a fluid-solid interface：A spectral-element approach.Geophysics，2000，65(2):623-631.

[14]Carcione J M and Helle H B.The physics and simulation of wave propagation at the ocean bottom.Geophysics，2004，69(3)：825-839.

[15]Zhang J.Wave propagation across f-solid interfaces：a grid method approach.Geophysical Journal International，2004，159(1)：240-252.

[16]宣领宽，张文平，明平剑等.基于不同时间步长时域非结构有限体积法模拟声—弹性耦合问题.固体力学学报，2013，34(2)：158-168.

Xuan Lingkuan，Zhang Wenping and Ming Pingjian et al.Numerical simulation of acoustic-elastic interaction based on muti-time-step unstructured finite volume time domain method.Chinese Journal of Solid Mechanics.2013，34(2)：158-168.

[17]Choi Y，Min D J and Shin C.Two-dimensional waveform inversion of multi-component data in acoustic-elastic coupled media.Geophysical Prospecting，2008，56(6)：863-881.

[18]Bae H S，Shin C and Cha Y et al.2D acoustic-elastic coupled waveform inversion in the Laplace domain.Geophysical Prospecting，2010，58(6)：997-1010.

[19]Bae H S，Pyun S and Chuang W et al.Frequency-domain acoustic-elastic coupled waveform inversion using the Gauss-Newton conjugate gradient method.Geophysical Prospecting，2011，60(3)：413-432.

[20]Yu P，Geng J and Li X et al.Acoustic-elastic coupled equation for ocean bottom seismic data elastic reverse time migration.Geophysics，2016，81(5)：S333-S345.

[21]Yu P，Geng J and Li X et al.Separating quasi-P-wave in transversely isotropic media with a vertical symmetry axis by synthesized pressure applied to ocean-bottom seismic data elastic reverse time migration.Geophysics，2016，81(6)：C295-C307.

[22]黄金强，李振春和黄建平等.TTI介质Lebedev网格高阶有限差分正演模拟及波型分离.石油地球物理勘探，2017，52(5)：915-927.

Huang Jinqiang，Li Zhenchun and Huang Jianping et al.Lebedev grid high-order finite-difference modeling and elastic wave-mode separation for TTI media.OGP，2017，52(5)：915-927.

[23]高正辉，孙建国，孙章庆等.基于完全匹配层构建新方法的2.5维声波近似方程数值模拟.石油地球物理勘探，2016，51(6)：1128-1133.

Gao Zhenghui，Sun Jianguo and Sun Zhangqing et al.2.5D acoustic approximate equation numerical simulation with a new construction method of the perfectly matched layer.OGP，2016，51(6)：1128-1133.

[24]梁文全，王彦飞，杨长春.声波方程数值模拟矩形网格有限差分系数确定法.石油地球物理勘探，2017，52(1)：56-62.

Liang Wenquan，Wang Yanfei and Yang Changchun.Acoustic wave equation modeling with rectangle grid finite difference operator and its linear time space domain solution.OGP，2017，52(1)：56-62.

[25]Xu K and McMechan G.2D frequency-domain elastic full-waveform inversion using time-domain modeling and a multi step-length gradient approach.Geophy-sics，2014，79(2)：R41-R53.

[26]赵慧，刘颖，李予国.自适应有限元海洋大地电磁场二维正演模拟.石油地球物理勘探，2014，49(3)：578-585.

Zhao Hui，Liu Ying and Li Yuguo.Adaptive finite element forward modeling for two-dimensional marine magnetotelluric fields.OGP，2014，49(3)：578-585.

[27]黄一凡，胡祥云，韩波.自适应有限元法的大地电磁二维各向异性正反演.石油地球物理勘探，2016，51(4)：809-820.

Huang Yifan，Hu Xiangyun and Han Bo.Forward and inverse modeling of the magnetotelluric field in 2D anisotropic media with an adaptive finite element method.OGP，2016，51(4)：809-820.

[28]Bartolo L D，Dors C and Mansur W.A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation.Geophysics,2012,77(5)：T187-T199.

[29]Bartolo L D，Dors C and Mansur W.Theory of equi-valent staggered-grid schemes：application to rotated and standard grids in anisotropic media.Geophysical Prospecting，2015，63(5)：1097-1125.