基于FPGA的AES算法中行位移与列混淆混合设计
2018-04-09彭关礼肖顺文
彭关礼,肖顺文
(西华师范大学 电子信息工程学院,四川 南充 637009)
0 引言
随着信息技术与互联网的发展,数据传送的安全性也变得越来越重要[1]。高级加密标准AES(Advanced Encryption Standard) 算法作为目前最流行的加密算法之一,无论是在商业、工业还是在军事方面都被广泛应用[2]。该加密算法是继数据加密标准DES(Date Encryption Standard)之后的新一代加密算法,采用了Rijndeal算法设计,该算法具有模块性、高效性、对称性等自身结构特点。
高级加密标准AES算法硬件实现相比软件实现提供了更好的物理安全性和更快的处理速度,FPGA(Field-Programmable Gate Array)以其可编程性为该算法的实现提供了较好的平台[3]。本文针对该算法中行位移变换模块和列混淆变换模块的特点将两个模块综合为一个整体模块基于硬件描述语言VHDL(Very-High-Speed Integrated Circuit Hardware Description Language)来实现,为AES算法中行位移与列混淆的实现提供一种可行的设计方案。
1 AES的轮函数分析
轮变换函数包括了字节替代变换(SubBytes)、行位移变换(ShfitRows)、列混淆变换(MixColumns)(除最后一轮加密外)以及轮密钥加(AddRoundKey)四个步骤的操作[4]。在AES加密算法中明文分组长度为128位固定值,而密钥分组长度的不同决定了加密的轮数和轮变换的轮数,当密钥分组长度为128位时加密轮数和轮变换轮数为10轮;当密钥分组长度为192位时加密轮数和轮变换轮数为12轮;当密钥分组长度为256位时加密轮数和轮变换轮数为14轮。虽然相应的加密轮数能够实现对数据信息进行有效地保护,但轮函数中的行位变换和列混淆变换为加密算法提供了更高的扩散性以抗击密码攻击,因此轮变换中的行位变换和列混淆变换对实现AES加密算法有着至关重要的作用。
1.1 行位移变换
行位移变换是一个简单的字节换位操作,它是将状态中的行按照不同的偏移量进行循环移位。AES加密算法中明文分组长度为固定值128位,可以抽象地用4行4列的状态矩阵来表示,每行由4字节组成。在AES加密算法中行位移变换是将第1行字向左循环移动0字节,第2行字向左循环移动1字节,第3行字向左循环移动2字节,第4行字向左循环移动3字节。
1.2 列混淆变换
列混淆变换是一个作用在4字节列上的砖匠变换,可以将每列看作是一个多项式与一个固定的多项d(x)=03.x3+01.x2+01.x+02相乘后取模x4+1,亦可用式(1)所示的矩阵形式[5]表示。
(1)
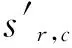
传统的AES算法轮函数中行位移与列混淆是作为单独的两个模块分别来实现,因此模块与模块之间存在线路的传输延迟以及资源的多余损耗,不利于提高该算法实现的效率以及资源空间的节省,因此文中采用了行位移与列混淆的混合设计模式。
2 行位移与列混淆的混合及算法设计
首先轮函数中的行位移变换与列混淆变换都是针对字节的变换操作,其次两者的变换都具有一定的线性性质。在原AES加密算法中行位移变换与列混淆变换是两个独立变换,因此原算法基于FPGA的硬件描述语言VHDL来实现需要两个独立模块,通过对算法中的行位移与列混淆的分析可以将它们综合为一个整体模块来实现。
2.1混合设计

(2)
其中{X}H表示十六进制数,⊕表示异或运算,X取01,02,03,i取0,4,8,12。为了更好地实现混合设计,式(2)中乘02、乘03统一定义为Xtime()[6]运算,设a=b7b6b5b4b3b2b1b0(a表示十六进制数,其中b7,b6,b5,b4,b3,b2,b1,b0表示依次从高位到低位的二进数)。定义Xtime()按照以下方式运算,如式(3)所示,c=00011011是用二进制数表示的常量。
(3)
因此由式(2)经过变换整理可以得到式(4)。
(4)
从理论角度而言整合设计模块优于原算法中两个独立模块,整合后的模块省去了一些中间变换步骤,同时也能够消除模块之间传输的线路延迟,但效率的提升因软件、硬件以及加密时的文件大小不同而有所差异[7]。
2.2 混合设计的FPGA实现
硬件描述语言VHDL具有功能强大、设计灵活、与具体器件无关等自身结构优点[8],而AES加密算法基于硬件实现优于软件实现。因此采用专有硬件来实现AES加密算法更能显示其中的优点。实现行位移与列混淆变换的部分VHDL程序如下:
library ieee;
use ieee.std_logic_arith.all;
use ieee.std_logic_1164.all;
use ieee.std_logic_unsigned.all;
.
.
s0:=Xtime(h1,(e0 xor e5)) xor (e5 xor e10) xor e15;
s1:=Xtime(h1,(e5 xor e10)) xor (e10 xor e15) xor e0;
s2:=Xtime(h1,(e10 xor e15)) xor (e0 xor e15) xor e5;
s3:=Xtime(h1,(e0 xor e15)) xor (e0 xor e5) xor e10;
3 实验仿真
基于Quartus II 9.1 (32-Bit)版本,在cyclone iii系列下的EP3C80F484C8芯片上进行了实验仿真,其中资源利用率如图1所示,基于芯片EP3C80F484C8中的81264个LE资源(Total logic elements)仅使用216个,占用率小于1%,引脚数(Total pins)利用率为87%。

FamilyCycloneIIIDeviceEP3C80F484C8TimingModelsH/ATotallogicelements216/81,264(<1%) Totalcombinationalfunctions216/81,264(<1%) Dedicatedlogicregisters128/81,264(<1%)Totalregisters128Totalpins257/296(87%)Totalvirtualpins0Totalmemorybits0/2,810,880(0%)EmbeddedMultiplier9-bitelements0/488(0%)TotalPLLs0/4(0%)
图1资源利用率
为了验证该混合设计模块的稳定性和可靠性,分别给出了不同工作频率下不同输入数据对应的输出数据结果,具体测试结果如表1所示。

表1 相关数据测试
由表1可知,在工作频率分别为1 000MHz和100MHz时,当输入数据din=DEE570E3749B9BBA7516C67
69D51924D,对应的数据输出为dout=52C192121EF7DCDBC580F2222DDFB28E,其吞吐率分别可以达到9.78Gb/s和7.28Gb/s.当输入数据din=22C93CBFD2C73A6B1418407FB88D214A,对应的数据输出为dout=5CC307CC246A8B0B191FF3C11DF9BAB1,其吞吐率分别可以达到9.30Gb/s和7.21Gb/s.
测试使用的时钟频率为1000MHz时,第1组数据的仿真结果如图2所示:

测试使用的时钟频率为100MHz时,第1组数据的仿真结果如图3所示:

测试使用的时钟频率为1 000MHz时,第2组数据的仿真结果如图4所示:

测试使用的时钟频率为100MHz时,第2组数据的仿真结果如图5所示:

4 总 结
本文通过对原AES算法中的行位移变换与列混淆变换的分析,针对这两种变换的特点经过整合来实现两个模块所能单独实现的功能,实验仿真结果表明基于FPGA的硬件描述语言VHDL实现AES算法的行位移与列混淆的混合设计是可行的,在不同的工作频率下达到了数据的不同处理速度,在同一工作频率下不同输入数据达到了相应的工作频率。
参考文献:
[1]肖振久,胡驰,姜正涛,等.AES与RSA算法优化其混合加密体制[J].计算机应用研究,2014,31(4):1189-1198.
[2]于松林,王文工,陈博,等.基于FPGA的AES硬件实现及优化[J].电子设计工程,2017,25(6):75-83.
[3]张伟,高俊雄,王耕波,等.一种优化的AES算法及其FPGA实现[J].计算机与数字工程,2017,45(3):502-505.
[4]赵跃华,马林林.AES算法的轻量化实现研究[J].计算机工程与应用.2015,51(6):79-83.
[5]赵哲斐.AES算法IP核优化与设计[D].西安:西安电子科技大学,2013.
[6]王颖.高级加密标准AES中MixColumns()函数的改进[D].西安:陕西师范大学,2011.
[7]刘秀莲.AES算法的一种快速实现方法[J].计算机安全,2012(06):47-49.
[8]朱松柏,肖顺文,江敏.基于FPGA的AES解密算法研究[J].成都工业学院学报,2016,19(2):27-30.
