基于ANSYS断路器触头微间隙发热产生机理的仿真研究
2018-04-09王晓娟
周 颖,李 想,王晓娟
(三峡大学 电气与新能源学院, 湖北 宜昌 443002)
0 引 言
开关设备是电力系统中的常用器件,由于接触电阻的存在,其触头/接头间在电路导通时会出现温升。目前对于电接触的发热原因已经有了很深入的研究,但对于温升引起的触头间的塑性形变的研究较为缺乏。当断路器温升很高时,由于热胀冷缩效应,热胀后的触头/接头将紧紧地接触;温升再高时,触头/接头材料开始软化,软化后的触头/接头在热应力的作用下,将出现不可逆的塑性形变,温降后形变不能复原,触头间就出现了微间隙。
1 电接触模型
电接触的分类大体分成面-面接触、点-点接触和线-线接触,在实际中使用最多的是面-面接触,如图1所示。在电力系统中使用的接触材料更多的是铜和铝,虽然银金属的导电性能比铜和铝的好很多,但是由于银是贵金属,一般只作为电接触表面的金属镀层来存在,这样在使用尽量少的贵重金属的情况下使电接触的性能提高很多。
2 电接触形变理论分析
无论进行哪种热分析,都会在接触实体中存在热传导,就要遵循热力学的热传导方程:
式中:ρ为接触材料的密度;c为接触材料的比热容;T为温度,它是空间坐标(x,y,z)和时间t的函数;kxx为接触体材料的热传导系数,一般情况下热传导系数是常数,但有些情况下它是空间坐标和时间的函数;Sh为单位体积内的生热率,如果没有的话则为0。

图1 电接触现象
接触界面上的热流密度可以根据给出的接触界面的参数来求解:
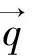
在电接触理论方面,目前有两种说法最为流行,第一种,表述温度关系与接触电压降之间的联系,即
U1/4A=T2m-T20
式中,U1为接触电压降。
其二是R.Holom提出来的集中电阻理论,即
R1=ρ/ 2a
式中,R1为集中电阻;a为接触半径。在1932年,嚯穆对这一理论在验证时使用了纯净的铂触头,最终得出结果的误差范围为±1.5%,目前这个理论被广泛采用。但与电压—温度理论不同,这里我们假定一个常量为接触区的温度[2]。本文的研究建立在Holm的研究基础上。由于嚯穆的集中电阻理论假定了:接触面上没有表面层的存在, 两接触元件的材料、几何形状尺寸完全相同或对称,电流线收缩区的温度不变,且仅考虑其稳定状态[2]。
取参量的边界条件,当μ=0,t=Tm;当μ→时t=T0。有
如果加在触头上的压力为P,触头材料的压缩或流动极限为σ,则有
P/πa2=σ
将上式合并则有
3 实例分析
目前有两种方法用于ANSYS热结构耦合分析:直接耦合法和顺序耦合法。本文采用ANSYS顺序耦合分析方法。第一步,热分析求得结构的温度场;第二步,初始载荷为温度场,配合其他结构载荷进行热结构分析,求得结构的应力、应变分布。以上耦合过程的仿真流程如图2所示。
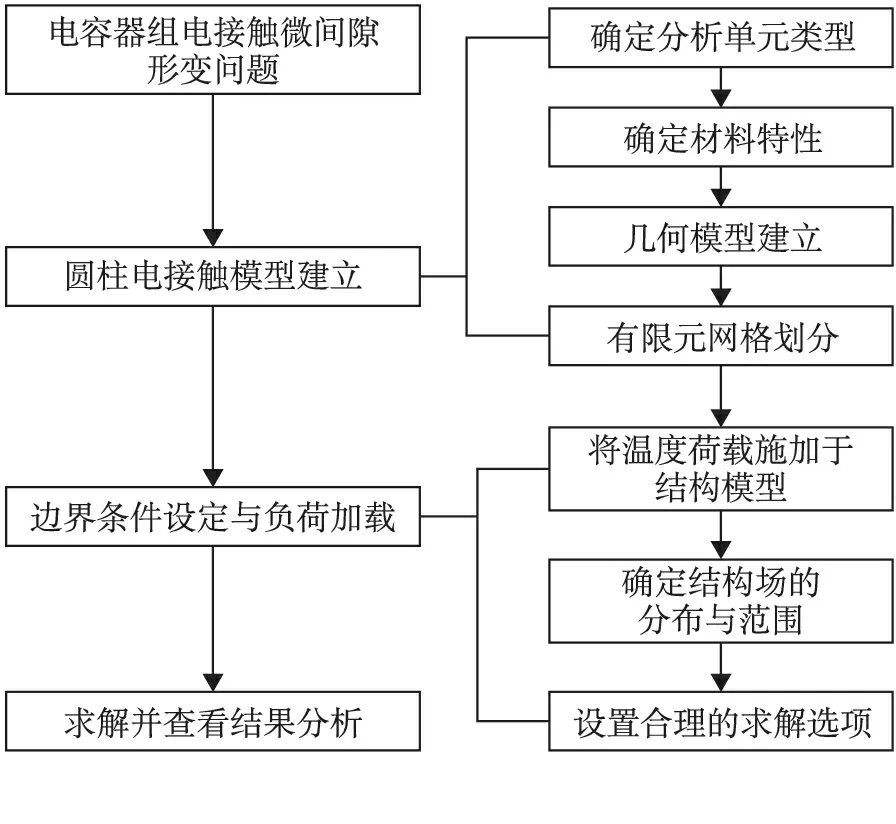
图2 ANSYS仿真流程图
根据图2的流程,对断路器触头的接触电阻进行稳态热分析,大致可以分三部分:(1)建立模型;(2)加载求解;(3)查看分析结果。其中,建立模型分为如下步骤:①完成必要的热处理;②将结构分析作为分析类型;③进行单元转换,将ANSYS热分析单元转变为结构分析单元;④定义材料附加性能参数,如弹性模量、热传导系数、热膨胀系数、泊松比等;⑤将温度载荷施加于结构模型,选择前面热分析生成的ANSYS结果文件主轴作为结构分析的热载荷加到节点上;⑥定义结构分析选项并求解;⑦结果后处理[3-4]。
3.1 模型建立
首先按照实际断路器触头接触的圆柱型模型的尺寸进行一定比例的放大,建立两个半径为1 m、长为1 m的圆柱相接触。
其次,根据触头的形状和特性,选取耦合场六面体实体单元SOLID173进行计算,根据表1设定的仿真模型材料参数,进行铜-铜接触的研究。

表1 材料特性
通过ANSYS内部单元及参数设定,建立球型接触模型。最后,根据计算的精度要求,设置网格划分密度为0.1,完成网格划分后的模型如图3所示。
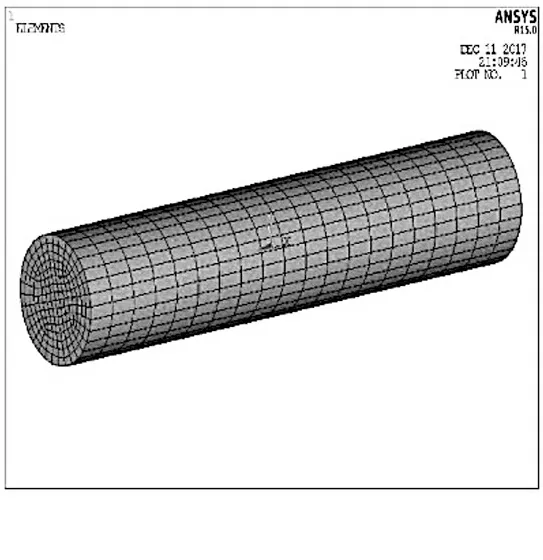
图3 电接触模型网格划分
3.2 边界条件与载荷设定
在实际的电厂或变电站中,断路器触头的接触电阻尺寸往往只有几微米,同时通过的电流也很小。为了在使用ANSYS软件时方便网格划分与计算,同时又具有实际研究价值,在本文的研究中,将电阻大小与电流大小按照一定比例放大,最终选取两个半径为1 m的圆柱体相接触,接触面的温度为800°,其他表面的温度为室温20°。
导热是固体-流体的边界上最基本的能量交换方式,将这些能量带走的方式是流体的对流。因此根据流体流动方式不同,对流换热主要分成强迫对流换热和自然对流换热[5]。采用自然条件下的对流换热后,结果如图4所示。
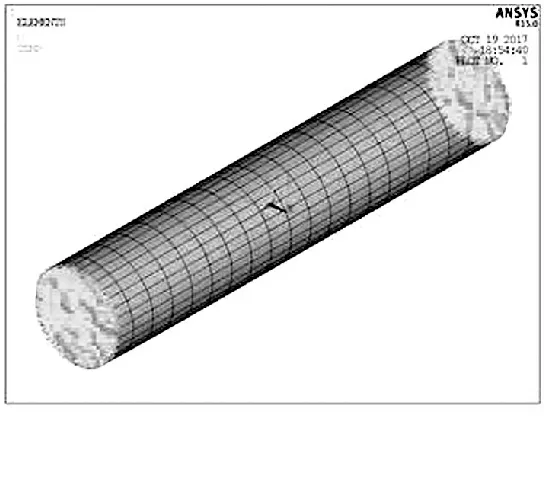
图4 电接触模型载荷加载图
3.3 ANSYS触头模型稳态结果处理
求解完毕后,查看通用后处理(General Postproc)可以得到铜制材料触头的温度分布如图5所示,得到的位移图如图6所示。

图5 触头材料分布图
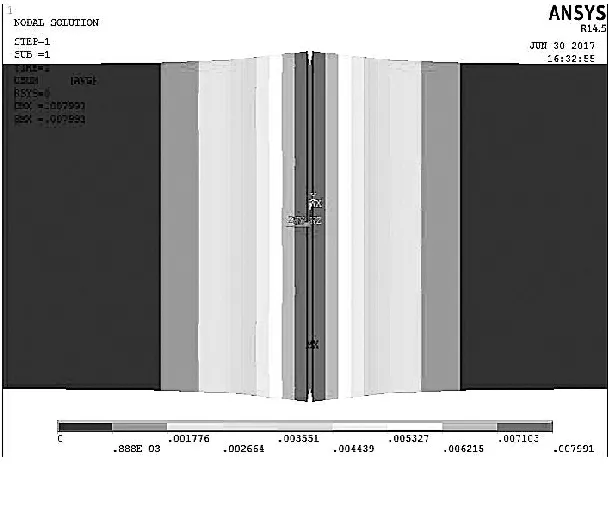
图6 触头材料位移图
由图5可知,触头接触面的温度最高,可达800℃。随着温度的升高,铜的硬度也在发生变化,在800℃的高温下铜已经开始软化,由于热膨胀力触头间发生挤压,在接触面处产生明显的形变。由图6明显可看出形变主要沿半径方向发生。
4 结 论
通过例子分析可清晰得出,目前,用 ANSYS 仿真软件可以直观看出触头系统电接触时的温度场分布以及应变结果,得出电流产生的焦耳热会使触头材料发生硬度上的改变致使触头形状发生变化,从而估计若温度再升高触头可能发生的熔焊现象,对保证继电器可靠工作的性能具有重要作用。
参考文献:
[1]Wilson C, McIntosh G, Roland S Timsit. Contact Spot Temperature and the Temperature of External Surfaces in an Electrical Connection[J]. International Conference on Electrical Contacts, 2012, 259(3):12-17.
[2]王白眉. 论触头接触压力与温升关系的计算公式[J]. 高压电器, 1982,(4):48-51.
[3]李兴山, 王爱良. 基于ANSYS的电主轴热结构耦合分析[J]. 成组技术与生产现代化, 2013, 30(4):5-7.
[4]李兴山, 王爱良. 镗铣加工中心电主轴耦合温度场的分析与研究[J]. 机床与液压, 2014,(11):19-22.
[5]李想, 张琦, 王晓娟,等. 基于ANSYS电气设备接头的电热耦合场分析[J]. 电工电气, 2017,(10):34-37.
[6]任晓霞. ANSYS在低压电器触头电接触稳态热分析中的应用[J]. 电气技术, 2008,(12):83-85.
