变压器局部放电定位方程组求根公式解算方法
2018-04-10周广方汪伟斌
周广方,汪伟斌
(1.浙江群力电气有限公司,浙江 杭州 310000;2.杭州凯达电力建设有限公司,浙江 杭州 310000)
0 引 言
电力变压器是电力系统中关键的设备,它承担着电压变换、电能分配以及电能传输的重要任务。一旦变压器发生故障,可能会导致大范围的停电,并由此造成重大的经济损失。电力变压器的正常运行对电力系统运行的可靠性有非常重要的意义。由于在运行中的电力变压器承受着高压,并且其内部场强分布不均,可能让场强高的某些地方先发生放电。局部放电对绝缘将会产生巨大危害[1-3],主要表现:带电粒子对绝缘材料的撞击,破坏其分子结构;局部放电产生局部高温,导致绝缘劣化加快;局部放电会产生一系列化学物,如O3、NO、NO2等物质,这些生成物遇水将生成硝酸,腐蚀绝缘;局放产生的辐射将会使绝缘材料分解;局放产生的气体将导致局部压强增大,挤压绝缘介质。
局部放电将导致绝缘劣化,最终导致绝缘击穿,引发电力事故。因而对局部放电的检测识别具有很重要的意义。研究还表明,变压器绝缘的劣化程度不仅与局放的类型、放电量、放电重复率等有关,还与放电的位置有关[4]。局放的定位能够判断绝缘损坏的严重程度以及制定有针对性的检修策略,缩短变压器的检修时间,进而提高系统的可靠性[5]。如果仅靠局部放电的检测,还是难以全面了解设备内部的绝缘状况,必须找出局放源的准确位置,将检测信息和定位结果综合起来,快速掌握内部的绝缘缺陷严重程度,并且及早地排除故障。
1 变压器局部放电定位基本模型
本文使用双曲面定位法。双曲面定位法是以其中一个传感器为参考传感器求出各个传感器相对于参考传感器的声波到达时间差来建立方程的。对于三维定位,这种方法至少需要4个方程和4个传感器,因为未知量有PD源的坐标(x,y,z)和声波到达参考传感器的时间T。这种定位方法精度较高,定位速度快,简单易行,较有发展前景。实际操作中,定位误差不可避免。误差的主要来源有:背景噪声对时延估计的影响、传感器性能、声波的速度测量误差、传感器的位置测量误差、声波的传播路径的影响和定位算法本身的缺陷。

图1 局部放电定位基本模型
局部放电的故障定位模型如图1所示。S1、S2、S3、S4、Sn分别表示超声波传感器,假设以S1为参考传感器。当局部放电发生时,其到达各个传感器的时间分别为t1、t2、t3、t4、tn,其中t1为T。各个传感器的坐标依次为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4)、(xn,yn,zn)。PD源的坐标为(x,y,z)。假设声波在介质中的传播速度一定,为v。则根据勾股定理,有如下等式:
(1)
式中,下标i表示第i个传感器,d表示传感器到PD源的位置。传感器不能测量出声波的传播时间,只能测出声波的到达时间差,时间差的定义表示如下:
τi1=ti-t1
(2)
将距离用时间差表示出来:
di=v(τi1+T)
(3)
根据以上三个式子,假设采用4个传感器,可以得出变压器局部放电故障定位方程如下:
(4)
方程组(4)的未知量有x,y,z和T。从方程可以看出,主要影响定位精度的是能否准确测量出时差、传感器位置和声波的传播速度。该方程组由4个双曲面方程组成,4个双曲面在空间中相交可以确定出2个点,通过排除法可以得到一个确定的点。
2 定位方程组求根公式解算方法
将式(4)方程组中的第2、3、4个方程分别与第一个方程相减,可得:
(5)
式中有:
(6)
上式表示各个传感器到坐标原点的距离平方。可以把式(5)写成矩阵形式:
AX=BD+C
(7)
其中有:
(8)

(9)
(10)
(11)
D=[T]
(12)
在式(7)两端乘A的逆矩阵,可得:
X=A-1BD+A-1C
(13)
令F=A-1B,H=A-1C,F与H均为三行一列的矩阵。则有:
X=FD+H
(14)
(15)
式(15)是将PD源的坐标表示成基准时间T的函数,将式(15)代入式(4)中的第一个方程,可得:
(16)
记K=[x1,y1,z1],则式(16)可以改成下面的矩阵形式:
(FTF-v2)T2+2(FTH-FTKT)T
+(HTH+KKT-2KH)=0
(17)
上式是关于基准时间T的一元二次方程,可以根据求根公式将方程的解直接求出。令L=FTF-v2,M=2(FTH-FTKT)N=HTH+KKT-2KH,得:
(18)
将式(18)代入式(15)中,可得PD源的坐标。再根据得到的PD源坐标进行计算校对,与测量出的时差比较,排除一个解。
3 算例分析
变压器的实际尺寸为长2 300 mm,宽1 800 mm,高2 400 mm。仿真时各个传感器的触头坐标取值如下:x2=1 150;y2=0;z2=800;x3=1 450;y3=0;z3=1 600;x4=850;y4=0;z4=1 600;x1=1 150;y1=1 800;z1=1 200。
这4个传感器的触头在空间中构成一个四面体,其中参考传感器位于箱体的后表面,处于平面的中央,另外三个传感器位于箱体的前表面,且构成的三角形位于平面的中心区域。设时差的测量误差不超过0.02 ms,传感器坐标的测量不超过0.5 mm,声波的传播速度取1 380 m/s,测量误差不超过1 m/s。测量误差均满足均匀分布。仿真时,以最后算法得出的PD源坐标的其实际位置的距离为误差。在1 400 mm的水平面上局部放电定位误差如图2所示。
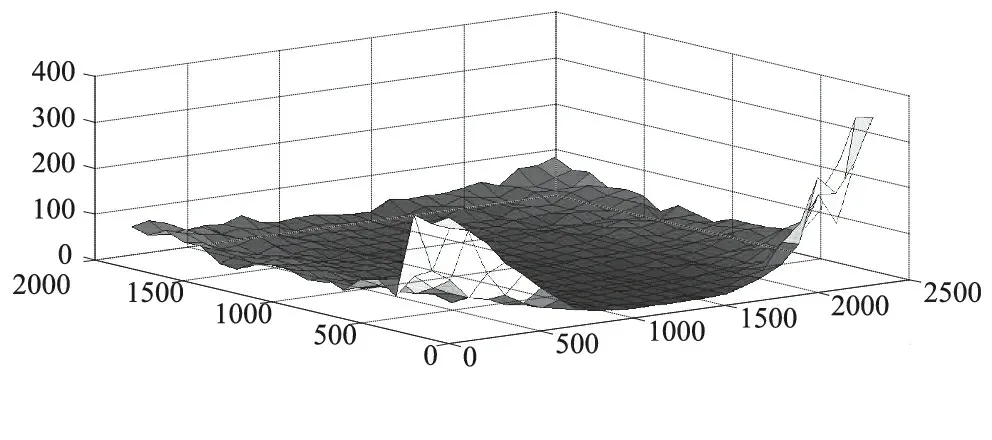
图2 局部放电定位误差分布图谱
可以看出误差较小的区域位于变压器中间区域,误差较高的区域位于变压器棱线处,且距离传感器的位置较近。这时由于当局放源距离传感器较近时,同样的测量误差导致的距离误差所占百分比较高,因此
测量误差较大。
4 结 论
本文给出了变压器局部放电的双曲面定位模型。局部放电定位方程组有4个未知量(x,y,z,T),因此至少需要4个传感器。局部放电定位方程组的解可以直接解算得到,带入最后公式即可得到PD源坐标,计算简便。仿真中对时差、声速、传感器位置加入了误差分析最后定位误差分布,可以得到误差较高的区域总体上离传感器位置较近,且靠近变压器的棱线处。
参考文献:
[1]邱昌容,王乃庆.电工设备局部放电及测试技术[M].北京:机械工业出版社,1994.
[2]Hettiwatte S N,Wang Z D,Crossley P A.Investigation of propagation of partial discharges in power transformers and techniques for locating the discharge[J]. Science,Measurement and Technology,IEE Proceedings.IET,2005,152(1):25-30.
[3]Okabe S,Ueta G,Wada H.Partial discharge signal propagation characteristics inside the winding of oil-immersed power transformer using the equivalent circuit of winding model in the oil[J].Dielectrics and Electrical Insulation,IEEE Transactions on,2012,19(2):472-480.
[4]高鹏路,胡岳,刘斌,等.传感器并联型局部放电监测与定位方法[J].电工技术学报,2014,(2):226-230.
