关于重心基准的坐标转换方法研究

2018-04-09喻国荣冯国鑫张建

全球定位系统 2018年1期

喻国荣,冯国鑫,张建

(东南大学交通学院测绘工程系,江苏南京 210096)

0　引　言

城市与工程测量成果常常采用地方坐标系或独立坐标系,不论是将GNSS等现代测量技术得到的测量数据转换为该坐标系中,还是将该工程测量成果纳入到国家系统中,都需要进行坐标转换。根据需要可选择二维的平面四参数转换模型或三维七参数转换模型,不论哪种模型都无法回避转换模型中平移参数与旋转参数及尺度参数之间的强相关问题[1-3],影响了结果的可靠性。针对于此,产生了坐标重心化方法以及极坐标方法等[3-6],本文对此展开讨论。

1　坐标转换的重心化方法

坐标转换是依据两坐标系下公共点点位坐标得到的转换参数来实现,将B坐标系的坐标转换到A坐标系中的数学模型为

(1)

式中: X(A)P、Y(A)P是公共点P在坐标系A中的坐标; X(B)P、Y(B)P是公共点P在坐标系B中的坐标; X0、Y0称为平移参数; α称为旋转参数； λ称为尺度参数。式(1)对参数α和λ来说是非线性的,通常采用形式参数将式(1)转换为线性方程,即取a=X0,b=Y0,c=λcosα,d=λsinα,则有

(2)

为了计算转换参数,至少需要两个公共点。实际工作中,为了保证可靠性,通常要联测三个以上公共点。当有n(n>2)个公共点时,一般采用最小二乘求解转换参数。设公共点的点位误差相互独立且等精度,则最小二乘法得到的法方程为

Nβ=W,

(3)

式中:

联系人: 喻国荣 Email: 476310930@qq.com

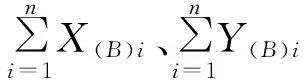
(4)

(5)

(6)于是

(7)

由于平移(坐标重心化)不改变点位的相对关系,即尺度参数与旋转参数是不变的,式(6)中c、d与式(2)相同。可求得尺度参数与旋转参数为

(8)

(9)

平移参数为

(10)

2　坐标转换的讨论

为讨论方便,将由式(3)的解算称为常规四参数方法,由式(6)的解算称为重心化方法。

1) 方法的等价性

旋转角α一般很小,公共点的空间坐标通常在数值上首位不变,对于较小的测区,空间坐标的前几位数字都一样,即几乎相等,坐标重心化相当于将坐标系的原点平移到的点集的重心,一方面使得坐标的数值变得更小,另一方面的优点是法方程矩阵变成了对角阵。这两个优点都使得数值计算变得容易和精确,并不是重心化方法在理论上优于常规四参数法,两种方法都是基于最小二乘原理的,理论基础是统一的、等价的。

2) 参数的相关性

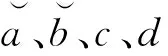
3) 重心不变性

4) 极坐标法

3　算例及分析

为了更好地进行数据分析,设有坐标集如表1所示,坐标系A的坐标是由B坐标系坐标采用参数(abλα)T=(60 m 50 m 9 999.5×10-45")T获得。由于只保留到小数点后三位,即毫米位,相当于坐标系A的坐标存在-0.5 mm到0.5 mm均匀分布的误差。

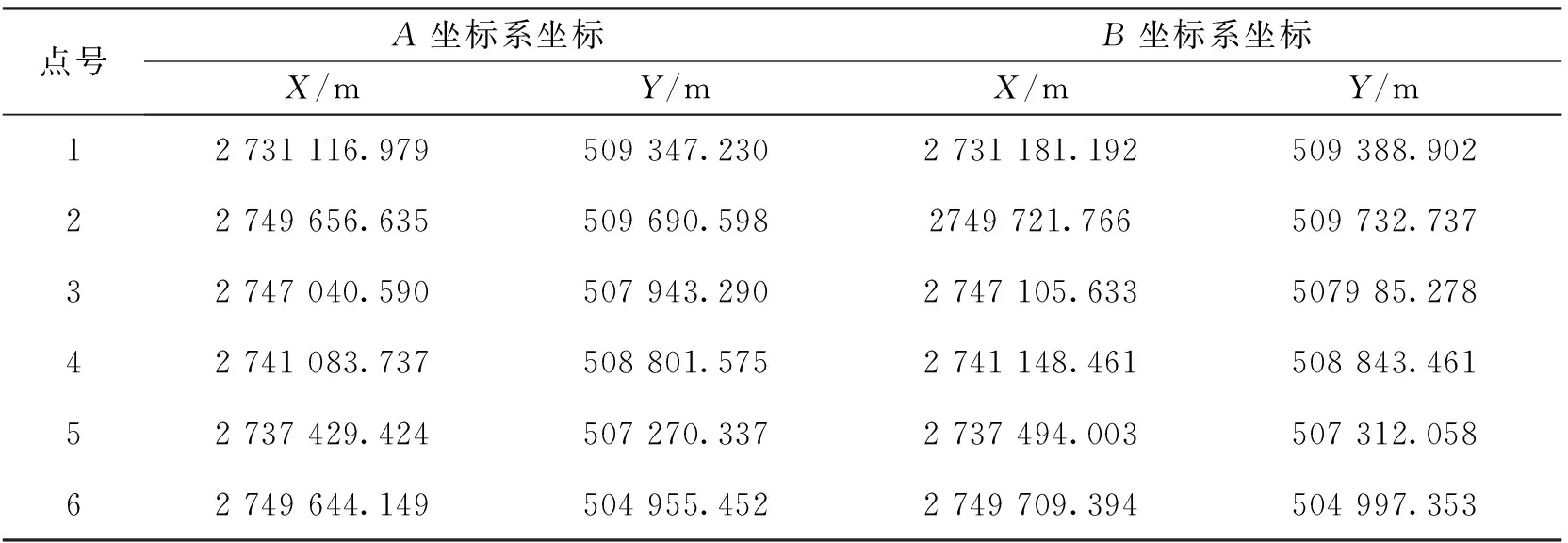
表1　公共点坐标

对坐标系A的坐标施加N(0, 25 mm2)的正态分布误差,以“1、2、3、4”点计算,以“5、6”点作为检查点,计算结果如表2所示。由表2可以看出,四参数方法与重心化方法得到的结果基本相同,其数值差异出现在10-4～10-5量级,可以忽略不计。参数精度及检查点精度与用于计算转换参数的点集的数据精度相当,检查点误差在毫米位相同,差异出现在1/10～1/100 mm位;现代计算技术(计算设备)的进步弥补了四参数方法数值计算的不足;极坐标方法与两种方法存在差异。

为了进一步分析数据精度对转换参数的影响,将坐标系A的坐标施加N(0, 25 cm2)的正态分布误差,相当于坐标系A的坐标受到中误差为σ=5 cm正态分布误差影响,计算结果如表2所示。

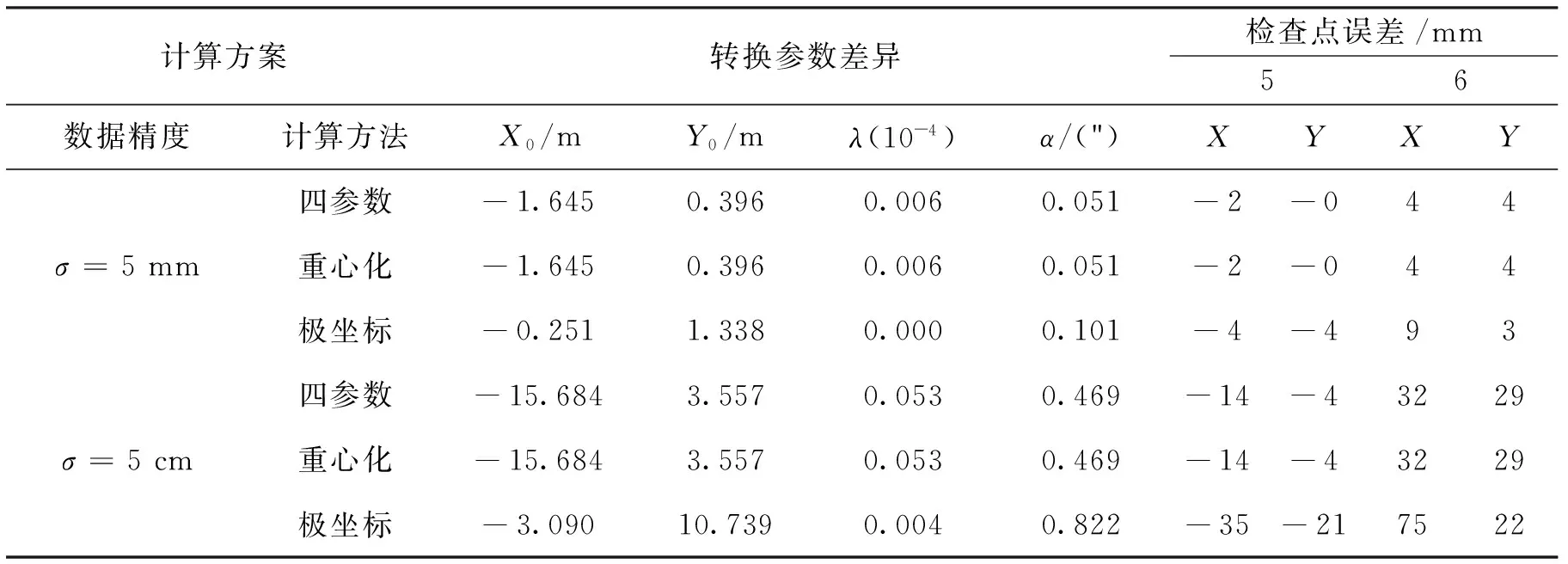
表2　不同坐标转换方法比较

由表2可以看出,当点位精度在厘米级时,四参数方法与重心化方法结果仍基本相同,得到的参数与真值有显著差异,极坐标方法得到的参数受点位误差影响较显著。

当重心化坐标值较小,即点位距“重心”很近时,由于求边长比、求方位角运算对误差非常敏感,即一个微小的误差也引起边长比、方位角的明显变化。比如应用“1、2、3、4、5”点计算参数,以“6”点作为检查点,数据精度σ=5 cm的情形,四参数方法与重心化方法精度在厘米级,而极坐标方法“6”点的误差X=10 cm,Y=14 cm.由于点“4”距“重心”仅263 m,数据精度对边长比、方位角影响剧烈,使得极坐标方法求转换参数几乎没有应用价值。