钢桥面沥青混凝土铺装层静力响应研究

包龙生，谢得璞,2，祁　琳,3

(1. 沈阳建筑大学交通工程学院，辽宁沈阳　110168； 2. 沈阳市市政工程设计研究院，辽宁沈阳　116011； 3. 大连市市政设计研究院有限责任公司，辽宁沈阳　110015)

0　引　言

桥面铺装层是直接承受各种车辆荷载和环境因素作用的功能层，各层在结构上作为一个整体共同发挥着桥面铺装层的路用性能，但是各层受力性能则有所差异，根据各层位功能的不同选择优异的铺装层材料是保证铺装层长期处于良好使用状态的基础[1-3]。双层铺装体系能够对铺装上下层材料分别进行设计，充分发挥材料特性，最大限度地避免同种材料的矛盾双向性。

德国、美国和英国对钢桥面铺装体系展开研究较早，主要采用理论分析、试验分析和数值模拟等手段。Battista等通过有限元计算和试验分析，对正交异性钢桥面铺装体系在交通荷载作用下的疲劳开裂进行了静力学及动力学的分析研究。Tatsuo等运用有限条元、有限棱柱元和有限连接元构建正交异性桥面铺装结构模型，并给定求解方程，该有限元模型中将板肋结构、黏结层和铺装层设定为3个相对独立结构体系进行结构分析。中国自20世纪90年代开始对钢桥面铺装开展了系统研究，在铺装层抗裂疲劳承载能力、受力变形特点及在交通荷载作用下的应力、应变规律等方面都取得了一定的研究成果。

桥面铺装材料的合理选择是保证钢桥面沥青混凝土路面使用性能和使用寿命的关键[4-9]。中国东北寒区常年气温较低，钢桥面的铺装温度比普通的路面温度更低，这对钢桥面铺装材料提出了更高的要求。由于受钢箱梁结构中正交异性板复杂结构的影响，桥面铺装力学反应更为复杂，如何准确分析钢桥面铺装在复杂应力状态下的力学性能是钢桥面铺装设计的关键[10-12]。因此，后丁香大桥采用双层铺装体系，按照层位分工分为表面功能层、整体功能层、防水黏结层3个层位。本文将结合项目所在区域的气候特点、交通条件，考虑钢桥面铺装层的层位功能，选择适宜的铺装材料，同时基于ABAQUS有限元程序，建立后丁香大桥四号桥全桥有限元模型，对钢桥面沥青混凝土铺装层的静力响应进行分析研究。

1　有限元分析方法的基本理论

随着数值模拟方法的不断进步，针对桥面铺装体系的数值模拟诞生了有限元法、有限条法、有限差分法等研究方法，近年来有限元法得到了广泛的应用。有限元分析理论是基于经典的结构力学理论，其目的是研究某结构模型在一定荷载作用下时所受的影响[1-2]。在进行有限元分析前第1步要进行结构的离散化，第2步是假定位移和坐标之间存在的某种函数关系，这种函数关系称为位移模式或者说是插值函数，第3步是根据上一步所选定的位移模式导出关系式，其矩阵方程如下

f=Nδe

(1)

式中：f为单元内任一点的位移列阵；N为形函数矩阵；δe为单元的节点位移列阵。

由节点位移表示的单元应变关系如式(2)所示

ε=Bδe

(2)

式中：ε为单元内任一点的应变列阵；B为单元应变矩阵。

根据本构方程，用节点位移表示的单元应力关系式为

σ=DBδe

(3)

式中：σ为单元内任一点的应力列阵；D为与单元材料有关的弹性矩阵。

利用变分原理建立节点力与单元位移的关系，即单元的平衡方程，如式(4)所示

(4)

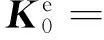
(5)

由式(5)可以看出积分应该在整个单位的体积内。当单位坐标系与结构坐标系不一致时，还需要利用坐标变换矩阵T来完成转换，即

(6)

如果将各单元的刚度矩阵综合起来，就形成整个结构的刚度矩阵，然后将每个单元上的等效节点力矩阵组合起来就构成一个总的荷载列阵。由此可以导出由整体刚度矩阵K、荷载矩阵F和节点位移矩阵δ组成的整体结构平衡方程，即

Kδ=f

(7)

在考虑几何边界条件的前提下，首先由式(7)解出未知位移的值，再用已求出的节点位移和式(4)计算出各单元的应力。

钢桥面结构比普通路面的结构要复杂许多，加之受到钢桥面结构中正交异性钢板横纵加劲肋作用的影响，在加劲肋顶部附近会产生应力集中的现象，因此很难利用弹性薄板理论来求解。利用有限元理论不但能够模拟在不同条件下钢桥和铺装层的受力情况，还可以计算出钢桥模型中任意部位的位移和应力、应变值，进而找出钢桥铺装体系在受力后各项力学指标的变化规律，为铺装层的材料选择和结构设计提供科学有效的依据[13]。

2　钢箱梁桥面铺装整体有限元模型

连续钢箱梁体系的整桥响应对钢桥面铺装体系的力学特性有很大影响，仅仅考虑局部钢桥面铺装复合体系而忽略整桥响应的影响会导致铺装层受力设计值与实际不符。本文以沈阳外环后丁香大桥的四号桥的实际尺寸为基础建立整桥有限元模型，计算分析主体结构最不利特征对桥面体系的影响，得到最不利荷载位置的力学响应。四号桥上部钢箱梁结构形式为48 m+61 m+38 m三跨单箱三室连续梁，主梁高度3.1 m，桥面全宽19.8 m，行车道净宽18.75 m，横断面为单向四车道。钢箱梁主体结构采用Q345qENH钢，顶板支点范围内梁段采用20 mm厚钢板，其余采用16 mm厚钢板。顶板采用U形加劲肋，上口宽300 mm，下口宽170 mm，高度300 mm，U形加劲肋厚度取8 mm，标准间距600 mm，顶板端部采用板肋加劲，板厚18 mm，高度210 mm，标准间距300 mm。底板中支点附近采用20 mm厚钢板，其余采用16 mm厚钢板。腹板采用16 mm厚钢板，沿腹板高度方向设置2道180 mm×16 mm平板加劲肋。横隔板标准间距3 m，厚度20 mm。钢板厚度及参数见表1。

四号桥的钢桥面铺装层采用树脂沥青组合体系(ERS)，铺装厚度为70 mm。按照《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)对RA05及SMA13两种材料在20 ℃±2 ℃时进行小梁弯曲试验，得到2种材料的弹性模量见表2。

根据后丁香大桥四号桥结构尺寸，利用ABAQUS6.10有限元软件建立桥梁整体有限元模型。ABAQUS有限元软件可以选择杆单元、实体单元、壳单元、连续壳单元等多种单元类型进行不同构件的建模。本文主要研究桥面铺装层的受力情况，局部需要进行网格细化，采用8节点实体缩减积分单元C3D8R进行桥面铺装层的模拟。大跨径桥梁中，顶板、底板及U肋在厚度方向尺寸远小于另外两维尺寸，钢箱梁采用4节点缩减积分壳单元S4R进行模拟。

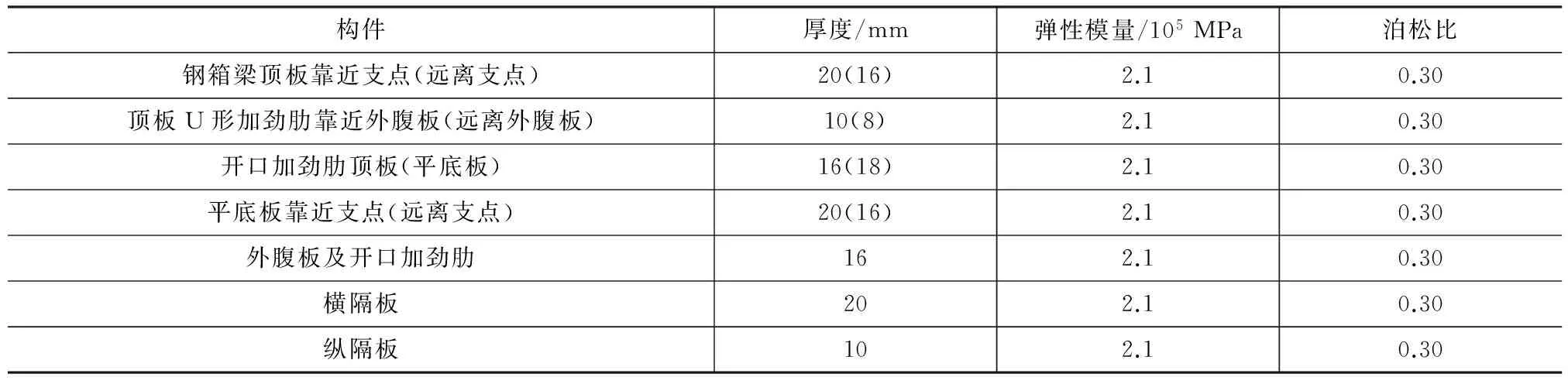
表1　后丁香大桥四号桥钢箱梁材料参数Tab.1　Material Parameters of Steel Box Girder of No.4 Houdingxiang Bridge

表2　后丁香大桥四号桥ERS铺装结构层形式及材料参数Tab.2　Structural Form and Material Parameters of ERS Deck of No.4 Houdingxiang Bridge

图1　钢箱梁有限元模型局部划分效果图Fig.1　Local Partition Effect Diagram of Finite Element Model of Steel Box Girder

图2　钢箱梁有限元模型整体划分效果图Fig.2　Overall Partition Effect Diagram of Finite Element Model of Steel Box Girder

划分单元时，为了既保证运算的精度又能提高运算的速率，对车轮荷载作用区域的划分较细，单元的尺寸设定为50 mm×50 mm。对于那些距离车轮荷载较远的区域，单元的尺寸设定为500 mm×500 mm，最终的划分结果如图1，2所示。全桥共划分Solid单元205 020个、Shell单元200 153个。边界条件为在桥墩处限制垂直方向的位移，1号桥墩是固支约束，桥的两端约束了转动。在建立钢箱梁梁段有限元模型以及全桥有限元模型时，有如下的基本假定：

(1)铺装层材料的线弹性假定：假定沥青铺装材料是完全弹性、均匀、连续且各向同性的材料。

(2)界面连续假定：所有层间完全连续。

(3)桥面铺装层之间以及铺装层与主梁钢顶板之间黏结可靠，两者间不脱空。

(4)各层材料不考虑自重的影响。

(5)桥面铺装层相对较薄，不考虑铺装层内的温度差。

(6)计算过程中钢材、沥青混凝土的泊松比均不随温度变化。

3　钢桥桥面铺装层静力响应分析

3.1　全桥最不利荷载位置的计算分析

当荷载作用于桥梁的某一位置时，铺装层承受的荷载作用最大，对铺装层的损伤最严重，这一位置称为全桥最不利荷载位置[14]。本文首先对全桥模型施加车道荷载，通过对比不同作用状态下桥面铺装层的力学响应，找到铺装层在车道荷载作用下的全桥最不利荷位。

车道荷载的大小由荷载的长度以及集度组成，荷载集度取值50 kPa。后丁香大桥为单向四车道，每个车道的宽度为3.75 m，按照车道荷载作用的范围，横桥向位置分别选择单车道、双车道、四车道，纵桥向位置分别选择L，L/2，L/4，共9种工况，计算每层铺装的层间最大拉应力、最大剪应力，结果见表3。汽车荷载根据车道数横桥向折减，双车道横桥向折减系数为1，四车道横桥向折减系数为0.67，纵桥向不考虑折减。桥梁冲击系数μ的取值参照桥梁结构设计说明，正弯矩区采用0.04，负弯矩区采用0.045。

表3　各种工况下全桥最不利荷载位置的拉应力、剪应力计算值Tab.3　Calculation Values of Tensile Stress and Shear Stress at Most Unfavorable Load Position Under Various Conditions

由表3可知，SMA13层、RA05层无论是横桥向的最大拉应力或剪应力，还是纵桥向的最大拉应力或剪应力及位移值，均出现在工况2，即纵桥向全桥加载，横桥向双车道加载。纵桥向加载从大到小依次为L，L/2，L/4，横桥向加载从大到小依次为B/2，B，B/4，其计算结果与荷载大小呈正比关系，所以车辆质量的大小也是引起桥面铺装破坏的主要原因。图3为横桥向双车道加载，纵桥向全桥加载的应力云图。

图3　双车道全桥加载应力云图Fig.3　Loading Stress Nephogram of Two Lane Full Bridge

由图3可知，纵桥向最不利荷载位置出现在1号桥墩处，横桥向出现在外侧腹板位置，该位置即为全桥最不利荷载位置。这是因为车辆荷载作用下，加劲肋、横隔板、纵腹板顶部以及连续梁的桥墩支撑处铺装层表面出现负弯矩，钢桥面铺装层易出现裂缝。计算结果也揭示了引言中调查的2座桥梁首先在纵桥向边缘腹板处和桥墩支撑处出现横向裂缝的原因。

3.2　车辆荷载轮胎接地压力分析

汽车荷载通过车轮胎作用于桥面，目前路面设计采用双轮组单轴载100 kN为标准轴载，即BZZ-100，双轮组每个轮胎上分担的荷载为25 kN，轮胎稳定内压为0.7 MPa，接地面积为等直径的双圆形。轮胎的实际结构组成非常复杂，即使是光面轮胎对其进行完全建模将也非常繁琐，本文利用有限元方法建立轮胎三维有限元模型，分析轮胎接地压力分布情况，选用265/70R19.5载重汽车子午线光面轮胎，其主要结构参数及规格根据文献选用，见表4。由于桥面铺装在荷载作用下也会发生变形，且会随着铺装结构组合形式和材料组成的不同而产生变化，假设轮胎作用区域为刚性体。

轮胎是由橡胶、帘布层和带束层构成的多层结构，力学性能表现为黏弹性、非线性和各向异性，对轮胎基体的橡胶材料定义了Mooney超弹性本构模型，采用8节点缩减积分单元C3D8R进行建模，网格尺寸为20 mm×20 mm，轮胎层模型的材料参数根据文献选取，见表5。

笔者利用有限元方法建立不同种类与不同花纹类型轮胎的三维有限元模型，分析了轮胎接地压力的分布情况，认为把荷载作用面积简化成矩形是合理的。轮胎在静态负载过程中的Von-Mises等效应力云图如图4所示，接地压力分布如图5所示。从图5中可以发现，在靠近轮胎边缘两侧存在接触压力集中现象，接地压力峰值达到1.066 MPa，平均值在0.72 MPa左右，轮胎与桥面铺装层接触面横向宽度为220 mm，纵向宽度为180 mm，接地压力形状近似为矩形。接触面积模拟结果与BZZ-100荷载简化的单圆面积较为接近，接地压力平均值与标准荷载幅值0.7 MPa较为接近。静力计算中把标准轴载的荷载图式简化成尺寸为220 mm×180 mm的矩形，荷载分布采用0.72 MPa均布荷载。

将双轮组荷载进行有限元模型分析，建立双轮组轮胎接地模型，竖向荷载为50 kN，静态负载过程中的Von-Mises等效应力云图如图6所示，接地压力分布如图7所示。

双轮组轮胎与单轮轮胎的接地压力相同，轮胎与桥面铺装层接触面横向实际宽度为440 mm，接地作用范围宽度为500 mm，纵向宽度为180 mm，接地压力形状近似为矩形，若将双轮组荷载等效成为矩形荷载，则矩形荷载尺寸为500 mm×180 mm，荷载集度为0.72 MPa。

3.3　局部最不利荷载位置的计算分析

确定了铺装层全桥最不利荷载位置后，便能够在此基础上进行局部最不利荷载位置的计算。纵桥向选择全桥最不利荷载位置计算，得到的最大跨中截面应力为最大的桥墩支点截面，横桥向选择第2行车道施加车辆荷载，荷载轴重取标准轴载BZZ-100，按照前文把标准轴载的荷载图式简化成尺寸为220 mm×180 mm的矩形，荷载分布采用0.72 MPa均布荷载，如图8所示，以行车道中心C点为对称中心，横向间隔0.3 m，计算横向不同位置拉应力、剪应力变化情况，结果如图9所示。

表4　265/70R19.5载重汽车子午线轮胎结构参数Tab.4　Structural Parameters of Radial Tire for 265/70R19.5 Truck

表5　265/70R19.5载重汽车子午线轮胎材料参数Tab.5　Material Parameters of Radial Tire for 265/70R19.5 Truck

图4　单轮轮胎Von-Mises等效应力云图(单位:MPa)Fig.4　Von-Mises Equivalent Stress Nephogram of Single Wheel Tie (Unit:MPa)

图5　单轮轮胎桥面接地压力(单位:MPa)Fig.5　Single Wheel Tire Bridge Ground Pressure (Unit:MPa)

图6　双轮组轮胎Von-Mises等效应力云图(单位:MPa)Fig.6　Von-Mises Equivalent Stress Nephogram of Double Wheel Tires (Unit:MPa)

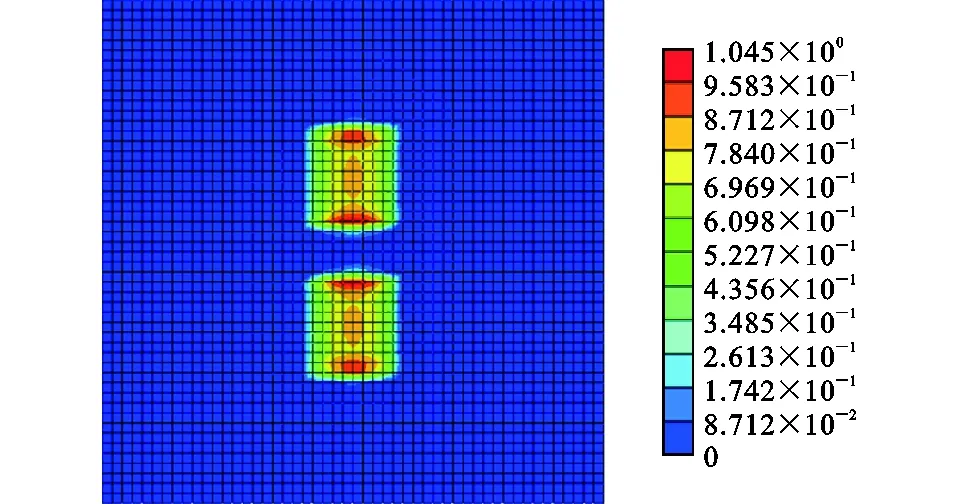
图7　双轮组轮胎桥面接地压力(单位:MPa)Fig.7　Double Wheel Tires Bridge Ground Pressure (Unit:MPa)

图8　车辆荷载横向加载位置(单位:mm)Fig.8　Lateral Load Position of Vehicle Load (Unit:mm)

图9　桥墩及跨中横桥向不同位置应力变化曲线Fig.9　Stress Change Curves of Piers and Midspan Bridges at Different Positions

由图9可知，除横向剪应力外，无论是桥墩还是跨中，拉应力及剪应力的最大值均出现在对称行车道中心0.9 m的B，D位置，该位置为车轮荷载作用位置，即横桥向车轮荷载作用的位置即为最不利的位置。对于纵向拉应力及横向拉应力，桥墩位置大于跨中位置，RA05层大于SMA13层。横向拉应力大于纵向拉应力，说明桥面铺装层表面更易出现纵向裂缝。对于纵向剪应力，桥墩位置和跨中位置几乎相等，RA05层大于SMA13层，说明桥面铺装层与桥面板之间更易发生滑移及脱层。横向剪应力的幅值没有出现在车轮荷载作用位置，而是出现在荷载作用的相邻两侧，大小相等，方向相反。

正交异性桥面板纵向U形加劲肋的构造对顶板有局部加强作用，当双轮组荷载作用于U形加劲肋的不同位置时，铺装层的拉应力及剪应力会有所区别。为此，选择桥墩及跨中2个截面，按照双轮组荷载与U形加劲肋的位置关系，选择3种工况，如图10所示，计算最大拉应力、最大剪应力及最大位移，计算结果如图11所示。

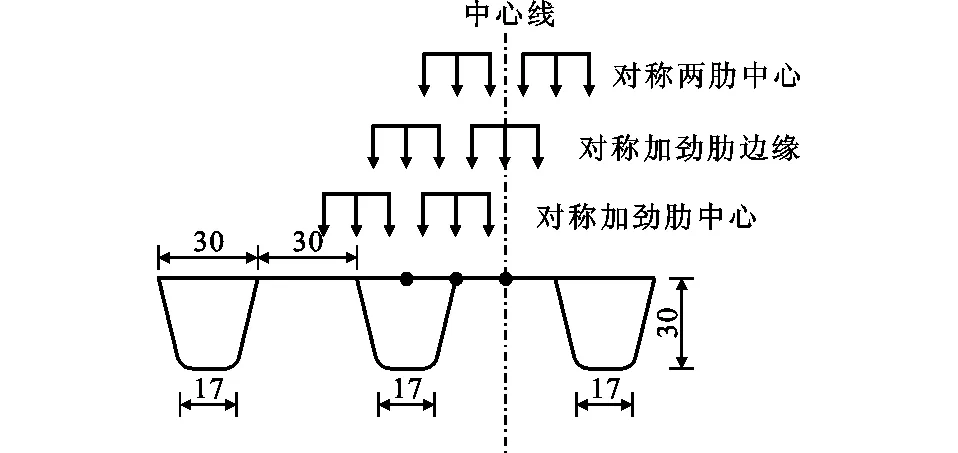
图10　横向加载工况(单位:mm)Fig.10　Lateral Loading Cases (Unit:mm)

由图11可知，RA05层和SMA13层拉应力及剪应力的最大值均出现在双轮组荷载对称作用纵向U肋边缘位置，除RA05层最大横向剪应力出现在跨中，其余均出现在桥墩位置。桥墩及跨中横向拉应力数值均大于纵向拉应力，桥墩处的拉应力大于跨中的拉应力，RA05层的拉应力及剪应力均大于SMA13层。

综上所述，得到静态局部最不利荷载位置，即桥墩处双轮组荷载对称U肋边缘位置，应力峰值出现在车轮下。标准轴载BBZ-100作用下的应力、位移最大值见表6。

4　结语

(1)全桥最不利荷载位置纵桥向出现在1号桥墩处，横桥向出现在外侧腹板位置，该位置即为全桥最不利荷载位置。

(2)车轮荷载作用下，RA05层和SMA13层拉应力及剪应力的最大值均出现在双轮组荷载对称作用纵向U肋边缘位置，除RA05层最大横向剪应力出现在跨中，其余均出现在桥墩位置。桥墩及跨中横向拉应力数值均大于纵向拉应力，桥墩处的拉应力大于跨中的拉应力，RA05层的拉应力及剪应力均大于SMA13层。

(3)通过计算，得到了后丁香大桥四号桥的SMA13层和RA05层在标准轴载BBZ-100作用下的应力、位移峰值。

图11　横向加载不同位置应力对比Fig.11　Stress Contrasts at Different Positions During Lateral Loading

表6　局部最不利荷载位置下铺装层应力、应变最大值Tab.6　Maximum Stress and Strain of Lower Pavement Layer at Local Unfavorable Load Position

参考文献：

[1]曹鹏.沥青路面多尺度力学分析方法及模型研究[D].哈尔滨:哈尔滨工业大学,2014.

CAO Peng.Research on Multiscale Mechanical Analysis Method and Model of Asphalt Pavement[D].Harbin:Harbin Institute Technology,2014.

[2]黄卫.大跨径桥梁钢桥面铺装设计[J].土木工程学报,2007,40(9):65-77.

HUANG Wei.Design of Deck Pavement for Long-span Steel Bridges[J].China Civil Engineering Journal,2007,40(9):65-77.

[3]AHN J H,LEE C G,WON J H,et al.Shear Resistance of the Perfobond-rib Shear Connector Depending on Concrete Strength and Rib Arrangement[J].Journal of Constructional Steel Research,2010,66(10):1295-1307.

[4]黄继成,叶奋.钢桥面沥青铺装出现的问题及其防治[M].上海:同济大学出版社,2007.

HUANG Ji-cheng,YE Fen.Problems and Prevention of Asphalt Pavement on Steel Deck[M].Shanghai:Tongji University Press,2007.

[5]赵锋军,李宇峙.西陵长江大桥沥青铺装大修工程关键技术[J].公路交通科技,2012,29(5):52-61,82.

ZHAO Feng-jun,LI Yu-zhi.Key Technology of Asphalt Pavement Overhaul for Xiling Yangtze River Bridge[J].Journal of Highway Transportation Research and Development,2012,29(5):52-61,82.

[6]余锦州.马房大桥钢桥面沥青混凝土铺装层设计[J].公路,2004(8):47-50.

YU Jin-zhou.Design of Asphalt Concrete Pavement of Mafang Bridge Steel Deck[J].Highway,2004(8):47-50.

[7]Al-DARZI S Y K,CHEN A R,LIU Y Q.Finite Element Simulation and Parametric Studies of Perfobond Rib Connector[J].American Journal of Applied Sciences,2007,4(3): 122-127.

[8]熊巍,雷宗建,刘松.军山大桥钢桥面铺装大修养护设计及应用[J].中国公路,2013(21):126-127.

XIONG Wei,LEI Zong-jian,LIU Song.Overhaul Maintenance Design and Application of Steel Bridge Deck Pavement of Junshan Bridge[J].China Highway,2013(21):126-127.

[9]VIANNA J D C,COSTA-NEVES L F,VELLASCO P C G D S,et al.Structural Behaviour of T-Perfobond Shear Connectors in Composite Girders:An Experimental Approach[J].Engineering Structures,2008,30(9):2381-2391.

[10]胡晓燕.大跨度公路桥梁车桥耦合振动响应研究[D].武汉:武汉理工大学,2009.

HU Xiao-yan.Research on Vehicle-bridge Coupling Vibration of Long-span Highway Bridge[D].Wuhan:Wuhan University of Technology,2009.

[11]肖维.五河口大桥沥青混凝土铺装层力学分析及结构组合研究[D].南京:东南大学,2006.

XIAO Wei.Mechanics and Structural Combination Study of Asphalt Pavement on Wuhekou Long-span Concrete Bridge[D].Nanjing:Southeast University,2006.

[12]EN 1994-2:2005,Eurocode 4:Design of Composite Steel and Concrete Structures.Part2:General Rules and Rules for Buildings[S].

[13]罗桑,钱振东,陆庆.基于动态频率扫描试验的环氧沥青混合料动态模量研究[J].石油沥青,2010,24(4):55-58.

LUO Sang,QIAN Zhen-dong,LU Qing.Research on Dynamic Modulus of Epoxy Asphalt Mixed by Dynamic Frequency Sweep Test[J].Petroleum Asphalt,2010,24(4):55-58.

[14]KIM H Y,JEONG Y J.Experimental Investigation on Behaviour of Steel-concrete Composite Bridge Decks with Perfobond Ribs[J].Journal of Constructional Steel Research,2006,62(5):463-471.