Probabilistic Quantitative Temporal Constraints:Representing, Reasoning, and Query Answering
2018-04-08PaoloTerenzianiandAntonellaAndolina
Paolo Terenziani and Antonella Andolina
1.Introduction
The representing and reasoning about time are the major issues to be considered in all reasoning tasks which take account of a dynamic domain. In particular, they are important tasks in many areas of artificial intelligence (AI), such as planning,scheduling, human-machine interaction, natural language understanding, diagnosis, and robotics. Particularly, in all such areas, the need of representing and reasoning with temporal constraints between actions (e.g., action B must be started at least 1 hour after the end of action A) is of primary importance.
The approaches explicitly focusing on temporal constraints(which are the focus of this paper) can be distinguished on the basis of whether they focus on the qualitative (e.g., A before B)or quantitative (e.g., the delay between the end of B and the start of A is 10 minutes) aspect of temporal knowledge (see the surveys in [1]-[3]). Among the approaches of the first kind, the interval algebra[4]and the point algebra[5]deal with a qualitative representation of temporal knowledge relative to intervals and points, respectively. On the other hand, quantitative approaches,such as those in [6] and [7], deal with metric temporal statements concerning points. Furthermore, hybrid approaches have been proposed in order to combine the expressiveness capabilities of these formalisms[8],[9], where qualitative and metric information are integrated in a single model. All of these proposals rely on the framework of the constraint satisfaction problem(CSP), in which they approach the relevant reasoning tasks by representing the temporal objects as variables with temporal domains, and the available temporal knowledge as a set of constraints between these variables. Unfortunately,these temporal constraint-based reasoning approaches inherit from the CSP a number of fundamental limitations, mainly related to a lack of flexibility and a limited representation of uncertainty: In all such approaches, temporal constraints are represented by a set of “equally possible” precise temporal relations/constraints between two time units.
“In classical CSPs, knowledge is embedded in a set of hard constraints, each one restricting the possible values of a set of variables. However constraints in real world problems are seldom hard, and CSPs are often idealizations that do not account for the preference among feasible solutions.”[10]
While usually, in real world problems, constraints are satisfied to a degree, rather than satisfied or not satisfied, only“hard” and “crisp” temporal constraints can be represented in classical approaches, making it impossible to tolerate partial violation of constraints and to account for preferences among feasible solutions. As a practical example, consider the development of lumbalgia pathologies[11]. Brucellosis is one infectious pathology which may be the origin of serious lumbalgia problems. It is usually composed of an inoculation event, an initial period, and a period of ondulating fever and,finally, it reaches the state of an intervertebral affection.There is some (vague) knowledge about the temporal evolution of Brucellosis cases: Just as an example, the initial period usually starts at the time between one and three weeks after the inoculation event, although extreme cases it ranges from starting at the very inoculation time up to four weeks after. Thus, a “classical” solution, which cannot accommodate different preferences/priorities/possibilities/probabilities for the different alternatives, is not expressive enough to cope with the problem. Moreover, a related issue concerns the inability to associate either different priorities to constraints,with the aim of satisfying as much as possible the most important ones, or probabilities, to represent the probability that a given constraint holds (in the common case of alternative possible constraints). Finally, classical approaches account for uncertainty, which pervades most practical problems, in a limited way. For instance, in interval algebra a constraint is expressed as a set of equally possible atomic relations which can hold between two intervals, so that the uncertainty relative to their mutual position is only related to the cardinality of this set. It is impossible to express more refined knowledge concerning the uncertainty affecting constraints, as in the case where the presence of a particular constraint is not certain, but we have some idea about its degree of “plausibility”, or its probability.
In order to overcome the above limitations, the CSP formalism has been extended in a fuzzy direction, by replacing classical “hard” and “crisp” constraints with“soft” and “non-crisp” constraints.
1.1 Non-Crisp CSP: General Approaches
Bugarín et al.[12]discussed a wide number of approaches which explicitly include time as another decision variable in fuzzy propositions and rules. Restricting the attention to CSP approaches only, a number of temporal reasoning approaches based on the fuzzy[10]CSP have been devised. For instance,Barro et al.[13]introduced a model for the representing and handling of fuzzy temporal references. They defined the concepts of date, time extent, and interval, according to the formalism of possibility theory, and relations between them,interpreted as constraints on the distances and projected onto fuzzy temporal constraint satisfaction networks. Vila and Godo[14]proposed a propositional temporal language based on fuzzy temporal constraints to cope with domains where the knowledge of propositional nature and explicit handling time,imprecision, and uncertainty were required. The language was provided with natural possibilistic semantics to account for the uncertainty issued by the fuzziness of temporal constraints.They also presented an inference system based on specific rules dealing with the temporal constraints and a general fuzzy modus ponens rule where the behaviour was shown to be sound. Kamide and Koizumi[15]have recently proposed an inconsistency-tolerant probabilistic tree logic. Recently,Gammoudy et al. have proposed a model of Allen’s qualitative relations between fuzzy time intervals[16], while Billet et al. have considered “ill-known” time intervals[17].
In the area of scheduling/planning, several approaches have faced the fact that, in planning/scheduling contexts, temporal constraints should not be all considered in the same way, since some of them are controllable and the others are not. In this context, the simple temporal network with uncertainty (STNU)has been introduced to extend the simple temporal network(STN)[18], by setting bounded uncertainty to cope with uncontrollable events. The STNU has also been extended with a probabilistic representation of the uncertainty[19]. In the probabilistic extension, information regarding the distribution of uncontrollable events allows planning for outcomes which are more likely. More recently, a large amount of work has been devoted to temporal planning with uncertainty, leading to different solutions, including temporal plan networks with uncertainty[20], disjunctive temporal problems with uncertainty[21], conditional STNU[22], simple temporal problem(STP) under uncertainty[23], and probabilistic temporal plan networks[24]. Fang et al.[25]introduced the probabilistic simple temporal network (pSTN), a probabilistic formalism for representing temporal problems with bounded risk and utility over event timing. They also introduced a constrained optimisation algorithm for pSTNs that achieved compactness and efficiency, for strong controllability[18], to provide robust scheduling. Yorke-Smith et al.[26]have proposed a unifying framework, in which both preferences and uncertainty (related to the controllability problem) were coped with in an integrated approach. Recent planning approaches have focused on the treatment of temporal constraints with preferences[27],[28].
1.2 Non-Crisp Temporal Constraints
While the above approaches cope with different ranges of phenomena, an important mainstream of AI research (in which our approach is located) has focused specifically on the representation of “non-crisp” temporal constraints between points/intervals, and on the propagation of such constraints[29]. Concerning qualitative constraints, Ryabov et al.[30]attached a probability to each of Allen’s basic interval relations. An uncertain relation between two temporal intervals was represented as a disjunction of Allen’s probabilistic basic relations. Using the operations of inversion, composition, and addition, defined for this probabilistic representation, they presented a path consistency algorithm. A similar probabilistic approach has been proposed more recently by Mouhob and Liu[31], as an adaptation of the general probabilistic CSP framework. On the same line of research, Badaloni and Giacomin[32]extended Allen’s interval-based framework to associate a preference degree to relations between intervals. On the other hand, to the best of our knowledge, “non-crisp” quantitative temporal constraints have only been considered by the approach by Khatib et al.[33]. They extended constraint-based temporal reasoning (and, in particular, the STP and temporal constraint satisfaction problem (TCSP) frameworks[6]) to allow for reasoning about temporal preferences, and the complexity of the resulting formalism was examined. While in general such problems are NP-complete, they showed that, if one exploits C-semirings in the treatment of preferences, tractability can be achieved. The approach proposed by Khatib et al. is the closest one to ours proposed in the literature, since we are both based on STP. However, a main difference shows up: While Khatib et al. dealt with preferences, we cope with probabilities.Thus, for instance, completely different operations (of intersection and composition) are provided for temporal reasoning.
1.3 Goals of the Proposed Approach
We propose an approach that overcomes the current treatment of non-crisp temporal constraints in two main aspects: We propose the approach that 1) supports the association of probabilities to quantitative temporal constraints and 2) copes with query answering about such constraints for the first time.
Considering the aspect 1), there is no doubt about the extensive use and ascertained usefulness of probabilities (e.g.[34]) and of quantitative temporal constraints (e.g., [1]-[3]) in the AI context (e.g., to deal with knowledge representing or planning[34]). Therefore, the absence of a framework in which a probability distribution can be associated with quantitative temporal constraints is a severe limitation of the current literature, which we aim at overcoming with our work.
Considering 2), it is worth noticing that, in most practical applications, supporting temporal reasoning to check the consistency of a knowledge base of temporal constraints (i.e., in order to check whether they admit a solution) is not enough. Indeed, it is important to be able to query the temporal constraints, e.g., to check whether a given instantiation of some of the constraints (possibly a partial instantiation) is possible (i.e., it is part of at least a solution). For instance, in the approaches based on the hypothesizing and test paradigm—like, in planning and scheduling, queries to the temporal constraints may be fundamental to investigate the temporal feasibility of some partial solution. Surprisingly, despite the importance of such a task, query answering has been mostly neglected in the context of temporal constraints[35], and has been completely neglected in the context of non-crisp temporal constraints. In our paper, we overcome such a significant limitation of the current literature, proposing an approach for querying probabilistic quantitative temporal constraints (PQTCs).
1.4 Organization of the Paper
In Section 2, we briefly remind the basics about “crisp”(i.e., without considering probabilities) quantitative temporal constraints, temporal reasoning, and query answering operating on them. In Section 3, we introduce our representation of PQTCs. In Section 4 we describe our temporal reasoning approach. Section 5 proposes our query language and our query answering approach. Finally, Section 6 contains the conclusions.
2.Preliminaries about Crisp Quantitative Temporal Constraints
Quantitative temporal constraints involve metric time and are very frequent in many applications and domains.They include dates (e.g., “John arrived on October 10, 1999 at 10:00”), duration (e.g., “John worked for 3 hours”), and delays (e.g., “John arrived 10 minutes after Mary”).Different types of approaches have been developed within the AI community in order to deal with quantitative temporal constraints (see the surveys in [1]-[3]). In this section we introduce some preliminaries regarding one of the most used approaches, i.e., STP[6]. Readers familiar with these topics can safely skip this section.
2.1 Representing STPs
An STP constraint is a bound on the differences of the form, where x and y are time points and c and d are the numbers whose domains can be either discrete or dense. The intuitive temporal interpretation of the constraint is that the temporal distance between the time points x and y is between c(minimum distance) and d (maximum distance). It is possible to specify strict inequalities (i.e., <), and –∞ and +∞ can be used to denote infinite lower and upper bounds, respectively(i.e., no lower or upper bound). An STP is a set of constraints, i.e. a conjunction of STP constraints.
Two representations are often used for STPs: Graph and matrix. An STP is represented as a graph whose nodes correspond to the time points of the STP and the arcs are labeled with a weight, representing the maximum temporal distance between the temporal points. A constraintis thus represented by two edges corresponding to the pair of inequalitiesand. For short,usually the arcs are labeled by the interval [c, d]. Alternatively,an STP is represented as a matrix D of size N×N where N is the number of temporal points and where the elementrepresents the maximum distance d between the points x and y.The minimum distance c is represented as the maximum distancebetween y and x.
Example. Let us consider the following information concerning three time points A, B, and C: B occurs between 2 and 4 hours after A, C occurs between 2 and 4 hours after B and between 2 and 6 hours after A. This information can be represented by the following STP S composed by a conjunction of three STP constraints (in this example we assume that the domain is the integers). We provide also the representations of S as a graph and as a matrix, as shown in Fig. 1.

2.2 Consistency and Minimal Network
Temporal reasoning on an STP is performed by propagating the constraints and obtaining the minimal network[6]. The minimal network is the tightest equivalent STP, i.e., an STP where the minimum and maximum implied distances between each pair of points are made explicit. Computing a minimal network of an STP corresponds to computing the all-pairs’ shortest paths of the graph; an algorithm such as the Floyd-Warshall’s one can be used[6]. Such an algorithm can also determine the consistency of an STP by checking whether it contains negative cycles. Floyd-Warshall’s algorithm is shown in Table 1; in the algorithm,denote the time points(e.g., starting/ending points of actions) anddenotes the constraint between the points i and j, i.e., the interval,such that.

Fig. 1. Representations of S as: (a) graph and (b) matrix.

Table 1: Floyd-Warshall’s algorithm
Property. Floyd-Warshall’s algorithm is correct and complete on the STP, i.e., it performs all and only the correct inferences while propagating the STP constraints[6].Its temporal computational cost is cubic in the number of time points.
Applying Floyd-Warshall’s algorithm to the STP S in the example allows to determinate the minimal network of S,where, for example, it is made explicit that, if B occurs at least 2 hours after A and C at least 2 hours after B, C must occur at least 4 hours after A. The details are shown in Fig. 2.
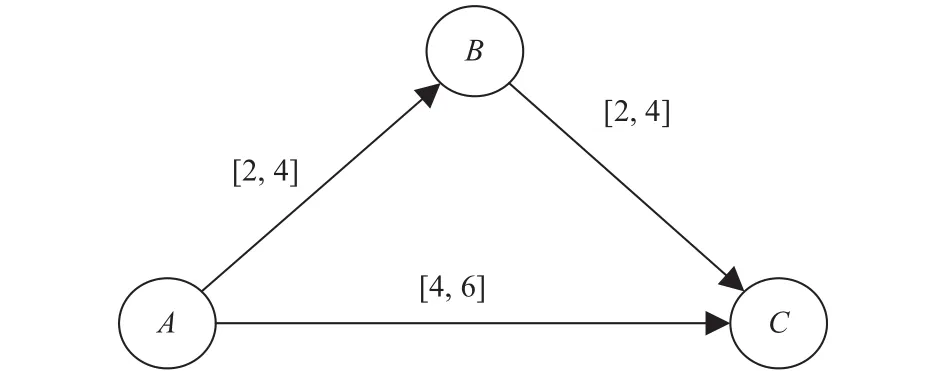
Fig. 2. Graph representation of S after the application of Floyd-Warshall’s algorithm.
2.3 Solutions of an STP
Thanks to the properties of the minimal network, one is granted that each value of a constraint of the minimal network belongs to a solution of the STP[6]. For example, given the constraintin the minimal network of the STP S,the value 3 for the distance between A and B (i.e., if B is exactly 3 hours after A) is part of at least a solution.Specifically, this value corresponds to the two solutions of the STP where 1) C–B=2 and C–A=5 and 2) C–B=3 and C–A=6.However not every combination of values admitted by the constraints in the minimal network results in a solution of the STP. Consider, for example, B–A=3 and C–B=4; while they are individually admitted by the constraints in the minimal network of S, they cannot be extended to a solution: In fact, no consistent value can be chosen for C–A (in fact B–A=3 and C–B=4 are the values that belong to two different solutions).
If an STP changes because a new tighter constraint is added, a new constraint propagation is required because it is necessary to take into account the consequences of the change on the other constraints, which can possibly be tightened, and to reestablish the minimal network. For example, in S, if we tighten the constraint B–A to(i.e., we rule out the value B–A=2), also the other two constraints would be tightened and the new minimal network has(in fact, the value C–A=4 is no longer possible) and(in fact, the value C–B=4 is also no longer possible).
2.4 Querying an STP
Given an STP, it is useful to ask queries and, in particular,whether some constraints are possible with regard to the STP(i.e., they are consistent with the STP or, equivalently, there is a solution of the STP where the constraints are satisfied[35]). The discussion below assumes that the minimal network has already been obtained.
Asking a query with one constraint is equivalent to determine whether the constraint is consistent with the minimal network of the STP, i.e., whether at least one value admitted by the query constraint belongs to a solution of the STP. In the example, asking whether a constraint such asis possible with regard to the STP S, implies to determine whether at least one value between 3 and 6 for B–A belongs to a solution of the STP S. Thus, it is possible to answer such a query by verifying whether the intersection between the query constraint and the corresponding constraint in the minimal network is empty. In the example, thus the constraint is possible.
When a query is composed by more than one constraint, it is not possible to answer it by simply inspecting the minimal network. In fact, for reasons derived from the discussion above,constraints can be individually consistent but inconsistent when considered together. For example, in S the constraints are individually possible but,taking them together, they do not correspond to any solution of S. Thus, in order to answer to queries with two or more constraints, such constraints must be added to the STP and then be propagated by using the Floyd-Warshall’s algorithm to detect whether they are conjunctively consistent (i.e., no negative cycle has been created).
3.Probabilistic Quantitative Temporal Networks
In this work, we aim at extending quantitative (i.e., metric)temporal constraints to support the possibility to associate probabilities with alternative constraints. As most approaches focus on quantitative constraints (see [1]-[3]), we base our approach on the notion of the distance between time points.Indeed, we base our approach on STP[6]. In our approach, the distances between two points are a convex and discrete set of alternatives, from a minimum distance to a maximum distance,and we associate a probability to each distance.
Definition. Probabilistic quantitative temporal label(PQTL), probabilistic quantitative temporal constraint (PQTC),and probabilistic temporal network (PTN).
A PQTC is a constraint of the form, whereandare time points.
Note. For the sake of readability, in each probabilistic temporal constraint, we order the distances(i.e.,but our approach is mostly independent of such a convention.
Example 1. For the sake of simplicity, let us work at the granularity of hours, and let us denote the beginning of a given day by t0. Suppose we want to model the fact that John wakes up (time point t1) at 6 with the probability of 0.2, at 7 with 0.6,or at 8 with 0.2, has lunch (time point t2) at 12 with 0.3, 13 with 0.5, or 14 with 0.2, has dinner (time point t3) at 18 with 0.1, 19 with 0.1, 20 with 0.2, or 21 with 0.6, and has dinner 7 (with 0.5) or 8 (with 0.5) hours after lunch. These facts can be modelled by the PTN:

where

The probabilistic quantitative temporal network (PQTN) in Example 1 can be graphically modelled as shown in Fig. 3.
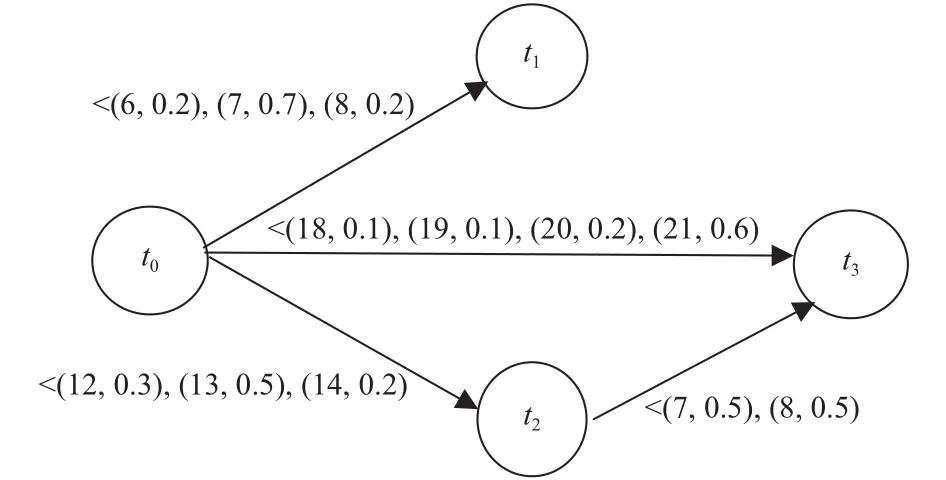
Fig. 3. Graphical representation of PQTN for Example 1.
4.Temporal Reasoning on PQTNs
Our representation model is basically an extension of the STP in order to include probabilities. We can thus perform temporal reasoning as in the STP, using Floyd-Warshall’s algorithm. However, we have to adapt it to applying to PQTNs. In order to achieve such a goal, we need to identify suitable definitions of the intersection ()and of the composition () operators, to propagate both distances and probabilities.
4.1 Intersection and Composition Operations
Now, we define our intersection and composition operators.For the sake of simplicity, we adopt the following notations.
Notations. Given two PQTLs c1and c2to be intersected or composed, we indicate withandwhich are the probabilities of d in the first PQTL and in the second PQTL,respectively.
In our approach, the operator intersectionis used in order to “merge” two constraintsconcerning the same pair of time points. The set intersection between the two input sets of distances is computed, and, for each intersecting distance, its probability is evaluated as the product of the probabilities of such a distance in the first and in the second constraints (since it is an “AND combination” of the two cases). The formal definition is given below.
Given two PTQLs:
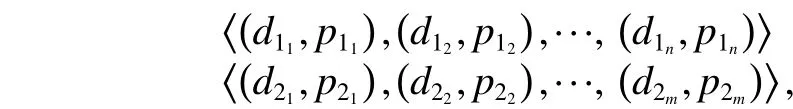
their intersection is defined as follows:

Notice that the intersectionmay be empty (in the case that the intersection betweenis empty).
Given two PTQLs
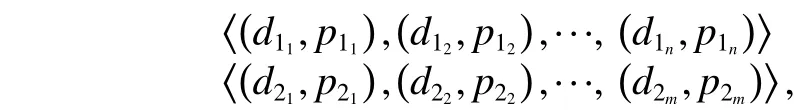
their composition is defined as follows:Let
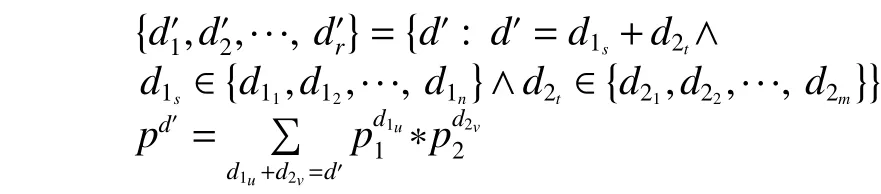
then
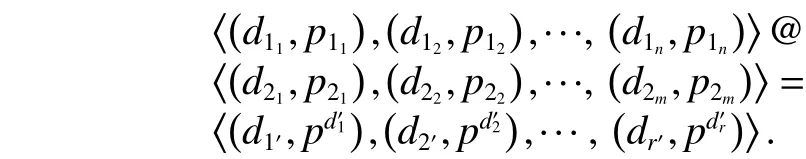
Example 2. As an example, let us consider the composition of the constraints between t0and t2and between t2and t3in Example 1:
As an example of intersection, let us intersect the above result with the constraint between t0and t3in Example 1, i.e.,

Complexity (intersection and composition). By exploiting the ordering of the distances, intersection can be computed in linear time and space (with respect to the number of distances).On the other hand, considering composition, the time required for the evaluation of the probabilities of the output distances is quadratic with respect to the number of input distances. As regarding space, given the fact that input (and output) distances are continuous, the number of output distances is the sum of the cardinality of the two sets of input distances.
4.2 Example
Example 3. The application of our instantiation of the Floyd-Warshall’s algorithm to the PTN in Example 1 gives as the result the set of constraintsin the following:

where

5.Query Answering
Temporal reasoning can be used in order to evaluate the minimal network of a set of PQTCs. To cope with the need of real applications and tasks/domains, however, having the minimal network is not enough. Indeed, it is very important to have the possibility of querying it, in order to see what the temporal constraints between specific time points are.Also, it is important to investigate the consequences of some assumption/choice, though queries of the form “what are the constraints between ··· if one assumes the constraints between ···” (this is very important, e.g., while adopting the widespread hypothesize and test paradigm). In our approach, we support several different types of queries. Part of our query language is reported in Fig. 4.

Fig. 4. Query language.
• Hypothetical queries (<HypQ>) are standard queries<StandardQ> that have to be answered with the assumption that some additional probabilistic temporal constraints (such a set of PQTCs is, indeed, a PTN, indicated by <PTN> in the grammar) hold.
Such queries are answered by first adding the new PQTCs to the minimal network, and then applying our instantiation of Floyd-Warshall’s algorithm to obtain a new minimal network. A warning is given in case no minimal network can be obtained, since the new constraints are not consistent with the given minimal network. Then, the query<StandardQ> is answered (as detailed below) in the new minimal network. Notice also that intersection () must be used in order to add the new hypothetical constraints.

and

The new constraints are then added to the minimal network(in substitution of the previous constraints between t1and t2and between t2and t3). Finally, the application of Floyd-Warshall’s algorithm to the resulting set of constraints provides the new minimal network as output:

The query <StandardQ> has to be answered considering such a network.
We distinguish among four types of standard queries.
1) Basic extraction queries (<BaseQList>) ask for the temporal distances (and their probabilities) between a list of pairs of time points. Such queries are trivially answered by reading the temporal constraints from the minimal network.
Example 5. For instance, given the minimal network in Example 3, the basic extraction queryasks for the temporal constraints (and their probabilities) between t0and t2,and between t0and t3, and gives as the result:
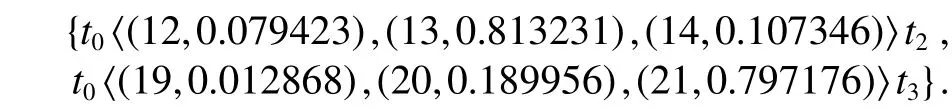
On the other hand, the hypothetical extraction queryasking what are the temporal constraints (and their probabilities) between t0and t2, and between t0and t3, in case the constraints in the “IF part” of the query are assumed, must be answered considering the minimal network described in Example 4, and gives as the result:

2) Individual probability (IP) queries provide as output the constraints in a PTN obtained by removing (from each constraint) all those pairs (d, p) such thatdoes not hold, whereis a comparison operator (i.e., one of <,≤, =, ≥, >), andis a probability value. Empty PQTCs are removed from the output. Notably, the result of such an operation is not a PTN, since, in the constraints, the sum of the probabilities is not necessarily 1.
Example 6. For instance, given the minimal network in Example 3, the query IP≥0.2 asks for those constraints which have a probability greater than 0.2, and gives as the result:

3) Global probability (GP) queries provide as the output the constraints obtained by first removing from the constraints all those pairs (d, p) such thatdoes not hold, whereis a comparison operator (i.e., one of <, ≤, =, ≥, >), andis a probability value. Empty PQTCs are removed from the output. Then, the resulting constraints are propagated, using our instantiation of Floyd-Warshall’s algorithm.
Example 7. For instance, given the minimal network in Example 3, the query “GP≥0.2” gives as the result:

4) Boolean queries (<BoolQ>) can be simple Boolean temporal queries (SBTQs) or composed Boolean temporal queries (CBTQs). Such queries ask about the validity of one(SBTQ) or more (CBTQ) constraints between pair of points,and return a Boolean value.
Definition. SBTQ and CBTQ.
An SBTQ is a query of the form:A CBTQ is a set of SBTQs.
Example 8. For instance, given the minimal network in Example 3, the queryasks whether 20 is a possible distance between t2and t3, and whether it has a probability greater or equal to 0.5. Given the above set of constraints, the result of the query is TRUE, since 20 is a possible distance between t2and t3, and the probability of the distance 20 is indeed 0.6, and thus greater than 0.5.
Answering a CBTQ is more complex. Indeed, it is not correct to separately test each SBTQ composing it, and returning TRUE if all checks are true (see the discussion in Section 2).
CBTQs are answered in four steps.
Step 1. Each SBTQ is checked independently of the others.If any one of them is not satisfied, a negative answer is provided. Otherwise, Steps 2 and 3 are performed.
Step 3. The resulting constraints are then propagated via the (instantiation of the) Floyd-Warshall’s algorithm.
Step 4. The answer is YES if the resulting set of constraint is consistent, NO otherwise.
Example 9. For instance, given the minimal network in Example 3, the result of Step 3 of the query(asking whether the distance between t0and t1may be 7, with the probability greater or equal to 0.5, and the distance between t2and t3may be 8, with the probability greater or equal to 0.5) is the following network:

so that the final answer is YES.
6.Conclusions
Many AI researches face the treatment of time and of temporal constraints. In order to cope with the need of many areas, including planning and scheduling, the current literature in the area is moving from the treatment of “crisp”temporal constraints to fuzzy or probabilistic constraints.Indeed, the recent literature shows that the treatment of probabilities and/or preferences in temporal reasoning is of paramount importance in the AI context. However, despite their wide use to cope with many tasks, probabilities have been studied only in conjunction with qualitative temporal constraints[30],[31], while they have not been proposed in combination with quantitative temporal constraints yet. This is a severe limitation in several areas, including planning and scheduling. In this paper, we overcome such a limitation by i)extending quantitative temporal constraints based on STP[6]with probabilities, and ii) proposing an approach for the propagation of such temporal constraints. Additionally,most applications require the possibility of asking queries to a set of temporal constraints. In this paper, to the best of our knowledge, iii) we propose the first approach supporting query answering on “non-crisp” (i.e., probabilistic)temporal constraints.
Though our approach is complete task and domain independent, in our future work we plan to apply it in the treatment of temporal constraints within the Guide-Line Acquisition, Representation and Execution (GLARE)[36]and META-GLARE[37]projects, to deal with clinical guidelines, and with their interactions[38].
[1]L. Vila, “A survey on temporal reasoning in artificial intelligence,”AI Communications, vol. 7, no. 1, pp. 4-28,1994.
[2]E. Schwalb and L. Vila, “Temporal constraints: A survey,”Constraints, vol. 3, no. 2, pp. 129-149, 1998.
[3]P. Terenziani, “Reasoning about time,” inEncyclopedia of Cognitive Science, London, vol. 3, 2003, pp. 869-874.
[4]J. F. Allen, “Maintaining knowledge about temporal intervals,”Communication of the ACM, vol. 26, no. 1, pp.832-843, 1983.
[5]M. Vilain and H. Kautz, “Constraint propagation algorithms for temporal reasoning,” inProc. of the 5th National Conf.on Artificial Intelligence, American Association for Artificial Intelligence, 1986, pp. 377-382.
[6]R. Dechter, I. Meiri, and J. Pearl, “Temporal constraint networks,”Artificial Intelligence, vol. 49, no. 1-3, pp. 61-95,1991.
[7]M. Koubarakis, “From local to global consistency in temporal constraint networks,”Theoretical Computer Science, vol. 173, no. 1, pp. 89-112, 1997.
[8]I. Meiri, “Combining qualitative and quantitative constraints in temporal reasoning,”Artificial Intelligence, vol. 87, no. 1-2, pp. 343-385, 1996.
[9]H. A. Kautz and P. B. Ladkin, “Integrating metric and qualitative temporal reasoning,” inProc. of the 9th National Conf. on Artificial Intelligence, 1991, pp. 241-246.
[10]D. Dubois, H. Fargier, and H. Prade, “Possibility theory in constraint satisfaction problems: Handling priority,preference and uncertainty,”Applied Intelligence, vol. 6, no.4, pp. 287-309, 1996.
[11]L. Godo and L. Vila, “Possibilistic temporal reasoning based on fuzzy temporal constraints,” inProc. of the 14th Intl.Joint Conf. on Artificial Intelligence, 1995, pp. 1916-1922.
[12]A. Bugarín, N. Marín, D. Sánchez, and G. Trivino, “Fuzzy knowledge representation for linguistic description of time series,” inProc. of the 16th Congress of the Intl. Fuzzy Systems Association, and the 9th Conf. of the European Society for Fuzzy Logic and Technology, 2015, pp. 1346-1353.
[13]S. Barro, R. Marin, J. Mira, and A. Paton, “A model and a language for the fuzzy representation and handling of time,”Fuzzy Sets and Systems, vol. 61, no. 2, pp. 153-175, 1994.
[14]L. Vila and L. Godo, “On fuzzy temporal constraint networks,”Mathware and Soft Computing, vol. 3, no. 91, pp.315-334, 1994.
[15]N. Kamide and D. Koizumi, “Method for combining paraconsistency and probability in temporal reasoning,”Journal of Advanced Computational Intelligence and Intelligent Informatics, vol. 20, no. 5, pp. 813-827, 2016.
[16]A. Gammoudi, A. Hadjali, and B. B. Yaghlane, “Modeling temporal relations between fuzzy time intervals: A disjunctive view,” inProc. of IEEE Intl. Conf. on Fuzzy Systems, 2016, pp. 50-57.
[17]C. Billiet, A. Bronselaer, and G. De Tré, “A comparison technique for ill-known time intervals,” inProc. of IEEE Intl.Conf. on Fuzzy Systems, 2016, pp. 1963-1969.
[18]T. Vidaland and H. Fargier, “Handling contingency in temporal constraint networks: From consistency to controllabilities,”Journal of Experimental and Theoretical Artificial Intelligence, vol. 11, no. 1, pp. 23-45, 1999.
[19]I. Tsamardinos, “A probabilistic approach to robust execution of temporal plans with uncertainty,” inProc. of the 2nd Hellenic Conf. on AI: Methods and Applications of Artificial Intelligence, 2002, pp. 97-108.
[20]R. Effinger, B. Williams, G. Kelly, and M. Sheehy,“Dynamic controllability of temporally-flexible reactive programs,” inProc. of the 19th Intl. Conf. on Automated Planning and Scheduling, 2009, pp. 19-23.
[21]K. B. Venable, M. Volpato, B. Peintner, and N. Yorke-Smith, “Weak and dynamic controllability of temporal problems with disjunctions and uncertainty,” inProc. of Workshop on Constraint Satisfaction Techniques for Planning and Scheduling, 2010, pp. 50-59.
[22]L. Hunsberger, R. Posenato, and C. Combi, “The dynamic controllability of conditional STNs with uncertainty,” inProc. of Planning and Plan Execution for Real-World Systems: Principles and Practices(PlanEx)Workshop, 2012,pp. 121-128.
[23]K. A. Jobczyk and A. Ligeza, “Towards a new convolutionbased approach to the specification of STPU-solutions,” inProc. of IEEE Intl. Conf. on Fuzzy Systems, 2016, pp. 782-789.
[24]P. H. R. Q. A. Santana and B. C. Williams, “Chanceconstrained consistency for probabilistic temporal plan networks,” inProc. of the 24th Intl. Conf. on Automated Planning and Scheduling, 2014, pp. 272-279.
[25]C. Fang, P. Yu, and B. C. Williams, “Chance-constrained probabilistic simple temporal problems,” inProc. of the 25th AAAI Conf. on Artificial Intelligence, 2014, pp. 2264-2270.
[26]N. Yorke-Smith, K. B. Venable, and F. Rossi, “Temporal reasoning with preferences and uncertainty,” inProc. of Intl.Joint Conf. on Artificial Intelligence, 2003, pp. 1385-1386.
[27]M. Li, H. Wang, C. Qi, and C. Zhou, “Handling temporal constraints with preferences in HTN planning for emergency decision-making,”Journal of Intelligent and Fuzzy Systems,vol. 30, no. 4, pp. 1881-1891, 2016.
[28]M. Mouhoub and A. Sukpan, “Managing temporal constraints with preferences,”Spatial Cognition and Computation, vol. 8, no. 1-2, pp. 131-149, 2008.
[29]M. D. Moffitt, “On the modelling and optimization of preferences in constraint-based temporal reasoning,”Artificial Intelligence, vol. 175, no. 7-8, pp. 1390-1409,2011.
[30]V. Ryabov and A. Trudel, “Probabilistic temporal interval networks,” inProc. of the 11th Intl. Symposium on Temporal Representation and Reasoning, 2004, pp. 64-67.
[31]M. Mouhoub and J. Liu, “Managing uncertain temporal relations using a probabilistic interval algebra,” inProc. of IEEE Intl. Conf. on Systems, Man and Cybernetics, 2008, pp.3399-3404.
[32]S. Badaloni and M. Giacomin, “The algebra IAfuz: A framework for qualitative fuzzy temporal reasoning,”Artificial Intelligence, vol. 170, no. 10, pp. 872-908, 2006.
[33]L. Khatib, P. Morris, R. Morris, and F. Rossi, “Temporal constraint reasoning with preferences,” inProc. of the 17th Intl. Conf. on Artificial Intelligence, 2001, pp. 322-327.
[34]P. Norvig and S. J. Russell, “Artificial intelligence: A modern approach,”Applied Mechanics & Materials, vol.263, no. 5, pp. 2829-2833, 1995.
[35]V. Brusoni, L. Console, and P. Terenziani, “On the computational complexity of querying bounds on differences constraints,”Artificial Intelligence, vol. 74, no. 2, pp. 367-379, 1995.
[36]P. Terenziani, G. Molino, and M. Torchio, “A modular approach for representing and executing clinical guidelines,”Artificial Intelligence in Medicine, vol. 23, no. 3, pp. 249-276, 2001.
[37]A. Bottrighi and P. Terenziani, “META-GLARE: A metasystem for defining your own computer interpretable guideline system-Architecture and acquisition,”Artificial Intelligence in Medicine, vol. 72, no. 1, pp. 22-41, 2016.
[38]L. Anselma, L. Piovesan, and P. Terenziani, “Temporal detection and analysis of guideline interactions,”Artificial Intelligence in Medicine, vol. 76, pp. 40-62, 2017, DOI:10.1016/j.artmed.2017.01.001
杂志排行
Journal of Electronic Science and Technology的其它文章
- Multi-Reconfigurable Band-Notched Coplanar Waveguide-Fed Slot Antenna
- Pairing-Free Certificateless Key-Insulated Encryption with Provable Security
- Overview of Graphene as Anode in Lithium-Ion Batteries
- High Power Highly Nonlinear Holey Fiber with Low Confinement Loss for Supercontinuum Light Sources
- Modeling TCP Incast Issue in Data Center Networks and an Adaptive Application-Layer Solution
- Message from JEST Editorial Committee
