Pairing-Free Certificateless Key-Insulated Encryption with Provable Security
2018-04-08LiBoHeDongJieYanHuXiongandZhiGuangQin
Li-Bo He, Dong-Jie Yan, Hu Xiong, and Zhi-Guang Qin
1.Introduction
1.1 Motivation
The first public key cryptography was proposed by Diffie and Hellman in 1976[1]. Nowadays the most popular public key cryptography RSA was presented by Rivest, Shamir, and Adleman in 1978[2], based on the definition of trapdoor oneway function. In the public key cryptosystem, a public key is used to encrypt the plaintext, meanwhile the corresponding private key is used to decrypt the associated ciphertext. To avoid the impersonate attack such as the public key replacement attack on the public key cryptography, public key infrastructure (PKI) as an authority is needed in public key encryption (PKE), the authority uses a certificate to bind the user and the user’s public key. The certificate is the signature generated by the authority PKI. The PKI has a very complicated infrastructure for the certificate management including the storage, distribution, revocation, and verification of the certificate. So the PKI has difficulty in the efficiency and scalability.
A encryption scheme, identity based encryption (IBE), was introduced by Shamir in 1984[3]. This encryption solves the problem of authenticity for the public key by informing a public key directly from the user’s identity. In the IBE scheme, key generation center (KGC) generates the private key for a user and the system parameters including the master key. The master key and the user’s entity are combined to form a private key. Thus, the IBE scheme meets a challenge, the problem of the key escrow. If the KGC is malicious, it will know the master key. As a result,the private key will be exposed and the security of the entire cryptosystem will be compromised.
To solve the above problem, the certificateless public key encryption (CL-PKE) was proposed by Al-Riyami and Paterson in 2003[4]. In this new kind of encryption, Al-Riyami and Paterson added a new component into the private key,secret value, which is generated by a user himself and also kept by the user himself. So even if the malicious KGC leaks the partial part of the private key created by KGC, the attacker also cannot get the entire private key to decrypt the associated ciphertext. Through this, the problem of key exposure is alleviated and the security of the cryptosystem is maintained.
However, we will always meet a more complicated and hostile environment where the private key may be exposed in a higher risk. In order to solve these challenges in practice, He et al.[5]proposed a certificateless key-insulated encryption(CL-KIE) scheme which integrated the key-insulated security notion into the CL-PKE scheme. The key-insulated security notion was denoted by Hea, Dodis, and Rabin in 2002[6]. In this new security notion, the time is divided into n time periods. A physical secure device generates a helper key in the cryptosystem during each time period and keeps the helper key secret from KGC. The private key consists of a partial private key generated by KGC and a periodically updated helper key.So even if the private key is leaked in a time period, the security of the whole cryptosystem will not be affected in next time periods. Through this approach, we can efficiently alleviate the cryptosystem disaster led by temporary private key exposure. A number of key-insulated schemes[7]-[11]have been proposed. Following their work, here we propose a CL-KIE scheme which is composed of the key-insulated security notion and the CL-KIE scheme. The proposed CL-KIE scheme can provide higher security protection in practical environments.
The CL-KIE scheme proposed by He et al.[5]is based on bilinear pairing. The efficiency of the bilinear pairing computational operation is much lower compared with other computational operations such as the modular exponentiation in finite fields[12]. To overcome this, a lot of work[13],[14]has been conducted to increase the computational performance of encryption schemes. In this paper, we want to propose another scheme which not only can alleviate the problem of key exposure in the practical hostile environment but also can achieve higher computational efficiency.
1.2 Contribution
In this paper, we proposed a scheme called paring-free CL-KIE scheme. First, we formalize the definition of the scheme and construct its security model. Then we give the concrete construction of the proposed scheme. We also prove the security of the proposed scheme against the chosen plaintext attacks (CPAs) in the random oracle model considering the assumption of the computational Diffie-Hellman (CDH) hardness problem. Finally, we compare our scheme with CL-PKE[4]and the CL-KIE[5]in order to show the advantages of our scheme both on security and efficiency.
2.Definition
In this section, we first formalize the definition of CL-KIE and give its security model. Then we introduce the related hardness problem assumption which the security of the scheme is based on.
2.1 Formal Definition
The CL-KIE scheme consists of the following eight algorithms:
1) Setup: This is a probabilistic algorithm performed by a KGC that accepts a security parameterto generate system parameters params, a master key, and a helper key.
2) SetSecretValue: This is a probabilistic algorithm performed by a user that accepts system parameters params and an identity stringto generate a secret value.
3) HelperKeyUpdate: This is a deterministic algorithm performed by a secure physical device that accepts system parameters params, a helper key, an identity string ID, and a time period i to generate a helper private key.
4) PartialKeyExtract: This is a probabilistic algorithm performed by a KGC that accepts system parameters params, a master key, an identity string, and a time period i to generate a partial public keyand a partial private key.
5) SetPublicKey: This is a deterministic algorithm performed by a user that accepts system parameters params, the secret value, and the partial public keyto generate a public key.
6) SetSecretKey: This is a deterministic algorithm performed by a user that accepts system parameters params, the secret value, and the partial private keyto generate a private key.
7) Encrypt: This is a probabilistic algorithm performed by a sender that accepts system parameters params, the plaintextat a time period i, the user’s identity string ID, and the public keyto generate the corresponding ciphertext.
8) Decrypt: This is a deterministic algorithm performed by a receiver that accepts system parameters params, the ciphertextat a time period i , the user’s identity string, and the private keyto get the plaintextor “Reject”.
2.2 Security Model
The same as the pairing-free CL-PKE scheme proposed by Baek, Safavi-Naini, and Susilo[13], the user in our scheme also needs to interact with KGC and authenticate himself to KGC to get a partial public key which is used to generate a full public key. The partial output of the algorithm PartialKeyExtract is the input of the algorithm SetPublicKey. Especially in our scheme,the user needs to interact with a secure physical device to get a helper key which is also an important component of the full private key. The output of the algorithm HelperKeyUpdate is the input of the algorithm SetPublicKey. In our scheme, we consider two types of adversaries Type I adversary () and Type II adversary ():represents the external attacker who cannot access the master key but can replace the public key for an entity with its choice;represents the malicious KGC who can access the master key but cannot replace the public key by itself. We model the security of our scheme through two games (Game 1 and Game 2) where a challenger interacts with an adversary (and) and a challenger.
First, we list the random oracles may be issued in our games as follows:
1) Partial-Key-Extract: On accepting system parameters params, a master key, an identity string, and a time period i,the challengerruns the algorithm PartialKeyExtract to generate a partial public keyand a partial private key,then sends these results to the adversary.
2) Helper-Key-Update: On accepting system parameters params, a helper key, an identity string, and a time period i,the challengerruns the algorithm HelperKeyUpdate to generate a helper private key, then returnsto the adversary.
3) Private-Key-Request: On accepting system parameters params, the secret value, and the partial private key, the challengerruns the algorithm SetSecretKey to generate a private key, then sends this private keyto the adversary.
4) Public-Key-Request: On accepting system parameters params, the secret value, and the partial public key, the challengerruns the algorithm SetPublicKey to generate a public key, then sends this public keyto the adversary.
5) Public-Key-Replace: The adversarycan repeatedly replace the public key for any entity with any value on’s choice at any point.
6) Set-Secret-Value: On receiving system parameter params and an identity string, the challengerruns the algorithm SetSecretValue, then sends the secret value z to the adversary.
i) Game 1: Choosing plaintext security of CL-KIE for.
Guess: Finally, the adversaryguesses a bit,then the adversarywill win the game if.
There are a few restrictions onas follows:
Guess: Finally, the adversaryguesses a bitthen the adversarywill win the game if.
There are a few restrictions onas follows:
2.3 CDH Assumption
The security of our scheme is based on CDH assumption.
The CDH assumption states that a certain computational problem within a cyclic group is hard. Letandbe primes such thatgivingfor a randomly chosen generatorand random, it is computationally intractable to compute the valuein,wheredenotes the multiplicative group whose order is;denotes the multiplicative group whose order is.
3.Construction
Now we give the concrete construction of the pairing-free CL-KIE scheme.
Select four cryptographic hash functions:and, where, anddenotes the natural number set;denotes the positive integer set; l,, anddenote three integers.
The system parameters are params=, master key=x, and helper key=.
• HelperKeyUpdate(i , params, helper key,): Given params, a helper key, and an identity string ID at the time period, the algorithm periodically generates a helper private key, and returnsas the user’s helper private key.
• PartialKeyExtract(i, params, master key, ID): Given params, a master key, and an identity string ID at the time period, the algorithm uniformly selects anand computesas the partial public key, then the algorithm generates the corresponding partial pivate keyLet DID=t, return
The structure of the CL-KIE scheme is given in Fig. 1.

Fig. 1. Structure of the CL-KIE scheme.
4.Analysis
4.1 Security Proof
Proof. Suppose that there is a Type I adversary, who presents an external attacker who knows the secret valueand cannot get a master key. Given a random instance,we construct a CDH attackerto compute the value ofto break the CDH assumption by making use of. Now we give the concrete proof as follows.
6) Public-Key-Replace: On receving the Public-Key-Replace query onreplaces the tuple on PublicKeyList forwith the new tuple
[Analysis] When the game begins, the CDH attackersetsand simulates hash functions as random oracles. Then the CDH attacker sends params=to. During the simulation,needs to guess every bit in the target plaintextwith the target identity stringin a time period. The CDH attackerwill set, andwhere the CDH attacker(noted thatdoes not know) andWe evaluate the simulation of the decryption oracle. The CDH attackerreturns the target ciphertextWe can get:
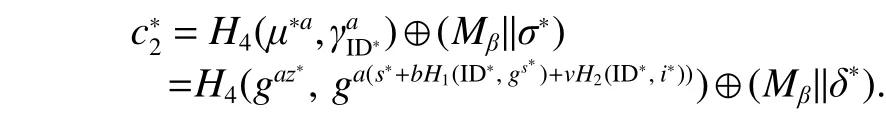
Furthermore
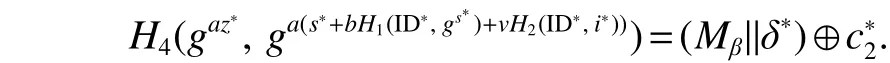
According to the equation above, given the values of,and, it is easy to compute. The CDH attackercan get the solution of the CDH problem. Through this reduction, we can prove the security of our scheme against Type I adversary on indistinguishability under chosen plaintext attacks(IND-CPAs).
Proof. Suppose that there is a Type II adversary, who presents a malicious KGC who cannot get the secret value generated by user himself. Given a random instance, and, we construct a CDH attackerto compute the value ofto break the CDH assumption by making use of. Now we give the concrete proof as follows:
2) Public-Key-Request: B maintains a list PublicKeyList of tuplewhich is initially empty. Whenissues a query on,responds as follows:
[Analysis] When the game begins, the CDH attackersimulates hash functions as random oracles. Then the CDH attacker sends params=to.During the simulation,needs to guess every bit in the target plaintextwith the target identity stringin a time period. The CDH attacker will setwhich keeps secret by user himself. The CDH attackeralso will setwhere the CDH attacker sets(noted thatdoes not know),We evaluate the simulation of the decryption oracle. The CDH attackerreturns a target ciphertext. We can get:

According to the equation above, given the values of, it is easy to compute. Thus the CDH attackercan get the solution to the CDH problem. Through this reduction, we can prove the security of our scheme against Type II adversary on IND-CPAs.
4.2 Performance Comparison
In this section, we will compare the performance of our scheme with the certificateless public key cryptography presented by Al-Riyami and Paterson[4]and the CL-KIE on bilinear pairing proposed in He et al.[5]in Table 1. We assume the two schemes are based on bilinear pairing and implemented onbits andbits (anddenote two cyclic groups). Our pairing-free CL-KIE scheme is implemented onandwhereandare both 1024-bit length primes and satisfying the condition that q|p−1. For the other system parameters, we set=160 bits,=160 bits, and Hash function=160 bits. Then, we list the costly computational operations. We denote the point multiplication inby, the exponentiation inby, the pairing computation byand the exponentiations inandby. We omit the other trivial computational operations.

Table 1: Performance comparison
Depending on a 512-bit Tate pairing takes 20.0 ms whereas a 1024-bit prime modular exponentiation takes 8.8 ms in the multiprecision integer and rational arithmetic C/C++ library(MIRACL) implementation[12], the computational performance of pairing is more expensive than it of modular exponentiation in finite fields. So the computation of our scheme is more efficient in every phase among PartialKeyExtract,SetPublicKey, Encrypt, and Decrypt compared with the other two schemes. A periodically updated helper key in the private key of our scheme can provide an extra security capability that can alleviate the problem of private key leakage, as compared with CL-PKE scheme[4]. Our paring-free CL-KIE scheme also can achieve the same security requirement as that of the CL-PKE[6]. Above all, our paring-free CL-KIE is optimal both on efficiency and security among the three schemes in Table 1.
4.3 Potential Application
Our scheme can be applied to a lot of applications which meet the key escrow problem. For instance, a common server can be used to store the private data for personal, meanwhile the common server can communicate with the mobile phone of every user. The mobile phone of every user can periodically generate a helper key which will be one component of the private key. So the private key will be updated at every time period. Assuming this situation, a malicious friend of one user Bob, who knows Bob’s secret value, breaks the KGC on the server to know the master key of the cryptosystem. Even in this case, this malicious friend still cannot get the valid private key of Bob to decrypt his personal data. Above all, our CL-KIE scheme can provide high security protection for the privacy-sensitive environment.
5.Conclusions
In order to increase the efficiency of CL-KIE and achieve the security requirement that mitigates the key exposure, in this paper, we proposed a pairing-free CL-KIE scheme which combines the key-insulated security notion and the CL-KIE scheme. First, we formalized the definition of pairing-free CL-KIE scheme and constructed the security model of our scheme. Then, we gave the concrete construction of the pairing-free CL-KIE scheme. After that, we proved the security of our scheme against the IND-CPAs under random oracles considering the assumption of the CDH problem. Finally, we compared our scheme with the CL-PKE[4]and CL-KIE[6]on efficiency and security. It is observed that, the proposed pairing-free CL-KIE scheme is optimal because our scheme not only can reduce a lot of the computational running time but also can achieve key-escrow and key-exposure resiliences. In the future, we plan to construct more schemes to avoid the problem of key escrow and give the security proof in the standard model to meet the high security requirement in the complicated practical environment.
Acknowledgment
We would like to thank the referees for their valuable suggestions.
[1]W. Diffie and M. E. Hellman, “New directions in cryptography,”IEEE Trans. on Information Theory, vol. 22,no. 6, pp. 644-654, 1976.
[2]R. L. Ronald, A. Shamir, and L. Adleman, “A method for obtaining digital signatures and public-key cryptosystems,”Communications of the ACM, vol. 21, no. 2, pp. 120-126,1978.
[3]A. Shamir, “Identity-based cryptosystems and signature schemes,” inProc. of the Workshop on the Theory &Application of Cryptographic Techniques, 1984, pp. 47-53.
[4]S. S. Al-Riyami and K. G. Paterson, “Certificateless public key cryptography,” inProc. of Intl. Conf. on the Theory and Application of Cryptology and Information Security, 2003,pp. 452-473.
[5]L. He, Y. Chen, H. Xiong, and Z. Guang, “Certificateless key insulated encryption: Cryptographic primitive for achieving key-escrow free and key-exposure resilience,” inProc. of Intl. Conf. on Big Data Computing and Communications,2016, pp. 387-395.
[6]A. J. Hea, Y. Dodis, and T. Rabin, “On the security of joint signature and encryption,” inProc. of Intl. Conf. on the Theory and Applications of Cryptographic Techniques, 2002,pp. 83-107.
[7]H. Hong and Z. Sun, “High efficient key insulated attribute based encryption scheme without bilinear pairing operations,”Springer Plus, vol. 5, no. 1, pp. 1-12, 2016.
[8]Z. Wan, J. Li, and X. Hong, “Parallel key-insulated signature scheme without random oracles,”Journalof Communications and Networks, vol. 15, no. 3, pp. 252-257,2013.
[9]R. Sreenivasa and R. Dutta, “Attribute-based key-insulated signature for boolean formula,”Intl. Journal of Computer Mathematics, vol. 93, no. 6, pp. 1-25, 2015.
[10]P. Gopal and P. Reddy, “Efficient ID-based key-insulated signature scheme with batch verifications using bilinear pairings over elliptic curves,”Journal of Discrete Mathematical Sciences and Cryptography, vol. 18, no. 4, pp.385-402, 2015.
[11]Y. Chen, W. Xu, and H. Xiong, “Strongly secure certificateless key-insulated signature secure in the standard model,”Annals of Telecommunications, vol. 70, no. 9-10, pp.395-405, 2015.
[12]MIRACL, Multiprecision integer and rational arithmetic C/C++ library. [Online]. Available: http://indigo.ie/mscott/
[13]J. Baek, R. Safavi-Naini, and W. Susilo, “Certificateless public key encryption without pairing,” inProc. of Intl. Conf.on Information Security, 2005, pp. 134-148.
[14]J. Lai, W. Kou, and K. Chen, “Self-generated-certificate public key encryption without pairing and its application,” inProc. of Intl. Conf. on Practice and Theory in Public-Key Cryptography, 2007, pp. 476-489.
杂志排行
Journal of Electronic Science and Technology的其它文章
- Message from JEST Editorial Committee
- Modeling TCP Incast Issue in Data Center Networks and an Adaptive Application-Layer Solution
- UEs Power Reduction Evolution with Adaptive Mechanism over LTE Wireless Networks
- Multi-Reconfigurable Band-Notched Coplanar Waveguide-Fed Slot Antenna
- High Power Highly Nonlinear Holey Fiber with Low Confinement Loss for Supercontinuum Light Sources
- Overview of Graphene as Anode in Lithium-Ion Batteries
