Simulating Eastern-and Central-Pacific Type ENSO Using a Sim p le Coup led M odel

Xianghui FANG and Fei ZHENG

1Institute of Atmospheric Sciences,Fudan University,Shanghai 200438,China

2International Center for Climate and Environment Science(ICCES),Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China

3Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters,Nanjing University of Information Science and Technology,Nanjing 210044,China

1.　Introduction

As the concept of central Pacific(CP)El Nio began to emerge(Fu and Fletcher,1985;Larkin and Harrison,2005;Ashok et al.,2007;Yu and Kao,2007;Kao and Yu,2009;Kim et al.,2009;Kug et al.,2009),comparisons between this new type and the traditional eastern Pacific(EP)type of ENSO(El Nio–Southern Oscillation)were intensively conducted,including the triggering factors(Vimont et al.,2001,2003;Kug et al.,2009;Lee and McPhaden,2010;Yu and Kim,2011;Ham et al.,2013),the occurrence frequency(Kug et al.,2009;Lee and M cPhaden,2010),the amplitude(e.g.,Zheng et al.,2014),the dynam ic mechanisms(Kug et al.,2009;Yu et al.,2010),the predictabilities(e.g.,Zheng and Yu,2017),and the impacts on the global climate(Kumar et al.,2006;Feng and Li,2011;Zhang et al.,2011).On the subject of the dynamic mechanisms,due to the fact that the anomalous warming center of EP ENSO is located in the EP,the mean thermocline(TH)is quite shallow and permits the perturbations on the subsurface to effectively influenc the sea surface temperature(SST)through upwelling processes,including both TH and Ekman(EK)feedback.In contrast,for CP ENSO,the major warming center is concentrated in the CP,where the TH is relatively deep.This means that the upwelling processes have less of an impact on the SST.However,because the zonal mean SST gradient is strongest in this region—due to the warm pool to the west and the cold tongue to the east—the anomalous zonal-current-related zonal advective(ZA)feedback plays the dominant role.The relative contributions of the TH,EK and ZA processes in the equatorial Pacific have also been widely diagnosed using observational datasets(Latif,1987;K leeman,1993;Kug et al.,2009).

From another perspective,although ENSO is regarded as a kind of recurring event,with the positive phase named El Nio and the negative phase La Nia,many asymmetries exist between these two phases(Burgers and Stephenson,1999;Jinetal.,2003;Su et al.,2010;Sun and Zhang,2006).Forexample,El Nio is always stronger than La Nia;the anomalous cooling center during La Nia is located relatively farther west than during El Nio;and the decaying period of La Nia is longer than that of El Nio.Although many studies have investigated the differences between the two types of ENSO and the asymmetries between the two phases of ENSO,and have obtained certain results,it is still a great challenge for general circulation models(GCMs)to successfully simulate these ENSO characteristics.

Because GCMs include many factors that can influenc ENSO events,it is not always easy to quantify the feedback contributions or to attribute the main defects to the correct causes.For this reason,simple models consisting of only the major processes that influenc ENSO are always good candidates for studying specific problems or mechanisms.In this study,a linear air–sea coupled model of the equatorial Pacific is utilized to investigate the importance of the major dynam ic mechanisms(e.g.,the TH,EK and ZA feedbacks)on the ENSO problems mentioned above.

The rest of this paper is organized as follows:Section 2 gives a brief description of the data and the simple model used in this study.Section 3 describes the modification of the model and its ability to simulate the traditional EP type of ENSO.Section 4 tests the influenc of the ZA feedback on simulating the CP type of ENSO.In Section 5,using a simple nonlinear control scheme,the characteristics of the two types of El Nio are simultaneously simulated,as well as the asymmetries between the two phases of the ENSO events.The results are summarized and discussed in section 6.

2.　Datasets,methods and model

2.1.　Datasets and methods

Observational and reanalysis datasets are used to analyze the developing phase of El Nio.The wind stress data are from NCEP Reanalysis-2(Kanamitsu et al.,2002);the SST data are from ERSST.v3b(Smith et al.,2008);and the monthly ocean temperature and oceanic circulation data are from GODAS(Behringer and Xue,2004).They are used to quantify the contributions of each oceanic feedback process on the development of the SST and calculate the TH depth(TCD—indicated by the 20°C isotherm depth).The analysis period is from 1980 to 2010.Anomalies presented in this study are calculated by removing the monthly mean climatology.Following Xiang et al.(2013), fiveCPElNio(1991/92,1994/95,2002/03,2004/05and 2009/10)and four EPElNio events(1982/83,1986/87,1997/98 and 2006/07)are chosen.The developing phase for each event is defined as from the month when the oceanic Nio index becomes larger than 0.5°C until the end of the calendar year.For example,the developing phase is from June to December for the 1991/92 El Nio event,and from May to December for the 1997/98 El Nio event.

To measure the relative contributions of each oceanic feedback on the development of the SST,a straightforward method is used to conduct a budget analysis of the mixed layer temperature.The temperature equation is as follows:

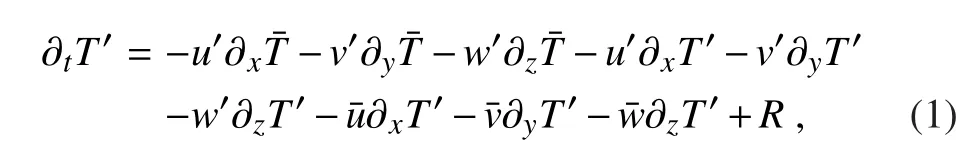
where overbars and primes represent the monthly climatology and anomaly,respectively.The variablesu,vandTare the zonal and meridional currents and oceanic temperature averaged over the mixed layer.The vertical velocity(w)is measured at the bottom of the mixed layer.Ris the residual term,which consists of thermodynamic processes and influences from variation other than that on the interannual time scale,amongst other factors.This method is the same as that used in Kug et al.(2009).

Fig.1.　(a)Observational linear contributions of ZA(black line and gray shading),TH(blue line and shading),EK(green line and shading),and the combination of TH and EK(red line and shading)feedbacks to the SST tendency along the equatorial Pacific.(b)Factors in the SST equations,Eqs.(2)and(3),as a function of longitude;here,α is in units of K(10 m)−1 month−1,β in K(0.1 Pa)−1 month−1,and γ in month−1.

Figure 1a illustrates the relative contributions of each process[rhs of Eq.(1)]to the development of local SST tendencies[lhs of Eq.(1)]in the equatorial Pacific for the whole period(1980–2010),rather than for specific El Nio events,as calculated in Kug et al.(2009).It indicates that the ZA feedback(i.e.,the anomalous zonal current and mean zonal tem-perature gradient—black line in the figure)plays the dominant role in the CP region,where the largest mean zonal temperature gradient is located.In the western and eastern areas,the contribution from the ZA feedback is relatively weak.Instead,the TH feedback(i.e.,the mean vertical velocity and anomalous vertical temperature gradient—blue line)and the EK feedback(i.e.,the anomalous vertical velocity and mean vertical temperature gradient—green line)processes are dominant.Specifically,the TH feedback plays an important role in the central–eastern region,i.e.,110°–150°W,with a comparable contribution to the ZA feedback,and the EK feedback plays the dominant role in the eastern part of the Pacific,i.e.,80°–110°W.Because the TH and EK feedbacks are both related to vertical upwelling processes,their combined effects are also illustrated in Fig.1a(red line).It shows that the total vertical upwelling processes can explain the majority of the SST development over the central–eastern Pacific region,with the relative contribution exhibiting a near linear increase from the central to the eastern area.Meanwhile,these feedbacks have nearly no effect upon the far western Pacific(WP),where the mean TH is too deep and the zonal mean SST gradient is too small.The contributions from the other oceanic processes in Eq.(1)are very small,so they are not shown in the figure.Overall,this observational analysis indicates that the ZA feedback(a parabolic shape with maximal strength located in the CP)and the vertical upwelling processes(a near linear increase in strength from the CP to EP)play the dominant roles in the development of the SST in the CP and central–eastern Pacific,respectively.

2.2.　Model

A linear air–sea coupled model of the equatorial Pacific(GMODEL V3.0)is used in this study(Burgers et al.,2002;Burgers and Van Oldenborgh,2003),which can be obtained at http://www.sciamachy-validation.org/research/CKO/gmodel.htm l.Its oceanic dynamic component is a wind-forced linear shallow water(“1.5 layer”)model of a baroclinic mode on a beta plane.

The atmospheric model comprises simple bivariate linear regression patterns of observed wind stress anomalies to observed SST anomalies in the Nio3(5°S–5°N,90°–150°W)and Nio4(5°S–5°N,160°E–150°W)regions(Burgers and Van Oldenborgh,2003),based on the reality that these two fields are coupled quite well in the equatorial Pacific region.These regression patterns are then combined with noise and used during the run to calculate the likely atmospheric response to model SST anomalies.Details can be found in Burgers and Van Oldenborgh(2003)and Fang and Zheng(2014).

Given the response of SST to TH depth and wind stress anomalies,the SST model(Burgers and Van Oldenborgh,2003)is valid only in the central and eastern equatorial Pacific,i.e.,

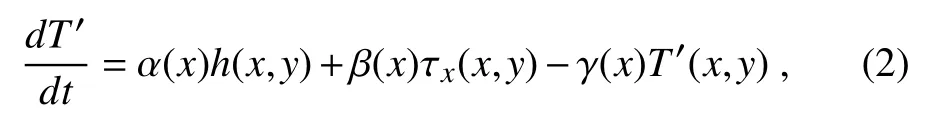
where the factors α,β and γ determine the strength of the TH feedback(i.e.,the term proportional to the anomalous TCDh),zonal wind stress feedback(i.e.,the term proportional to the anomalous zonal wind stress τx),and the relaxation term(i.e.,the term proportional to the anomalous SSTT′),which vary considerably along the equator(Fig.1b).It can be seen,in the EP,that the SST tendency is linearly related to the TH depth anomaly,with the coefficient depending on longitude and becoming stronger in the EP(dotted line in Fig.1b).Comparing with the observation in Fig.1a,this distribution bears a strong resemblance to the vertical upwelling processes(red line),which means the TH feedback defined in the model actually contains both the TH and EK feedbacks.In the CP,where the ZA feedback dominates,a term proportional to the anomalous zonal wind stress,but not the zonal current,is used in the SST equation.As stated by Burgers and Van Oldenborgh(2003),the disadvantage of this setting is that the zonal velocity fluctuations that are not related to local zonal wind stress variations are not taken into account.The zonal wind stress feedback is not equivalent to the ZA feedback.Comparing with Fig.1a,the distribution of this coefficient(dashed line in Fig.1b)also bears a strong resemblance to the observational linear contribution of the ZA feedback to the SST development(black line).These comparisons indicate that the simple modeling of the major processes influencing the SST development is quite reasonable.In addition,the strength of the linear damping processes in the SST equation is also shown by the solid line in Fig.1b.

In the simulations,external noise in the form of wind stress variations forces the oceanic shallow water model and induces the variation of the TH depth.The TH depth and zonal wind stress anomalies influenc the SST through the TH and wind stress feedbacks.The varied SST in turn impacts the zonal wind stress anomalies through the atmospheric model,and so on.Details of the model description and its performance when simulating ENSO can be found in related articles(Burgers et al.,2002;Burgers and Van Oldenborgh,2003;Philip and Van Oldenborgh,2010;Fang and Zheng,2014;Zhang et al.,2015;Zheng et al.,2015).In this study,each experiment conducted in GMODEL lasts for 100 years,and the analyzed period is the final 50 years.

3.　Modification of GMODEL and its performance

3.1.　Modifying GMODEL to GMODEL-ZA

As mentioned above,many observational analyses have indicated that the ZA feedback is the dominant dynamic process for the development of CP ENSO.However,GMODEL does not directly represent this term,but instead utilizes a socalled wind stress feedback.To better depict the ZA feedback and measure its impact on the ENSO events,the wind stress feedback must be modified into the correct ZA feedback,which linearly correlates with the zonal current anomaly[i.e.,uin Eq.(3)],but not the zonal wind stress anomaly,i.e.,

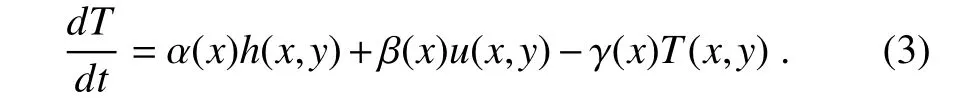
The feedback strength distribution remains due to its strong resemblance to the observations.To distinguish from the original GMODEL,the modified GMODEL is termed GMODEL-ZA.

3.2.　Performance of GMODEL-ZA when simulating ENSO events

As a linear air–sea coupled model,the simulated ENSO pattern is quite unique.For this reason,and for achieving results that are more physically consistent,the method of combined empirical orthogonal function(CEOF)analysis is a straightforward way to exhibit the distribution of the simulated ENSO phenomenon.Figure 2 shows the leading CEOF patterns of the anomalous SST,zonal wind stress(Taux),and TCD of the 51st–100th model years simulated by GMODELZA,which is termed the CTRL run.Also,the observational composites of the anomalous SST,Taux and TCD during the developing phase of EP El Nio are illustrated in the righthand panels.It can be seen that the patterns of the three fields are strongly coupled together and exhibit typical EP ENSO patterns,i.e.,from the perspective of the positive phase,the major warming occurs in the EP,while the cooling part shows a lateral V-shape with the corner located in the west;the strong westerlies are mainly located in the CP and WP,while the weak easterlies are located in the EP and far WP;the TCD pattern is similar to that of the SST,with the TCD deepening in the EP while shallowing in the west.As the TCD feedback is much stronger in the EP than in the WP,the SST variation in the WP is relatively weak,although the local TCD variation is intense.The patterns of TCD and Taux are tightly linked by the Sverdrup balance,i.e.,the balance between the zonal wind stress and the TH depth tilt along the equator(Jin,1997).This indicates GMODEL-ZA can capture the major patterns of EP ENSO successfully,as well as the coupled relationships among the air–sea fields.

Fig.2.　Leading CEOF patterns of the 51st–100th model years simulated by the CTRL run(left-hand panels)and the observational composites of the developing phase of EP El Nio(right-hand panels)for(a,b)SST,(c,d)Taux and(e,f)TCD.The numbers at the top of(a)indicate the percentage of variance explained by the CEOF mode.Contour intervals for(a–f)are 0.4°C,0.4°C,0.01 N m−2,0.004 N m−2,10 m,and 10 m,respectively.Purple dashed lines in each panel are along the equator and dateline.

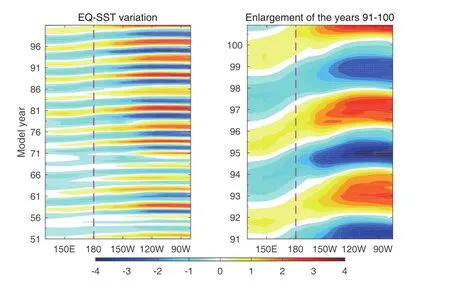
Fig.3.　Time–longitude diagrams of the monthly SST anomalies in the equatorial Pacific during the 51st–100th(left)and 91st–100th(right)model years simulated by the CTRL run.Purple dashed line in each panel is along the dateline.

To depict the variation of the ENSO system,Fig.3a shows a time–longitude diagram for monthly SST anomalies along the equator,with the last 10 years(91–100)enlarged in Fig.3b.SST anomalies consistently propagate eastward,with the amplitude small in the west and gradually amplifying from the CP to the east under the combined effects of the ZA and TH feedbacks.This is the typical variation of the traditional EP type of ENSO,as indicated by both delayed oscillation and recharge oscillation.Calculating the power spectrum of the Nio3.4(5°S–5°N,120°–170°W)SST index,the major period of this CTRL run is 4.04 years,which is consistent with observations(Kao and Yu,2009).This experiment indicates that GMODEL-ZA can capture the main characteristics of EP ENSO reasonably well,reflecting that the standard TH feedback is much stronger than the ZA feedback in influencing the SST development.However,being a linear model,it can only simulate a unique pattern,which means it cannot simulate the CP ENSO or the asymmetries between El Nio and La Nia.

4.　Simulating CP ENSO in GMODEL-ZA

Observational analyses have indicated that the occurrence and development of CP ENSO are mainly concentrated in the CP region,where the TCD is too deep to effectively impact the SST development.Instead,the ZA feedback related to the mean zonal SST gradient and anomalous zonal current plays the dominant role.As a result,if the TH feedback is not weakened in the model,even though the original warming center occurs in the CP,the SST in the EP will grow to be higher than that in the CP during the developing period and will make the event into an EP type eventually,due to the TH feedback being much stronger than the ZA feedback.Thus,to solely simulate the characteristics of CP ENSO,the TH feedback in GMODEL-ZA is switched off[i.e.the first term on the rhs of Eq.(3)is removed].This experiment is termed the CP ENSO run.

Figure 4 shows the leading CEOF patterns of the anomalous SST,Taux and TCD of the51st–100thmodel years simulated in the CP ENSO run,along with the observational composites during the developing phase of CP El Nio illustrated in the right-hand panels.It indicates that the patterns are totally different from those of the CTRL run.From the perspective of the positive phase,the major warming center is situated in the CP while the weaker warming occurs in the eastern region;the corresponding westerly wind stress anomalies are also in the CP and WP,with a significant westward shift compared with the CTRL run,and the easterlies in the EP have a larger zonal stretch and amplitude.These results are consistent with the observations.The TCD anomalies still show a west-shallow ing–east-deepening pattern,but the positive TCD anomalies show a westward shift and are located in the CP and EP,while negative anomalies are limited to the west and have a narrower zonal stretch.The patterns of TCD and Taux are also tightly linked by the Sverdrup balance,with a consistently westward shift.This indicates that,after sw itching offthe TH feedback and only retaining the ZA feedback and the damping term,the air–sea interaction of the equatorial Pacific can induce the major patterns of CP ENSO reasonably well.

Fig.4.　As in Fig.2 but for the results simulated by the CP ENSO run.

Figure 5a shows the time–longitude diagram for monthly SST anomalies along the equator,with the last 10 years(91–100)enlarged in Fig.5b.The major SST anomalies are mainly located in the CP,with an eastward propagation from the west to the CP,but no significant eastward propagation from the CP to the east.This manifests the characteristic local development of CP ENSO.It also shows that CP ENSO is much weaker than the EP type,due to the weaker strength of the ZA feedback compared with that of the TH feedback.The power spectrum of the Nio3.4 SST index shows that the major period of this CP ENSO run is concentrated in 2–3 years,with 2.7 years being the most significant.This is also consistent with observations(Kao and Yu,2009).It should be noted that,in the model,due to the TH(ZA)feedback mainly dominating the EP(CP),the Taux center is located in the CP and WP(more to the latter).Therefore,the balance relative to the Taux is maintained by the TCD anomalies between the WP and EP(CP).The system will take a longer(shorter)time to propagate the signal between the two regions via Kelvin and Ross by waves,producing a longer(shorter)period.The relative role of the ZA and TH feedbacks in shaping the characteristics of ENSO(including period and propagation orientation)was also investigated by Zhu et al.(2011).Their study mentioned that the more important the role played by the ZA feedback,the higher frequency oscillations would be observed,which is consistent with the results obtained here.

This experiment indicates that GMODEL-ZA without TH feedback can capture the main characteristics of CP ENSO reasonably well,confirming the dominant role played by the ZA feedback.Nevertheless,because the model is linear,it can only simulate a unique pattern and cannot simulate EP ENSO or the asymmetries between El Nio and La Nia.

5.　Simulating the two types of ENSO and ENSO asymmetries in GMODEL-ZA

In the last two sections,the EP and CP types of ENSO were simulated separately by the linear air–sea coupled model GMODEL-ZA,confirming the dominant role played by the TH and ZA feedbacks,respectively.In this section,the two types of ENSO are simulated simultaneously in an integrated setup.In addition,the asymmetries between the two phases of ENSO are taken into consideration.

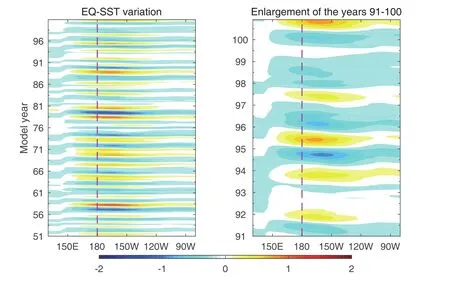
Fig.5.　As in Fig.3 but for the results simulated by the CP ENSO run.

Since GMODEL-ZA is a linear model,the positive and negative phases are totally symmetric,i.e.,the characteristics of El Nio and La Nia are the same.In the observations,however,the cooling center in La Nia is closer to the CP and always has a relatively weak amplitude,compared with that of El Nio.Physically,these two characteristics are tightly correlated,i.e.,when the cooling center is closer to the CP,the SST variation there will be influenced by the relatively weaker TH feedback than that in the EP type of ENSO,and the relatively weaker ZA feedback than that in the CP type of ENSO,which makes the amplitude of La Nia weaker than EP El Nio and stronger than CP El Nio,since the TH feedback is stronger than the ZA feedback.To sum up,during the developing period of ENSO,the sole EP(CP)El Nio will be dominated by strong(relatively weak)TH(ZA)feedback in the EP(CP),while La Nia will be influenced by both weaker-than-EP El Nio TH feedback and weaker-than-CP El Nio ZA feedback.

To simulate the characteristics mentioned above,a simple nonlinear control scheme is added to GMODEL-ZA—namely,letting the model freely integrate at the beginning.When the Nio3 or Nio4 SST index is greater than 0.35°C,the model is sw itched into the El Nio developing scheme.Then,if the Nio3 index is greater than the Nio4 index,the model is sw itched into the EP ENSO scheme,i.e.,the ZA feedback is turned off;and if the Nio3 index is less than the Nio4 index,the model is sw itched into the CP ENSO run scheme,i.e.,the TH feedback is turned off.On the other hand,when the Nio3 and Nio4 SST indices are both less than−0.35°C(since La Nia is difficult to divide into two types),the model is sw itched into the La Nia developing scheme.This scheme includes both the weaker-than-EP El Nio TH feedback(i.e.,multiplying the TH feedback of the EP ENSO scheme by a factor of 0.5)and the weaker-than-CP El Nio ZA feedback(i.e.,multiplying the ZA feedback of the CP ENSO scheme by a factor of 0.5),since the observationally anomalous cooling center during La Nia is located west of the anomalous warming center during EP Nio but east of that during CP Nio.

As the purpose of this experiment is to simulate the diversities in ENSO,Fig.6 shows the leading two CEOF patterns of the anomalous SST,Taux and TCD of the 51st–100th model years simulated in this run,which is termed the NLCTRL run.The following descriptions of the CEOF patterns are all from the perspective of the positive phase.For the first CEOF patterns,the three fields show an EP El Nio pattern and explain 40.31%of the variation,with the warming SST area located in the EP region;accordingly,the TCD deepens in the EP and shallows in the west,confirming the important role played by the TH feedback over the EP.This indicates that the primary SST variations exist in the EP,and the TCD variations exhibit an east–west seesaw pattern.In addition,the strong westerlies are mainly concentrated in the CP and WP,while the weak easterlies are located in the EP and far WP.For the second CEOF patterns(which explains 30.2%of the variation),the SST exhibits a distribution that is more like the CP type of ENSO,but with a slightly eastward shift;accordingly,the TCD deepens in the CP and shallows on both sides.Compared to the CP type of ENSO(Fig.4c),the TCD of this pattern deepens more significantly in the CP.This is because the TH feedback in this region plays a more important role in this experiment for supporting the develop-ment of La Nia,as compared to that in the sole CP ENSO simulation.In addition,Taux showsa pattern that is more like the CP type,with the westerly wind stress anomalies showing a significant westward shift compared with that of the EP ENSO,and the easterlies in the EP have a larger zonal stretch and amplitude.

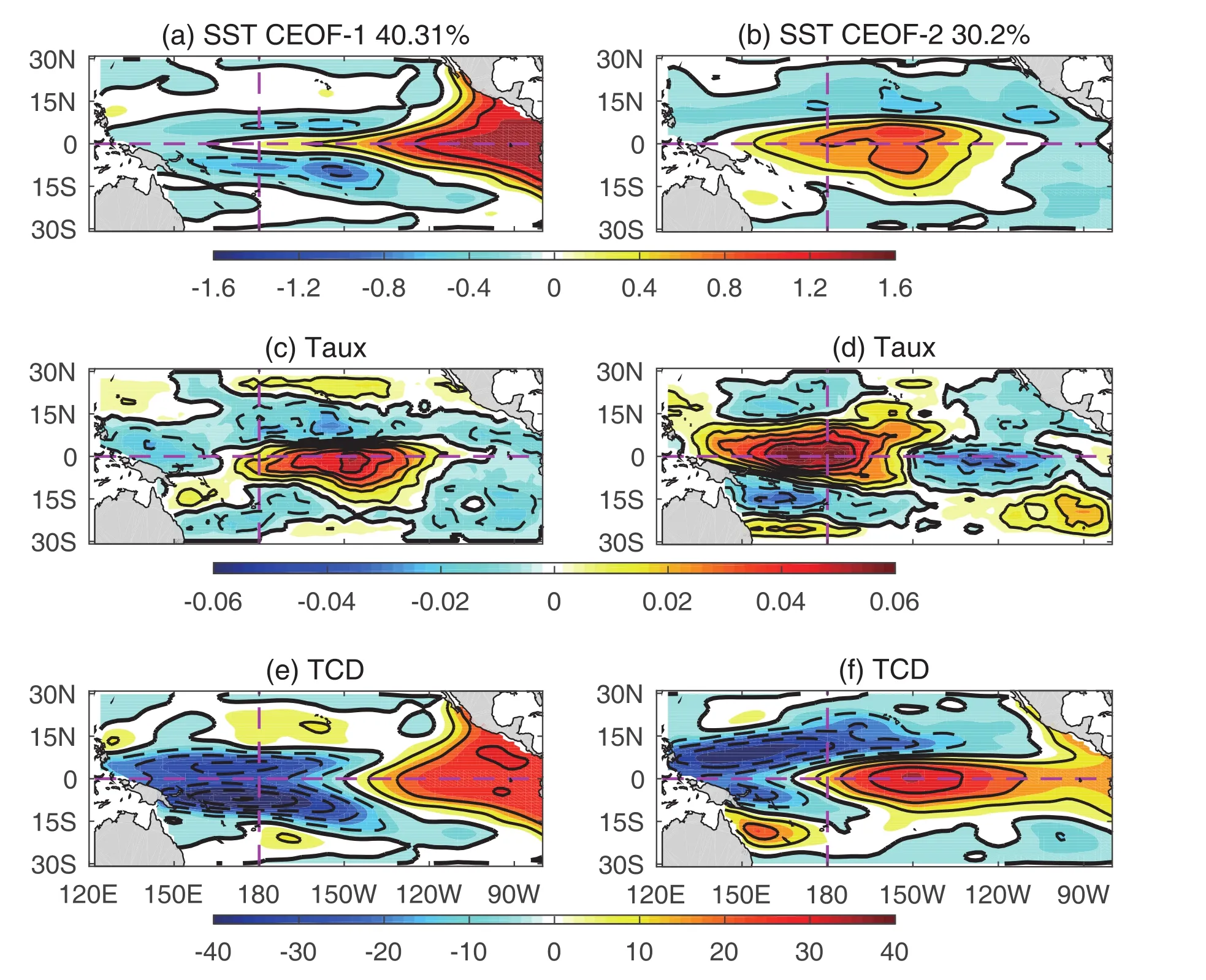
Fig.6.　Leading two CEOF patterns of(a,b)SST,(c,d)Taux and(e,f)TCD of the 51st–100th model years simulated by the NLCTRL run.The numbers at the top of(a)and(b)indicate the percentage of variance explained by the CEOF modes.Contour intervals are 0.4,0.01,and 10 for SST,Taux and TCD,respectively.Purple dashed lines in each panel are along the equator and dateline.

Figure 7 gives the time–longitude diagram for monthly SST anomalies along the equator.As expected,the SST variation patterns capture both the EP and CP El Nio types,with the CP type having a weaker amplitude.Meanwhile,the center and amplitude of some simulated La Nia events are also situated between the CP and EP types of El Nio,which bear a strong resemblance to the observations.The power spectrum of the Nio3.4 SST index shows that the major period of this NLCTRL run is concentrated in 2–5 years,with 4.04 and 2.7 years being the most significant,which is also consistent with the observations.This indicates that,through the simple nonlinear control method,many ENSO characteristics,including the CP and EP type of El Nio and the asymmetries between El Nia and La Nia,can be captured well using the simple linear air–sea coupled GMODEL-ZA.

6.　Summary and discussion

It has been widely mentioned in observational analyses that the TH and ZA feedbacks play a dom inant role in the development of EP and CP ENSO,respectively.In this paper,a simple linear air–sea coupled model,GMODEL,is modified to correctly describe the ZA process,which is linearly related to the zonal current anomalies.This is then substituted for the original so-called wind stress feedback that is linearly related with the zonal wind stress anomalies in the model.The other settings of GMODEL,including the strength distribution of the TH and ZA feedbacks that bear a strong resemblance to the observations,are retained.The modified GMODEL is termed GMODEL-ZA.The results of the CTRL run mainly re fl ect the characteristics of the typical EP type of ENSO.This,on the one hand,demonstrates that the description of the air–sea interaction in the equatorial Pacific is reasonable;while on the other hand,it re fl ects the fact that the general purpose of previous ENSO models is to convincingly simulate the traditional EP type of ENSO,which is also referred to as canonical ENSO.

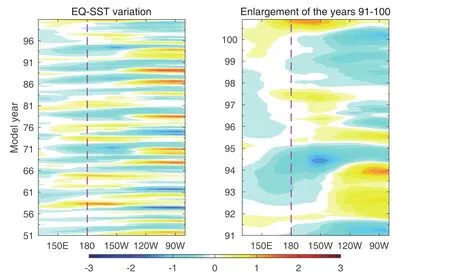
Fig.7.　As in Fig.3 but for the results simulated by the NLCTRL run.

The TH feedback in GMODEL-ZA is switched off to simulate the sole CP type of ENSO.This is done because the TH feedback is much stronger than the ZA feedback in influencing the SST development,which will mean that even though the original warming center occurs in the CP region,the SST in the EP will grow to be higher than that in the CP during the developing period,and the event will eventually develop into an EP type.The results of this CP ENSO run indeed manifest the main characteristics of CP ENSO,both in the anomalous patterns and in the equatorial SST variations.These two experiments con firm the dominant role played by the TH and ZA feedbacks in the development of the EP and CP types of ENSO,respectively.

However,because the model is linear,it can only simulate aunique ENSO pattern on the specific settings,and induce totally symmetric El Nio and La Nia events.To simulate the characteristics of the two types of El Nio and all the ENSO asymmetries,a simple nonlinear control scheme,which gives different settings under these three circumstances,is added to GMODEL-ZA.The result of this NLCTRL run indeed bears a strong resemblance to the observations,i.e.,it effectively exhibits the characteristics of both the EP and CP types of El Nio,and the center and amplitude of some simulated La Nia events are also situated between the CP and EP types of El Nio.This indicates that,through the simple nonlinear control method,many ENSO characteristics can be captured well using the simple linear air–sea coupled GMODEL-ZA,largely due to the realistic description of the two most important processes over the CP to EP regions,i.e.,the TH and ZA feedbacks,in the model.

Analyzing the historical simulation results of CM IP5,Fang et al.(2015)indicated that most state-of-the-art models can accurately simulate the main characteristics of EP ENSO,which was regarded as the only ENSO type before the concept of the CP type emerged.This is also consistent with the verification that the extended-range of ENSO had met with encouraging results during the 1990s when the EP type of ENSO prevailed(Kirtman and Schopf,1998;Latif et al.,1998;Chen et al.,2004).However,severe biases exist in models when capturing realistic CP El Nio structures,i.e.,barely any model can simulate the significantly weaker warming anomalies in the EP(when compared to those in the CP).This is also a reason why the ENSO forecast skill during the recent period of 2002–11,when the CP type of ENSO began to occur more frequently,is relatively low compared to that in the 1980s and 1990s(Wang et al.,2010;Barnston et al.,2012;Xue et al.,2013;Zheng et al.,2016).Many observational analyses have demonstrated that the ZA feedback plays the dom inant role in the development of CP ENSO.The experiments conducted using GMODEL-ZA also confi rm that,using a reasonable depiction of the ZA feedback,the model can produce a reasonable simulation.Looking back at the performance of GCM s,nearly all show a common bias when constructing climatological SST distributions,i.e.,the simulated cold tongue stretches much farther west than observed.This leads to a significant equatorial cold SST bias in the central–eastern Pacific,and pushes the largest mean zonal temperature gradient westward,giving it a narrower zonal stretch than observed.Since the ZA process is the combination of the anomalous zonal current and the mean zonal temperature gradient,this model bias in the mean zonal temperature gradient will give an inaccurate depiction of the ZA feedback,and makes it difficult to simulate a realistic CP ENSO.

Acknowledgements.Theauthorsw ish to thank the two anonymous reviewers for their very helpful comments and suggestions.This work was supported by a project funded by the China Postdoctoral Science Foundation(Grant No.2017M 610225),and the National Natural Science Foundation of China(Grant No.41576019).The author is grateful to Mu MU for his support and comments on the manuscript.The monthly ocean temperature and oceanic circulation data were obtained from http://www.cpc.ncep.noaa.gov/products/GODAS/.

Ashok,K.,S.K.Behera,S.A.Rao,H.Y.Weng,and T.Yamagata,2007:El Nio Modoki and its possible teleconnection.J.Geophys Res.,112,C11007,https://doi.org/10.1029/2006 JC003798.

Barnston,A.G.,M.K.Tippett,M.L.L’Heureux,S.H.Li,and D.G.Dew itt,2012:Skillof real-timeseasonal ENSO model predictions during 2002–11:Is our capability increasing?Bull.Amer.Meteor.Soc.,93,631–651,https://doi.org/10.1175/BAMS-D-11-00111.1.

Behringer,D.,and Y.Xue,2004:Evaluation of the global ocean data assimilation system at NCEP:The Pacific Ocean.Preprints,Eighth Symp.on Integrated Observing and Assimilation Systems for Atmosphere,Oceans,and Land Surface,Seattle,WA,Washington State Convention and Trade Center,Amer.Meteor.Soc.,2.3.[Available online at http://ams.confex.com/ams/pdfpapers/70720.pdf.]

Burgers,G.,and D.B.Stephenson,1999:The“normality”of El Nio.Geophys.Res.Lett.,26,1027–1030,https://doi.org/10.1029/1999GL900161.

Burgers,G.,and G.J.Van Oldenborgh,2003:On the impact of local feedbacks in the central Pacific on the ENSO cycle.J.Climate,16,2396–2407,https://doi.org/10.1175/2766.1.

Burgers,G.,M.A.Balmaseda,F.C.Vossepoel,G.J.Van Oldenborgh,and P.J.Van Leeuwen,2002:Balanced ocean-data assimilation near the equator.J.Phys.Oceanogr.,32,2509–2519,https://doi.org/10.1175/1520-0485-32.9.2509.

Chen,D.K.,M.A.Cane,A.Kaplan,S.E.Zebiak,and D.J.Huang,2004:Predictability of El Nio over the past 148 years.Nature,428,733–736,https://doi.org/10.1038/nature02439.

Fang,X.-H.,and F.Zheng,2014:Effect of decadal changes in air-sea interaction on the climate mean state over the tropical Pacific.Atmos.Oceanic Sci.Lett.,7,400–405,https://doi.org/10.3878/j.issn.1674-2834.14.0019.

Fang,X.-H.,F.Zheng,and J.Zhu,2015:The cloud-radiative effect when simulating strength asymmetry in two types of El Nio events using CM IP5 models.J.Geophys.Res.,120,4357–4369,https://doi.org/10.1002/2014JC010683.

Feng,J.,and J.P.Li,2011:influenc of El Nio Modoki on spring rainfall over south China.J.Geophys.Res.,116,D13102,https://doi.org/10.1029/2010JD015160.

Fu,C.B.,and J.Fletcher,1985:Two patterns of equatorial warming associated with El Nio.Science Bulletin,30,1360–1364.

Ham,Y.G.,J.S.Kug,J.Y.Park,and F.-F.Jin,2013:Sea surface temperature in the north tropical Atlantic as a trigger for El Nio/Southern Oscillation events.Nature Geoscience,6,112–116,https://doi.org/10.1038/ngeo1686.

Jin,F.-F.,1997:An equatorial ocean recharge paradigm for ENSO.Part I:Conceptual model.J.Atmos.Sci.,54,811–829,https://doi.org/10.1175/1520-0469(1997)054<0811:AEORPF>2.0.CO;2.

Jin,F.-F.,S.I.An,A.Timmermann,and J.X.Zhao,2003:Strong El Nio events and nonlinear dynamical heating.Geophys.Res.Lett.,30,1120,https://doi.org/10.1029/2002GL016356.

Kanam itsu,M.,W.Ebisuzaki,J.Woollen,S.-K.Yang,J.J.Hnilo,M.Fiorino,and G.L.Potter,2002:NCEP-DEO AM IP-II Reanalysis(R-2).Bull.Amer.Meteor.Soc.,83,1631–1643,https://doi.org/10.1175/BAMS-83-11-1631.

Kao,H.Y.,and J.-Y.Yu,2009:Contrasting eastern-Pacific and central-Pacific types of ENSO.J.Climate,22,615–632,https://doi.org/10.1175/2008JCLI2309.1.

Kim,H.-M.,P.J.Webster,and J.A.Curry,2009:Impact of shifting patterns of Pacific Ocean warming on North Atlantic tropical cyclones.Science,325,77–80,https://doi.org/10.1126/science.1174062.

Kirtman,B.P.,and P.S.Schopf,1998:Decadal Variability in ENSO Predictability and Prediction.J.Climate,11,2804–2822,https://doi.org/10.1175/1520-0442(1998)011<2804:DVIEPA>2.0.CO;2.

K leeman,R.,1993:On the dependence of hindcast skill on ocean thermodynamics in a coupled ocean-atmosphere model.J.Climate,6,2012–2033,https://doi.org/10.1175/1520-0442(1993)006<2012:OTDOHS>2.0.CO;2.

Kug,J.-S.,F.-F.Jin,and S.-I.An,2009:Two types of El Nio events:Cold tongue El Nio and warm pool El Nio.J.Climate,22,1499–1515,https://doi.org/10.1175/2008JCLI2624.1.

Kumar,K.K.,B.Rajagopalan,M.Hoerling,G.Bates,and M.Cane,2006:Unraveling the mystery of Indian monsoon failure during El Nio.Science,314,115–119,https://doi.org/10.1126/science.1131152.

Larkin,N.K.,and D.E.Harrison,2005:Global seasonal temperature and precipitation anomalies during El Nio autumn and winter.Geophys.Res.Lett.,32,L16705,https://doi.org/10.1029/2005GL022860.

Latif,M.,1987:Tropical ocean circulation experiments.J.Phys.Oceanogr.,17,246–263,https://doi.org/10.1175/1520-0485(1987)017<0246:TOCE>2.0.CO;2.

Latif,M.,and Coauthors,1998:A review of the predictability and prediction of ENSO.J.Geophy.Res.,103,14 375–14 393,https://doi.org/10.1029/97JC03413.

Lee,T.,and M.J.McPhaden,2010:Increasing intensity of El Nio in the central-equatorial Pacific.Geophys.Res.Lett.,37,L14603,https://doi.org/10.1029/2010GL044007.

Philip,S.Y.,and G.J.V.Van Oldenborgh,2010:Atmospheric properties of ENSO:Models versus observations.Climate Dyn.,34,1073–1091,https://doi.org/10.1007/s00382-009-0579-7.

Smith,T.M.,R.W.Reynolds,T.C.Peterson,and J.Law rimore,2008:Improvements to NOAA’s historical merged landocean surface temperature analysis(1880–2006).J.Climate,21,2283–2296,https://doi.org/10.1175/2007JCLI2100.1.

Su,J.Z.,R.H.Zhang,T.Li,X.Y.Rong,J.-S.Kug,and C.-C.Hong,2010:Causes of the El Nio and La Nia amplitude asymmetry in the equatorial eastern Pacific.J.Climate,23,605–617,https://doi.org/10.1175/2009JCLI2894.1.

Sun,D.Z.,and T.Zhang,2006:A regulatory effect of ENSO on the time-mean thermal strati fi cation of the equatorial upper ocean.Geophys.Res.Lett.,33,L07710,https://doi.org/10.1029/2005GL025296.

Vimont,D.J.,D.S.Battisti,and A.C.Hirst,2001:Footprinting:A seasonal connection between the tropics and mid-latitudes.Geophys.Res.Lett.,28,3923–3926,https://doi.org/10.1029/2001GL013435.

Vimont,D.J.,J.M.Wallace,and D.S.Battisti,2003:The seasonal foot printing mechanism in the Pacific:Implications for ENSO.J.Climate,16,2668–2675,https://doi.org/10.1175/1520-0442(2003)016<2668:TSFM IT>2.0.CO;2.

Wang,W.Q.,M.Y.Chen,and A.Kumar,2010:An assessment of the CFS real-time seasonal forecasts.Wea.Forecasting,25,950–969,https://doi.org/10.1175/2010WAF2222345.1.

Xiang,B.Q.,B.Wang,and T.Li,2013:A new paradigm for the predominance of standing Central Pacific warming after the late 1990s.Climate Dyn.,41,327–340,https://doi.org/10.1007/s00382-012-1427-8.

Xue,Y.,M.Y.Chen,A.Kumar,Z.-Z.Hu,and W.Q.Wang,2013:Prediction skill and bias of tropical Pacific sea surface temperatures in the NCEP Climate Forecast System Version 2.J.Climate,26,5358–5378,https://doi.org/10.1175/JCLI-D-12-00600.1.

Yu,J.-Y.,and H.-Y.Kao,2007:Decadal changes of ENSO persistence barrier in SST and ocean heat content in dices:1958–2001.J.Geophys.Res.,112,125–138,https://doi.org/10.1029/2006JD007654.

Yu,J.-Y.,and S.T.Kim,2011:Relationships between extratropical sea level pressure variations and the central Pacific and eastern Pacific types of ENSO.J.Climate,24,708–720.https://doi.org/10.1175/2010JCLI3688.1.

Yu,J.-Y.,H.-Y.Kao,and T.Lee,2010:Subtropics-related interannual sea surface temperature variability in the central equatorial Pacific.J.Climate,23,2869–2884,https://doi.org/10.1175/2010JCLI3171.1.

Zhang,W.J.,F.-F.Jin,J.P.Li,and H.-L.Ren,2011:Contrasting impacts of two-type El Nio over the western north Pacific during boreal autumn.J.Meteor.Soc.of Japan,89,563–569,https://doi.org/10.2151/jmsj.2011-510.

Zhang,W.,Q.-L.Chen,and F.Zheng,2015:Bias corrections of the heat flux damping process to improve thesimulation of ENSO post-2000.SOLA,11,181–185,https://doi.org/10.2151/sola.2015-040.

Zheng,F.,and J.-Y.Yu,2017:Contrasting the skills and biases of deterministic predictions for the two types of El Nio.Adv.Atmos.Sci.,34(12),1395–1403,https://doi.org/10.1007/s00376-017-6324-y.

Zheng,F.,X.-H.Fang,J.-Y.Yu,and J.Zhu,2014:Asymmetry of the Bjerknes positive feedback between the two types of El Nio.Geophys.Res.Lett.,41,7651–7657,https://doi.org/10.1002/2014GL062125.

Zheng,F.,W.Zhang,J.-Y.Yu,and Q.-L.Chen,2015:A possible bias of simulating the post-2000 changing ENSO.Science Bulletin,60(21),1850–1857,https://doi.org/10.1007/s11434-015-0912-y.

Zheng,F.,X.-H.Fang,J.Zhu,J.-Y.Yu,and X.-C.Li,2016:Modulation of Bjerknes feedback on the decadal variations in ENSO predictability.Geophys.Res.Lett.,43,12 560–12 568,https://doi.org/10.1002/2016GL071636.

Zhu,J.,G.Zhou,R.-H.Zhang,and Z.Sun,2011:On the role of oceanic entrainment temperature(Te)in decadal changes of El Nio/Southern Oscillation.Annales Geophysicae,29(3),529–540,https://doi.org/10.5194/angeo-29-529-2011.