铁磁性EE叠氮桥联双核铜配合物磁学性质理论研究

王昌来，罗树常, 2* ，李宏媛，夏维银，张　志

(1.贵州工程应用技术学院 化学工程学院，贵州 毕节　 551700；2.贵州省化学化工实验教学示范中心，贵州 毕节　551700)

叠氮酸根离子具有强的配位能力和丰富的配位模式，采用不同的配位模式与金属离子结合可构筑不同磁学性能的分子基磁体，成为化学、物理学、材料科学等多个领域研究的热点之一[1-8]。由于Cu2+只有一个未成对电子，磁行为较简单，以叠氮酸根离子为桥，Cu2+为自旋载体，合成了大量的叠氮铜系配合物[1-8]。在叠氮桥联双核铜配合物中，叠氮配体的配位模式主要有μ2-1,1 N3和μ2-1,3 N3两种，如图1所示。

图1　叠氮配体主要的配位模式

在这两种配位模式中，μ2-1,1 N3主要传递铁磁性相互作用，μ2-1,3 N3主要传递反铁磁性相互作用[9]。但仍有少数μ2-1,3 N3叠氮铜配合物呈现铁磁性相互作用[1]。本文采用Mukherjee P S教授等[1]以叠氮酸根离子和席夫碱配体合成的铁磁性叠氮铜配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]来研究顺磁中心Cu2+间的磁交换作用机理，通过与变温磁化率拟合的实验值进行对比来检测密度泛函理论结合对称性破损态方法(DFT-BS)计算叠氮铜双核配合物磁耦合常数的准确性及泛函、基组的可靠性，以期为叠氮铜系配合物磁学性质的研究提供一定理论参考。

1　计算方法及模型

1.1　计算模型

图2　配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2〗结构

为考察DFT-BS方法下计算叠氮铜配合物磁耦合常数时泛函、基组等因素对计算结果的影响，选取铁磁性μ2-1,3 N3叠氮桥联配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]为计算模型，如图2所示。计算所用结构均来自X-射线单晶衍射数据，未作改动。

1.2　计算方法

两个顺磁中心间相互作用可用HDVV哈密顿量描述：

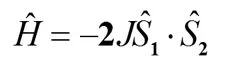
(1)

J表示两个顺磁中心的磁耦合常数，其符号和绝对值的大小表达了顺磁中心间磁耦合作用大小和强弱[10]。J > 0，顺磁中心是铁磁性相互作用，J < 0，则为反铁磁性相互作用[10]。

采用DFT-BS方法计算叠氮铜双核过渡金属配合物的磁耦合常数，计算公式为：

(2)

2　结果与讨论

2.1　磁耦合常数J

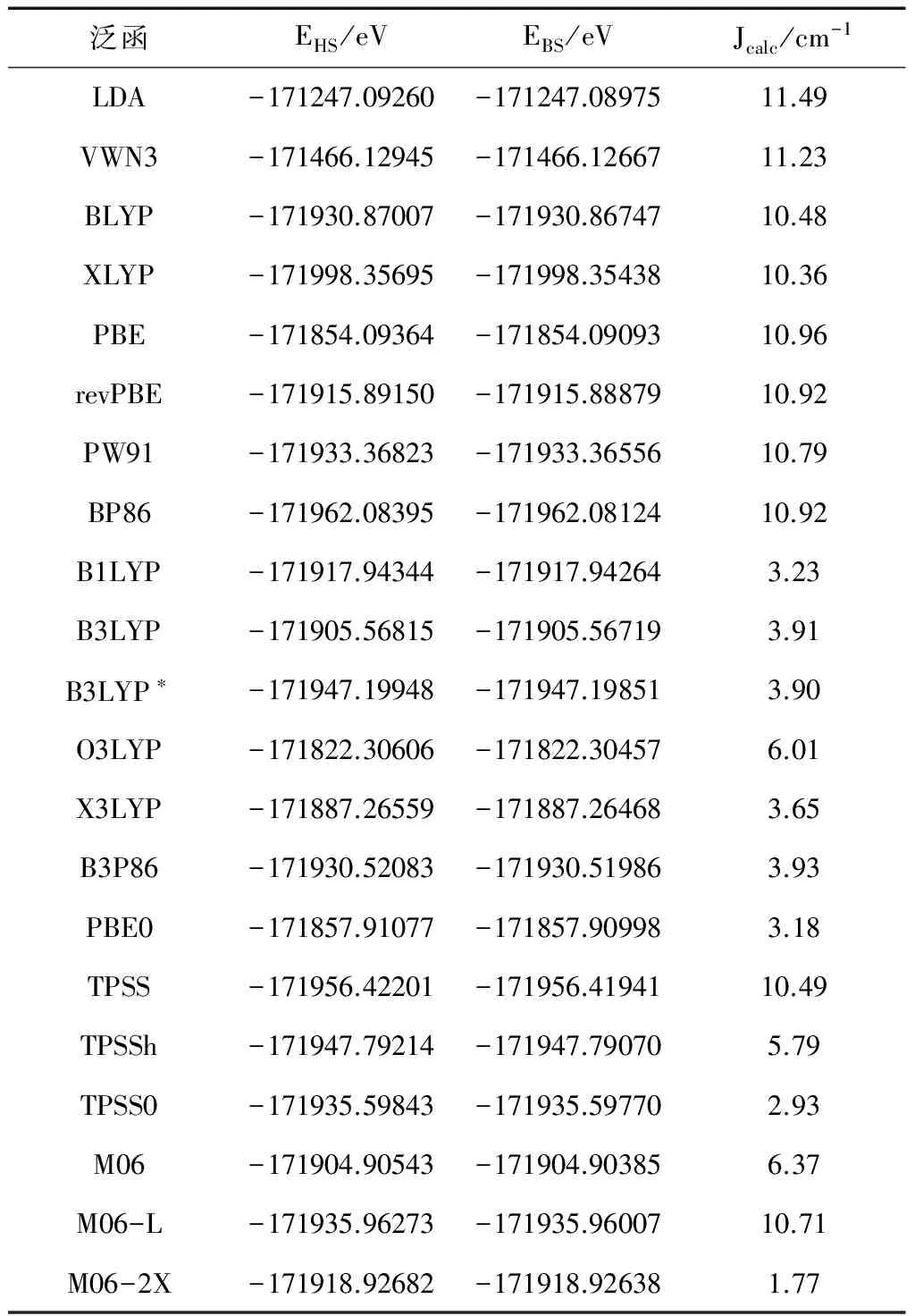
表1　def2-TZVP基组下不同泛函对磁耦合常数J的影响(Jexp = 2.40 cm-1)

采用DFT-BS方法，选取几种密度泛函方法：局域密度近似(LDA、VWN3)、广义梯度近似(GGA)(BLYP、XLYP、PBE、revPBE、PW91和BP86)，杂化密度泛函(HDFT)(B1LYP、B3LYP、 B3LYP*、X3LYP, O3LYP、B3P86和PBE0)和meta-GGA(M06、M06-L、M06-2X、TPSS、TPSS0和TPSSh)，在def2-TZVP基组下计算磁耦合常数J值(Jcacl)，结果如表1所示。

由表1可知，四类密度泛函方法计算的磁耦合常数均大于零，表明顺磁中心Cu(1)和Cu(2)间是铁磁性相互作用的，与实验测量结果一致。局域密度近似方法计算的结果在11.23 cm-1至11.49 cm-1之间，与实验值的差值最大。GGA泛函方法计算的数值在10.79 cm-1至11.49 cm-1之间，与实验值2.40 cm-1的相差较大，混合泛函方法计算的结果在3.18 cm-1至6.01 cm-1之间，比GGA泛函方法计算的数值接近实验值。meta-GGA泛函计算的结果在1.77 cm-1至10.71 cm-1之间，其极差达到了8.94cm-1，但是TPSS0泛函方法计算的磁耦合常数Jcacl值为2.93 cm-1，与实验值2.40 cm-1最吻合，所以计算中选用TPSS0泛函方法计算铁磁性μ2-1,3 N3叠氮桥联配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]的磁耦合常数J值。

为了测试基组对计算结果的影响，选用TPSS0泛函方法，在SVP、TZV、TZVP、def2-SVP、def2-TZVP下的计算磁耦合常数Jcacl值，结果见表2。

表2　TPSS0泛函、不同基组下计算HS、BS态能量(E)及磁耦合常数(Jcacl)

由表2可知，在不同基组下采用TPSS0泛函计算铁磁性μ2-1,3 N3叠氮桥联配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]的磁耦合常数，其数值2.93 cm-1至3.19 cm-1之间，其极差为0.26 cm-1，说明基组对配合物磁耦合常数计算的影响较小，所以选择在TPSS0/def2-TZVP水平下研究配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]的磁相互作用机理是合适的。

2.2　分子磁轨道

分析分子磁轨道的组成，有助于理解配合物顺磁中心间的交换作用[10-11,14-15]。在分子磁学中，BS态的自旋电子定域在某一顺磁中心的轨道称为局域分子轨道，HS态下的单占据分子轨道为分子磁轨道[11,14-15]。

由图3的局域磁轨道可以看出，在铁磁性μ2-1,3 N3叠氮桥联配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]中，自旋电子主要是局域在顺磁中心Cu(1)和Cu(2)，直接与顺磁中心相连的配位原子上也获得了部分自旋电子。由图4可知，顺磁中心Cu(1)和Cu(2)与μ2-1,3-N3桥联配体之间存在较强的轨道相互作用，分子磁轨道主要由顺磁中心Cu(1)、Cu(2)的3dz2轨道、3dxz轨道、桥联配体N3-中N原子的p组成。

图3　配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]局域磁轨道

图4　配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]分子磁轨道

2.3　自旋布居分析

分析铁磁性μ2-1,3 N3叠氮铜配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]的自旋密度分布，有利于理解顺磁中心间相互作用机理[10]。顺磁中心与周围配位原子自旋密度相反时为自旋极化机理，相同时则为自旋离域机理[10-12]。

在TPSS0/def2-TZVP水平下计算得到配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2] HS态和BS态的自旋密度，表3列出了HS态下顺磁中心Cu(1)、Cu(2)与周围配位原子的自旋密度，其中正号和黑色为α自旋，负号和灰色为β自旋。

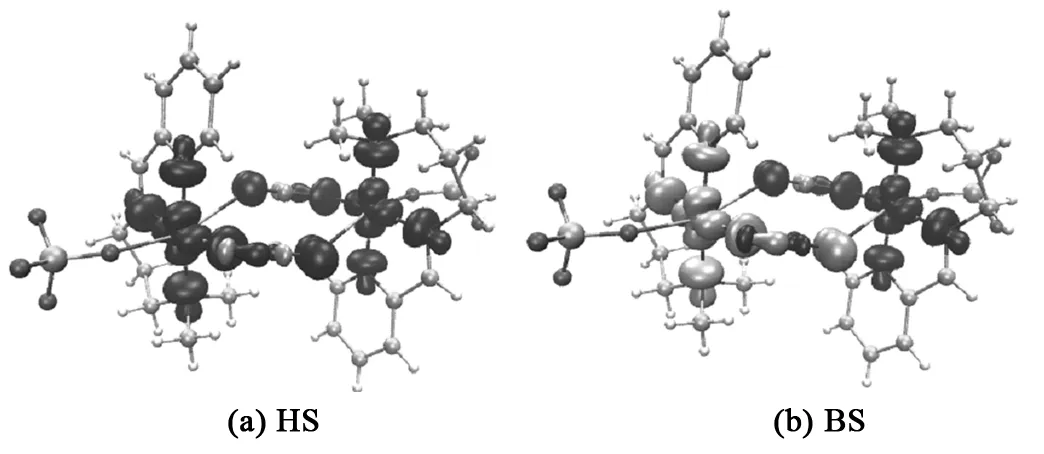
图5　配合物HS和BS态的自旋密度图

由图5可知，无论HS态还是BS态，顺磁中心Cu(1)、Cu(2)、N3-的N原子、席夫碱配体的N原子间的自旋密度符号均相同，说明在配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]中顺磁中心Cu2+间主要是自旋离域作用。由表3可知，在HS态下，顺磁中心Cu(1)和Cu(2)的自旋电子分别为0.626107 e和0.626124 e，明显地离域到周围配体上，使得与之配位的原子获得了部分电子占据，包括桥联配体N(3)、N(4)、N(5)( 0.038554e, -0.018409e, 0.102480e)；N(6)、N(7)、N(8)( 0.038581e, -0.0184079e, 0.102452e)；端基配体N(9)、N(10)、N(11) (0.072191e, 0.079672e, 0.101363e)；N(12)、N(13)、N(14) (0.070817e,0.043009e,-0.040792e)；两个ClO4-离子的氧原子O(15)、O(16)( 0.000559e,0.000559e)。顺磁中心Cu(1)和Cu(2)通过μ2-1,3 N3{N(3)、N(4)、N(5)和N(6)、N(7)、N(8)}以一正一负的方式传递，存在自旋极化作用，μ2-1,3 N3叠氮桥的N原子受到顺磁中心自旋离域和自旋极化的共同作用，以自旋离域为主。

表3　配合物HS态部分原子自旋密度

表3(续)

3　结论

采用DFT-BS方法研究了铁磁性μ2-1,3 N3叠氮桥联配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]，选择局域密度近似、GGA、混合泛函、meta-GGA四类方法计算了配合物的磁耦合常数，选用5种基组(SVP、TZV、TZVP、def2-SVP、def2-TZVP)进行测试。结果表明，四类方法计算的磁耦合常数Jcalc都与实验值符号相同，混合泛函计算的结果都比较接近实验值，但meta-GGA中的TPSS0泛函的计算值与实验值更吻合，基组对磁耦合常数的影响不大。所以，选择在TPSS0/def2-TZVP水平下研究铁磁性μ2-1,3 N3叠氮桥联配合物[Cu2(L2)2(μ2-1,3-N3)2(ClO4)2]的磁学性质。自旋布居分析显示，顺磁中心Cu(1)、Cu(2)间相互作用以自旋离域为主。分子磁轨道分析表明，顺磁中心Cu(1)和Cu(2)与μ2-1,3-N3桥联配体之间存在较强的轨道相互作用，分子磁轨道主要由顺磁中心Cu(1)、Cu(2)的 轨道3dz2、3dxz轨道、桥联配体N3-中N原子的p组成。

[1]Mukherjee P S,Dalai S,Mostafa G,et al.Synthesis,crystal structure,and magnetic properties of two new Cu(II) complexes with end-to-end azido bridging ligands[J].New J Chem,2001,25(9):1203-1207.

[2]Siddiqi K S.Synthesis,crystal structure,and magnetic properties of single end-to-end azido-bridged 1-D chain coordination polymers of Cu(II)[J].J Coord Chem,2012,65(15):2593-2611.

[3]Adhikary C,Koner S. Structural and magnetic studies on copper(II) azido complexes[J].Coord Chem Rev,2010,254(23-24):2933-2958.

[4]Zhao J P,Xie Y,Li J R,et al.Structural and magnetic modulations of copper(II) azido complexes: unexpected in situ reactions of mono-N-donor pyridine-based co-ligands[J].Dalton Trans,2015,45(4):1514-1524.

[5]Liu X Y,Cen P P,Li F F,et al.A unusual two-dimensional azido-Cu(II) network with benzoate derivative as a co-ligand exhibiting ferromagnetic order and slow magnetic relaxation[J].Rsc Advances,2016,6(98):96103-96108.

[6]Liu X Y,Chen S P,Grancha T,et al. A triple-bridged azido-Cu(II) chain compound fine-tuned by mixed carboxylate/ethanol linkers displays slow-relaxation and ferromagnetic order: synthesis,crystal structure,magnetic properties and DFT calculations[J].Dalton Trans,2014,43(41):15359-15366.

[7]Chakraborty A,Srinivasa R L,Manna A K,et al.Discrete dinuclear complex to extended 2D compound in a Cu-azido system by controlling coligand stoichiometry: synthesis and magneto-structural correlations[J]. Dalton Trans,2013,42(30):10707-10714.

[8]Zhao J P,Xie Y B,Li J R,et al.Structural and magnetic modulations of copper(II) azido complexes: unexpected in situ reactions of mono-N-donor pyridine-based co-ligands[J].Dalton Trans,2016,45(4):1514-1524.

[9]刘翔宇.溶剂诱导的取代基苯甲酸-叠氮铜配合物分子磁体的合成、结构及性能[D].西安: 西北大学,2015.

[10]Neese F.The ORCA program system[J]. WIREs Comput Mol Sci,2012,2(1):73-78.

[11]罗树常,刘翔宇,张竹霞,等.氧桥联稀土钆双核配合物磁学性质的密度泛函理论研究[J]. 分子科学学报,2017,33(2): 120-126.

[12]曹景阳,孙小媛,罗树常,等.氧桥联席夫碱GdCo双核配合物磁学性质理论研究[J].广东化工,2017,44(7):130-132.

[13]Humphrey W,Dalke A,Schulten K.VMD: Visual Molecular Dynamics[J].J Mol Graphics,1996,14(1):33-38.

[14]胡宗超,卫海燕,王凡,等.密度泛函理论在分子磁学中的应用2.混合桥联三核镍配合物自旋交换作用[J].化学学报,2004,62(20):1973-1980.

[15]Bian J Y,Chang Y F,Zhang J P.Theoretical studies on the magnetic bistability of dinickel complex tuned by azide[J].J Phys Chem A,2008,112:3186-3191.