基于特性方程式下的通用AF40-6自动变速器档位分析
2018-04-04屈亚锋
屈亚锋
(武汉交通职业学院 湖北 武汉:430065)
通用AF40-6是一款全自动、六档、电子控制的紧凑型变速驱动桥,适用于前轮驱动和全轮驱动的车辆,在新君越、新君威2.0T等车型上有所应用。[1]该款变速器是典型的多排串联复合式行星齿轮自动变速器,结构复杂、档位多;它充分利用单、双行星齿轮机构“两入一出”动力传递变化获得档位,使档位分析变得更复杂,学生理解困难;同类文献对该款变速器研究较少,文献[1]或维修手册中直接告知各档位的执行元件,并未说明选用方法和传动比的计算过程。本文通过理解通用AF40-6自动变速器变速传动机构的结构,以单排单、双行星齿轮机构不同运动方式的应用情况为基础,对各档位换档执行元件的选择方法进行分析,从而得出各档位最优化的换档执行元件,使学生容易掌握和理解。
1 单排单、双行星齿轮机构简介
1.1 单排单、双行星齿轮机构的特性方程式
通用AF40-6自动变速器齿轮变速传动机构中采用了拉维娜式结构,拉维娜式结构是由单排单、双行星齿轮机构组合而成的双排复合式结构,结构简化如图1所示,其共用齿圈和行星架。假设大太阳轮转速n1,齿圈的转速n2,行星架的转速n3,小太阳轮转速n4,齿圈与大太阳轮齿数比为α1,齿圈与小太阳轮齿数比为α2。则单排单、双行星齿轮变速机构运动规律的特性方程式为:
n1+α1n2-(1+α1)n3=0
(1)
n4-α2n2-(1-α2)n3=0
(2)
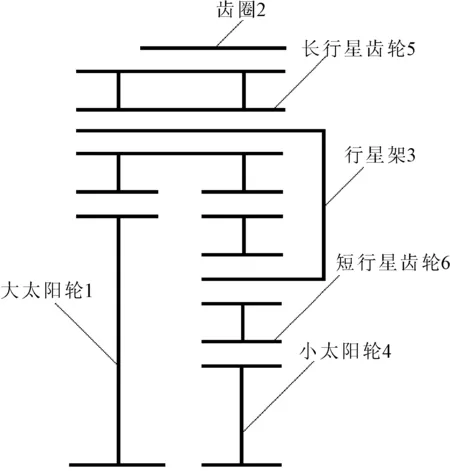
图1 拉维娜式行星齿轮机构的结构图
1.2 单排单、双行星齿轮机构的运动方式和应用情况
根据式(1)和式(2)不同的动力传递,可实现单排单行星齿轮机构的不同运动方式,具体见表1[2]。表1与传统归纳的不同点主要有:一是并未将单排行星齿轮机构的所有运动方式都列举出来,仅保留了目前应用于自动变速器的运动方式;二是增加了方案6和方案10,即“两入一出”且两入速度不等的运动方式;三是给出了每种运动方式的传动比变化范围,归纳了其可能应用的档位和档位特点;四是方案3传动比大小加了绝对值符号,“-”表示输入输出反向。

表1 单排行星齿轮齿轮机构不同运动方式及应用

图2 通用AF40-6自动变速器的变速传动机构
2 通用AF40-6自动变速器的变速传动机构
通用AF40-6自动变速器变速传动机构的结构如图2所示,属于典型的串联复合式行星齿轮机构,从动力输入端来看,分别假定为第1、2和3排,第1排为单行星齿轮机构,第2、3排是拉维娜式组合行星齿轮机构,各排的参数分别假定为α1、α2和α3[3]。该变速传动机构结构有如下几大特点:一是第1排太阳轮与液力变矩器单向离合器内座圈相连接,被其固定不能旋转;二是动力由输入轴1输入,然后经过两条路线传递,一条是直接经过离合器C2传递至第2、3排共用行星架,另外一条经过第1排行星齿轮组减速后通过C1或C3传递至第3排太阳轮或第2排前太阳轮;三是第2、3排共用齿圈且做为动力输出;四是可实现六个前进档位,但无直接档。
3 通用AF40-6自动变速器各档位分析
3.1 “D”档位分布情况分析
通用AF40-6自动变速器中数字6表示“D”档位数为6个(D1、D2、D3、D4、D5、D6)。
根据图2,第1排只能实现表1方案2,可获得(1+α1)/α1大小的传动比;由于第1排无法实现直接档,而第1排和第2、3排是串联关系,故该款变速箱无法实现直接档。由于第2、3排属于拉维娜式结构,不考虑C1、C2和C3传递动力的转速差时,比较容易获得表1方案8、方案5或方案9和方案4,即:α3、1和α2/(1+α2)大小的传动比;如果第2、3排同时起作用,即C1、B1起作用时,可获得(α2+α3)/(1+α2)大小的传动比[4]。根据串联复合式变速器获得传动比的方法,第1排和第2、3排分别匹配,能够实现1个超速档和3个低速档。
考虑到C2和C1、C3传递动力时有转速差,可实现表1方案6和方案10;由于C1C2或C2C3分别在单行星齿轮排和双行星齿轮排,故不能同时实现两个超速档或两个低速档,即只能获得1个超速档和1个低速档。
因此,通用AF40-6自动变速器“D”档位分布情况为:2个超速档(D5和D6),4个低速档(D1、D2、D3和D4)。
3.2 通用AF40-6自动变速器各档位分析方法
3.2.1“D”档位分析
3.2.1.1D1档位分析
(1)D1档位与执行元件的关系
由于D1档位是D位的最低档,即最大的传动比,因此第1排与第2、3排匹配时应选择最大的传动比,故选用C1、B2或C1、F1;由于D1档位不是D位的最高档,设计时如果有制动或单向制动两种约束条件时,一般选择单向约束条件,使D1档位无发动机的制动作用,故选用F1,主要作用是阻止第3排行星架逆时针转动[5]。因此,D1档的最优换档执行元件为:C1、F1。
(2)D1档位传动比的计算
n11+α1n12-(1+α1)n13=0(第1排)(3)
n11=0
(第1排)(4)
n31-α3n32-(1-α3)n33=0(第3排)(5)
(第3排)(6)
由式(3)、(4)、(5)、(6)联立求解D1档传动比:
iD1=(n12/n13)×(n31/n32)=(1+α1)/α1×α3
3.2.1.2D2档位分析
(1)D2档位与执行元件的关系
由于D2档位也是低速档,但比D1档位的传动比小,故考虑C1、B1起作用时,通过(α2+α3)/(1+α2)大小的传动比与第1排匹配,可获得比D1档位稍小的传动比;比较D1档和D2档的选择方案,仅差1个由液压控制控制的B1元件。因此,D2档的最优换档执行元件为:C1、B1。
(2)D2档位传动比的计算
n21+α2n22-(1+α2)n23=0(第2排)(7)
n22=0
随着科学技术的突飞猛进、社会经济的迅速发展以及文化交流的日趋频繁,大量的新词涌入英汉语言。目前关于英汉词汇构词法的研究很多,但对英汉新词构成模式之间的比较研究却相对较少。本文通过对比英汉新词的构词方法,找出英汉新词构成的相似性和独特性,并且进一步分析造成英汉构词差异的原因,帮助外语学习者了解英汉新词的构词规律、语义特点及其社会文化内涵,加深对英汉语言的认识。
(第2排)(8)
n23=n33;n22=n32
(第2、3排)(9)
由式(3)、(4)、(5)、(7)、(8)、(9)联立求解D2档传动比:
iD2=(n12/n13)×(n31/n32或n22)=
(1+α1)/α1×(α2+α3)/(1+α2)
3.3.1.3D3档位分析
①D3档位与执行元件的关系
由于D3档也是低速档,但比D2档位的传动比小,根据前文对D1和D2档位的分析,继续考虑第1和第2、3排匹配的方法,第2、3排能够选择的比1大的传动比已经选择,故只能选择表1方案5或方案9;由于C2和C1、C3传递动力时有转速差,只能选择C1、C3;比较D2档和D3档的选择方案,虽然相差的由液压控制的元件有B1、C3,但是B1、C3必须选择,故已经是最优方案。因此,D3档的最优换档执行元件为:C1、C3。
(2)D3档位传动比的计算
n21=n31
(第2、3排)(10)
由式(3)、(4)、(5)、(7)、(9)、(10)联立求解D4档传动比:
iD3=(n12/n13)×(n31或n21/n32或n22)=
(1+α1)/α1×1
3.2.1.4D4档位分析
(1)D4档位与执行元件的关系
由于D4档也是低速档,但比D3档位的传动比小,根据前文对D1、D2和D3档位的分析,第1和第2、3排匹配方案已经全部选用,故考虑表1方案6或方案10,即选择C1、C2或C2、C3;由于C2单独起作用用于第2排可实现超速档,而用于第3排只能实现低速档,故选择C1、C2;比较D3档和D4档的选择方案,虽然相差的由液压控制的元件有C2、C3,但是C2、C3必须选择,故已经是最优方案。因此D4档的最优换档执行元件为:C1、C2。
(2)D4档位传动比的计算
(1+α1)/α1×n31=n33(第3排)(11)
由式(5)、(11)联立求解D4档传动比:
iD4=n33/n32=(α1×α3+α3)/(α1×α3+α3-1)
3.2.1.5D5档位分析
(1)D5档位与执行元件的关系
由于D5档位是超速档,但传动比比D6档稍大,根据前文D4档的选择方案分析,只能选择C2、C3;比较D4档和D5档的选择方案,虽然相差的由液压控制的元件有C1、C3,但是C1、C3必须选择,故已经是最优方案。因此D5档的最优换档执行元件为:C2、C3。
(2)D5档位传动比的计算
(1+α1)/α1×n21=n23(第2排)(12)
由式(7)、(12)联立求解D5档传动比:
iD5=n23/n22=(α1×α2+α2)/(α1×α2+α2+1)
3.2.1.6D6档位分析
(1)D6档位与执行元件的关系
由于D6档位是该变速箱的最高档位,可考虑表1方案4,故选择C2、B1;比较D5档和D6档的选择方案,虽然相差的由液压控制的元件有B1、C3,但是B1、C3必须选择,故已经是最优方案。因此D6档的最优换档执行元件为:C2、B1。
(2)D6档位传动比的计算
(1+α1)/α1×n21=n23(第2排)(13)
由式(7)、(13)联立求解D6档传动比:
iD6=n23/n22=(α1×α2+α2)/(α1×α2+α2+1)
3.2.2“R”档位分析
(1)R档位与执行元件的关系
根据表1,方案3可实现倒档;根据图2只有第2排可实现;根据前述D1档位执行元件的选择,考虑到倒档可采用发动机的制动作用,故R档的最优换档执行元件为:C3、B2。
(2)R档位传动比的计算
n23=0
(第2排)(14)
由式(3)、(4)、(7)、(14)联立求解R档传动比:
iR=(n12/n13)×(n21/n22)=(1+α1)/α1×-α2
(“-”号表示输入输出反向)
3.2.3手动“1”档位分析
手动“1”档是通用AF40-6自动变速器的手动换档模式下的档位,它与D1档的区别是可利用发动机的制动作用。因此手动“1”档位的换档执行元件为:C1、B2。传动比的计算和D1档位相同。
值得注意的是:由于D2、D3、D4、D5和D6各档位都有发动机制动作用,因此手动换档模式下的其他档位与对应的D档位换档执行元件相同。
3.3 通用AF40-6自动变速器各档位与执行元件的关系
根据前文各档位换档执行元件的分析和传动比计算,通用AF40-6自动变速器各档位与执行元件的关系归纳为表2所示,传动比大小数值来自文献[1]中变速箱的规格数据。表2中通过不同的符号表示各执行元件的工作状态,具体含义为:“●”表示液压元件起作用;“-”表示液压元件不起作用;“H”表示单向离合器起作用;“”表示单向离合器不起作用;“Δ”表示空档时起作用的液压元件。

表2 通用AF40-6自动变速器各档位与执行元件的关系
4 结论
本文分析通用AF40-6自动变速器时,并未直接采用文献[1]中各档位的换档执行元件,而是在事先不知道各档位换档执行元件的情况下,利用单、双行星行星齿轮机构特性方程式,结合不同运动方式的应用情况,特别是充分利用任意两个共同输入且速度相等或不相等动力传递的变化,通过分析各档位传动比大小的范围,研究出通用AF40-6自动变速器各档位最优化换档执行元件选择的方法,最后计算出传动比,和文献[1]中各档位传动比大小的范围基本吻合。文中理论分析准确、严谨,讲清了如何选择换档执行元件,对其他研究自动变速器的学者有一定的参考价值。
[1]上海通用AF40-6自动变速箱技术信息指南[EB/OL].(2015-02-01)[2017-11-28].http://www.doc88.com/p-0592619127820.html.
[2]屈亚锋.基于特性方程式下的自动变速器档位分析技巧[J].武汉船舶职业技术学院学报,2017,(3):39-42.
[3]屈亚锋.基于瞬心-速度矢量法分析单排行星齿轮机构中“两入一出”动力传递的变化[J].信息记录材料,2017,(12):59-62.
[4]刘刚,屈亚锋.汽车底盘电控系统检修[M].北京:中国铁道出版社,2017:54-56.
[5]屈亚锋.自动变速器档位中发动机制动作用的判断技巧——以丰田A340E为例[J].淮北职业技术学院学报,2017,(6):137-139.
