无取向电工钢棘轮变形的实验研究

杜丽影　刘　冬　尚　伦　邝兰翔

(宝钢股份中央研究院武汉分院(武钢有限技术中心)　湖北　武汉：430080)

金属材料在循环加载条件下将产生不可逆变形的循环累积现象，即为棘轮效应。这是材料循环塑性中一个基本现象，在结构件的安全设计和评定中必须加以考虑。材料的棘轮行为已引起学者的广泛重视，并进行了大量的试验和理论研究[1-4]。

随着电动汽车的快速发展，电动汽车电机转子用无取向电工钢的疲劳行为已引起关注，一方面，较大的变形量减小了电机转子和定子之间的间隙，增加了转子和定子接触的概率，从而导致电机报废；另一方面，这种不可恢复变形一旦使电工钢破裂，产生的碎片将阻止转子旋转，严重损伤电机功能，降低电机使用寿命。因此，电动汽车电机设计时必需考虑转子的棘轮变形量。这直接决定电机的使用性能及安全寿命。然而，目前对于无取向电工钢的研究主要集中于电磁性能，对其棘轮特性的研究还处于空白阶段。因此，本文将以30WGP1600无取向电工钢为研究对象，分析了电工钢棘轮行为的主要影响因素和棘轮饱和特性，其研究结果能为电动汽车电机的合理设计提供数据支撑。

1　棘轮应变定义

为了反映材料棘轮塑性累积大小，定义单轴棘轮应变为

(1)

国际上关于上式中εR和εL的定义有三种[5]：

εR和εL分别为一个应力-应变循环中的最大和最小塑性应变量，其表达式为：

(2)

εR和εL分别为一个循环中峰值和谷值对应的总应变量，其表达式为：

(3)

εR和εL均为一个循环中峰值对应的总应变量，其表达式为：

(4)

上述各式中的T表示材料的真应力或真应变，则真应力和真应变的表达式分别为：

σT=σ(1+ε)

(5)

εT=ln(1+ε)

(6)

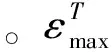
2　实验

2.1　实验材料

实验用材料为工业化生产冷轧无取向电工钢，牌号为30WGP1600，厚度0.3mm，主要化学成分见表1所示，常规力学性能见表2。材料的显微组织为铁素体(见图1)，晶粒尺寸大小不均匀，最小尺寸为18μm，最大尺寸可达到230μm，平均晶粒尺寸约为105μm。

表1　实验用钢60WGP1600的化学成分(质量分数/%)

表2　30WGP1600电工钢的力学性能

图1　30WGP1600无取向电工钢的显微组织

2.2　试样制备与试验过程

采用线切割的加工方式，轴向平行于轧制方向，试样加工尺寸如图2所示。平行部长度为30mm，宽度为15mm。试样两侧表面用180#～1800#粒度的砂纸逐级抛光，平行段与过渡弧的转角处用1800#砂纸轻轻抛光，避免试样表面缺陷对测试结果的影响。试样上下表面用酒精清洗干净，防止表面涂层破坏及生锈。

图2　试样加工图

实验在岛津5kN电磁力疲劳实验机上完成，控制模式为轴向载荷控制，加载波形为正弦波，加载频率f为50Hz。采用型号为DH3817F的动静态应变测试分析系统，通过贴应变片的方法采集应变量。该采集系统自带8个采集通道，采集频率小于等于200Hz，采集最大应变值可达到20000με。应变片的型号为BE120-2BA，灵敏系数为2.22，采用双桥式连接方法，实验测试过程见示意图3。独立加载工况见表3和表4。表中σp指单一循环中的峰值应力，R为加载比。表3表示加载比为0.1，加载频率50Hz，测试不同峰值应力(280MPa～400MPa)下棘轮变形量；表4为固定峰值应力为360MPa，分析不同加载比(0.1、0.25)对棘轮变形量的影响。

图3　电工钢棘轮应变测试示意图

加载频率加载比峰值应力σp(MPa)50HzR=0．1280300320340360400

表4　不同加载比的加载工况

3　实验结果与分析

3.1　棘轮变形演化规律

根据上述实验方法，得出30WGP1600无取向电工钢不同加载工况下的棘轮应变与循环周次的关系(见图4)。图4a给出了峰值应力相同，不同加载比下的棘轮变形；图4b给出了加载比为0.1工况下棘轮变形随峰值应力的演变规律。从图4中得出，当峰值应力相同，加载比不同时，棘轮应变随峰值应力的变化规律都相同，可见峰值应力是影响无取向电工钢棘轮变形的主导因素。另外，从图4b中还可以看出，当峰值应力小于300MPa时，材料的棘轮应变为弹性应变，去除外力后，变形可恢复。峰值应力在300MPa～340MPa时，材料有微小的棘轮变形，且在数百周内就达到饱和状态。当峰值应力大于340MPa时，棘轮应变量开始大幅增加，且随着循环周次的增加不断增大，但增大的速率逐渐减小，循环到十万次左右达到饱和状态。

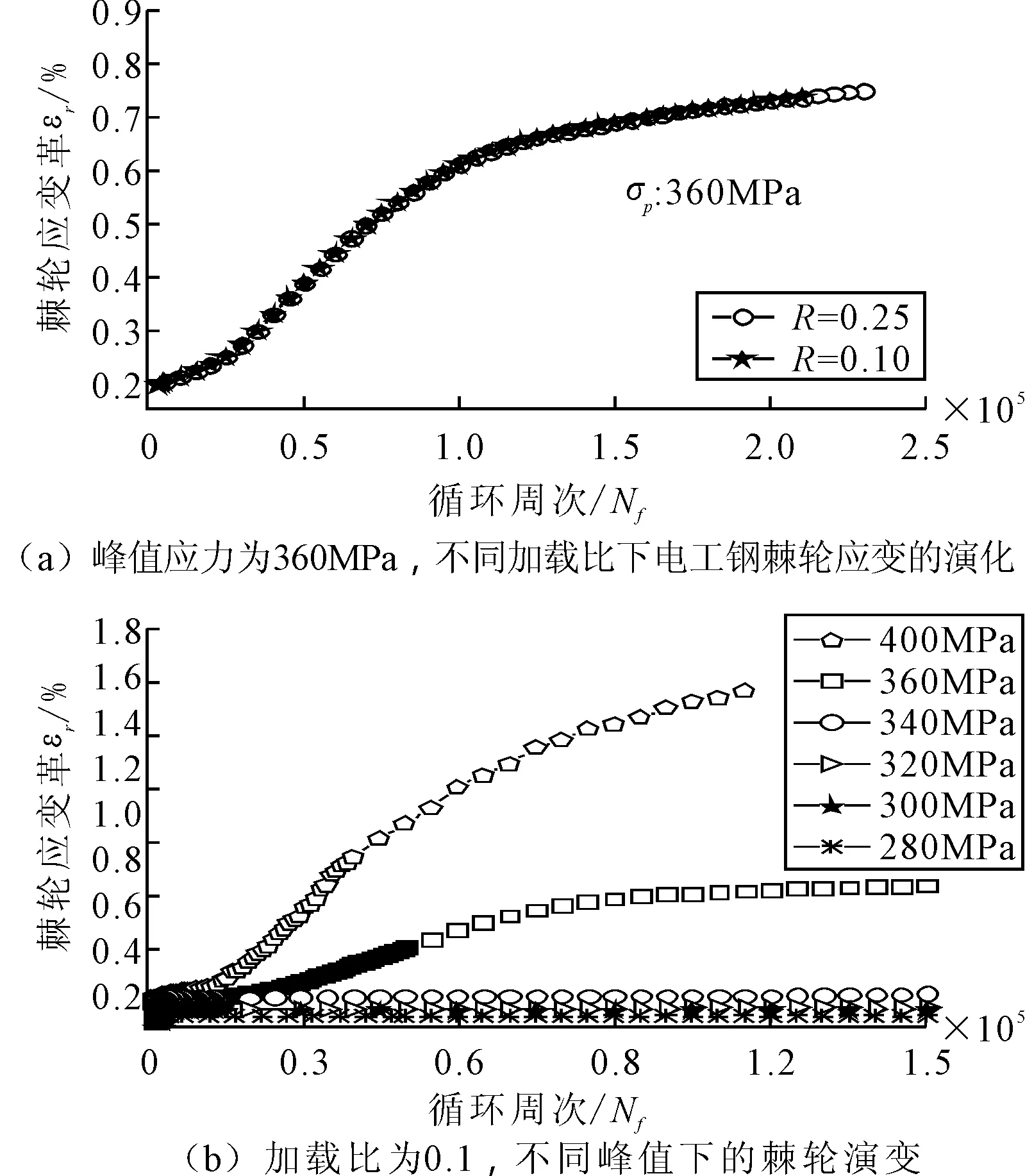
图4　不同独立加载工况下棘轮应变εr 与循环周次Nf的关系

3.2　棘轮饱和特性

当峰值应力小于等于340MPa时，材料循环到1万次均已达到饱和，因此取1万次对应的棘轮变形量为饱和值。当峰值应力大于340MPa时，材料循环到11万次均已达到饱和，因此取该循环次数对应的变形量为饱和值，结果如图5所示。结果表明，峰值应力越大，饱和棘轮变形越大。当峰值应力小于等于340MPa时，饱和棘轮应变随峰值应力的增幅很小，从0.16%增加到0.21%左右；当外加峰值应力大于340MPa小于屈服强度时，饱和棘轮应变量迅速增加，从0.21%增加到1.45%。但在相同峰值应力下，平均应力和应力幅值对饱和棘轮变形量几乎没有影响。这说明，饱和棘轮应变仅受峰值应力一元控制，受平均应力和幅值应力的影响微小。

图5　饱和棘轮应变与峰值应力σp的关系

材料的棘轮变形本质上与位错的运动及增殖过程有关。当外加峰值应力较小时，位错密度较低，可观察到位错的晶粒数目较少。在反向卸载过程中，位错运动比较容易，变形的可恢复性好，不会促进棘轮变形大幅增加，因此，此阶段内(300MPa～340MPa)材料的饱和棘轮变形量增幅微小。当外加峰值应力较大(大于340MPa)时，位错密度增加，多个滑移系启动，大量位错发生缠结和交割，且发生位错缠结的晶粒数目增多，在反向卸载时，位错运动的阻力增加，变形的可恢复性较差，这有助于棘轮变形的累加，饱和棘轮变形量相应迅速增加。

4　结论

本文系统研究了30WGP1600无取向电工钢的棘轮变形规律和棘轮饱和特征值，得出以下主要结论：

(1)在单轴循环应力加载条件下，峰值应力是制约无取向电工钢棘轮变形和饱和棘轮应变的主导因素。

(2)当外加峰值应力小于300MPa时，几乎不发生棘轮变形，30WGP1600无取向电工钢处于弹性变形阶段。当峰值应力大于300MPa小于340MPa，棘轮变形量较小，且循环初期就达到棘轮饱和状态，饱和棘轮应变从0.16%增加到0.21%左右。当峰值应力大于340MPa小于等于屈服强度时，循环十万次左右方能达到稳定。饱和棘轮应变量迅速增加，从0.21%增加到1.45%左右。

[1]Peng Zhao, Fu-Zhen Xuan. Ratchetting behavior of advanced 9-12% chromium ferrite steel under creep-fatigue loadings[J]. Mechanics of Materials,2011,43:299-312.

[2]Feaugas X, Gaudin C. Ratchetting process in the stainless steel AISI 316L at 300K: an experimental investigation[J]. International Journal of Plasticity,2004,20:643-662.

[3]徐尹杰,蔡力勋,刘宇杰.应力作用下316L不锈钢塑性变形行为研究[J].航空学报,2007,28(3):567-573.

[4]蔡力勋,刘宇杰,邱绍宇.T225NG合金的高温单轴棘轮行为研究[J].西安交通大学学报,2004,38(7):762-766.

[5]蔡力勋,牛清勇,刘宇杰.描述不锈钢材料单轴棘轮行为的一元参量体系[J].金属学报,2002,38(9):966-973.