广东坭洲头航道改线工程通航风险研究

王梦紫　高　曦　贾明明

(1.武汉交通职业学院　湖北　武汉:430065；2.泰州海事局　江苏　泰州：225300)

航道的通航安全是船舶安全航行和沿岸港口可持续发展的重要保障。在广州港港口迅速发展的背景下，贸易量持续增加，进出港航道内的船舶数量激增，同时船舶的尺度也在逐年增大，这些因素在一定程度上使得广州港出海航道内的通航风险不断增加。为了保障通航安全以及港口的可持续发展，航道管理部门决定对坭洲头航道进行改线整治。航道改线是一个复杂的工程，涉及到许多方面，改线后航道通航是否安全直接影响着船舶的安全航行和沿岸港口的可持续发展。坭洲头航道改线工程由于地理位置的原因，其通航安全受到多种因素的影响。

广东坭洲头航道改线工程通航风险研究的实际应用意义在于找出影响航道安全的一些不利因素，提前采取相应缓解措施，减少航道内水上交通事故的发生，保障水上安全形势可控，使航道通航更安全的目标得以落实具有重要的意义。

1　坭洲头航道改线工程概况

1.1　航道基本情况

广东坭洲头航道改线工程位于广州港出海航道狮子洋段，改线后航道长度约为8.4千米，由MV1段、V1U1段、U1M′段三部分组成。航道上端与莲花山航道相连，下端与大虎航道相连，同时航道东岸附近有东莞水道，西岸附近有浮莲岗水道。此外，在航道东岸设置有西大坦、立沙岛两作业区。改线后航道边线紧靠港口规划泊位的回旋水域和78NZ锚地的外边线，两端衔接至原航道。此外，航道在V1、U1处的转向点角度分别为20°、27°，采用切角法进行加宽处理。广东坭洲头航道改线工程具体平面布置如图1所示。

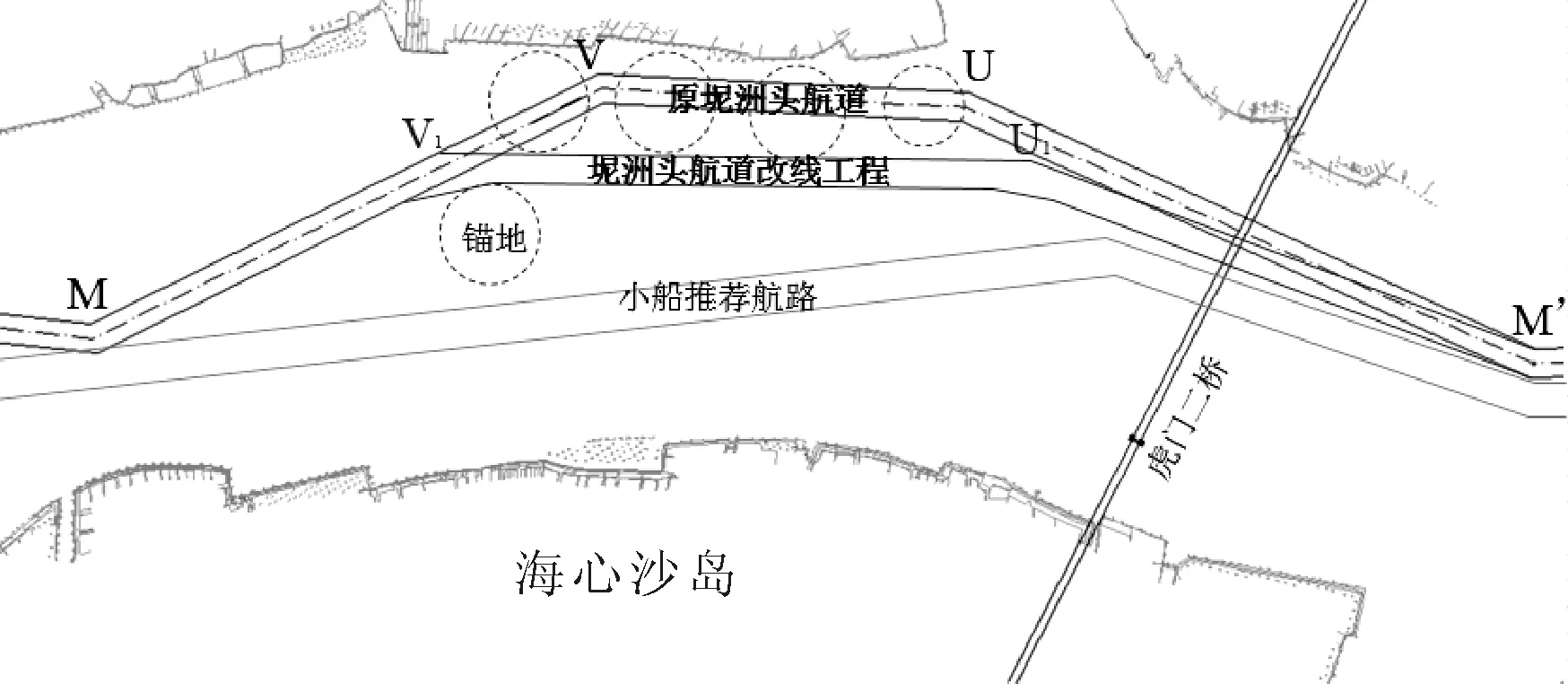
图1　坭洲头航道改线工程平面布置图

航道改线是一个复杂的工程，对于广东坭洲头航道而言，由于航道改线后，航道轴向发生变化，同时航道的平面布置也发生变化，这会导致各种通航参数对航道的影响状态也发生变化。其中，一部分通航参数得到改善，另一部分通航参数却有所恶化。改线前后航道通航参数对比如表1所示。

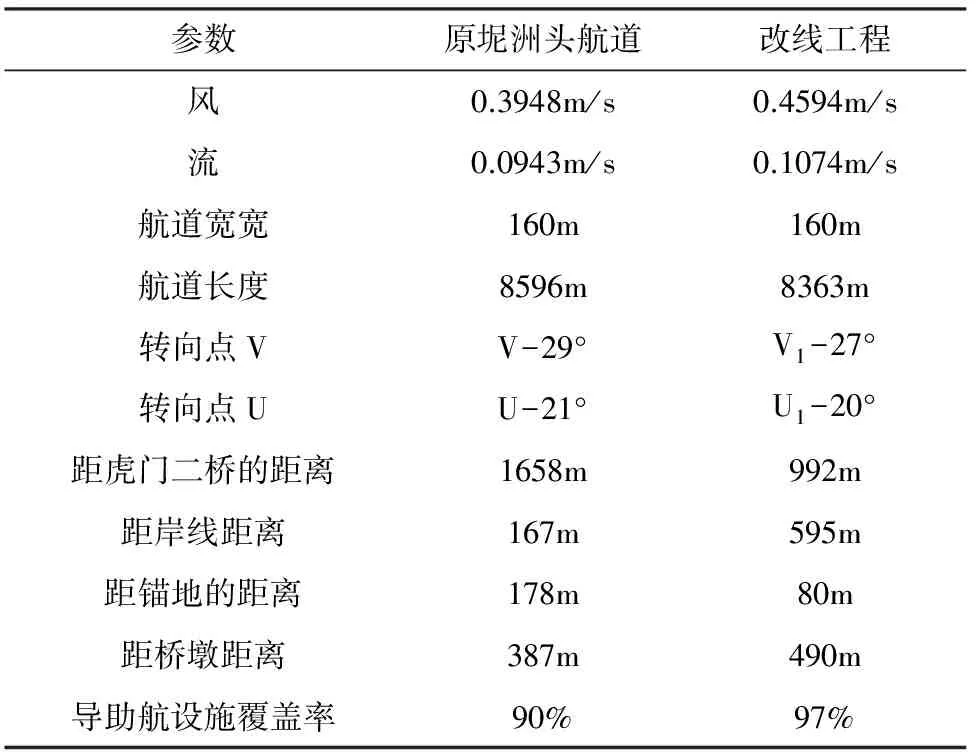
表1　坭洲头航道改线前后通航参数分析表

1.2　航道通航特征

广东坭洲头航道改线工程作为广州港出海航道的一部分，其通航特征比较复杂。为了全面掌握广东坭洲头航道改线工程的通航特征，结合相关研究成果，采用专家咨询和实地调研两种方法对广东坭洲头航道改线工程通航特征进行研究分析。通过研究分析广东坭洲头航道改线工程实际通航情况，总结出改线后航道的通航特征。目前，广东坭洲头航道改线工程实际通航特征主要包括以下四个方面：

(1)坭洲头航道改线工程与沿岸泊位的旋回圈较近，两者基本处于相切的位置关系。通常情况下，航道边线与旋回圈过近时，会给航道内正常航行的船舶以及靠离泊的船舶带来不利影响，制约船舶操纵，影响航道通航安全。同时，航道改线后，转向角设置有所改善，但是对于大型船舶来说改线后的转向角度仍然较大，给航道通航带来隐患。

(2)坭洲头航道改线工程位于出海口附近，受海洋性气候影响，自然环境条件复杂，易受风、流和大雾的影响。船舶在航道内航行时，受风、流影响将改变船舶受力情况，严重时会造成碰撞、沉没等事故。此外，在雾季来临时，航道内的能见度将显著下降，影响船舶驾驶人员的了望和操纵，增加通航风险。

(3)目前，我国航运业发展迅速，尤其是对于广州港这种国际性港口，船舶往返较多，导致进出港航道内的船舶密集。此外，根据该航道内的资料统计分析，船舶的尺度也逐年增大。因此，这一系列因素增加了航道内通航的复杂性和危险性，影响航道通航安全。

(4)由于坭洲头航道改线工程临近虎门二桥及一条过江电缆，虎门二桥的布置会影响在该航道内正常航行的船舶，增加附近水域的通航环境的复杂性和危险性，同时会对船舶的自由航行空间产生限制，增大操纵人员的工作压力，很容易诱发通航事故。

2　坭洲头航道改线前后通航风险评价研究

2.1　构建灰色模糊评价模型

航道通航风险评价系统是一个复杂的系统，对于航道通航风险研究来说，存在很多影响因素，同时各个因素之间也存在一定的相互影响，对通航风险的评价存在很大的模糊性；此外由于相关数据不充分，很难用经典的数学统计进行分析航道通航风险。因此本文结合两者的优势，构建出灰色模糊评价模型，其模型结构如图2所示。

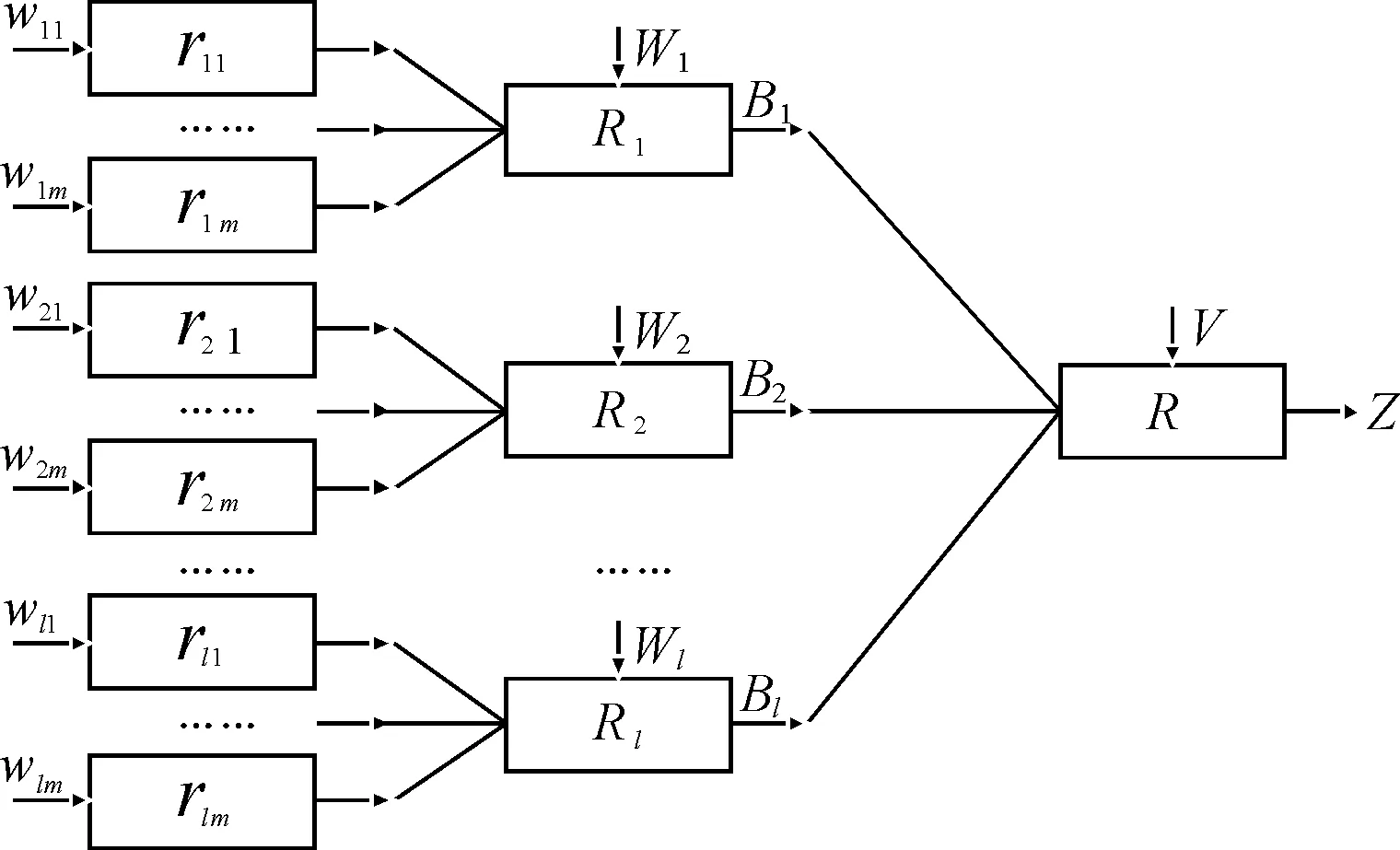
图2　灰色模糊评价模型

结合上述灰色模糊评价模型计算流程图，建立航道通航风险评价模型，模型构建步骤如下：

2.1.1构建样本矩阵

根据确定的航道通航风险评价指标体系，构建出航道通航风险评价模型。对于评价指标C，利用灰色模糊评价法对其进行安全评价，设一级评价指标的集合为C={C1，C2，…,Ci，…,Cs}(s为一级评价指标个数)，其中i=1，2，…，s；二级评价指标的集合为Ci={Ci1，Ci2，…，Cij，…，Cit}(t为二级评价指标中属于一级评价指标Ci的个数)，其中j=1，2，…，t。

n个专家按照标准分别对二级评价指标集合Ci={Ci1,Ci2,…,Cij,…,Cit}中的各个评价指标进行评分，即dijk(k=1,2,…，n)，利用dijk建立评价样本矩阵：

2.1.2建立白化权函数

通过综合研究航道通航的特征，将航道通航环境风险评价灰类分为5个等级，其中各个评价灰类的等级1、2、3、4、5依次对应危险、较危险、一般、较安全、安全。同时根据灰类确定各个灰类所对应的阀值，见表2。

表2　各个灰类对应的阀值

基于评价灰类和所对应的阀值，建立的白化权函数为[57-60]

(1)

(2)

(3)

(4)

(5)

2.1.3构建二级灰色模糊评价矩阵

根据各个专家对二级评价指标Cij的评分结果dijk，计算其在第e个评价灰类中的评价系数，记作：

(6)

二级评价指标Cij在各个评价灰类中的评价系数总和，记作：

(7)

计算各个灰类的评价系数，然后对其进行归一化处理，可得到灰色评价权值，记作：

(8)

统计评价指标Ci中的各个灰色评价权值，建立二级灰色模糊评价矩阵ri：

2.1.4计算一级指标评价结果

计算一级评价指标评价结果时，可将二级评价指标的各个权重Wi=(wi1,wi2,…,wij,…,wit)分别与对应的二级灰色模糊评价矩阵ri相乘，可得到对应的一级指标的评价结果，即Ri=Wiri。

2.1.5计算综合评价结果

利用一级指标Ci的评价结果的计算方法，求取总目标C的最终评价结果R，即R=Wr。根据最大隶属度原则，取C的评价结果R中的最大值，其所对应的灰类即为综合评价结果。

2.2　坭洲头航道改线工程通航风险评价

根据坭洲头航道改线工程通航风险评价指标体系，确定各级评价指标的集合(详见表3)，分别为：C={C1，C2，C3}，C1={C11，C12，C13}，C2={C21，C22，C23，C24，C25，C26},C3={C31，C32，C33}。

表3　坭洲头航道改线工程通航风险评价指标体系

针对坭洲头航道改线工程通航环境的特征，为了获得准确的评价结果，邀请相关通航安全领域的专家对各个评价指标进行打分。为了保障打分的精确性，规定评判区间为[0,10]，以方便各位专家根据自身的认知更加精确地评判各个评价指标的权重。同时根据每个专家的客观情况确定出每个专家的具体权重，进一步减少主观因素的影响。本文利用层次分析法对专家的权重进行设定，确定出各类专家权重分别为Q=(0.20,0.15,0.25,0.30,0.10)。根据每类专家的权重，对其进行均值处理，得到具体某一专家的权重。

根据集值统计法[5-8]计算出自然环境、航道条件、交通环境3个一级指标的相对权重:

并对相对权重进行归一化处理，确定出3个一级指标的最终权重:

W=(0.277,0.521,0.202)。

同理，可求出指标体系中各类二级指标的权重。各类二级指标权重计算结果分别为：

W1=(0.242,0.468,0.290)；

W2=(0.167,0.202,0.151,0.130,0.182,0.168)；

W3=(0.280,0.404,0.316)。

为了判断确定的权重是否合理，需对所求取的指标权重进行检验。根据区间方差法对指标权重进行可靠性性检验，其中F=(0.263,0.132,0.127)。检验结果表明，交通环境指标权重的可靠性相对较高，自然环境指标相对较低。

在计算出指标权重的基础上，利用评价模型对航道通航风险进行计算分析。邀请专家对二级指标进行打分，建立打分标准，打分范围为[0,10]。结合坭洲头航道改线工程的实际情况，各位专家分别对评价指标进行打分，统计指标得分情况。基于以上研究成果，对风险进行研究，通航风险评价分析步骤如下(具体步骤可参考文献[1])：

2.2.1确定评价灰类中的评价系数

对于二级指标C11，e=1时

y111=f1(d111)+f1(d112)+…+f1(d11n)

=37.136

同理，e=2时，y112=47.766；e=3时，y113=66.880；e=4时，y114=77.950；e=5时，y115=60.614。进一步计算出每一个评价灰类所对应的评价系数，并对其进行归一化计算，计算出灰色评价权向量为

r11=(0.128,0.165,0.230,0.268,0.209)

同理，计算C12和C13的灰色评价权向量，分别为

r12=(0.074,0.139,0.210,0.350,0.227)

r13=(0.081,0.104,0.146,0.243,0.426)

2.2.2确定灰色模糊评价矩阵

根据求取的灰色评价向量，建立的灰色模糊评价矩阵为

同理，根据上述方法，求取其他一级评价指标的灰色模糊评价矩阵，分别为

2.2.3确定一级指标评价结果

根据一级指标评价结果的方法，可得到一级评价指标的评价结果Ri=Wiri，分别为

R1=(0.089,0.135,0.196,0.299,0.280)

R2=(0.128,0.174,0.239,0.254,0.198)

R3=(0.116,0.145,0.208,0.261,0.267)

2.2.4确定航道通航风险综合评价结果

根据一级指标的评价结果Ri，建立广东坭洲头航道改线工程通航风险综合灰色模糊评价矩阵

根据一级指标的评价结果，建立综合灰色模糊评价矩阵。按计算一级指标评价结果的方法，可得到航道最终评价结果

R=Wr=(0.115,0.157,0.221,0.273,0.234)

广东坭洲头航道改线工程的综合评价结果中最大值为β4=0.273，根据模糊理论中最大隶属度原则，得到的评价结果所属灰类等级为4，因此改线后坭洲头航道通航环境的状况为较安全。

2.3　原坭洲头航道通航风险评价

为了研究坭洲头航道改线后通航条件是否有所改善，有必要对原坭洲头航道通航风险进行评价研究。通过研究原坭洲头航道的通航风险，可以看出航道改线前后通航条件的变化，同时验证改线是否科学、合理。

按照上述方法实现对原坭洲头航道的通航风险评价。由于评价对象都是坭洲头航道，因此可以利用同一评价指标体系，具体指标的权重也保持不变，各指标权重如下：

W=(0.277,0.521,0.202)

W1=(0.242,0.468,0.290)

W2=(0.167,0.202,0.151,0.130,0.182,0.168)

W3=(0.280,0.404,0.316)

然后，根据指标分值，计算出原坭洲头航道中各个灰色评价权向量，建立相应的评价矩阵，建立的评价矩阵分别为：

基于构建的评价矩阵，利用公式Ri=Wiri，可计算出原坭洲头航道评价指标体系中一级指标的评价结果。根据评价结果，构建出的相应评价矩阵为

则，可计算出原坭洲头航道通航风险为

R′=Wr′=(0.167,0.193,0.251,0.206,0.183)

从评价结果中可以看出，原坭洲头航道通航风险的综合评价结果为0.251，根据模糊理论中最大隶属度原则，得到的评价结果所属灰类等级为3，因此原坭洲头航道通航环境的状况为一般。

根据评价模型计算出改线后和原航道的最终评价结果，并对评价结果进行分析。结果表明，改线后航道内部分通航参数有所恶化，但在整体上航道通航安全情况得到大大改善，航道改线是合理的，同时评价结果也显示出改线后的航道，整体风险较低，处于可控的范畴。

3　航道通航风险评价软件设计与实现

为减轻风险评价的工作量，提高工作效率，提高评价结果的准确性，本文将会在评价模型理论研究分析的基础上，利用Microsoft Visual Studio 2010完成“航道通航风险评价软件”的设计编写。根据开发出的航道通航风险评价软件，以广东坭洲头航道改线工程通航系统为研究对象，针对坭洲头航道改线工程通航的具体特征，应用其进行实例分析。

根据开发出的航道通航风险评价软件，进行实例分析和验证。航道通航风险评价软件为广东坭洲头航道改线工程通航风险评价提供了很大的方便，大大减少了评估的工作量，提高工作效率。同时航道通航风险评价软件利用集值统计和灰色模糊理论作为理论基础，减少主观因素对整体评价结果的影响。

3.1　解析指标模型

根据所构建的指标体系，导入航道通航风险评价软件。由于航道通航风险评价软件中编写了执行逻辑，系统会自动按照执行逻辑，直接解析出评价指标模型，录入航道通航风险评价软件系统。

3.2　导入数据信息

结合专家最终的打分情况和专家自身的权重，统计原始数据，建立评价指标分值数据库，直接在软件中导入数据信息。导入数据信息时，应分析和对比数据，检查数据的准确性，避免错误信息导入系统从而影响评价结果计算的准确性。

3.3　指标权重计算

在航道通航风险评价软件导入坭洲头航道改线工程通航风险特征的原始数据信息后，在主界面中点击计算结果窗口，软件会根据原始数据信息直接显示二级指标权重的数值，同时利用鼠标可读取一级指标的具体数值。用户还可以利用鼠标读取指标权重确定的可靠性。指标权重计算结果如图3所示。

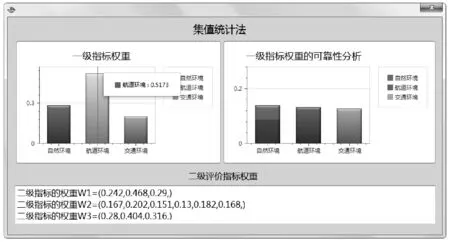
图3　坭洲头航道改线工程通航风险 评价指标体系权重计算结果

指标权重计算结果的设计是基于集值统计法的思想，设计编写程序。集值统计相较传统的权重计算方法，其计算结果更加准确。由于集值统计不是具体的一个数值，而是一个区间，在一定程度上减少了主观因素的影响，保障指标权重计算的准确性、客观性。

3.4　综合评价结果计算

计算综合评价结果的时候，需要建立评价灰类，根据评价灰类构建白化权函数，然后利用白化权函数确定评价指标的隶属度。通过编写执行逻辑和数学算法，航道通航风险评价软件会基于集值统计法和灰色模糊理论，对相应数据进行分析处理后，得到综合评价结果。综合评价结果如图4所示。

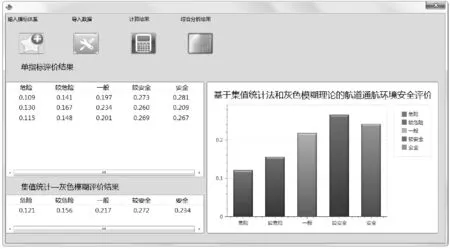
图4　坭洲头航道改线工程通航风险综合评价结果

根据航道通航风险评价软件运行计算，可知广东坭洲头航道改线工程通航风险的评价结果为R″=Wr=(0.121,0.156,0.217,0.272,0.234)。根据模糊理论中的最大隶属度原则，取综合评价结果中的最大值0.272，其所对应的评价灰类的等级是4，坭洲头航道改线工程通航风险的最终评价结果为较安全。

4　综合评价结果分析和量化

4.1　评价结果分析

在研究广东坭洲头航道改线工程通航风险时，用传统计算方法和软件运算分别得到两个评价结果，对计算的评价结果进行分析，其中两评价结果分别为

R=Wr=(0.115,0.157,0.221,0.273,0.234)

R″=Wr=(0.121,0.156,0.217,0.272,0.234)

对比两评价结果发现，两者基本一致，表明航道通航风险评价软件的设计具有适用性、可行性。同时将坭洲头航道改线工程通航风险综合评价结果与航道的实际情况相比，基本吻合，表明软件的设计具有一定的实际工程应用价值。

4.2　评价结果量化

为了将定性的评价结果进行定量化，根据航道通航风险评价软件计算出的综合评价结果，对每个评价灰类分别进行赋值，进而得到航道通航风险评价结果所对应的各个评价灰类量化向量是

U=(60,70,80,90,100)

即，航道通航风险评价结果值Z=RUT=83.42。

因此可知，坭洲头航道改线工程通航风险的评价结果为较安全，如果以满分为100分作为衡量标准来看，该航道的最终得分为83.42分。坭洲头航道改线工程整体通航风险可控，坭洲头航道改线工程是合理的。

5　结语

本文通过利用构建的灰色模糊评价模型，对广州坭洲头航道改线工程通航风险进行客观评价，评价结果可信。同时，为减少传统方法计算的工作量，本文利用集值统计和灰色模糊理论为理论基础，开发设计出航道通航风险评价软件，软件可为广东坭洲头航道改线工程通航风险评价提供了很大的方便，大大减少了评估的工作量，提高工作效率。

通过实例验证分析，将航道通航风险评价软件应用在广东坭洲头航道改线工程通航风险的评价上，根据航道实际设计数据的输入，计算出的通航风险大小与实际情况差别不大，取得了理想、可信的评价结果，基本上可以满足航道通航风险评价的要求。通过对评价结果进行分析和定量化处理，可以直观的反映出广东坭洲头航道改线工程通航风险的实际大小，为航道管理部门提供参考和依据。

[1]贾明明,熊锡龙,等.基于集值统计——灰色模糊的航道通航环境安全评价[J].安全与环境工程,2017,17(1):41-45.

[2]徐磊.集对-粗糙集综合安全评估方法在港口航道通航安全中的应用[D].大连:大连海事大学,2013.

[3]吴建军.分道通航制水域航行环境安全的集对综合评价研究[D].大连:大连海事大学,2010.

[4]王方金.航道通航风险评估模型的研究[D].大连:大连海事大学,2012.

[5]方宏伟,李长洪,纪洪广,等.基于粗糙商集的模糊隶属度集值统计算法[J].北京科技大学学报,2012,34(8):959-965.

[6]Kiyoshi Hara, Shiny Nakamure.A Comprehensive assessment system for the Maritime traffic environment[J].Safety science, 1995,19(2-3):203-215.

[7]Rojas C A M, Alvan R M, Carrasco-Olivera D. Topological entropy for set-valued maps[J]. Discrete and Continuous Dynamical Systems-Series B, 2017,20(10):3461-3474.

[8]Yu G L. Topological properties of Henig globally efficient solutions of set-valued problems[J]. Numerical Algebra Control & Optimization, 2017,4(4):309-316.

[9]Foata, Dominique, Han, et al. New permutation coding and equidistribution of set-valued statistics[J]. Theoretical Computer Science, 2009,410(38):3743-3750.

[11]张靖岩,臧桂丛,李引擎,等.基于模糊数学与集值统计的既有建筑火灾危险性评估模型[J].安全与环境工程,2012,19(5):82-84.