金属材料低温冲击试验不确定度的评定

薛　欢　刘　念　熊　飞

(宝钢股份中央研究院武汉分院(武钢有限技术中心)　湖北　武汉：430080)

1　不确定度简介

近年来，测量结果评定标准的混乱、评定方法精确度的争论使得各个科研院所、企业实验室之间的测量数据无法进行有针对性的比较。传统的“误差”概念针对的是测量精度，其无法获得对被测量的真值，仅是一种近似反映。为了规避“误差”表示测量数据可能引起的问题，许多专家、国际组织提出了利用“测量不确定度”来代替传统误差表征体系，对测量数据的精度进行正确评定[1-2]。

A类标准不确定度是指用对观测列的统计分析进行评定得出的标准不确定度，B类标准不确定度是指用不同于对观测列的统计分析来评定的标准不确定度。“A”类和“B”类不确定度，并没有本质上的区别。A类不确定度是由试验结果数据中观测得到的频率分布导出的概率密度函数得出，B类不确定度则考虑的是对试验这个事件发生的信任度(常称主观概率或先验概率)[3]。两者都基于概率的分布，都可以用方差或标准差来表示。A、B类不确定度不存在哪一类更为可靠的问题。近年来，国际学者们均认为，为规避混淆与误解可能性，不再使用“系统不确定度”和“随机不确定度”这两个术语。在需要区分不确定度性质时，一般用“由于随机效应导致的不确定度分量”及“由于系统效应导致的不确定度分量”这两种表达方式。其并不说明不确定度是由哪种方法得到的。换言之，由系统效应引出的不确定度分量既可以用A类方法，同时也可以用B类评定方法评定[4-7]。不确定度的评定方法和其性质之间没有绝对的对应关系。

2　金属材料低温冲击试验不确定度的计算

由于试验涉及干扰项较多，金属材料的低温冲击试验检测结果的影响因素复杂。例如试样尺寸、加工精度，缺口加工状态、冲击试验机的刚度、摆锤、刀刃形态、回零差、底座跨距、曲率半径及斜度等都对试验结果有影响。而试验条件中的冲击速度、试样对中性以及温度均匀性、时效等、试样材质的不均匀性和各试验人员的差别等也会影响试验数据的可靠性。如果按照国家计量技术规范《测量不确定度评定与表示》中的直接法对金属材料试样进行低温冲击试验检测结果进行测量不确定度评定，那么需要根据冲击试验的数学模型，对各环节所引入的不确定度分量进行评定，再按不确定度传播规律进行合成、扩展。这其中有一些输入量很难准确界定，还有一些重要因数无法考虑进去。例如材料的不均匀性、试样加工的允许偏差及试样对中、温度均匀性、时效性等差别等，这些不确定因素引起的不确定度均很难准确用单独的数学方式计算。这样得出数据的准确性及可靠性都不高[8]。

采用综合法可以提高低温冲击试验结果测量不确定度评定的准确性和可靠性。综合法是综合考虑并评定试验结果重复性(包括操作、材料均匀性、试样尺寸、试验控制、温度差异等影响)、试验仪器误差、标准试样的标准偏差、数据修约等因素所引入的不确定度分量，而后再进行合成、扩展，最后得出不确定度结果。该方法不仅增强了冲击试验检测结果不确定度评定的可操作性，还提高了检测数据测量不确定度评定的可靠性和准确度。不仅是冲击试验，对于其它很难用直接评定法进行不确定度评定的测试，都可以采用综合进行评定。

在测试方法、试验仪器、试样及标准试样均满足试验标准GB/T229-2007的前提下，试验试样的冲击吸收功测量结果不确定度的主要来源为四个：(1)测量重复性引起的不确定度u1(此分量中包含了试样材料不均匀性、试验人员、试样加工及试验条件的差别等影响因素)；(2)工作仪器误差所引入的不确定度分量u2;(3)标样的标准偏差所引入的不确定度分量u3;(4)测量数据的数值修约所引入的不确定度分量u4。

2.1　试验结果重复性所引入的不确定度分量

由于试样材料均匀性、试样加工、不同人或同一人员多次操作、试验机本身的重复性等因素都必然存在着差异，其引入的不确定度分量u1采用A类方法进行评定。在本评定中，由冲击操作岗位上的3位试验人员，每人进行1组试验，每组10个试样。试样为55mm*10mm*10mm V型缺口标准试样。对于船用耐蚀钢-20℃冲击试验和桥梁用钢-40℃冲击试验评定数据分别见表1和表2。

试验数据标准偏差Si由贝塞尔公式计算：

(1)

(2)

标准差的平均值为：

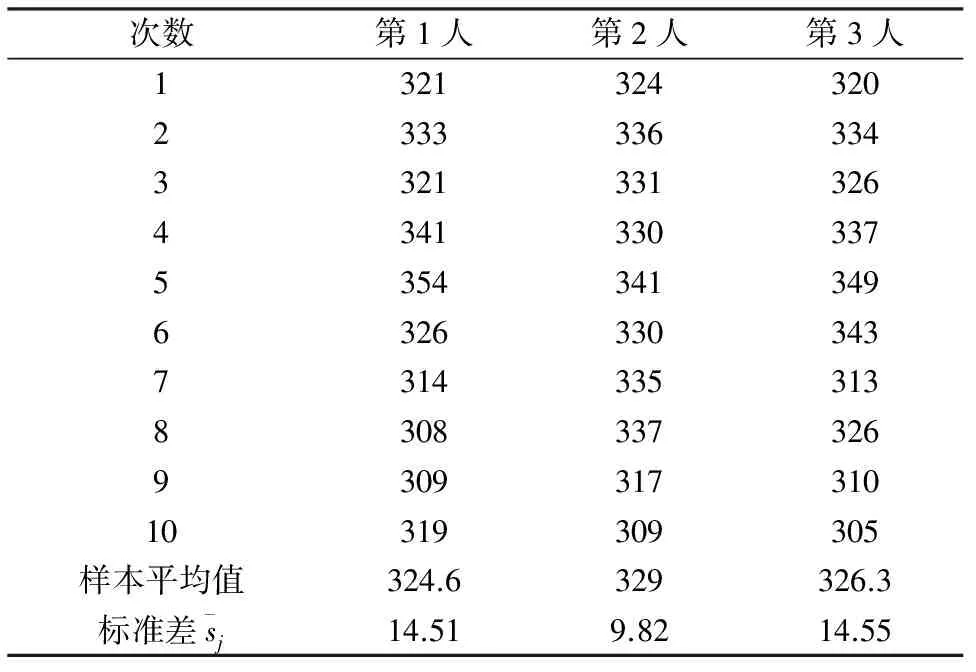
表1　船用耐蚀钢-20℃冲击试验重复性评定数据(单位：J)

(3)

标准差的标准差为：

(4)

所以试验状态是稳定的，可以应用高可靠性的合并样本标准差Sp。在实际试验中，对于正常的任一次冲击试验，每次冲击一个试样得到一个试验数据(k=1)，因此该分量为：

u1rel(x)= 13.15/(324.6+329+326.3)/3

=4.03%

(5)

同上文所述可以计算出合并标本标准差为：15.39J；标准差的平均值为：15.31J；标准差的标准差为：1.94J。而标准差的标准差

(6)

说明检测状态也是稳定的，可以应用高可靠性的合并样本标准差Sp。在实际试验工作中，每次冲击一个试样只得到一个数据(k=1)，那么该不确定度分量为：

u1rel(x)=7.9%

(7)

2.2　工作试验机误差所引入的不确定度分量u2

各实验室用于冲击测试工作的试验机，即工作试验机必须要按照国家标准GB/T3808—2002进行检验。首先需要进行各个项目的直接检验，通过后，还需要利用标准试样进行间接检验，并达到标准规定的各项要求。工作试验机重复性所引入的不确定度已包含在上述所求出的分量之中。而试验机本身的最大允许误差E满足：当能量A<40J时，E=±4J；当能量AR≥40J时，E=±10%AR。AR为标准试样组的能量值。对于超高冲击值的UH级，本试验机AR=240J。当AR≥40J时，误差的半宽是10%AR，服从均匀分布，则：

(8)

2.3　标准试样标准偏差所引入的不确定度分量u3

根据国家标准GB/T 18658，标准试样允许的标准偏差S满足：当能量AR<40J时，S≤2J；当能量AR≥40J时，S≤%5AR。标准试样标准偏差所引入的不确定度分量u3满足t分布：

(9)

其中S为标准试样组的标准偏差；n为标准试样组的标样个数；tp为t分布在置信概率p时的tp值。根据国家标准GB/T 18658中对标准冲击试样的要求，将25个或更多标准试样测得的能量值的平均值作为该批的标准能量值，同时计算标准偏差S。对于此评定，最小的自由度是v=n-1=25-1=24。置信概率取为68%，查表得到

tp(v)=t68(24)=1.02

当AR≥40J时，

1.02×0.05×240/5=2.45(J)

(10)

而本实验室实际情况是该级别标准试样试验只有5个试样，此时tp(v)=t68(4)=1.14

(11)

比标准规定值大了2倍有余，值得重视。

2.4　根据标准对测量结果数值修约所引入的不确定度分量u4

对于数字修约，修约间隔为δx，则所引入的不确定度分量为u4(x)=0.29δx。当A<10J时，修约间隔为0.1；J当A>10J时，修约间隔为1J。

因此，当A<10J时，u4(x)=0.29δx=0.029J；J当A>10J时，u4(x)=0.29δx=0.29J。 可见此项比前3项小1个数量级，因此在合成不确定度时，忽略不计。

2.5　相对合成不确定度

(12)

船用耐蚀钢-20℃冲击试验

桥梁用钢-40℃冲击试验

2.6　相对扩展不确定度

扩展不确定度等于包含因子与合成标准不确定度的乘积，在置信概率取95%时，k=2。

Urel(x)=k·ucrel(x)

(13)

船用耐蚀钢-20℃冲击试验

Urel(x)=k·ucrel(x)=2×6.14%=12.28%

桥梁用钢-40℃冲击试验

Urel(x)=k·ucrel(x)=2×11.08%=22.16%

2.7　各不确定度分量之间的对比

船用耐蚀钢-20℃冲击试验及桥梁用钢-40℃冲击试验各不确定度分量见表3所示。其中测量重复性及试验机误差所占比重分别为43%和48%，以及51%和41%，为该试验的主要影响因素，标准样品的标准偏差占比为9%和8%为次要影响因素，而修约因素基本可忽略不计。

表3　不确定度分量对比

3　结论

进行了金属材料冲击试验不确定度分量研究：测量重复性引起的不确定度u1，此分量中包含了试样材质的不均匀性、人员操作、试样加工及试验条件的差异等因素；试验机误差所引入的不确定度分量u2;标准试样标准偏差所引入的不确定度分量u3;测量结果数值修约所引入的不确定度分量u4。进行了船用耐蚀钢-20℃冲击试验和桥梁用钢-40℃冲击试验的不确定度评定，其扩展不确定度分别为12.28%和22.16%。相对而言，其中测量重复性及试验机误差所占比重较大，而数值修约所引入的不确定度分量基本可忽略不计。

[1]粱晋文,陈林才,何贡.误差理论与数据处理 [M].北京：中国计量出版社，2003．

[2]上海计量测试技术研究院.常用测量不确定度评定方法及应用实例[M].北京：中国计量出版社，2001．

[3]BIPM,IEC,LFCC,ISO,IUPAC,IUPAP,OIML.Guide to the expression of uncertainty in Measurement. Corrected and Reprinted GUM[M].Geneve Switerland:ISO,1995.

[4]JJF 1059-1999.测量不确定度评定与表示[S].

[5]王承忠.测量不确定度与误差的区别及在评定中应注意的几个问题[J].冶金分析,2004,24:678-682.

[6]刘岑,杨帆,吴元祥.钢材拉伸试验数据同质性的判别[J].武汉工程职业技术学院学报,2017,29(2):17-19.

[7]薛欢.桥梁用钢拉伸试验不确定度的评定[J].武汉工程职业技术学院学报,2017,29(1):11-14.

[8]王承忠.测量不确定度直接评定法和综合评定法的几个典型实例[M].理化检验-物理分册,2006,42:320-323.